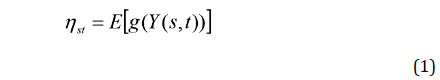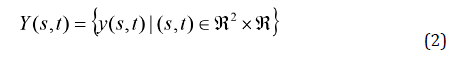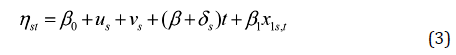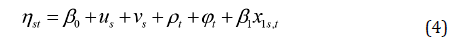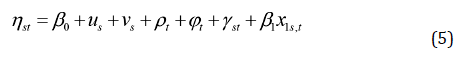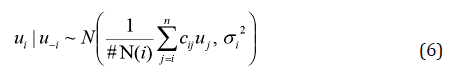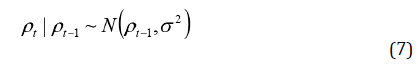1. Introducción
La enfermedad por COVID-19 (WHO, 2020a) inició a finales de 2019 con el reporte de casos atípicos de neumonía en la ciudad de Wuham, China (WHO, 2020b). Se trata de una enfermedad respiratoria causada por el virus SARS-CoV-2 que ha producido a nivel mundial más de 300 millones de casos y causado más de 5 millones de muertes al 14 de enero de 2022 (Worldometer, 2022). La OMS definió una situación de pandemia el 11 de marzo de 2020 (WHO, 2020c) y en sus inicios se calculó una tasa reproductiva de la enfermedad de 2.6 (Imai, et al., 2020). Con ese parámetro, la fracción de población que potencialmente se afectará sin el establecimiento de medidas de mitigación es de 60% (Anderson et al, 2020). Sin embargo, dicho parámetro está sujeto a variaciones geoFiguras, socio-demoFiguras y de capacidad evolutiva del virus (Namasivayam, et al., 2021; Sebastião, et al., 2021; Phan, 2020; Liu et al., 2020; Liu et al., 2021). Existe, además, una correlación no aleatoria entre los factores de exposición y la incidencia de COVID-19, por lo que es importante mejorar la comprensión de los determinantes asociados a la transmisión del virus, más allá de los factores de riesgo epidemiológicos y clínicos (China CDC Weekly, 2020; Wu et al., 2020; Zhou et al., 2020). Los efectos en la salud por la propagación del COVID-19 han tenido una distribución desigual entre poblaciones, espacios geográficos y a lo largo del tiempo (Alm et al., 2020; Sharma et al., 2020; Hall et al., 2021), por lo que el análisis de las desigualdades en salud (Marmot et al., 2020) resulta fundamental para la definición en el largo plazo de estrategias enfocadas a proteger a las poblaciones con mayor grado de vulnerabilidad.
En México se reportaron los primeros casos de COVID-19 el 29 de febrero de 2020 (WHO, 2020d) y para el 14 de enero de 2022 se habían acumulado más de 4 millones de casos y 300 mil muertes (Woldometer, 2022). El comportamiento epidemiológico de la pandemia en México ha sido similar a lo descrito para China (Suárez et al., 2020), incluyendo una distribución geográfica heterogénea en su incidencia (Fernández-Rojas et al., 2021). Existen, sin embargo, determinantes sociales que se expresan en una mayor exposición a la enfermedad, como son la movilidad por razones económicas, los niveles de hacinamiento poblacional (Hernández-Flores et al., 2020), la pertenencia a algún grupo étnico o a población indígena (Ramírez-Aldana et al., 2021).
Un estudio sobre salud de los pueblos indígenas en México mostraba que el perfil de patologías que presentaban era propio de poblaciones en condiciones de pobreza y marginación social (Sepúlveda et al., 1993). A 26 años de su publicación, la población indígena en México continúa presentando la misma situación de pobreza y vulnerabilidad. La Encuesta Nacional de Salud y Nutrición 2018-2019 muestra que la población indígena sin instrucción escolar fue de 16.6%, en contraste con 6.2% para la población no indígena; el nivel socioeconómico en el primer quintil fue de 60.3% vs. 15.6%; acceso a servicios del Instituto Mexicano del Seguro Social, 20.7% vs. 44.5%; y hogares en zona rural, 51.5% vs. 19.7%, respectivamente (Pelcastre-Villafuerte et al., 2020).
El presente trabajo sustenta la hipótesis de que la tasa de incidencia de COVID-19 ha afectado en mayor medida a las poblaciones indígenas, en especial a las poblaciones que se encuentran espacialmente hacinadas. Se evalúa la evolución espacio-temporal de las tasas de morbilidad por COVID-19 considerando el efecto que la presencia de población indígena residente en los diferentes municipios del país ejerce sobre la incidencia de contagios por COVID-19, con base en los casos reportados entre los meses de febrero de 2020 y octubre de 2021.
2. Metodología
Los datos sobre casos de COVID-19 registrados en México fueron obtenidos de la Dirección de Información del Sistema de Vigilancia Epidemiológica de la Secretaría de Salud de México (Secretaría de Salud, 2020) y se recuperaron desde el inicio de la pandemia hasta el 31 de octubre de 2021. Los datos sobre la población residente a mitad de año en los municipios, fue recopilada de las Proyecciones de Población de los Municipios de México 2015-2030 bases 1 y 2, elaboradas por el Consejo Nacional de Población (Partida & García, 2018), mientras que el porcentaje de población hablante de lengua indígena por municipio fue tomado del Censo General de Población y Vivienda 2020, disponible en la página del INEGI. Es importante señalar que, si bien a partir del segundo semestre de 2021 se consolidó la vacunación contra el COVID-19 en México, no se cuenta con información a nivel municipal que permita integrar el efecto de la misma a la evolución espacio-temporal de la incidencia entre la población indígena y la población general.
2.1 Plan de análisis
Desde un enfoque histórico y sociocultural, la población indígena ha sido definida como:
aquellos grupos descendientes directos de los pueblos que habitaban América desde antes de la llegada de los españoles en el siglo XV, que poseen una lengua y cultura propias y que comparten formas de vida y cosmovisiones particulares, diferenciadas de las occidentales (Bello & Rangel, 2002, p. 40).
Sin embargo, el criterio establecido por el INEGI para definir a las poblaciones indígenas en México es el lingüístico. Así, la población indígena se conforma por aquellas personas de tres o más años que afirman hablar alguna lengua indígena. Por su parte, los datos colectados por el Sistema de Vigilancia Epidemiológica en México identifican los casos positivos como aquellos cuyo resultado de una prueba de laboratorio sea positivo o que se clasifiquen positivos por asociación epidemiológica o por dictamen (en caso de defunción). De esta forma, se calcula la tasa de incidencia de COVID-19 como el cociente del número de casos positivos entre la población residente en el municipio a mitad del año por cada mil habitantes, y se estima el porcentaje de población indígena como el cociente de la población hablante de lengua indígena de tres años o más residente en el municipio dividido por la población residente en el municipio con tres años o más de edad.
Según cifras de INEGI al 2020, 5.8% de la población de México es indígena, en tanto que las cifras de contagios por COVID-19 registrados a nivel nacional alcanzaron los 3 811 793 personas, de las cuales 39 429 eran indígenas autoadscritos y 24 572 eran población indígena (hablante de lengua indígena), cifras al 31 de octubre de 2021. Lo anterior implica que 3.02% de la población general y 0.53% de la población indígena se han contagiado de COVID-19. La diferencia en el número de contagios para ambos grupos poblacionales puede verse a lo largo del tiempo en las Figuras 1(a) y 1(b), donde se presentan los casos de COVID-19 entre los meses de febrero de 2020 a octubre de 2021.
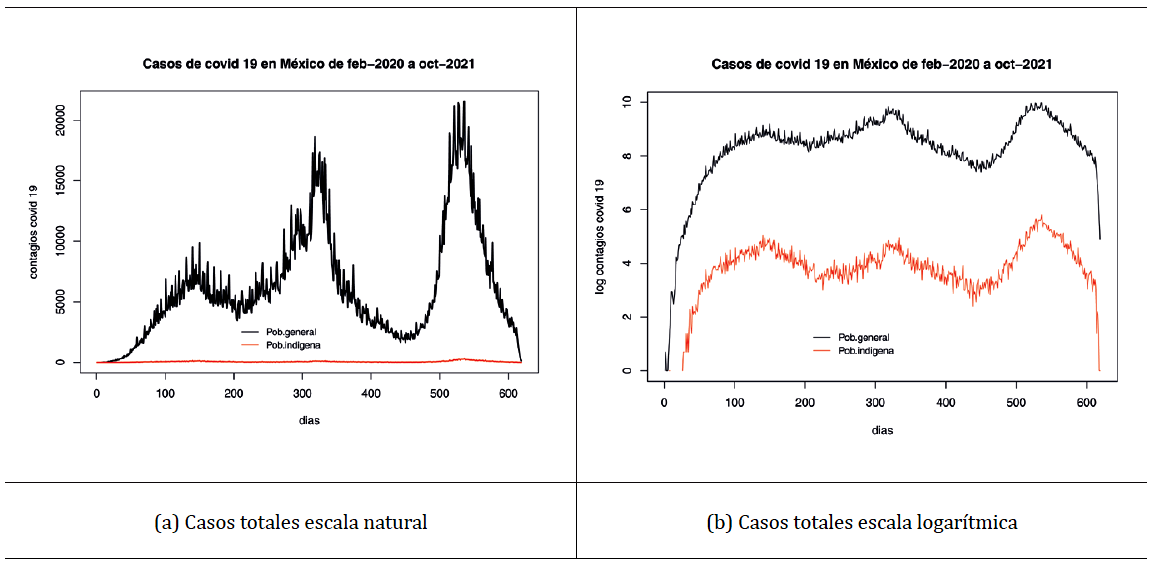
Fuente: elaboración propia con datos de la Secretaría de Salud y Consejo Nacional de Población (CONAPO, febrero de 2020 a octubre de 2021).
Figura 1. Serie de tiempo de los casos totales de COVID-19 en México
Las Figuras 1(a) y 1(b) presentan la serie de tiempo de los casos totales registrados de infección por COVID-19 en México al 31 de octubre 2021, presentando la distribución en escala natural y logarítmica y estratificando por población general e indígena. La Figura 1(a) hace evidente el elevado nivel de subregistro de casos de COVID-19 para poblaciones indígenas. Mientras que la Figura 1(b) muestra que, pese al elevado nivel de subregistro de casos, el comportamiento seguido por la pandemia en ambas poblaciones es el mismo. Es decir, se trata de un problema de nivel y no de tendencia, dado que no se observa un comportamiento atípico de la pandemia para el caso de la población indígena. Sin embargo, la Figura 1(b) permite identificar la presencia de un importante nivel de subregistro, asociado a la ausencia de casos de COVID-19 en poblaciones indígenas, dado que no existe ninguna evidencia científica que permita justificar un comportamiento atípico en dichas poblaciones, pero tampoco se cuenta con alguna otra estadística que permita corregir adecuadamente el subregistro observado, razón por la que se trabaja con los datos presentados.
El trabajo se centra en analizar la relación que existe entre la presencia de población indígena en un municipio y la incidencia de casos de COVID-19 en el mismo. Por esta razón, se omite el uso de covariables que pudieran generar algún efecto de correlación, como pudiera ser el acceso a servicios de salud o educación, bienes y servicios al interior de la vivienda, ingresos o tipo de empleo. Así, se aísla el efecto espacial que ejerce la proporción existente de personas hablantes de lengua indígena sobre la incidencia de COVID-19 en los municipios de México, para el periodo analizado. Asimismo, se excluye a la población que se autoadscribe como indígena, debido a que consideramos que el ser hablante de alguna lengua indígena permite capturar de forma más eficiente lo que conlleva ser indígena en términos socioculturales y permite, por tanto, capturar el efecto generado por el COVID-19 sobre dicha población.
El problema de subregistro observado a nivel nacional presenta también marcadas diferencias a nivel estatal y municipal, tal y como puede verse en la Figura 2. En esta, como se ha señalado, la tasa de incidencia de COVID-19 a nivel nacional es de 30.2 por mil habitantes; y la ciudad de México alcanza una tasa de 105.5 por mil vs. Chiapas, que tiene una tasa de 4.2 contagios por cada mil habitantes. En general, las entidades federativas con mayores porcentajes de población indígena presentan menores tasa de incidencia de COVID-19, con excepción del estado de Yucatán, donde destaca el municipio de Benito Juárez (Cancún).
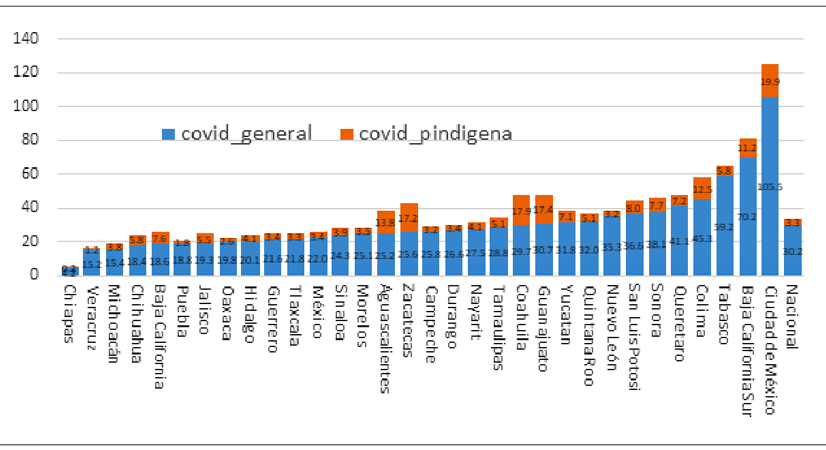
Fuente: elaboración propia con datos de la Secretaría de Salud y CONAPO.
Figura 2. Tasa de COVID-19 por entidad federativa, México 2020-2021
A continuación, se presentan tres modelos espaciales en competencia que tienen como finalidad evaluar el efecto que la presencia de población indígena ejerce sobre la distribución espacial de la incidencia de COVID-19 en los municipios de México para los meses de febrero de 2020 a octubre de 2021.
2.2 Modelación espacio-temporal bayesiana
Los modelos espacio-temporales bayesianos son un caso particular de los modelos gaussianos latentes. Donde la variable aleatoria a modelar y(s,t) sigue una distribución perteneciente a la familia exponencial con media μs,t = g -1 (ηs,t), de modo que el predictor lineal ηs,t del modelo espacio-temporal se define en términos del valor esperado de la función de enlace de la variable a modelar:
Donde y(s,t) representa la tasa de incidencia de COVID-19 en el municipio s al mes t (Blangiardo & Cameletti, 2015) y a la vez y(s,t) define un proceso estocástico como una sucesión indexada:
En el que la variable y(s,t) sigue una distribución normal con media μs,t. Por lo que el modelo espacio-temporal en su formulación clásica paramétrica se define como:
El modelo espacio-temporal en su forma dinámica no paramétrica se define como:
Y el modelo de interacción espacio-temporal se especifica a partir de
En el modelo clásico paramétrico, tanto el efecto temporal global (β) como la tendencia espacial diferencial (δs) se ven limitados por una estructura lineal (Bivand et al., 2015), mientras que en los modelos no paramétricos y de interacción espacio-temporal las tendencias espacio-temporales se ajustan a partir de una combinación dinámica de efectos estructurados y no estructurados.
En los modelos presentados en las ecuaciones (3), (4) y (5), el término β 0 representa la tasa media de incidencia de COVID-19 en los municipios de México para el periodo estudiado, ui representa el efecto espacial estructurado, v s el efecto espacial no estructurado y β 1 el efecto asociado a la covariable x 1s,t (porcentaje de población indígena).
El componente espacial estructurado (u i ) sigue una distribución condicional definida por:
Donde el criterio de vecindad c ij toma el valor de c ij = 1 si las áreas i y j son vecinas, en otro caso c sij = 0. La varianza σ 2 i = σ2 u /#N(i) se define en función de la cantidad de vecinos N (s) , y del área s (Rue et al., 2009). El componente espacial no estructurado v s se distribuye como una Normal (0, σ v 2 ) con varianza σ v 2 que captura la dispersión de los efectos espaciales no estructurados (Riebler et al., 2016).
En el modelo clásico paramétrico cada unidad espacial tiene una tendencia temporal dada por el intercepto (β 0 +u s +v s ) y por la pendiente (β+δ s ) (Blangiardo & Cameletti, 2015), mientras que en los modelos no paramétrico y de interacción espacio-temporal la tendencia temporal estructurada ρt es modelada de manera dinámica a través de una caminata aleatoria de orden uno (rw(1)) dada por:
Y la tendencia temporal no estructurada φt se modela utilizando una distribución previa gaussiana intercambiable N(0, 1/τφ) (Schrödle & Held, 2011). El parámetro de interacción espacio-temporal definido para el modelo (5) sigue una distribución gaussiana γ st ~ Normal (0, 1⁄τ γ ) (Sharafifi et al., 2018). En general, los modelos espacio-temporales suponen que el predictor lineal se integra como la suma de términos espaciales y temporales separables, por lo que la matriz de covarianza presenta una estructura que permite separarla como el producto de dos matrices: una matriz de efectos espaciales y una de efectos temporales (Martino & Rue, 2008).
3. Resultados
La estimación de los modelos se realizó utilizando el método Integrated Nested Laplace Approximation (INLA), implementado en el paquete R-INLA (Rue et al., 2009), disponible en lenguaje de programación R (R Core Team, 2016), el cual se presenta como una alternativa computacionalmente eficiente respecto de métodos tradicionales como el MCMC (Gamerman & Lopes, 2006).
Debido a que se propusieron tres modelos diferentes para estimar el comportamiento espacio-temporal de un mismo fenómeno, resulta necesario definir una serie de criterios que permitan identificar al modelo que represente la mejor alternativa. Para esto se suelen emplear criterios de calidad de ajuste de modelos, en nuestro caso se utiliza el criterio de información de Akaike (AIC) que permite ponderar entre la complejidad del modelo y su calidad de ajuste de los datos. El criterio AIC elige el modelo que alcanza el menor valor del estadístico. Los resultados de la estimación del AIC para los modelos (3), (4) y (5) se presentan en la Tabla 1 e indican que debe seleccionarse el modelo (5) de interacción espacio-temporal.
Tabla 1. Criterio de información Akaike, diferentes modelos

Fuente: elaboración propia con base en estimaciones de R-INLA.
La Tabla 2 presenta las estimaciones posteriores para los parámetros que corresponden a los efectos fijos de los tres modelos propuestos que incluyen la estimación de la media, desviación estándar, y primero, segundo y tercer cuartil. En contraparte, la Tabla 3 presenta las estimaciones para los efectos espaciales y temporales tanto de efectos estructurados como no estructurados para el modelo de interacción espacio-temporal, mientras que las Figuras 3 y 4 presentan la distribución espacio-temporal del logaritmo natural de la tasa de incidencia de COVID-19 observada y de la tasa ajustada por el predictor lineal del modelo de interacción espacio-temporal para los municipios de México.
Tabla 2. Estimación posterior de efectos fijos de los modelos (3), (4) y (5)
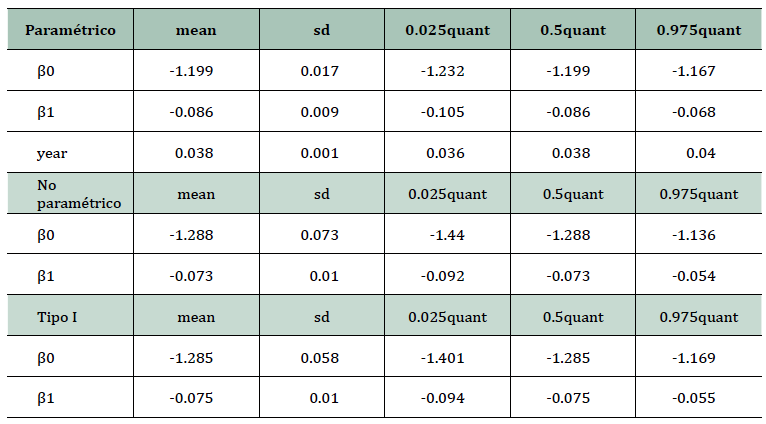
Fuente: elaboración propia con base en estimaciones de R-INLA.
Tabla 3. Estimación posterior de efectos fijos de los modelos (3), (4) y (5)
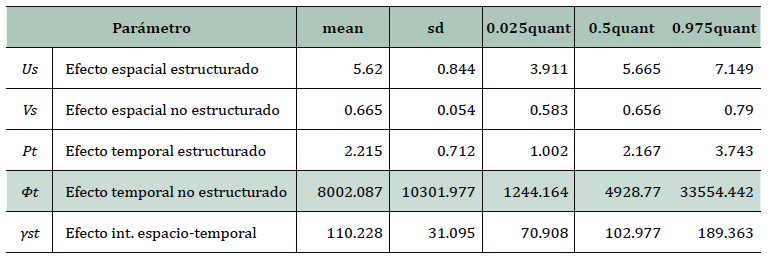
Fuente: elaboración propia con base en estimaciones de R-INLA.
Fuente: elaboración propia con base en estimaciones de R-INLA.
Figura 3. Tasa de incidencia observada de COVID-19
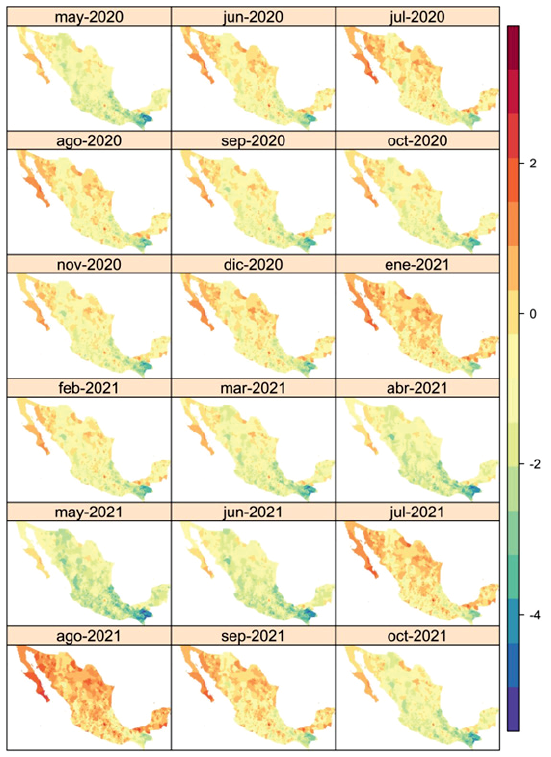
Fuente: elaboración propia con base en estimaciones de R-INLA.
Figura 4. Tasa de incidencia estimada de COVID-19, modelo de interacción tipo I
Es importante señalar que tanto las tasas de incidencia de COVID-19 como las proporciones de población indígena se ingresaron a los modelos en escala logarítmica con la finalidad de reducir posibles sesgos derivados de la sobrevariabilidad presente en los datos, de manera que antes de interpretar los parámetros estimados se debe aplicar la función exponencial.
Así, la estimación posterior del parámetro β 0 correspondiente al modelo (5) muestra un valor de exp(-1.285) = 0.276 (véase Tabla 2), lo que implica una subestimación de la tasa de incidencia de COVID-19 para el periodo estudiado, la cual, como se mostró anteriormente, es del orden de 30.2 contagios. En tanto que β 1 = exp(-0.075) = 0.927 puede interpretarse como el efecto que el incremento de un punto porcentual de población indígena ejercería sobre la tasa de incidencia de COVID-19, en este caso significa que el aumento de un punto de población indígena provocaría un incremento de 0.9 puntos de incidencia de COVID-19, es decir que tiene un efecto protector de 0.1 puntos porcentuales (ver Tabla 2).
La Tabla 3 presenta el valor medio, desviación estándar y cuartiles estimados para los efectos espaciales, temporales y de interacción espacio-temporal del modelo (5). En particular, se observa la estimación del parámetro de efectos temporales no estructurados φt = 8002.08, que alcanza un valor mucho mayor al estimado por el resto de los efectos espaciales y temporales, lo que indica que la evolución temporal del COVID-19 en los municipios de México fluctúa de manera importante en razón de variaciones temporales aleatorias, por lo que depende en menor medida de los efectos estructurados. Es decir, asigna un menor peso relativo a las variaciones derivadas de efectos estructurados espaciales u s = 5.6 y temporales ρt = 2.2, asociados a la estructura de vecindades y al calendario, respectivamente.
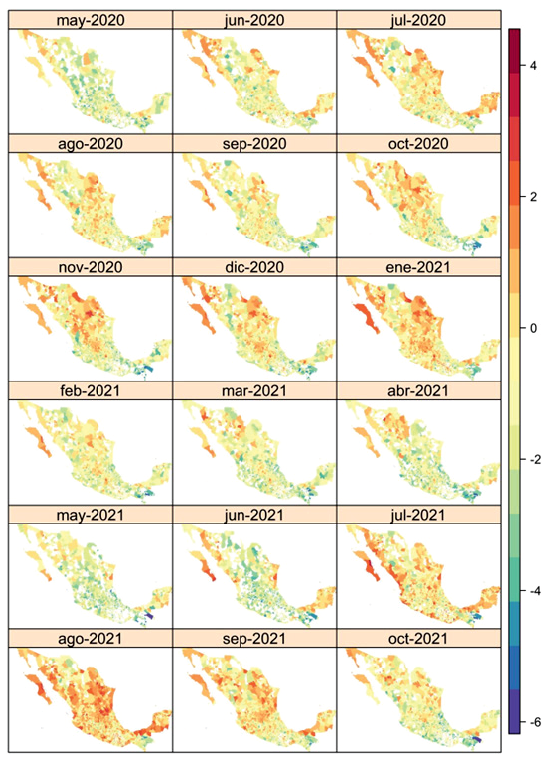
La distribución espacio-temporal de la tasa de incidencia de COVID-19 en los municipios de México se muestra en la Figura 3 1. En general, se observa una tendencia oscilatoria en relación al número de municipios afectados en función de las tres olas de contagios registradas en México hasta octubre de 2021, lo que implica la presencia de un pico de contagios en el mes de julio de 202 correspondiente a la primera ola, así como dos picos más en los meses de enero y agosto de 2021 (véase Figura 4), cuando se registraron los máximos de la segunda y tercera ola, respectivamente. Se debe enfatizar que la modelización y análisis comprende el periodo de febrero de 2020 a octubre de 2021, y que las variaciones espaciales y temporales observadas en la Figura 3 corresponden al logaritmo natural de las tasas de incidencia de COVID-19 observadas, mismas que se presentan con fines de comparación con respecto de las estimaciones realizadas por el modelo (5) presentadas en la Figura 4.
La Figura 4 presenta la media posterior estimada por el modelo de interacción espacio-temporal del logaritmo natural de la tasa de incidencia de COVID-19, de manera que las tasas estimadas pueden ser contrastadas directamente con las tasas crudas presentadas en la Figura 3. En la Figura 4 puede observarse un sobreajuste de las tasas de incidencia de COVID-19 para algunos municipios del norte de México, en especial para los meses de julio de 2020 y enero, agosto y septiembre de 2021, a la par puede observarse en la Figura 3 cómo el modelo (5) estima correctamente el valor medio esperado de las tasas de COVID-19 en los municipios donde no se cuenta con información sobre casos registrados o en municipios donde no se registraron casos; sin embargo, podría presentarse también un efecto de sobreajuste para tales estimaciones.
La Figura 5 presenta la tendencia de los efectos temporales estructurados ρt y no estructurados φt estimada por el modelo de interacción espacio-temporal (5). En la misma se observa un comportamiento casi constante del efecto temporal estructurado, alrededor del 1, es decir, los cambios producto de variaciones aleatorias capturados por los efectos temporales estructurados generan variaciones relativamente menores a las generadas por cambios en el calendario; en contraparte, el efecto temporal estructurado captura los picos correspondientes a las tres olas de contagios por COVID-19 registradas en México cuyos máximos se presentaron en los meses de julio de 2020 y enero y agosto de 2021. En la misma Figura 5, se observa cómo el efecto temporal no estructurado se mantiene alrededor de la unidad y en todo momento por debajo del efecto estructurado, con dos excepciones: los primeros tres meses de la pandemia y el mes de mayo de 2021, lo que implica que el efecto de las variaciones temporales no estructuradas generadas por variaciones temporales aleatorias tiene una incidencia relativa menor sobre la evolución de los contagios de COVID-19 que los efectos producto de cambios en el calendario.
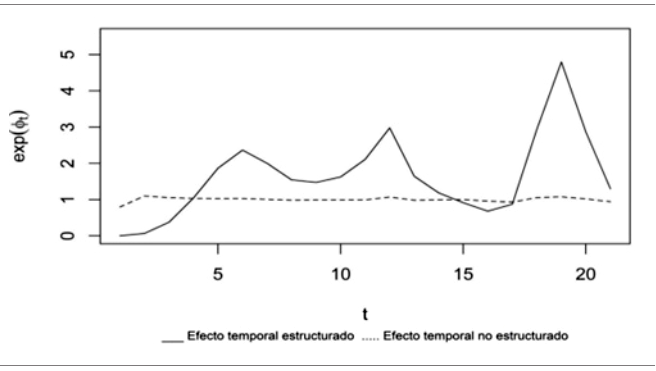
Fuente: elaboración propia con base en estimaciones de R-INLA.
Figura 5. Efectos temporales estructurados y no estructurados modelo de interacción espacio-temporal tipo I
Las tasas de incidencia de COVID-19 presentadas en la Figura 4 indican que los efectos espaciales son relativamente menos importantes que los efectos temporales, por lo que se sospecha que la evolución de los contagios tiene un fuerte componente asociado a variaciones temporales, las cuales fueron capturadas mayormente por el efecto temporal no estructurado, mismo que puede verse en la Figura 5. El efecto temporal no estructurado presenta una tendencia casi constante alrededor del 1 (cuando es de esperarse que los errores aleatorios se concentren alrededor del 0), en el sentido que las variaciones temporales no capturadas por la estructura del calendario generan efectos constantes sobre la evolución de casos de COVID-19, efectos que posteriormente se dispersarían a lo largo del espacio.
4. Discusión
Los resultados de este estudio mostraron que la tasa de incidencia de infección por COVID-19 en la población general fue 5.6 veces mayor que la encontrada en la población de habla indígena, lo que muestra la presencia de un efecto protector para esta última. No solo el estimador puntual de infección difiere entre la población general y la indígena, también la tendencia de los casos en el tiempo lo mostró, en particular las curvas logarítmicas describen el mismo patrón de distribución de los casos a lo largo del periodo estudiado en las dos poblaciones, aunque la magnitud de casos de la población indígena fue menor. Estos resultados son opuestos a lo propuesto en la hipótesis de trabajo, lo que sugiere que existen diferentes circunstancias sociales que pueden tener un «efecto protector» en la población de habla indígena.
Los resultados anteriores son consistentes con los del análisis espacio-temporal bayesiano de la incidencia de COVID-19 en los municipios de México. La estimación posterior de los efectos fijos del modelo para el parámetro β1, correspondiente a la población de habla indígena, fue de 0.9 (exponencial del logaritmo -0.075) que, como es menor a la unidad, muestra que se tiene un efecto protector de la infección por COVID-19 con respecto al efecto promedio del área estudiada. Asimismo, el análisis del modelo de interacción de los efectos medios temporales, espaciales y espacio-temporales de la incidencia de COVID-19, mostraron que la mayor magnitud se encontró en el efecto temporal no estructurado, lo que indica que la dinámica de la transmisión del COVID-19 estuvo relacionada con las variaciones aleatorias de la infección ocurridas a lo largo del tiempo.
Las tasas de incidencia de COVID-19 tuvieron un alto grado de heterogeneidad entre municipios, con fluctuaciones simultáneas en el espacio-tiempo. Si bien se observan municipios con bajas tasas de incidencia de COVID-19, existen otros con tasas positivas que, en términos de la tasa reproductiva de la infección, son municipios con mayor densidad poblacional y por tanto con mayores niveles de interacción entre personas. Al mismo tiempo, se presentaron cambios en las tasas de infección a lo largo del tiempo que correspondieron a los picos epidémicos que se presentaron en México en el periodo de estudio, el primero entre julio y agosto de 2020, el segundo entre enero y febrero de 2021, y el tercero entre agosto y septiembre de 2021 (Worldometer, 2022).
Resulta interesante observar que las tasas de incidencia estimadas de COVID-19 relativas a la población de habla indígena son bajas en los municipios de los estados donde las magnitudes de dicha población son altas y donde se concentra el 68% de su totalidad, principalmente en los estados de Oaxaca, Chiapas, Veracruz, Puebla, Yucatán y Guerrero (INEGI, 2020), situados en el sur y sureste de México. En la Figura 4 se puede observar que gran parte de los municipios en estos estados presentaron tasas de infección negativas o alrededor del valor de nulidad, incluso durante el primer y el segundo pico de la epidemia. Esta se extendió a gran parte de los municipios en el territorio mexicano durante el tercer pico de la epidemia en agosto de 2021, pero llama la atención que la región de Chiapas, en la Selva Lacandona y sus alrededores, se mantuvieron con valores negativos en las tasas de la infección. La Figura 2 muestra que, entre los estados con menor frecuencia de infección por COVID-19 en población de habla indígena, están precisamente Chiapas, Veracruz, Puebla, Oaxaca y Guerrero, que concentran 59.8% del total de dicha población.
Estos resultados sugieren que la transmisión del COVID-19 en la población en México no es aleatoria, sino relacionada con diferentes circunstancias sociales. La primera circunstancia se refiere a que proporciones significativas de población de habla indígena vive en comunidades de baja densidad poblacional. La mitad de esta población vive en comunidades menores a 2500 habitantes y un quinto de esa población vive en comunidades menores a 15 000 habitantes (CONEVAL, 2019). La baja densidad poblacional estaría relacionada con una baja tasa de transmisión del virus, a diferencia de lo que se ha planteado a nivel mundial, en que la infección por COVID-19 se ha extendido rápidamente debido a una alta interconectividad internacional, creciente urbanización y alta concentración demográfica (Sigler et al., 2021; Wong & Li, 2020). En México se ha encontrado que la densidad poblacional alta tiene gran impacto en la transmisión del virus (Hernández-Flores et al., 2020). En ese sentido, se ha mostrado que la tasa de contagio por COVID-19, definida como el número de contagios por 10 000 habitantes, fue mayor en los municipios urbanos (mayores a 100 000 habitantes) en promedio un 54.4 por ciento mayor, seguida de una frecuencia media en los municipios semiurbanos (entre 20 000 y 99 999 habitantes) de 24.9, y la menor frecuencia se presentó en los municipios no urbanos (menos de 20 000 habitantes) de 15.7 (Hernández Bringas, 2020).
La segunda circunstancia que explicaría la existencia de un efecto protector de la infección por el COVID-19 en población de habla indígena es el subregistro de casos. La población indígena se encuentra en México con un rezago social que tiene raíces históricas que aún tienen expresión en la actualidad. Por ejemplo, en relación con las poblaciones de menos de 1500 habitantes y de 10 000 habitantes para el año 2018, la carencia de seguridad social fue de 61.5% y 78%, y la carencia de acceso a servicios de salud fue de 19.6% y 16.2%, respectivamente (CONEVAL, 2019). Estas cifras denotan un acceso limitado de la población de habla indígena a los servicios de salud, lo que se refleja incluso en el número de pruebas para detectar COVID-19. Hernández Bringas (2020) muestra que la tasa de contagio por COVID-19 depende del número de pruebas realizadas. Así, las pruebas por 100 000 habitantes fueron, para los municipios de nivel urbano, semiurbano y no urbano, de 1153, 500 y 345, respectivamente. Aunque las tasas de contagio por 10 000 habitantes fueron de 24.9 y 15.7 para los municipios semiurbanos y no urbanos, donde se encuentra la mayor parte de población de habla indígena, la tasa de contagio para esta población fue de 34.1, lo que denota una mayor susceptibilidad de la población indígena a la infección por COVID-19.
La tercera circunstancia se refiere a la definición que se haga de población indígena para diferenciarla de la no indígena. Así, las diferentes formulaciones de las preguntas censales, como las que incluyen la condición étnica de «cultura» versus la condición autoadscrita como indígena, pueden tener efectos de sobrestimación o subestimación del volumen de la población indígena (Vázquez Sandrin & Quezada, 2010). Otra forma de definir a la población indígena es el de preguntar por el habla de una lengua indígena. Esta es la definición que Hernández Bringas (2020) utilizó para su estudio y la que hemos utilizado en este trabajo.
5. Limitaciones
Si bien el estudio concluye que la tasa de incidencia de infección por COVID-19 en la población indígena es significativamente menor al encontrado en la población general, es importante resaltar que los resultados se encuentran sujetos a errores derivados del subregistro de casos presentados en comunidades indígenas, producto de la carencia de acceso a servicios médicos, de un adecuado sistema de registro para comunidades indígenas en casos de COVID-19, el uso de medicina tradicional y su elevado nivel de aislamiento geográfico respecto de los principales centros poblacionales.
Adicionalmente, la aproximación anidada integrada de Laplace (INLA) es una alternativa rápida y eficiente a métodos tradicionales como la cadena de Markov Monte Carlo (MCMC) para la inferencia bayesiana, aunque INLA presenta algunas limitaciones, entre las que destacan: (1) el método está diseñado para aplicarse a modelos gaussianos latentes, por lo que no puede manejar directamente distribuciones no gaussianas, lo que implica un ajuste inadecuado cuando no se cumple dicho criterio. (2) En general, el método presenta dificultades de ajuste cuando el número de efectos aleatorios e hiperparámetros se incrementa, es decir que los modelos complejos suelen presentar problemas de convergencia y (3) las predicciones pueden subestimar la verdadera incertidumbre, dado que existen menos diagnósticos disponibles para INLA en comparación con MCMC, e INLA carece de las garantías de convergencia asintótica teórica que posee MCMC, por lo que resulta complicado su uso para la elaboración de proyecciones.
6. Conclusiones
Se puede concluir que el modelo de análisis espacio-temporal bayesiano tiene la capacidad de capturar la compleja dinámica de la transmisión del COVID-19 en términos de la estructura de dependencia proveniente de tres fuentes de variación: (1) la variación en el espacio, (2) la variación en el tiempo y (3) la variación conjunta espacio-temporal. Tiene, además, la capacidad de incluir covariables, como x1 que representó el porcentaje de la población indígena. Se trata de una herramienta analítica de gran utilidad para cuantificar el efecto que ejerce el porcentaje de población indígena sobre la evolución de la epidemia de COVID-19 en los municipios de México, que en este caso resultó ser un efecto protector, es decir, el habitar en un municipio con una elevada proporción de población indígena reduce el riesgo de infección por COVID-19. Sin embargo, este resultado debe leerse con cautela debido al elevado nivel de subregistro de casos presentado al inicio de este trabajo. Subregistro que puede evidentemente invalidar los resultados expuestos. No obstante, el trabajo permite orientar decisiones en política pública para el control de la pandemia por COVID-19, no solo porque corrobora los resultados obtenidos a través de la estadística paramétrica clásica, sino porque modela la dinámica de la transmisión espacio-temporal del COVID-19, tanto para la población indígena como para la población general.
Finalmente, los patrones de distribución espacio-temporal de la incidencia de COVID-19 estimados para los municipios de México presentados en las Figuras 3 y 4 permiten identificar la formación de conglomerados espacio-temporales con altas y bajas tasa de incidencia. En particular, los patrones observados hacen evidente la presencia de desigualdades en salud, diferencias sustentadas en términos de la proporción de población indígena residente en los municipios. Asimismo, el uso de modelos bayesianos deriva de su capacidad para integrar información previa del fenómeno a través de un proceso que añade nueva evidencia, lo que le permite obtener estimaciones confiables.