1. INTRODUCCIÓN
En este artículo se presenta un estudio sobre la evaluación de un agitador recíproco utilizando tecnología Arduino y un sistema de control PID ajustado por el método de Ziegler-Nichols. La investigación se centra en mejorar el rendimiento del equipo, garantizar una agitación precisa y constante, y explorar la viabilidad de integrar prácticas de economía circular en el proceso de fabricación. Además, se evalúan las ventajas de esta metodología en comparación con los métodos tradicionales, destacando la precisión del control de velocidad y la estabilidad bajo diferentes condiciones de carga. Este estudio busca proporcionar un enfoque sostenible y accesible para la fabricación de equipos de laboratorio.
2. ANTECEDENTES
La pandemia de COVID-19 ha generado un cambio radical en la educación global, impulsando una rápida adopción de la enseñanza virtual y el aprendizaje autodirigido. En este nuevo paradigma educativo, la construcción y optimización de equipos por parte de los propios estudiantes ha emergido como una estrategia esencial para desarrollar la creatividad, el pensamiento crítico y las habilidades prácticas [1]. No obstante, para que estos equipos sean verdaderamente efectivos en entornos educativos y de investigación, es crucial que ofrezcan un rendimiento y funcionalidad comparables a los equipos comerciales estándar [2]. Esta necesidad no solo desafía a los educadores y estudiantes a innovar, sino que también abre la puerta a enfoques sostenibles como la economía circular, donde la reutilización y mejora de componentes desempeñan un papel central en la creación de soluciones de laboratorio asequibles y eficientes [3], [4], [5] y [6].
El avance de la tecnología de hardware abierto, como Arduino, ha democratizado el acceso a la creación de equipos de laboratorio asequibles y altamente funcionales, impulsando la innovación en diversas disciplinas científicas [7]. En este marco, el presente trabajo se enfoca en la evaluación y optimización de un agitador recíproco antiguo, optimizado mediante un sistema de control PID basado en el método de Ziegler-Nichols. La implementación de este sistema de lazo cerrado permite corregir errores de velocidad y garantizar una agitación precisa y controlada.
La agitación mecánica es un proceso fundamental en muchas aplicaciones científicas, especialmente en la dispersión de partículas y la preparación de muestras para análisis precisos. Los agitadores recíprocos han demostrado ser herramientas eficaces para realizar agitaciones controladas, garantizando la homogeneidad de las muestras, lo cual es esencial para obtener resultados confiables. El desempeño de los agitadores recíprocos ha sido evaluado en estudios previos, como el realizado por [8], donde se analizó su efectividad en la dispersión mecánica de muestras de suelo. Los resultados mostraron una alta precisión y repetibilidad en la dispersión de partículas, destacando las ventajas de estos dispositivos en términos de bajo costo y facilidad de uso. Además, investigaciones previas han subrayado la importancia de la agitación controlada en la estabilidad y precisión de los análisis, como se observa en los trabajos [9]. Aunque los estudios han demostrado la efectividad de los agitadores recíprocos en aplicaciones específicas [10], existe una falta de investigación que aborde la optimización de estos equipos mediante tecnologías modernas, como el control PID y la integración con sistemas de bajo costo como Arduino [11]. Este vacío en la literatura justifica la investigación actual, el objetivo de este estudio es optimizar el rendimiento de los agitadores recíprocos, lo que permitirá aumentar su eficiencia en experimentos científicos, facilitando su uso en entornos educativos y mejorando la calidad de la investigación en laboratorios. Esto también busca ampliar la aplicabilidad del equipo, haciéndolo más accesible y práctico para diversas actividades educativas y de investigación. La pregunta clave es: ¿Puede la optimización de un agitador recíproco mediante control PID y tecnología Arduino mejorar su rendimiento y precisión, integrando además prácticas de economía circular? Para responder a esto, se implementó un control PID ajustado con el método de Ziegler-Nichols, evaluando su desempeño en condiciones controladas. Este enfoque, documentado por su eficacia en la estabilización de sistemas mecánicos, también aborda preocupaciones económicas y ambientales al extender la vida útil de los equipos mediante la reutilización de materiales. Además de mejorar la funcionalidad, este trabajo promueve la economía circular y demuestra el potencial de la tecnología de hardware abierto en la creación de soluciones sostenibles y accesibles para la comunidad educativa y científica [12].
3. METODOLOGÍA
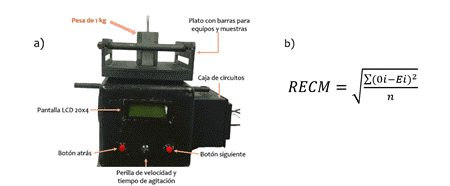
Se reutilizó un motor AC de 40 W, integrando un microcontrolador Arduino y un sensor óptico para lectura de velocidad (ver Fig. 1) Se evaluó el desempeño del equipo bajo diversas cargas, ajustando las constantes PID para optimizar la respuesta del sistema.
3.1 Método de control PID
El sistema de control implementado incluye un controlador PID, cuya función detallada se muestra en la Figura 1. Este controlador incorpora un filtro pasa bajo (LPF) diseñado para atenuar las señales de alta frecuencia en la componente derivativa, mejorando la estabilidad del sistema. Además, se utilizó una estrategia de control por sujeción para resolver el problema de anti “wind-up” en la componente integral del controlador, según lo descrito por [8]. Para mejorar la precisión de las mediciones, se añadió un filtro de Kalman al sensor óptico, lo que permite reducir significativamente el ruido en las señales del sensor, de acuerdo con la metodología de [13].
3.2 Prueba de control
La adquisición de las constantes proporcional (Kp), integral (Ki), y derivativa (Kd) (ver Tabla I) se llevó a cabo siguiendo el método de sintonización de Ziegler-Nichols. El procedimiento comenzó configurando el sistema como un controlador proporcional puro (tipo P), con Ki y Kd ajustados a cero. Posteriormente, la constante proporcional (Kp) se fue incrementando gradualmente hasta observar oscilaciones en la velocidad, momento en que se alcanzó el tiempo de asentamiento del sistema. A partir de ahí, Kp se continuó aumentando hasta que se detectaron las primeras oscilaciones estables, obteniendo así la constante crítica (Kc). Se probaron distintos valores de Kc, como Kc = {5, 5.5, 6, 6.5, 7}, registrándose los datos necesarios para determinar el período de oscilación (Pu) correspondiente a cada Kc, como se muestra en la Fig. 2.
Con los valores de Kc y Pu establecidos para cada condición, se aplicó la tabla de ajuste del método de Ziegler-Nichols para calcular las constantes Kp, Ki, y Kd óptimas, tal como se detalla en la Tabla I.
Dado que se implementó una estrategia anti wind-up para evitar la acumulación de error integral, se decidió fijar el valor de Ki en cero. En términos de programación, esto se tradujo en las siguientes expresiones: "aggKp = Kp", "aggKi = 0", "aggKd = Kd". Este enfoque simplificado facilita tanto la implementación como el ajuste de las constantes PID en condiciones específicas, asegurando una mayor estabilidad del sistema.
3.3 Prueba eléctrica con carga
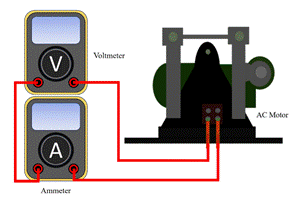
Para medir el consumo eléctrico de la máquina se conectó un multímetro en serie para medir la corriente de la fuente (que también circula por el motor) y otro en paralelo a las terminales del motor (o salida del regulador) para medir el voltaje, ver (Fig. 3). Se realizaron las mediciones de corriente y voltaje consumidos por el motor a velocidades de oscilación de 150, 200, 250 y 300 RPM, sometidos a pesos de 0, 0.25, 0.5, 1, 1.5, 2, 3 y 5 kg.
3.4 Prueba de error de rpm con carga
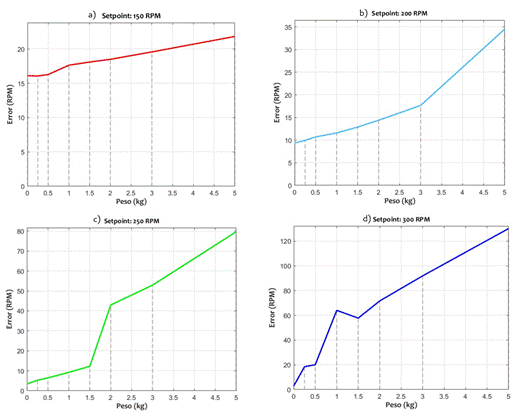
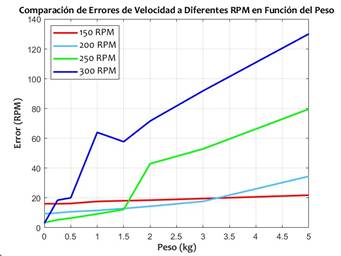
Se realizaron pruebas con diferentes pesos para definir un rango de peso específico para el funcionamiento óptimo del equipo. La prueba midió el error de medición en condiciones de 1 minuto a varias velocidades de punto de ajuste (150 RPM, 200 RPM, 250 RPM, 300 RPM) y con diferentes pesos (0 kg, 0,25 kg, 0,5 kg, 1 kg, 1,5 kg, 2 kg, 3 kg, 5 kg) ver (Fig. 4 y Tabla II).
La prueba consiste en agitar bajo condiciones de diferentes pesos y RPM durante 1 minuto. Se llevó a cabo con el propósito de delimitar un rango específico de RPM y peso donde la agitación tenga un bajo error de RPM.
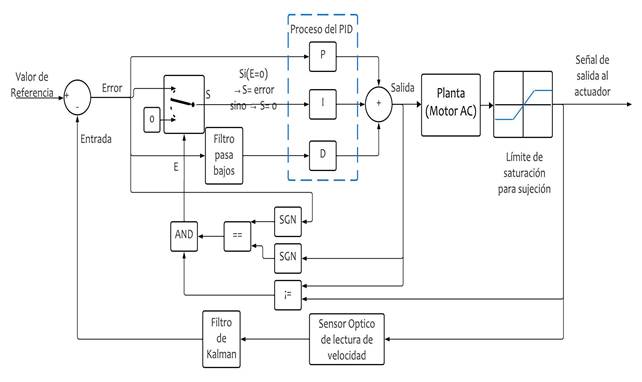
Fig. 1 Diagrama de bloques del controlador PID con LPF para la parte derivativa y anti “wind-up” para la parte integral [14] con adición a un filtro de Kalman para los sensores [15].
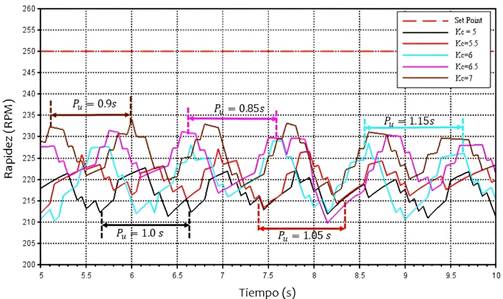
Fig. 2 Oscilación para cada caso de Kc, velocidad (RPM) versus tiempo (s), determinación del periodo Pu para la evaluación del ajuste de parámetros de control PID.
TABLA I Tabla de Sintonización de Ziegle Nichols
| Tipo de Controlador | Kp | Ki | Kd |
| P | 0.5Kc | - | - |
| PI | 0.5Kc | 2(Kp/Pu) | - |
| PID | 0.6Kc | 2(Kp/Pu) | 0.125PuKp |
TABLA II Tabla de errores con diferentes pesos a velocidades de 150, 200, 250 y 300 RPM
| Peso (kg) | Error(RPM) | |||
| 150 RPM | 200 RPM | 250 RPM | 300 RPM | |
| 0 | 16.11 | 9.36 | 3.42 | 2.97 |
| 0.25 | 16.07 | 9.95 | 5.27 | 18.48 |
| 0.5 | 16.28 | 10.70 | 6.46 | 20.08 |
| 1 | 17.64 | 11.58 | 9.21 | 64.02 |
| 1.5 | 18.10 | 12.90 | 12.25 | 57.75 |
| 2 | 18.50 | 14.39 | 42.96 | 71.63 |
| 3 | 19.58 | 17.67 | 52.92 | 91.89 |
| 5 | 21.83 | 34.51 | 79.69 | 130.14 |
4. ANÁLISIS DE RESULTADOS
4.1 Método de control PID
El sistema de lazo cerrado implementado permite corregir las discrepancias entre el valor deseado y la lectura del sensor que mide las revoluciones por minuto (RPM) en cada intervalo de tiempo. Este sistema envía órdenes al motor para mantener la velocidad deseada, compensando perturbaciones tales como cambios de masa, fuerzas externas o el desgaste del motor. El modelo de control adoptado es el PID, y su ajuste se realizó utilizando el segundo método de Ziegler-Nichols, una técnica ampliamente utilizada por su simplicidad y rapidez, que no requiere un conocimiento previo del modelo matemático del sistema, ideal para fines educativos [16] [17]. La Fig. 1 muestra la función detallada del controlador junto con el filtro pasa bajo (LPF) para atenuar las señales de alta frecuencia del controlador derivativo y la estrategia de control Clamping para resolver el problema de anti wind-up del controlador integral. Por último, se añadió un filtro de Kalman al sensor óptico para reducir el ruido en las mediciones, mejorando la precisión de las lecturas [15].
El sistema de lazo cerrado implementado permite corregir las discrepancias entre el valor deseado y la lectura del sensor que mide las revoluciones por minuto (RPM) en cada intervalo de tiempo. Este sistema envía órdenes al motor para mantener la velocidad deseada, compensando perturbaciones tales como cambios de masa, fuerzas externas o el desgaste del motor. El modelo de control adoptado es el PID, y su ajuste se realizó utilizando el segundo método de Ziegler-Nichols, una técnica ampliamente utilizada por su simplicidad y rapidez, que no requiere un conocimiento previo del modelo matemático del sistema, ideal para fines educativos [16] [17]. La Fig. 1 muestra la función detallada del controlador junto con el filtro pasa bajo (LPF) para atenuar las señales de alta frecuencia del controlador derivativo y la estrategia de control Clamping para resolver el problema de anti wind-up del controlador integral. Por último, se añadió un filtro de Kalman al sensor óptico para reducir el ruido en las mediciones, mejorando la precisión de las lecturas [15].
4.2 Prueba de control
La determinación de las constantes de control se describe en la sección de metodología, utilizando el proceso de ajuste de Ziegler-Nichols. Este método exige la generación de gráficos de oscilación para cada valor de la constante crítica, junto con su período correspondiente (ver Fig. 5). A partir de los valores obtenidos se a partir de la TABLA I, se construyó la TABLA III, en la que se evaluaron cinco configuraciones diferentes para calcular las constantes Kp, Ki y Kd.
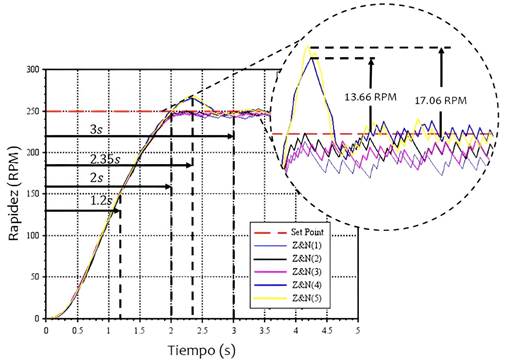
Los resultados mostraron que, para alcanzar un objetivo de 250 RPM, el tiempo promedio de estabilización fue de aproximadamente 3 s. Esto se traduce en un error porcentual del 3% considerando el sistema sin carga en los casos Z&N (2), Z&N (4) y Z&N (5). Los tiempos promedio de subida, retardo y pico se registraron en 1.2 s, 2 s y 2.35 s, respectivamente. Se observó un máximo sobre impulso en los casos Z&N (4) y Z&N (5), con valores de 13.66 y 17.06 RPM, respectivamente. Esto indica que el control en estos casos excede el valor deseado, imponiendo un esfuerzo adicional sobre el motor en comparación con los otros escenarios. En última instancia, se determinó que el rendimiento óptimo se alcanza con Z&N (4), que evita el sobre impulso y presenta un error menor en comparación con los otros casos.
4.3 Prueba eléctrica con carga
Los resultados indican que, para cualquier valor de velocidad establecido, el regulador compensa la disminución de velocidad debido al aumento de peso mediante un incremento en el voltaje a la salida del regulador de corriente alterna (ver Fig.6a). La corriente nominal del motor (ver tabla IV) es mayor que el consumo de corriente registrado en la Fig. 6b. Esto se debe a que la programación y el control PID limitan la oscilación a un máximo de 300 RPM, lo cual es inferior a la velocidad previa a la remanufactura y, por tanto, requiere un menor consumo de corriente. Finalmente, la diferencia en el consumo de corriente entre el peso de 5 kg y el vacío (0 kg) es de solo 0,1 A, lo que indica que la potencia consumida depende principalmente de la tensión regulada.
Medir las características eléctricas de la máquina es importante para conocer la potencia y determinar si la regulación de corriente alterna es efectiva, por lo tanto, estos resultados demostraron el correcto funcionamiento del regulador, así como el consumo de corriente dentro del rango de consumo esperado del motor.
4.4 Prueba de error de rpm con carga
El proceso de prueba fue evaluado utilizando los datos generados por el código, el cual imprime en serie los valores de tiempo, lecturas de RPM en tiempo real y los puntos de ajuste. Los datos recopilados de cada prueba de velocidad se almacenaron en una hoja de Excel, donde se calculó el valor del error cuadrático medio (RMSE) y se representaron gráficamente en las Fig. 7 y 8.
Se muestran que los valores de error son más bajos a 250 RPM para pesos más livianos. Sin embargo, a medida que se incrementa la velocidad y el peso de agitación, el error de RPM tiende a aumentar progresivamente. Se definió un rango específico de velocidades (150 RPM a 250 RPM) y pesos (0 kg a 1 kg), como se observa en las Fig. 7 y 8. En estas condiciones, se registró un error mínimo de 2,08 RPM a 250 RPM y 0 kg, mientras que el error máximo fue de 17,64 RPM a 150 RPM y 1 kg.
4.5 Adquisición de datos de consumo actual del equipo agitador recíproco
Se registró el consumo eléctrico del equipo. Sin embargo, previamente se midió el consumo de la parte electrónica, que es de 0,01 A, el cual debe sumarse al valor total registrado.
A partir de los datos obtenidos en las pruebas del equipo bajo carga, se determinaron la corriente de arranque y la corriente estable dentro del rango de velocidad establecido (150 RPM a 250 RPM) y de peso (0 kg a 1 kg).
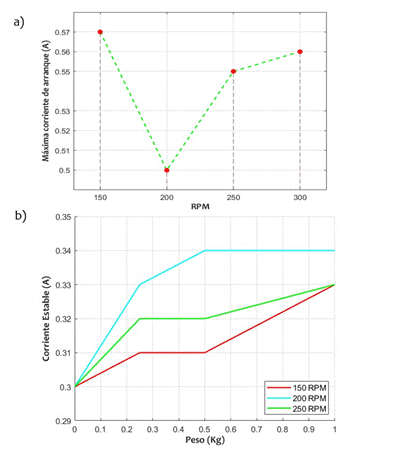
Para establecer la corriente de arranque, se compararon los valores máximos correspondientes a diferentes pesos a una velocidad específica. El valor más alto obtenido, como se muestra en la Fig. 9, fue de 0,57 A, por lo que se estableció una corriente de arranque de 0,58 A.
La corriente estable del equipo se calculó promediando los valores más altos de corriente estable para cada velocidad. En la Figura 8, se observan valores máximos de corriente estable de 0,33 y 0,34 A; es importante considerar que a estos valores se debe agregar 0,01 A. Por tanto, al promediar los valores de corriente, se obtiene un valor aproximado de 0,34 A como corriente estable del equipo.
TABLA III Valores determinados bajo el segundo método de Ziegler-Nichols y ajuste manual
| Constantes de control PID | |||
| Kp | Ki | Kd | |
| Z&N (1) | 3 | 6.0 | 0.375 |
| Z&N (2) | 3.3 | 6.2857 | 0.4331 |
| Z&N (3) | 3.6 | 6.2609 | 0.5175 |
| Z&N (4) | 3.9 | 9.1764 | 0.4144 |
| Z&N (5) | 4.2 | 9.3334 | 0.4725 |
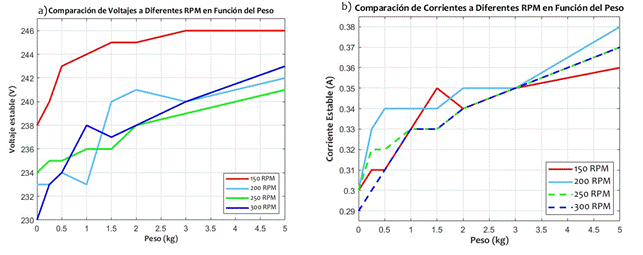
Fig. 6 Corriente y voltaje estables de la máquina a velocidades establecidas sometida a diferentes pesos a) Voltaje vs peso b) Corriente vs peso.
CONCLUSIONES
La implementación del método de control PID con el método de sintonización de Ziegler-Nichols resultó exitosa para mantener la velocidad deseada del agitador dentro del rango de 150 a 250 RPM con un rango de peso de 0 kg a 1.5kg. La corrección de errores mediante el sistema de lazo cerrado permitió estabilizar rápidamente la velocidad del motor con un error porcentual mínimo. Las pruebas de control permitieron determinar y ajustar las constantes de control (Kp, Ki, Kd), logrando tiempos de estabilización y errores porcentuales óptimos. Los valores ajustados según el método de Ziegler-Nichols mostraron una respuesta del sistema eficiente, con un tiempo de asentamiento promedio de 3 segundos mostrada en la Figura 5. Las mediciones eléctricas realizadas a diferentes velocidades y cargas demostraron la efectividad del regulador y el consumo de corriente bajo, ya que la corriente de arranque del equipo se estableció en 0.58 A, mientras que el corriente estable promedio fue de 0.34 A. La evaluación del error de RPM bajo diferentes condiciones de peso y velocidad indicó que, en el rango de 150 RPM a 250 RPM con un peso de 0 kg a 1 kg, el error de agitación fue mínimo. Este análisis identificó un desempeño óptimo del agitador, con un máximo error de 17.64 RPM en las condiciones más desafiantes. Este proyecto demuestra cómo la readaptación de equipos antiguos utilizando componentes de bajo costo y tecnología accesible, como Arduino, puede ser efectiva tanto desde el punto de vista económico como ambiental. La reutilización del motor de CA y el chasis metálico, junto con el desarrollo de un control eficiente, resalta la viabilidad de integrar prácticas de economía circular en el diseño y operación de equipos de laboratorio.
El diseño propuesto es adaptable a una variedad de equipos de laboratorio, como agitadores de placas, mezcladores de soluciones químicas, la homogenización de cultivos microbiológicos, dispersión de partículas en análisis de suelos y simuladores sísmicos en miniatura, ampliando su aplicabilidad en experimentos científicos [4] [5] y [6]. Esta investigación ofrece una solución económica y ambientalmente sostenible para la fabricación y optimización de equipos de laboratorio, fomentando la innovación en la enseñanza de ciencias experimentales y destacando el potencial del hardware de bajo costo para contribuir a un modelo de economía circular.