Introducción
El agua es un recurso fundamental para el crecimiento y desarrollo de las regiones en todo el mundo, sin embargo, el agua es un recurso limitado ya que menos de 1 % del agua de la tierra es fácilmente disponible (Olofintoye, Adeyemo y Otieno, 2013). Pero las necesidades por el agua aumentan debido al crecimiento de la población que se espera alcanzar los 8,79 mil millones en 2100 (Vollset et al., 2020), el desarrollo de los sistemas agrícolas que demanda entre el 70 y 80 % del agua (Elbeltagi et al., 2020) y las tendencias del cambio climático que podrían incrementar la evapotranspiración en 7 % y 12 % durante las décadas de 2050 y 2080 (Mandhi, Sanaz y Samad, 2017). En consecuencia, la gestión del agua es clave para el desarrollo sostenible en los próximos años.
La estimación de la evapotranspiración es un proceso complejo, ya que esta depende de diversos factores tales como las variables meteorológicas, características anatómicas y fisiológicas de la vegetación y las prácticas de manejo (Olivares et al., 2018). Por lo tanto, para determinar la demanda de agua por el suelo y la planta se ha estandarizado el concepto de Evapotranspiración de Referencia (ETo), donde se asume que la ETo es afectado solamente por las variables meteorológicas (Silva y Mendoza, 2020; Villa et al., 2021).
La estimación precisa de la ETo es un proceso no lineal y complicado que depende de varios parámetros climáticos y su interacción entre ellos (Alam et al., 2024), pero también es una de las variables hidrometeorológicas más importantes para la gestión del recurso hídrico, la planificación del riego, el equilibrio hídrico y la modelización de los ecosistemas (Chu et al., 2019; Pour et al., 2020; Jerin et al., 2021).
La fórmula de Penman-Monteith (FAO56-PM) sugerida por Allen et al. (1998), es globalmente aceptado como el método robusto y estándar para la estimación de la ETo (Salam et al., 2020; Yang et al., 2020). Sin embargo, este método es restringido en regiones en desarrollo con carencia de datos de radiación solar y la velocidad del viento (Islam y Alam, 2021); las cuales generalmente no se encuentran en las estaciones meteorológicas convencional del Perú, especialmente en la cuenca del río Mosna; donde solamente existe una estación meteorológica del SENAMHI.
Por lo tanto, en el desarrollo de los modelos para el cálculo de la ETo, es preciso determinar a priori las correlaciones entre las variables que se utilizan para la determinación de la ETo, por lo que en el presente estudio se adoptó el Análisis de Componentes Principales (PCA) y la Clasificación Jerárquica Ascendente (CJA), por tratarse de herramientas ampliamente utilizados en los análisis multivariados. Por todo lo expuesto anteriormente, el objetivo de la presente investigación fue determinar mediante el análisis de componentes principales y la clasificación jerárquica las variables más significativas que influyen en la estimación de la ETo con el método de FAO Penman-Monteith.
Materiales y Métodos
Área de estudio
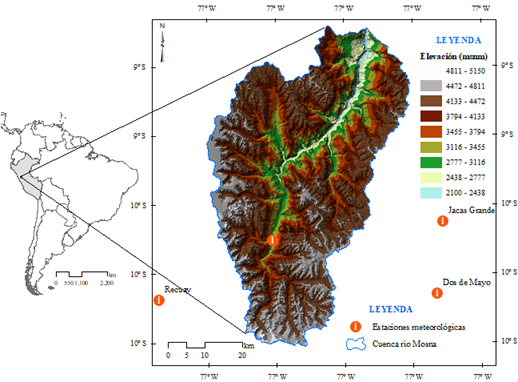
La cuenca del río Mosna ubicada en la sierra central del Perú forma parte de una de las vertientes del marañón. Políticamente la cuenca se sitúa en las provincias de Huari y Antonio Raymondi del departamento de Ancash, cuyas coordenadas geográficas están entre 09° 04' 10'' y 10° 13' 40'' sur 69º 56' 00'' y 77º 10' 10'' oeste. Altitudinalmente se extiende desde la desembocadura del río Marañón a 1970 m.s.n.m. hasta los 5504 m.s.n.m (ANA, 2015).
Variables meteorológicas
La serie histórica de las variables meteorológicas de temperatura mínima, temperatura máxima y la humedad relativa de las estaciones meteorológicas de Chavín, Chiquián, Dos de Mayo, Jacas Grande, Piscobamba, Pomabamba, Recuay y Yungay fueron proporcionados por el SENAMHI. La radiación solar se calculó con la ecuación descrita por Allen et al. (1998), mientras que la velocidad del viento se descargó del sistema NASA-POWER, en vista de que este sistema es uno de los más utilizado para el cálculo de la ETo (Ndiaye et al., 2020; Srivastava et al., 2020), especialmente por su actualización permanente y de fácil acceso.
Cálculo de la evapotranspiración de referencia
La evapotranspiración de referencia se estimó con la ecuación estándar de la FAO Penman-Monteith, propuesto por Allen et al. (1998).
Donde:
ETo es la evapotranspiración de cultivo de referencia (mm/día)
Rn es la radiación neta en la superficie del cultivo (MJ/m2/día)
G es la densidad de flujo de calor en el suelo (MJ/m2/día)
T es la temperatura media diaria a 2 m (ºC)
U2 es la velocidad promedio del viento (media de 24 h) a 2 m (m/s)
es es la presión de vapor de saturación (kPa)
ea es la presión real de vapor (kPa)
es-ea es el déficit de presión de vapor a 2 m (kPa)
∆ es la pendiente de la curva T vs presión de vapor de saturación (kPa/ºC)
γ es la constante psicrométrica (kPa/ºC)
Se utilizó el software CROPWAT versión 8,0 para el cálculo de la evapotranspiración de referencia mensual en la cuenca del río Mosna.
Análisis de componentes principales (PCA)
El análisis de componentes principales se realizó de la matriz de datos, ordenados en líneas las 8 estaciones meteorológicas y en columnas las 5 variables meteorológicas como la temperatura mínima, temperatura máxima, humedad relativa, velocidad del viento y la radiación solar, así como también la evapotranspiración de referencia.
Dado que las variables presentan diferentes varianzas y unidades de medida, se estandarizó el conjunto de datos con la finalidad de homogenizar y dar la misma importancia o carga a las variables (Husson, Lê, y Pagès, 2016), la estandarización se realizó restando a cada valor la media y dividiendo por la desviación estándar de cada variable.
La representación geométrica de las variables en el plano multidimensional se estudió empleando la distancia Euclidiana (d2), la calidad de representación de las variables (Cos) y la contribución (Ctr) de estas en la formación de los componentes principales se analizaron con las siguientes relaciones definidas por Husson, Lê y Pagès (2016):
Donde: l y k son puntos en el espacio de I dimensiones (número de estaciones)
Clasificación jerárquica ascendente (CJA)
Con los resultados del PCA, se realizó el agrupamiento de las variables meteorológicas y la ETo de cada uno de las estaciones, para determinar la similaridad entre las variables en estudio se utilizó la distancia Euclidiana, y la calidad de la representación del dendrograma fue analizada con el teorema de Huygens (Husson, Lê y Pagès, 2016) que se expresa como:
Donde: X es la media de x, Xq es la media de x en la clase q
Para el análisis estadístico multivariado de componentes principales y la clasificación se utilizó el software RStudio integrado en el lenguaje R versión 4,3,0.
Resultados y Discusiones
Análisis de componentes principales (PCA)
Estandarización de las variables meteorológicas y la ETo
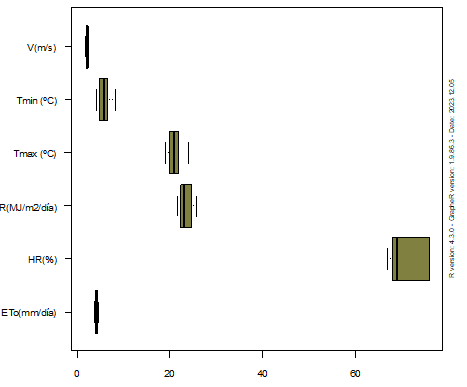
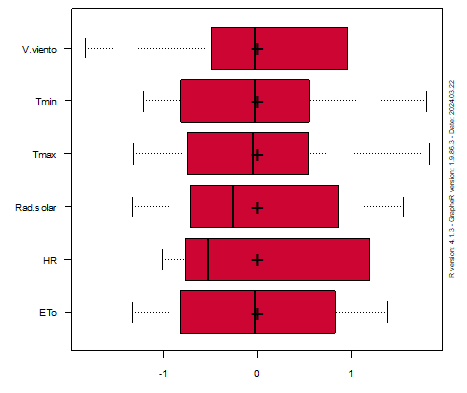
En el presente estudio, el análisis de componentes principales se realizó sobre la matriz de datos cuantitativos como la temperatura mínima (ºC), temperatura máxima (ºC), humedad relativa (%), velocidad del viento (m/s), radiación solar (MJ/m2/día) y la ETo (mm/día) que presentan varianzas de 1,96, 2,43, 16,70, 0,05, 2,14 y 0,09 respectivamente. Dado que las variables en estudio presentan diferentes varianzas y unidades de medida se realizó la estandarización del conjunto de datos, con la finalidad de homogenizar las unidades de medida tal como indican Husson, Lê y Pagès (2016), además, mediante el proceso de estandarización se transformó las variables originales en nuevas variables de media cero y de desviación estándar unitaria. Las variables originales y estandarizadas se presentan en las Figuras 2 y 3.
Elección del número de componentes principales
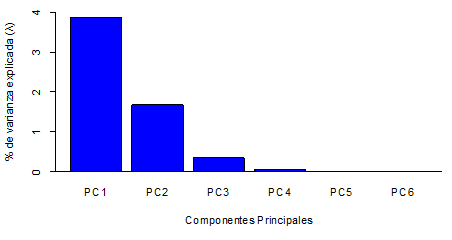
Existen diversos métodos para la selección del número de componentes, en este estudio se utilizó la proporción de varianza explicada, donde solamente los dos primeros componentes (PC) permiten explicar el 92,80 % de varianza de la matriz de datos de 8x6, con valores propios o eigenvalores de λ1 = 3,881 % y λ2 = 1,687 % respectivamente como se observa en la Figura 4. Los demás componentes que presentan porcentajes de varianza inferiores al 1 % aporta información redundante o superfluo como explican Aldás y Uriel (2017). Por lo tanto, se utilizó únicamente los dos primeros componentes para la interpretación de las variables meteorológicas en el plano multidimensional.
Análisis de las variables meteorológicas y la ETo
Las relaciones entre las variables y las componentes se les conoce como cargas, el valor de los vectores varia de -1 a + 1, las variables que forman ángulos agudos indica relación directa, ángulos llanos relación inversa y los ángulos rectos muestra la falta de correlación. También, las variables más alejadas del centro del círculo de correlación aportan mayor variabilidad o calidad de representación (Cos2).
Como el PC1 representa la más alta varianza total de 64,69 %, las variables vinculadas a este componente son los más importantes en la estimación de la ETo con el método de FAO Penman-Monteith. Las variables de temperatura máxima, radiación solar, ETo, humedad relativa y velocidad del viento tienen las más altas cargas en el PC1 según el criterio de Lei (2014) (>0,75) con valores de 0,815, 0,932, 0,958, -0,803 y -0,782 respectivamente (Figura 5 y Tabla 1). Es decir que la ETo incrementa con el aumento de la temperatura máxima y la radiación solar y esta disminuye con el aumento de la humedad relativa y en una menor medida con la velocidad del viento.
Resultados similares a estas afirmaciones fueron encontrados por Núñez-González et al. (2019), quienes al analizar el comportamiento de la ETo estimada con el método estándar en la cuenca Lerma-Chapala de México, encontraron que el incremento de la radiación y una disminución de los valores de la humedad relativa generan aumentos significativos en los niveles de la evapotranspiración de referencia.
Otro estudio reportado por Ikudayisi y Adeyemo, (2016) sobre la influencia de las variables meteorológicas en la ETo en el sistema de irrigación de Vaalharts en Sud África, encontraron que la temperaturas mínima, máxima y la velocidad del viento son los más importantes en la estimación de la ETo y la humedad relativa tiene menor implicancia en la ETo, resultados similares fueron encontrados en esta investigación, a excepción de que la velocidad del viento tiene una relación inversa con la evapotranspiración de referencia. Por lo tanto, surge la necesidad de evaluar el efecto de esta variable sobre la ETo utilizando datos medidos en situ, que a la fecha las estaciones meteorológicas tomadas en este estudio no presentan registros de la velocidad del viento.
Del mismo modo, el efecto significativo de la temperatura máxima y la radiación global en la determinación de la ETo mediante modelos empíricos es mencionada por Santos et al. (2021) en la investigación sobre la evapotranspiración en las diferentes regiones agrícolas en el sur de Brasil, también, los autores indican la poca contribución de la humedad relativa y la velocidad del viento en la determinación de la ETo, no obstante, estas dos últimas variables meteorológicas si influyen de forma negativa en la variación de la ETo calculada en el área de estudio de esta investigación como se observa en la Figura 5 y Tabla 1.
Como se observa en la Figura 4 y Tabla 1, el PC2 muestra alrededor de 28,11 % de la varianza total, según la clasificación propuesta por Lei (2014) (>0,75), este componente tiene una fuerte correlación de 0,895 con la temperatura mínima, es decir que esta variable tiene menor importancia con respecto a otras variables como la temperatura máxima en la estimación de la ETo con el método de FAO Penman-Monteith. Resultados semejantes fueron encontrados en la investigación sobre la predicción de la ETo con algoritmos híbridos y el análisis de compontes principales en suroeste de China realizado por Zhao et al. (2021), quienes señalan que los factores que más influyen en la ETo estimado con el método estándar son la temperatura máxima, la presión atmosférica y las horas de sol. Los efectos de estas dos últimas variables en la evapotranspiración no se avaluaron como tal en este estudio, queda como perspectiva para las próximas investigaciones en la cuenca del río Mosna.
Tabla 1 Análisis de las variables meteorológicas y ETo en los dos primeros componentes principales
| Variables | Cargas | Cos2 | Contribuciones | |||
|---|---|---|---|---|---|---|
| PC1 | PC2 | PC1 | PC2 | PC1 | PC2 | |
| Tmin (ºC) | -0,417 | 0,895 | 0,174 | 0,802 | 4,490 | 47,518 |
| Tmax (ºC) | 0,815 | 0,516 | 0,664 | 0,266 | 17,098 | 15,775 |
| HR (%) | -0,803 | -0,466 | 0,646 | 0,217 | 16,613 | 12,852 |
| V(m/s) | -0,782 | 0,498 | 0,611 | 0,248 | 15,736 | 14,682 |
| R(MJ/m2/día) | 0,932 | -0,298 | 0,869 | 0,089 | 22,396 | 5,262 |
| ETo (mm/día) | 0,958 | 0,257 | 0,918 | 0,066 | 23,647 | 3,912 |
| Eigenvalores | 3,881 | 1,687 | 3,881 | 1,687 | 3,881 | 1,687 |
| % varianza | 64,69 | 28,11 | 64,69 | 28,11 | 64,69 | 28,11 |
| % varianza acumulada | 64,69 | 92,80 | 64,69 | 92,80 | 64,69 | 92,80 |
Utilizando los vectores propios o eigenvalores que se presenta en la Tabla 1, las puntuaciones en las componentes principales PC1 y PC2 se pueden determinar con las siguientes ecuaciones.
PC1 = -0,417xTmin + 0,815xTmax - 0,803xHR - 0,782xV + 0,932xR + 0,958xETo
PC2 = 0,895xTmin + 0,516xTmax - 0,466xHR + 0,498xV - 0,298xR + 0,257xETo
Otro estudio desarrollado recientemente por (Raza et al., 2023) sobre la modelización de la ETo mediante el análisis de componentes principales (PCA) en diversos entornos climáticos de Pakistan, demuestra que las temperaturas máximas, mínima y las horas de sol son las variables efectivas para el cálculo de la ETo, sin embargo, en este estudio la temperatura mínima resulta ser una variable menos efectiva en la estimación de la ETo en el entorno de la cuenca del río Mosna.
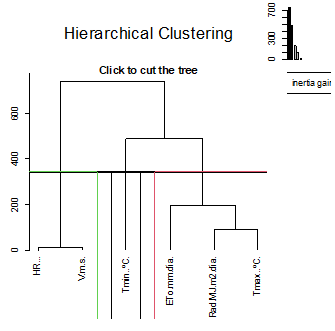
Con los resultados del PCA, se realizó la clasificación jerárquica con la finalidad de determinar la similaridad entre las variables meteorológicas, en la Figura 6 se observan tres clases homogéneas, la clase 1 (rojo) agrupa la temperatura máxima y la radiación solar que son las variables más influentes en el cálculo de la ETo, clase 2 (verde) conformada por la humedad relativa y la velocidad del viento son también variables que afectan de forma inversa el comportamiento de la ETo; mientras que la clase 3 (negro) que contiene la temperatura mínima relacionado al PC2 es la menos importante en la estimación de la ETo con FAO Penman-Monteith.
Conclusiones
El objetivo de esta investigación fue determinar mediante el análisis estadístico multivariado basado en correlaciones las variables más importantes en la estimación de la ETo utilizando el método de FAO Penman-Monteith en la cuenca del río Mosna. Se analizaron una matriz de 5 variables que son fundamentales para el cálculo de la ETo en las 8 estaciones meteorológicas. Los resultados del análisis de componentes principales y la clasificación jerárquica muestran que la temperatura máxima, la radiación solar, humedad relativa y la velocidad del viento son las variables más importantes en la estimación de la ETo, otra variable como la temperatura mínima tiene menor importancia en la evaluación de la ETo con una varianza de 92,80 % en los dos primeros componentes (PCA1 y PCA2).
Por tanto, se puede concluir que el PCA y CJA son herramientas muy poderosas para reducir la dimensionalidad de las variables meteorológicas de entrada y extraer las más significativas para el cálculo de la ETo, no obstante, el uso de las variables meteorológicas en particular la velocidad del viento requiere la validación en el campo para una mayor confiabilidad.












 uBio
uBio