1. INTRODUCCIÓN
Los modelos matemáticos que se construyen en base a la experiencia están siendo ampliamente desarrollados y aplicados a un ritmo cada vez mayor durante las últimas cuatro décadas, debido a la mejora e innovación de los modelos y metodologías que se producen de forma colectiva, y a la alta demanda que surge de la necesidad de dar atención a la problemática de la contaminación de los recursos hídricos [1][2][3].
Al correr de los años el avance de la industria ha conllevado a mejorar las condiciones de vida de las personas, pero también ha significado un mayor uso del agua y una mayor contaminación de los sistemas acuáticos [4], en consecuencia, el control de la contaminación y la gestión integrada de sus recursos se ha vuelto un tema de prioridad mundial [1]
Los ríos son cuerpos de agua que durante su paso a través de una cuenca sufren afectaciones [6] por las represas de agua, los diques de contención, los encauzamientos [7] [8], y otras obras hidráulicas que alteran el flujo del río, produciéndose una retención del agua y sedimentos. Los embalses pasan a ser cuerpos de agua pobres en oxígeno que al ser vertidos al río disminuyen la capacidad de auto purificación del mismo [6]. Las actividades antropogénicas por medio de los sistemas sépticos, tratamiento de desagües, descargas de aguas pluviales, escorrentía agrícola, descargas industriales [9] y las canteras son fuentes importantes de materia orgánica que se descargan a los ríos [7] [8] y que se suman a la carga de materia orgánica natural proveniente del entorno terrestre, que resulta por la precipitación atmosférica e infiltración en la cubierta vegetal, a través de las capas orgánicas y capas minerales del suelo [9], ingresando al río como fuente de contaminación alóctona [10]. Otra fuente natural de materia orgánica es la autóctona [9] [10], que comprende compuestos de mono y polisacáridos, aminoácidos, proteínas, ácidos nucleicos, ácidos orgánicos, lípidos y ácidos grasos [9], los cuales se forman a partir de la descomposición de la biomasa microbiana y vegetal de las cianobacterias, algas y de los macrófitos que habitan el ecosistema acuático del río [9].
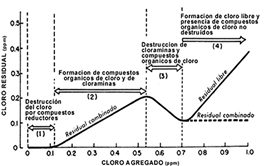
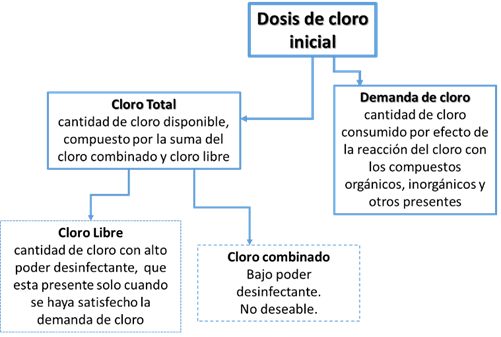
La materia orgánica natural es una mezcla de numerosos compuestos orgánicos que se categorizan según su polaridad (hidrofóbicos, hidrofílicos) y propiedad ácida/neutro/básico. Si bien la materia orgánica natural no puede medirse directamente, existen parámetros sustitutos para su medición, tales como el carbono orgánico total (TOC), carbono orgánico disuelto (COD), absorbancia ultravioleta a 254nm (UV254), absorbancia ultravioleta específica (SUVA) y la demanda química de oxígeno (DQO) [9] [11] [12]. Todas estas descargas de contaminantes impactan y deterioran la calidad del agua de los ríos, que, al ser captada por una Planta de Tratamiento para la producción de agua potable, requerirá de la aplicación de cloro en dosis suficientes para: i) satisfacer la demanda de cloro y ii) proveer de un residual de cloro libre en el agua potable producida, a fin de asegurar que se mantenga su calidad hasta la entrega al consumidor. La demanda de cloro, es la cantidad de cloro consumida por la reacción del cloro con los compuestos orgánicos e inorgánicos presentes en el agua, tal como se presenta en la Fig. 1. La reactividad entre el cloro y los compuestos inorgánicos es rápida no así con los compuestos orgánicos, por lo que una fuente de abastecimiento con mayor contenido de materia orgánica es susceptible de registrar una mayor demanda de cloro [13].
(1) El cloro reacciona con los agentes reductores presentes y no forma un residual de cloro detectable. La dosis de cloro consumida representa la demanda inmediata [6].
(2) El cloro reacciona con el amoniaco y aminas orgánicas para formar cloro residual combinado; terminada la reacción se forma cloro residual libre en cantidad suficiente para oxidar las cloraminas [6].
(3) Oxidación de cloraminas, este proceso continúa hasta que todos los compuestos de cloro-amoniaco desaparecen [15]. La destrucción de las cloraminas reduce el cloro residual, formándose óxido nitroso, nitrógeno y tricloruro de nitrógeno.
(4) Concluida la oxidación de todos los compuestos oxidables por el cloro, todo el cloro agregado desarrolla un cloro residual libre. El punto de quiebre, es aquel donde la oxidación de los productos del amoniaco es completa y a partir de la cual aparece el cloro residual libre como HOCl (ácido hipocloroso), OCl- (ion hipoclorito), según sea el pH; acompañado del cloro residual combinado. En la Fig.2se muestra que la suma del cloro residual libre y cloro residual combinado hacen el cloro total. El ácido hipocloroso tiene mayor poder desinfectantes en relación al ion hipoclorito [15] [16].
Se considera que la demanda de cloro del agua ha sido satisfecha cuando a determinada dosis de cloro aplicado se obtienen valores de cloro residual libre [15].
De esta forma se entiende que la demanda de cloro es un parámetro de interés en el control de los procesos de una Planta de Tratamiento de Agua (PTA), pero también un indicador del grado de deterioro de la calidad del agua del rio por efecto del impacto de las descargas de compuestos orgánicos e inorgánicos [13].
En base a la información recopilada se advierte la existencia de pocos artículos científicos sobre modelos matemáticos de demanda de cloro (MMDCL) en ríos.
El propósito de esta revisión sistemática fue hacer una síntesis de los modelos matemáticos desarrollados para predecir la demanda de cloro en agua de río y aportar al conocimiento sobre que tan bien el modelo puede explicar la demanda de cloro a partir de variables físicas, químicas y biológicas influyentes de un área de estudio en particular.
2. ANTECEDENTES
Una de las primeras investigaciones del modelamiento de la demanda de cloro en aguas fue la realizada por Taras [17] en el año 1950, quien desarrolló un modelo empírico de la cinética de la demanda de cloro a partir de la cloración de soluciones puras de varios compuestos orgánicos. Los MMDCL relacionan parámetros de calidad del agua que varían en el tiempo y el espacio, como el pH, absorción ultravioleta, temperatura, turbidez y carbono orgánico disuelto, etc. [18].
Al entrar en contacto el cloro con el agua se produce una reacción con todos los compuestos presentes, esto significa que reacciona con miles de moléculas [18], y la velocidad o lentitud de las reacciones dependerán de la naturaleza química de cada uno de ellos [19]; por lo que se entiende que un MMDCL será específico, particular y restrictivo, según el comportamiento de los contaminantes en el agua de rio.
A la fecha, se han desarrollado más de 100 modelos de calidad de aguas [20][21], que permiten interpretar la carga contaminante presente, la transferencia de contaminantes y el futuro resultado de la relación de coocurrencia entre la fuente de contaminación y la calidad del agua [21]. Los modelos matemáticos para la predicción de la demanda de cloro en agua de río, se han desarrollado a partir de parámetros de calidad como temperatura, pH, COD, entre otros [18].
El desarrollo de modelos que interpretan los procesos que ocurren en un sistema natural, se realiza por la articulación de cuatro componentes esenciales (realidad, modelo conceptual, código y modelo), que están conectados por medio de procesos, los que a su vez comprenden procedimientos que estiman la confiabilidad de dichos procesos [22][23].
Desarrollar un MMDCL se justifica por ser una herramienta de soporte para conocer a priori los cambios de la calidad química y biológica que ocurre a lo largo de la cuenca de los ríos [24][25] [26][27][28]y apoyar en la toma de decisiones para la mejora de la calidad ambiental del recurso hídrico y formulación de estrategias futuras para la gestión de la calidad del agua de los ríos [28].
3. METODOLOGÍA
Se aplicó una revisión sistemática de publicaciones científicas para evaluar el estado actual del conocimiento de los MMDCL siguiendo las instrucciones PRISMA [29]. En concreto, se llevó a cabo una revisión crítica de estudios de casos publicados sobre MMDCL aplicados en aguas de río.
Criterios de Inclusión y Exclusión
La inclusión y exclusión de publicaciones se realizó en base a tres criterios:
i)El estudio se realizó en aguas de río.
ii) Los resultados del estudio deben ser originales y producto de los ensayos experimentales.
iii) El modelo debe implicar la predicción de la demanda de cloro.
Fuentes de Información
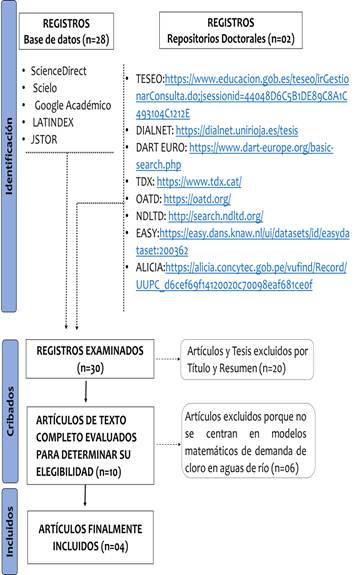
Para la recopilación de los artículos se utilizó la Base de datos electrónica de ScienceDirect, SciELO y Google Académico, sistemas de información de revistas científicas LATINDEX y JSTOR; así como Repositorios Doctorales.
La selección de los estudios se realizó según la Fig.3.Se aplicaron dos niveles de selección para los estudios: por título y resumen, y por texto completo.
Riesgo de Sesgo
Para la identificación del sesgo de publicación, el efecto de cada estudio representado por la métrica R2 fueron integrados aplicando técnicas de análisis estadístico [30][31], como las gráficas en forma de embudo o funnel plot [32]. Si bien este método gráfico es fácil de usar, no es muy fiable para casos en que el número de estudios es pequeño, por lo que es conveniente añadir métodos más objetivos como la prueba de correlación de rangos de Begg y la prueba de regresión lineal de Egger [33][34].
Es de esperar que existan diferencias entre los resultados obtenidos en los estudios primarios, y es precisamente la heterogeneidad estadística la que ofrece una mejor comprensión de la variación de los resultados entre sí [32][34]., la cual se expresa a través del diagrama de árbol o forest plot y utilizando los estadísticos: Prueba de Cochran Q, estadístico I2 de Higgings y coeficiente ( de Kendall.
4. ANÁLISIS DE RESULTADOS
4.1 Selección de estudios
El periodo de la búsqueda bibliográfica fue desde el año 1940 hasta el año 2023. Las palabras clave de búsqueda fueron: “demanda de cloro”, “demanda de cloro en aguas superficiales”, “demanda de cloro en aguas”, “modelo de demanda de cloro en aguas superficiales”, “reacciones de decaimiento de cloro en aguas superficiales” y “cloración de aguas”, las cuales también se colocaron en inglés.
En total se encontraron 28 artículos y 02 Tesis Doctorales, las cuales fueron tratadas siguiendo la guía de revisiones sistematizada PRISMA 2020 para identificar, seleccionar, evaluar y sintetizar las fuentes primarias recopiladas. Se definieron los criterios de inclusión como de exclusión de las fuentes primarias, fijando para ello los criterios de calidad [35] con los cuales se inició la etapa de cribado que consistió en dos niveles de selección:
i)Por título y resumen, se hizo la pregunta:
¿Tiene importancia la referencia para el objeto de la revisión?
ii)Por texto completo, se hicieron tres preguntas:
¿Este artículo o tesis trata sobre la demanda de cloro?
¿Este artículo o tesis trata sobre aguas superficiales, específicamente ríos?
¿Este artículo o tesis formula un MMDCL con métrica estadística de la calidad del modelo?
En el primer nivel se excluyeron 20 artículos, y pasaron 10 artículos a un segundo nivel de selección, quedando finalmente solo 04 artículos. La Fig. 3 muestra el diagrama de flujo [29] de selección de artículos.
4.2 Síntesis de Resultados
Proceso de Selección
Para la presentación y síntesis de los resultados se utilizó el programa Microsoft Excel (hojas de cálculo, tablas y gráficos), así como de la hoja de cálculo avanzada JAMOVI.
Información relevante de cada uno de los artículos fueron plasmados en la Tabla 1, con datos como nombres de los autores, año y título del artículo, título de la revista y numero de citas. La cita es un criterio de evaluación que da una idea subjetiva del reconocimiento de la importancia y calidad del artículo [36][37]. Por medio del Google Académico se identificó que el estudio más citado fue el de M. Abdullah et al (53.6%), seguido de L. Yee. et al (26.4%) [42], G. Zhu et al. (4%) [50] y M. Abdullahi & B. Abdulkarim (3.2%) [45].
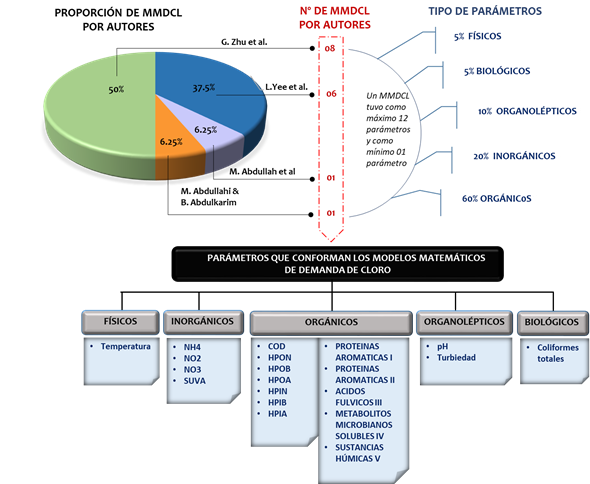
Fig. 4 Proporción de MMDCL por autores y parámetros de calidad de agua que lo conforman. (Elaboración propia)
Parámetros de calidad del agua
De la Tabla IIy la Fig.4, vemos que en la formulación de los MMDCL se utilizaron diferentes tipos de parámetros de calidad de agua: físicos (temperatura), orgánicos (SUVA, COD, fracciones de COD, materia orgánica expresada como 05 fracciones de la región integrada de fluorescencia - RIF), inorgánicos (amonio, nitrito, nitrato), organolépticos (pH, turbiedad) y biológicos (coliformes totales). En la Fig. 4 se observa que en total fueron 20 los parámetros de calidad de agua utilizados en la formulación de los 16 MMDCL; y de éstos, en proporción el 60% fueron parámetros orgánicos, 20% parámetros inorgánicos, 10% parámetros organolépticos, 5% parámetros físicos y 5% fueron parámetros biológicos. En la Tabla II se aprecia que el parámetro pH formó parte en siete de los MMDCL, los parámetros temperatura y amoniaco en dos de los MMDCL, seguido por los parámetros de nitrito, nitrato, carbono orgánico disuelto y fracciones fluorescentes de materia orgánica que participaron en cinco MMDCL, los demás parámetros en un MMDCL. En cantidad de parámetros, como máximo fueron 12 los que formaron parte de un MMDCL y como mínimo un parámetro.
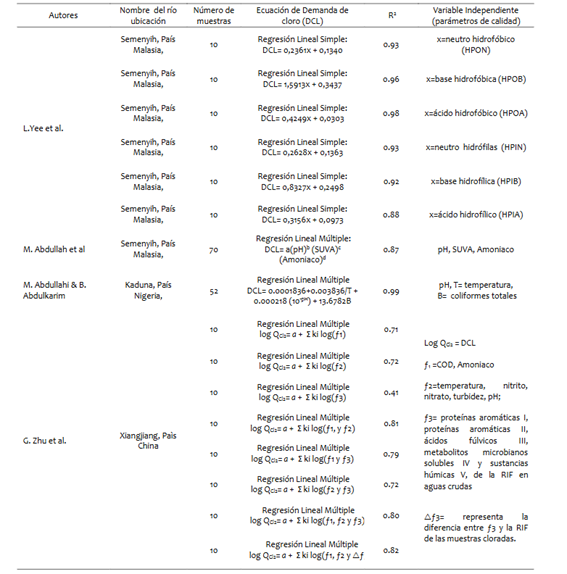
TABLA II Características relevantes de los modelos matemáticos de demanda de cloro de los 04artículos seleccionados
Algunas de las métricas utilizadas para la comparación y selección de modelos de regresión que mejor se ajuste a los datos, son el coeficiente de determinación (R2) y el coeficiente de determinación ajustado (R2 ajustado) [38][39].
En la Tabla II, con respecto a los MMDCL por regresión, se aprecia que los coeficientes de determinación R2 de los dieciséis MMDCL oscilan entre 0.41 y 0.99, por lo que a simple vista pensaríamos que todos los modelos son buenos y por lo tanto los parámetros de calidad son fuertes predictores de la demanda de cloro, sin embargo, podría ser que R2 este sobrevalorado por efecto de la fuerte correlación entre estas variables independientes; los artículos no lo mencionan, pero se asume que esta sospecha fue descartada, así como se asume también que antes de proceder al análisis de regresión, se demostró que se cumplen las suposiciones de normalidad, homocedasticidad, independencia de error y linealidad de los datos [40][41].
La Tabla II muestra que los MMDCL son ecuaciones de demanda de cloro, donde el signo igual indica la existencia de una relación entre el valor de la variable dependiente o demanda de cloro que se pretende predecir y el otro lado con las variables independientes conformados por valores conocidos (números, coeficientes o constantes) y valores incógnitas por reemplazar (parámetros físicos, inorgánicos, orgánicos, organolépticos y biológicos).
Análisis descriptivo de los artículos cribados
Los modelos matemáticos de regresión lineal simple propuestos [42] tienen como variable independiente las fracciones del COD, por considerarlo uno de los temas más importantes en el proceso de tratamiento ya que influye significativamente en las operaciones y la gestión de las Plantas de tratamiento de agua [7][43] y por ser precursor principal en la formación de los trihalometanos durante el proceso de cloración [43]. El COD generalmente se evalúa en el río en puntos cercanos a las descargas de las obras de tratamiento de aguas residuales y su valoración representa la magnitud de su repercusión en el río [44]. El COD está compuesto por sustancias húmicas, de polaridad hidrofóbicas de alto peso molecular, que constituyen del 30-80% de la materia orgánica natural en las aguas [15][43]. De los seis modelos propuestos [42], se identifica que el modelo con variable independiente HPOA tiene el mayor R2 (0.98) y el modelo con variable independiente HPIA tiene el menor R2 (0.88); en suma, por el valor de R2 se entiende que todos los modelos propuestos por los autores explican bien la variabilidad de la variable dependiente, esto es la demanda de cloro.
En cuanto al modelo de regresión lineal múltiple propuesto por M. Abdullahi & B. Abdulkarim [45], incluye tres variables independientes: pH, temperatura y bacterias coliformes, los que consideran que pueden explicar la variación de la calidad del agua cruda y su efecto en el consumo de los diferentes productos químicos utilizadas en el proceso de tratamiento, entre ellos el cloro. En el medio ambiente las bacterias son altamente vulnerables al pH y temperatura, esto por efecto de los diferentes compuestos orgánicos, inorgánicos u otros productos químicos presentes, tales como el cloro [46][16][47]. En el proceso de cloración, la estabilidad del cloro se ve influenciada por el pH. A pH >7.5 predomina la especie OCL-la cual es débil y más estable, a pH <7 predomina la especie HOCL, la cual es más fuerte y más reactiva [46]. La mayor efectividad bactericida la ejerce la fracción de HOCL en relación al OCL-. El incremento de la acción bactericida del cloro se ve favorecida a medida que los valores de pH disminuyen y los valores de temperatura aumentan [46][16][47]. Dependiendo de su concentración, los microrganismos en general ejercen una demanda de cloro, incluyendo aquellos organismos resistentes al cloro. El daño celular por acción del cloro ocurre a nivel de las membranas, interrumpe las funciones metabólicas por destrucción enzimática, degrada las proteínas y daña el ADN. Las sustancias inorgánicas presentes en el agua, tales como sulfuros, tiosulfatos y sales ferrosas tienden a reaccionar fácilmente con el cloro lo que disminuye significativamente sus propiedades bactericidas [47]. Los autores utilizaron una data importante para la construcción del modelo obteniendo un R2 de 0.99.
El modelo de regresión lineal múltiple propuesto por Abdullah et. Al [48], incluye tres variables independientes: pH, SUVA y amoniaco con coeficientes ( de 0.216, 0.237 y 0.576, respectivamente. De los resultados obtenidos del estudio, el análisis estadístico muestra que el amoniaco es la variable independiente con mayor valor del coeficiente (, por lo tanto, el que mayor efecto tiene en el MMDCL; lo que indica que son aguas con cantidad importante de desechos fecales, fertilizantes agrícolas, efluentes de aguas residuales tratadas, etc.; [49]. El amoniaco es un compuesto inorgánico de nitrógeno que al reaccionar con el HOCL produce cloraminas [13] y en ocasiones, es oxidado a nitrógeno gaseoso, nitrato y otras formas de nitrógeno, lo que dependerá de la dosis de cloro, la cantidad de amoniaco, la temperatura y tiempo de contacto[6]. El coeficiente ( de la variable SUVA es mucho menor que el coeficiente ( del amoniaco, por lo que en el agua estaría prevaleciendo una mayor proporción de nitrógeno amoniacal en relación al nitrógeno orgánico. Esta condición prevé que los consumos de cloro siempre serán menores a los ocurridos en caso las proporciones de nitrógeno amoniacal y nitrógeno orgánico fueran a la inversa [15]. Los autores mencionan que existe una relación y similitud entre los coeficientes ( del SUVA y del pH, advirtiendo un nivel de relación mesurado entre ellos y con la demanda de cloro. Los autores utilizaron una data importante para la construcción del modelo obteniendo un R2 de 0.87.
G. Zhu et al., [50], propusieron un modelo de regresión lineal múltiple para determinar el consumo de cloro en aguas. Las variables independientes del MMDCL fueron dispuestos en tres componentes: ƒ1=COD, NH3-N; ƒ2=temperatura, nitrito, nitrato, turbidez, pH; ƒ3= cinco fracciones fluorescentes de la MON. La sensibilidad de los componentes ƒ al modelo fueron medidos a través del coeficiente R2, encontrándose valores de 0.72, 0.71 y 0.41, para ƒ1, ƒ2 y ƒ3, respectivamente; evidenciándose la poca capacidad del componente ƒ3 para predecir el consumo de cloro solo a partir de las fracciones de fluorescencia.
La fluorescencia es un atributo que tiene algunos compuestos orgánicos e inorgánicos de poder captar energía a una longitud de onda específica para luego liberarla en forma de luz a una longitud de onda más larga [51]. El parámetro de COD mide el contenido de materia orgánica de modo general, sin lograr expresar las fracciones hidrofóbicas o hidrofílicas que conforman la materia orgánica, las que pueden ser cuantificadas por medio de la técnica de fluorescencia, la cual se caracteriza por su alta sensibilidad y rápida identificación [52]. Además del COD, la fluorescencia guarda relación con los parámetros sustitutos de la materia orgánica, tales como la demanda química de oxígeno [53] y demanda bioquímica de oxígeno [54]; todos ellos son indicadores para evaluar la calidad del agua [9][51]. En aguas superficiales y subterráneas donde no se producen ingresos de contaminantes antropogénicos, la fluorescencia es determinada, en gran parte, por compuestos húmicos y fúlvicos, y en menor proporción por residuos orgánicos de la flora y fauna presente, tales como el grupo amino aromático de proteínas [51].
Se mejoró la capacidad de predicción del modelo con la combinación de los componentes ƒ1 y ƒ3 con R2 de 0.79 y con la combinación de los componentes ƒ2 y ƒ3 con R2 0.72, esto debido a que la fluorescencia es un buen factor predictor de la DDCL cuando se combina con factores de compuestos inorgánicos como el NH4 y orgánicos como el COD [51] [15] [55].
El cloro, bajo su forma HOCL reacciona rápidamente con el NH3-N para formar cloraminas, y en su paso se forman compuestos cloro: amoniaco que desaparecen a medida que se produce la descomposición de las cloraminas, para dar paso finalmente a la formación cloro residual libre cuya concentración será menor de la que se pudo formar en ausencia de COD [15]. En aguas con alto contenido de NH3-N, se justifica un mayor consumo de cloro debido a la facilidad con la que éstos compuestos reaccionan con el cloro, específicamente el HOCL [13], y mayor será el consumo si además está presente el COD. Los diferentes tipos de ingresos de contaminantes a los cuerpos de agua generan múltiples reacciones que particularizan su nivel de contaminación y en consecuencia su resistencia a la cloración con variación en el consumo de cloro.
Meta-análisis
Riesgo de Sesgo
Los estudios con resultados estadísticamente significativos tienen más posibilidad de ser aceptados y publicados en revistas de alto impacto que los estudios que informan sobre efectos pequeños, poco relevantes [34][56][32][57], lo que puede influir que este tipo de ensayos tengan una menor probabilidad de ser seleccionados en la revisión sistemática. Para minimizar el riesgo de sesgo de selección, se delimitaron los criterios de inclusión y exclusión de los estudios primarios, y se incluyó la búsqueda en Repositorios Doctorales.
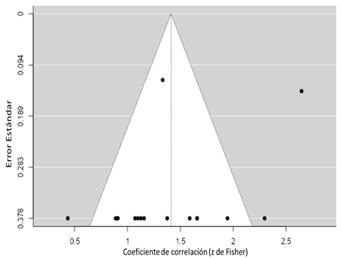
En la Fig. 5. tenemos el efecto (correlación, valores z de Fisher) en el eje X, así como su error estándar en el eje Y. La línea punteada vertical representa el efecto real estimado (z = 1.675), encontrándose a su derecha los estudios que consiguieron un efecto mayor y a su izquierda los que consiguieron un efecto menor. A simple vista se aprecia que la dispersión de los datos con respecto al centro no es equitativa en ambos lados. La gráfica del embudo es un análisis muy subjetivo [58], por lo que su interpretación no es concluyente [33], pues existen factores que pueden afectar la dispersión de los datos en la gráfica, como el tamaño de muestra, la metodología empleada, el tiempo, entre otros factores. Para aliviar estos efectos se utilizó la prueba de correlación de rangos de Begg y Mazumdar y la prueba de regresión Egger [33].
La dispersión de los datos en la gráfica, denota un sesgo de publicación, lo cual puede ocurrir cuando se evalúan estudios cuyo número de muestras es pequeño, por otro lado, influye también las diferencias que puedan existir por el tratamiento de las muestras, y otros como el tamaño de las muestras, la metodología empleada, el tiempo, todos estos factores contribuyen a la heterogeneidad de los datos. Para atenuar estos efectos se utilizó la prueba de correlación de rangos de Begg y Mazumdar y la prueba de regresión Egger [33]. La prueba de correlación de rangos no indica asimetría del gráfico del embudo, pero la prueba de regresión de Egger sí.
TABLA III Evaluación del sesgo de publicación
| Nombre de la Prueba | Valor | p |
| Correlación rangos de Begg y Mazumdar | -0.017 | 0.937 |
| Regresión de Egger | -1.712 | 0.087 |
La prueba de Egger y la prueba de Begg y Mazumdar son pruebas estadísticas para identificar la asimetría en la gráfica del embudo [34], y sugieren la presencia de sesgo cuando el valor de p es menor que 0.1 [33][59]. Entre ellos, el test de Egger es el más sensible [59]. La tabla III, muestra que el valor p para la prueba de Egger fue 0.087 lo que sugiere que hay sesgo de estudios pequeños [34]; y el valor p para la prueba de Begg y Mazumdar fue 0.937, lo que sugiere que existe una correlación entre la unidad estándar del efecto y su variabilidad [34].
Heterogeneidad
Se aumenta el poder estadístico [60], al incrementarse la precisión del resultado total por efecto de la combinación de los resultados individuales de cada estudio; pero antes es necesario que se evalúe la heterogeneidad, la cual refiere al grado de variación observado entre los resultados de los estudios individuales [61]. Las pruebas estadísticas Q de Cochran y el I(2, exponen las diferencias que no son explicadas por el azar y son derivadas de las verdaderas diferencias [60]
Se mide la heterogeneidad de los estudios para determinar si existe similitud entre ellos, utilizando el parámetro Q de Cochran; si el valor obtenido es < 0,05 entonces existe heterogeneidad significativa [33]; sin embargo, cuando el número de estudios es pequeño el parámetro Q pierde potencia por lo que es necesario medir el estadístico I 2 de Higgings cuyo valor oscila entre 0 - 100%, considerándose que existe una heterogeneidad en progreso cuando el valor de I2 es ( 33% [32][33]; otra prueba de heterogeneidad es el Tau cuadrado (((2), que expresa que si no hay diferencias entre las varianzas de los estudios entonces τ²=0, no hay heterogeneidad [58].
En la tabla IVse aprecia que el estadístico I2 es 75.93%, la prueba de Cochran Q es de 89.46 con p<0.001, y el coeficiente ( de Kendall es de 0.265.
Los resultados del análisis de heterogeneidad muestran que el rigor estadístico de los MMDCL es discrepante, esto por las diferencias que existen en el número de muestras del estudio, diferencias por las variables explicativas que conforman los modelos, no solo por el tipo de parámetro sino también por el número de parámetros. Sin embargo, estos resultados acusan un grado de importancia en su análisis puesto que ocurre que la heterogeneidad en los resultados pasa a convertirse en el principal objetivo del meta-análisis, pues es congruente y racional esperar obtener una heterogeneidad importante, pues los MMDDCL se formulan en base a la combinación de las variables o parámetros de calidad característicos de una fuente de abastecimiento de agua - río, donde las reacciones químicas entre sí y con el cloro varían en el tiempo y bajo diferentes escenarios de calidad del recurso hídrico [34].
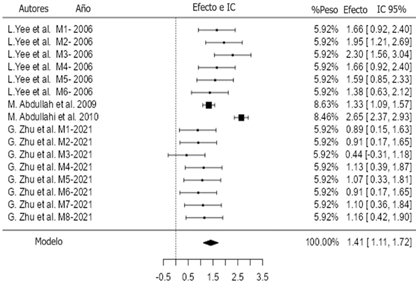
El diagrama de bosque representa la medida estandari zada del efecto de la combi nación de los resultados individuales y la heterogeneidad entre los estudios [34][61].
En la Fig.6. se presenta la medida del efecto (coeficiente de correlación - z) en el eje de las abscisas (eje X) y a lo largo del eje de las ordenadas (eje Y) se sitúan los diferentes MMDCL, ordenados por el año de publicación.
El examen de los residuos estudentizados revelaron que el estudio de Abdullahi tuvo un valor mayor que +/-2.9552 por lo que podría ser un posible valor atípico potencial en el contexto de este modelo. Según las distancias de Cook, el estudio de Abdullahi podría considerarse demasiado influyente.
En el análisis de incluyó un total de k = 16 MMDCL. De la tabla V, se aprecia que el coeficiente de correlación transformado r-a-z promedio estimado de Fisher basado en el modelo de efectos aleatorios fue = 1.41, con intervalos de confianza al 95% de 1.11 a 1.72; por lo tanto, el resultado promedio fue significativamente diferente de cero (z=9.09, p<0.001).
TABLA V Modelo de efectos aleatorios (k=11)
| Posición | Estimado | Error estándar | Z | p | ICI | ICS |
| Intercepto | 1.41 | 0.155 | 9.09 | <0.001 | 1.11 | 1.72 |
Nota: ICI (intervalo de confianza inferior), ICS (intervalo de confianza superior).
En esta revisión sistemática, siguiendo el procedimiento PRISMA, finalmente se seleccionaron 04 estudios primarios, que constituyeron un total de 16 MMDCL propuestos. Existe poca información sobre estudios realizados para modelar la demanda de cloro en aguas superficiales utilizadas como fuente de abastecimiento para uso de consumo humano, específicamente ríos. Todos los MMDCL propuestos por los autores ha sido diseñados a partir de modelos de regresión lineal simple y múltiple.
Evaluar el rendimiento de un modelo matemático, es una forma de conocer la calidad de las predicciones que puede estimar, para ello se hacen uso de diferentes métricas de evaluación [62], siendo una de ellas, y de mayor uso el coeficiente de determinación R2. Esta métrica nos da un alcance de la dimensión de la varianza de la variable dependiente que bien puede interpretar el modelo lineal [63][64][65]. Los autores reportaron el valor de R2 de sus MMDCL propuestos, por lo se utilizó esta métrica para comparar el rendimiento de los 16 MMDCL propuestos [62][63][64]. Aquí se hace una mención importante respecto a los estudios más sistemáticos sobre la demanda de cloro realizados por los autores Douglas Feben y Michael Taras en el año 1950, los que han servido de inspiración y base del conocimiento en estudios posteriores relacionados sobre la cinética de la cloración en aguas y aguas residuales. El MMDCL propuesto por los autores no forma parte de los estudios seleccionados para la presente revisión sistemática, por la no disponibilidad de los coeficientes R o R2 en los artículos científicos publicados [17][66]; situaciones como ésta se considera una pérdida de datos para la presente investigación [67].
En la Tabla II, se precisan las características de los 16 MMDCL propuestos, donde todos son modelos de regresión lineal y con un valor R2 con rigor competitivo [64]. Las variables independientes que conforman los MMDCL corresponden a los contaminantes más representativos de la fuente de agua por su capacidad de reacción con el cloro expresado como consumo o demanda de cloro, cuyo valor es dato de entrada importante para las consignas de operación de los procesos de desinfección en una Planta de Tratamiento de Aguas.
Según la Tabla II, el MMDCL de M. Abdullahi & B. Abdulkarim [45] tiene un R2 de 0.99 lo que significa que dentro de todos los modelos propuestos es el que mejor logra explicar la variabilidad de la o las variables independientes [63][64]; seguido por los seis MMDCL propuestos por L. Yee et al. [42] En realidad, puede considerarse que todos los MMDCL propuestos alcanzaron un [42] valor de R2 importante que estuvo entre 0.86 - 0.99, a excepción de uno de los MMDCL propuesto por G. Zhu et al. [50], con un R2 de 0.46, donde la variable independiente estuvo compuesta por cinco fracciones de fluorescencia de la materia orgánica natural. En forma global, las variables independientes utilizadas en los MMDCL propuestos evidencian una tendencia que corrobora el comportamiento del cloro cuando entra en contacto con una fuente de agua superficial, como el río que, usualmente se caracteriza por contaminación de tipo orgánico e inorgánico [15]. De los 16 parámetros de calidad (variables independientes) que formaron parte de los MMDCL propuestos por los autores, fueron el pH (13.46%), la temperatura (11.54%) y el NH3 (11.54%) las variables independientes más utilizadas, lo cual es coherente con el mecanismo de desinfección del cloro, donde la velocidad de reacción está en función de la temperatura y el pH, y en consecuencia de las proporciones que se formen de cloro residual libre como el HOCL y otra parte como OCL- [15][68]. El cloro libre reacciona rápidamente con el NH3 para formar cloraminas [15] que son compuestos de cloro combinado de bajo poder oxidativo, y con la misma rapidez reacciona con compuestos orgánicos e inorgánicos (Fe++, Mn++, NO-2, H2S) para formar cloro combinado sin ningún poder desinfectante o demanda de cloro.
El parámetro de materia orgánica (fracciones fluorescentes), como el COD, formaron parte de los MMDCL propuestos por los autores en 9.62%, y son compuestos con baja velocidad de reacción con el cloro, de ahí que su presencia en el agua es de alta importancia en la operación de las Plantas de Tratamiento de agua, sobre todo cuando su proporción es mayor que la del nitrógeno amoniacal, pues ocasiona una demanda de cloro lenta y progresiva que obliga a incrementar las dosis de cloro para satisfacer no solo la demanda de cloro presente sino también lograr mantener residuales de cloro libre en el agua potable producida.
El SUVA y las fracciones hidrofóbicas e hidrofílicas de COD, son parámetros sustitutos [9] que expresan el contenido de materia orgánica y su inclusión en los MMDCL propuestos por los autores fue de 1,92%, igual porcentaje de inclusión en los MMDCL propuestos obtuvo el parámetro de coliformes totales, el cual incluye una amplia variedad de bacilos aerobios y anaerobios facultativos, gramnegativos y no esporulados que pueden sobrevivir y proliferar en el agua. Son bastante sensibles a la acción del cloro.
La ecuación del MMDCL de Abdullahi & B. Abdulkarim [45] con R2 de 0.99, incluye constantes que afectan a las tres variables independientes (pH, temperatura y coliformes totales) y se suma una cuarta constante para corregir los posibles efectos de aquellas variables no incluidas en la ecuación del MMDCL. Los autores determinaron la derivada del error del modelo propuesto para encontrar los valores de las constantes que mejoren el rendimiento del MMDCL. La derivada como función matemática expresa la velocidad de cambio de una variable con respecto a otra [69]. El MMDCL propuesto por M. Abdullah et al., tiene un R2 de 0.87, y tiene como variables independientes al pH, SUVA y amoniaco los cuales están fuertemente ligados a los mecanismos de reacción del cloro en el agua [9][15] y en consecuencia este modelo logra explicar la variabilidad de las variables que producen la demanda de cloro. En los MMDCL propuestos por G. Zhu et al. [50], las ocho variables independientes fueron agrupadas en tres componentes ƒ, y se aprecia que a medida que se aumenta el número de factores al MMDCL aumenta el R2.
En modelos multivariados, a medida que se aumentan las variables independientes el R2 aumenta también, independientemente si la nueva variable es importante o no [70]. El coeficiente R2es una métrica que no diferencia entre una regresión lineal simple y una múltiple con n predictores, a diferencia de la métrica R2 ajustado que advierte la cantidad de predictores y de datos disponibles, y castiga la adición de predictores que no ajustan significativamente la capacidad de predicción del modelo.
De la Fig. 6 de la gráfica del embudo se interpreta que existe sesgo de publicación por estudios de tamaño pequeño, lo cual puede ser afectado por factores que no pueden ser controlados en el presente estudio, tales como el número de muestras, el procedimiento metodológico, entre otros; y para evitar su efecto se utilizó la prueba de correlación de rangos de Begg y Mazumdar y la prueba de regresión Egger [33], concluyendo que no existe asimetría en el gráfico en embudo.
La Fig. 6 diagrama de bosque indica que el MMDCL de Abdullahi & B. Abdulkarim [45] tiene poder estadístico de predicción de 8.46, efecto acotado de 2.65 y un error de estimación medio de 0.56; en comparación con el MMDCL de M. Abdullahi et al. [42], que tiene un mayor poder estadístico de predicción de 8.63, un menor efecto acotado de 1.33 y un error de estimación menor de 0.48; y en cuanto al MMDCL de L. Yee et al. [42], tiene poder estadístico de predicción mucho menor de 5.92, efecto acotado medio de 2.30 y un error de estimación mucho mayor de 1.48. Todos los demás MMDCL tiene un bajo peso estadístico, e incluso uno de los MMDCL propuestos por G. Zhu et al. [50], con variable independiente ƒ3 (fracción fluorescencia materia orgánica) cruza la línea vertical de no efecto, por lo que se concluye su poco rendimiento como predictor, lo que se corrobora con el valor de o,41 del R2 del modelo. Solo en el MMDCL propuesto por los autores Abdullahi et al. [45], se incluyó el parámetro biológico de coliformes totales. Tal vez, la baja inclusión del parámetro de coliformes totales como variable predictora, se deba al tiempo que se demora en obtener los resultados de los análisis por el método del Número Más Probable; sin embargo, hoy por hoy existen métodos enzimáticos y de fluorescencia para la rápida detección de bacterias coliformes, así como de técnicas rápidas de Biología Molecular.
Los MMDCL de la Tabla II se expresan como ecuaciones que pueden aplicarse a diferentes casos de estudio de aguas captadas de un río como fuente abastecimiento, tan solo utilizando las mismas ecuaciones y cambiando los valores de las variables independientes (parámetros de calidad y constantes). Para la selección del MMDCL además se debe considerar varios factores como: i) conocimiento previo del o los contaminantes que ejercen la demanda de cloro en el agua de río, ii) contar con una data para probar la aplicabilidad del modelo, iii) recursos disponibles por costo de aplicación del modelo y iv) obtener un índice de desempeño aceptable del modelo aplicado (R2, R2 ajustado, error cuadrático, etc), con lo cual se evidencia que el valor de la demanda de cloro obtenida con la aplicación del modelo matemático representa de forma aceptable el valor de la demanda de cloro obtenida en ensayos de laboratorio; caso contrario, es necesario ajustar los valores de los constantes o verificar la estructura del modelo, con el fin de reconocer las fuentes de error.
Los MMDCL de L. Yee et al [42], definen la capacidad y aplicación de sus modelos para aguas de río caracterizados por contenidos de COD. El modelo de M. Abdullahi et al. [45], considera su aplicación en aguas de rio donde el pH, SUVA y el amoniaco son los que ejercen la demanda de cloro. Además, el modelo de M. Abdullahi & B. Abdulkarim [45]se circunscribe a la demanda de cloro ejercida por la presencia de coliformes totales, y los parámetros de pH y temperatura. Los MMDCL de G. Zhu et al. [50], son los más complejos, por asociar parámetros de calidad en tres diferentes componentes, donde cada uno de los componentes y combinados entre sí desarrollan MMDCL.
CONCLUSIONES
Las Plantas de tratamiento de agua potable son una parte esencial de la infraestructura de nuestra comunidad, cumplen un rol social y desempeñan un papel importante en la mejora de la calidad de vida mediante el tratamiento de aguas de los ríos, los cuales muchas veces son receptores de aguas residuales municipales e industriales.
Un modelo de predicción de la demanda de cloro es una herramienta útil que puede ayudar a los operadores de los servicios de agua potable a anticipar eventos de contaminación, optimizar el uso del cloro y tomar decisiones informadas y oportunas.
Este artículo examinó el rendimiento de 16 modelos matemáticos para predecir la demanda de cloro en aguas de río, a partir de la revisión de 04 artículos científicos. Si bien los MMDCL propuestos, coincidieron en algunas variables independientes, prevaleció las diferencias en todo el contexto de sus comp0nentes, lo cual es lógico, puesto que los modelos matemáticos son representaciones de los procesos físicos, químicos y biológicos que acontecen en una zona de estudio en particular.
Quince de los MMDCL propuestos por los autores fueron consistentes, con poder estadístico de predicción, con valor de R2 que estuvo entre 0.71 - 0.99; el MMDCL de G. Zhu et al. [50], con la variable explicativa fracciones de fluorescencia de materia orgánica tuvo un R2 de 0.41, lo que significa que es un modelo de bajo potencial predictivo.
La presente revisión ha dado lugar a tres contribuciones principales respecto a los MMDCL en agua de río: i) las ecuaciones de predicción con variables independientes de pH, temperatura, NH4, y materia orgánica expresada en diferentes parámetros sustitutos, pueden ser modelos matemáticos con alto poder estadístico de predicción de la demanda de cloro, ii) La heterogeneidad del rendimiento de predicción de los MMDCL pasa a convertirse en el principal objetivo del meta-análisis, porque la naturaleza de la formulación del modelo se explica por la combinación de los parámetros de calidad que caracterizan el grado de contaminación del recurso hídrico y iii) el SUVA y las fracciones fluorescentes de materia orgánica por sí solos no son buenas variables explicativas de la demanda de cloro, por lo que deben sumarse otras variables explicativas que contribuyan al rigor predictivo del modelo.
La presente revisión identificó algunas limitaciones de la aplicación de los modelos: i) ausencia de un procedimiento metodológico definido para el modelamiento de la demanda de cloro, ii) los MMDCL propuestos no consideraron la métrica R2 ajustada, que a diferencia de R2 advierte la cantidad de predictores y de datos disponibles, castigando la suma de predictores que no ajustan significativamente la capacidad de predicción del modelos, iii) los autores no profundizan bajo qué escenarios de calidad del recurso hídrico se construyeron los MMDCL.
La combinación de las variables que fueron utilizadas por los autores para la formulación de los MMDCL, expresan la inquietud por comprender e interpretar la influencia de los contaminantes que varían en el tiempo y en el espacio y su reacción con el cloro. Finalmente, se señala que el estudio del modelamiento de la demanda de cloro en agua de río como fuente de abastecimiento de agua potable es un campo por explorar, dado los pocos estudios realizados al respecto.