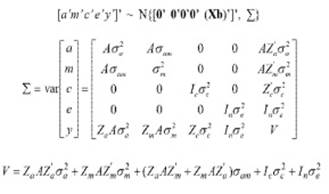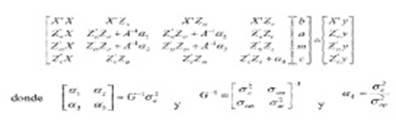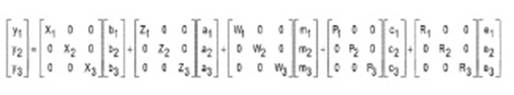INTRODUCCIÓN
El ganado Costeño con Cuernos (CCC) es una raza Bos taurus proveniente de cruces de animales traídos al continente americano durante la época de conquista, los cuales se han venido adaptando a las condiciones del trópico bajo colombiano (Ossa et al., 2011). El ganado CCC tiene promedios para peso al nacimiento de 29.3 kg, lo que contribuye con la facilidad de parto en esta raza. El promedio de peso al destete a los 8 meses es de 173.3 kg, con una ganancia de peso predestete de 609 g/día, y ganancia de peso posdestete a 16 meses de 229 g/día. Presenta una edad al primer parto de 37.6 meses, natalidad de 74.6% e intervalo entre partos de 14.1 meses. En hatos de CCC puro se observaron lactancias de 266 días con una producción de 1202 kg de leche (Ossa et al., 2011).
La eficiencia productiva y reproductiva del ganado CCC tiene un gran potencial de ser incrementada, dado que muchos de los núcleos de ganado evaluados corresponden a bancos de germoplasma que han tenido por objetivo mantener la variabilidad genética de esta raza, sin hacer una selección particular por características productivas. Una forma de incrementar la productividad en los sistemas de producción que utilizan CCC es mediante la implementación de un programa de mejoramiento genético. Para ello, es necesario disponer de un adecuado sistema de control de registros para rasgos de interés económico que estén altamente correlacionados con los objetivos de selección. Esto permite hacer estimaciones de valores genéticos con altos niveles de exactitud y así aumentar la tasa de ganancia genética producto del programa de mejora (Van Vleck et al., 1987).
Hoy día se tienen numerosos resultados disponibles en la literatura sobre parámetros genéticos en animales de carne que pueden servir de guía para un programa de selección (Domínguez et al., 2003; Ossa et al., 2007; Ríos 2008). Sin embargo, en el plano técnico, tales parámetros deben ser solo aplicables a la población y periodo de tiempo donde se estimaron. En el caso de animales criollos de Colombia, los resultados publicados muestran muchas variaciones; lo cual puede deberse a la estructura de los registros utilizados o al uso de modelos unicarácter que no extraen toda la información disponible en los datos (Ossa y Pérez, 2002; Gallego et al., 2006; Ossa et al., 2014; Martínez 2009).
Los análisis multicarácter mediante el modelo animal se recomiendan para hacer evaluaciones genéticas, porque realizan la evaluación simultánea de animales para dos o más características, y tienen en cuenta las correlaciones entre ellas (Henderson, 1976). Esto puede beneficiar el análisis al mejorar la exactitud de la evaluación y la respuesta a la selección. Con base a esto, el objetivo de este estudio fue: estimar los componentes de y parámetros genéticos en las variables peso al nacer, al destete y a los 16 meses del ganado CCC, mediante modelos unicarácter y multicarácter, para determinar sus ventajas al desarrollar un programa de mejora genética.
MATERIALES Y MÉTODOS
Los datos utilizados corresponden a registros productivos del Banco de Germoplasma de la raza bovina CCC, obtenidos entre los años 1989 a 2011. Estos animales se encontraban en el centro de investigación Turipaná de la Corporación Colombiana de InvestigaciónAgropecuaria (Agrosavia), ubicado en el Valle del Sinú (departamento de Córdoba), al nordeste de Colombia, a una altitud de 14 msnm. Este lugar se encuentra en la región Caribe, en una zona agroecológica que presenta una temperatura promedio de 28 °C, humedad relativa de 79-84% y una precipitación anual de 1200 mm, de los cuales aproximadamente el 80% caen entre los meses de mayo a noviembre.
Los animales fueron alimentados con una base forrajera que incluía predominantemente pasto Angleton (Dichantium aristatus) y pasto Guinea Tanzania (Megathyrsus maximus). En la época seca, la alimentación de las vacas paridas y aquellas próximas a parir fue complementada con ensilaje de maíz. Durante todo el año se suministró agua a voluntad y sal mineralizada. Los terneros fueron destetados a los 240 días de edad y el peso se registró al destete y a los 16 meses de edad.
La estructura de pedigrí fue conformada a partir de 3363 animales que contaban con datos, así como también por sus antecesores que no tenían registros propios (Cuadro 1). El modelo incluyó los efectos de año de nacimiento (1989 a 2011), época de nacimiento, sexo y número de parto. La época de nacimiento se agrupó de acuerdo con el mes de nacimiento: épocas 1, 2, 3 y 4 = nacidos en enero, febrero, marzo, y abril, respectivamente, y en la época 5 se incluyeron los nacidos entre mayo y diciembre (correspondiente a gestaciones ocurridas fuera de la estación de monta, en época de lluvia). El número de partos se conformó en siete clases, correspondientes las primeras seis con el orden de parto y la última donde se agruparon las de 7 y más partos. Los registros con datos por encima de tres desviaciones estándar con relación a la media fueron descartados; asimismo, se eliminaron aquellos grupos de contemporáneos (año-época-sexo de la cría) con menos de cinco observaciones.
Cuadro1. Estructura de la población de ganado Costeño con Cuernos (CCC) evaluada para el peso al nacer (PN), peso al destete (PD) y peso a los 16 meses (P16)
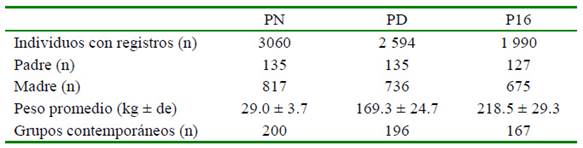
de = desviación estándar
En el modelo para el análisis de las variables peso al nacer (PN), peso al destete (PD) y peso a los 16 meses de edad (P16) fueron incluidos los efectos fijos de año, época de nacimiento, sexo y número de parto. Se implementó el procedimiento GLM del programa SAS 9.1.3. Los componentes de (co) varianza y los parámetros genéticos fueron estimados mediante modelos unicarácter y multicarácter utilizando el programa ASReml 3 de Gilmour et al. (2009).
Bajo el análisis unicarácter se implementaron seis modelos que tuvieron los mismos efectos fijos, pero con variación en sus efectos aleatorios. De esta manera, la importancia de los efectos aleatorios se estimó mediante la inclusión o exclusión de cada uno de los efectos del modelo animal. El modelo 1 incluyó efectos genéticos aditivos como único efecto aleatorio. El modelo 2 incluyó el efecto aditivo directo y el de ambiente permanente materno. El modelo 3 tuvo en cuenta el efecto aditivo directo más el efecto genético materno y asumió una covarianza igual a cero entre los efectos directos y maternos. El modelo 4 fue igual al modelo 3, pero asumió una covarianza diferente de cero entre los efectos directos y maternos. Los modelos 5 y 6 fueron iguales a los modelos 3 y 4, respectivamente, pero incluyeron el efecto de ambiente permanente materno.
De forma matricial, el modelo más completo (modelo 6) se describe como: y= Xb+ Z1a+Z2m+Z3c+e [Covarianza (a,m)‘«0], donde y es el vector de observaciones para la variable fenotípica; b es el vector de los efectos fijos que incluye los grupos de contemporáneos para PN y PD (año y época de parto), el sexo del animal (2 niveles), el número del parto de la madre (7 niveles); para P16 (año - época y sexo de la cría) y la edad del individuo como covariable lineal y cuadrática para el carácter respectivo (PD y P16); a es el vector de los efectos aleatorios genético aditivos directos; m es el vector de los efectos aleatorios genético aditivos maternos; c es el vector de los efectos aleatorios del ambiente permanente materno; e es el vector de los efectos aleatorios residuales; X, Z 1 , Z 2 , Z 3 son las matrices de incidencia, que relacionan las observaciones en y con b, a, m y c, respectivamente.
Las distribuciones de los efectos aleatorios del modelo fueron:
donde: σ2 es la varianza de los efectos aditivos directos; σ2 m es la varianza de los efectos aditivos maternos; σ2 c es la varianza de los efectos del ambiente permanente materno; σm es la covarianza entre los efectos aditivos directos y maternos; σ2 e es la varianza de los efectos residuales; A es la matriz de relaciones aditivas entre todos los individuos; I es la matriz de identidad.
Las ecuaciones del modelo mixto son:
Se seleccionaron los modelos con mayor valor de logL y menores criterios de información de Akaike (AIC) y de información Bayesiana (BIC). En esta prueba (PRV), los grados de libertad de la distribución de Chi cuadrado tiene igual número de parámetros en el modelo completo menos el número de parámetros en el modelo reducido.
Para el análisis multicarácter se emplearon los mismos datos y se evaluaron solamente los modelos unicarácter de mejor bondad de ajustes previamente identificados.
La representación general del modelo multicarácter fue:
donde: yi es un vector de n x ij de n registros y jth caracteres analizados simultáneamente en cada i animal; b es el vector de efectos fijos de grupos de contemporáneos para PN y PD (año -época de parto), número de parto (7 niveles), sexo (2 niveles), para P16 (año -época de parto -sexo) y las covariables cuadráticas de edad al destete y edad a los 16 meses para la característica correspondiente. a es el vector de efectos aleatorios genéticos aditivos directos; m es el vector de efectos aleatorios genético aditivo materno; c es el vector de efectos aleatorios maternos de ambiente permanente; ej es un efectoaleatorioresidual correlacionadoparalos tres rasgos; X i Z i , W i y R i, son matrices de incidencia que relacionan los efectos fijos y aleatorios con el vector de datos. En este modelo se asume que:
donde σ2 ai;σ2 mi ;σ2 ci;σ2 ei,σa12,σm12,σw12 y σe12 representan las varianzas para efectos genéticos directos, maternos, de ambiente permanente, residual, covarianza entre efectos genéticos directo, materno, de ambiente permanente y residual respectivamente. A es la matriz de parentesco entre todos los animales; Ic e In son matrices de incidencia de los efectos permanente maternos y residual respectivamente y ( es el símbolo de producto. La heredabilidad para los efectos aditivos (h2 a), efecto materno (h2 m) y total (h2 T), las correlaciones genéticas entre los efectos directos y maternos (ram); las correlaciones genéticas entre los rasgos para efectos directos (ra) y maternos (rm) se calcularon según las siguientes fórmulas:
La magnitud de los valores de h 2 sirvió como criterio para comparar los resultados de los análisis unicarácter y multicarácter. Las soluciones de ambos modelos para el efecto genético directo y materno proporcionaron los Valores Genéticos (VG) de cada animal. La precisión (acc) fue estimada por:
donde: PEV es el error de predicción del VG para el ith rasgo con varianza σ2 ai.
RESULTADOS Y DISCUSIÓN
Estimación de Componentes de (co) varianza para Pesos, Mediante Modelo Unicarácter
En general, los resultados de logL, AIC y BIC presentaron una alta variación. Los modelos con mayor número de pará-metros pueden ser los de mejor ajuste según logL. Sin embargo, los criterios informativos AIC y BIC, que penalizan por estas diferencias, presentaron algunas divergencias. El Cuadro 2 muestra que las diferencias entre p de los seis modelos oscilaron entre 1 y 3 para un nivel significativo de 0.05%, mientras que el Chi cuadrado expresó valores entre 3.8 y 7.8. De acuerdo con estos resultados, se puede indicar que respecto al modelo 1, con efectos genéticos aditivos como único efecto aleatorio, la inclusión de otros efectos aleatorios mejoró el ajuste del modelo para todos los rasgos, excepto para P16.
Cuadro 2 Resultados de los criterios de información de los modelos comparados respecto a logL AIC y BIC del modelo 1
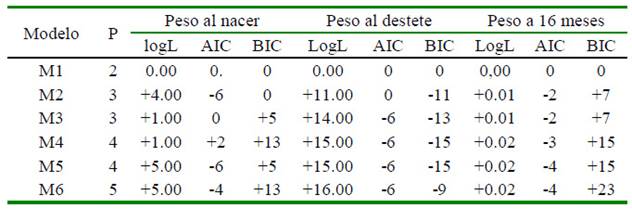
Para PN, la inclusión de los efectos genéticos directos y maternos (modelo 3) o la consideración de la covarianza entre ambos efectos genéticos (modelos 4 y 6) no mejoraron los ajustes respecto al modelo 2. Por su parte, el modelo 5 no difiere del modelo 2 usando logL y AIC, pero la mayor penalización aplicada por el BIC sugiere que es el modelo 2 el de mejor ajuste para este rasgo.
Para PD, los modelos 3 al 6 no presentaron grandes diferencias cuando se consideraron los tres criterios comparativos, y ajustaron mejor los datos respecto al modelo 1. Los modelos que asumieron una covarianza no nula entre efectos genéticos directo y maternos (modelos 4 y 6) no difieren entre sí, ni tampoco con el modelo 5 que la excluye. El modelo 2 no manifiesta diferencias con el resto de los modelos y es mucho más simple.
El P16 manifestó uniformidad y ningún modelo fue mejor que el modelo 1, el cual solo incluye efectos genéticos directos. La generalización de esta comparación indicó que no existieron diferencias entre los modelos 2 y 5, y cualquiera de ellos fueron los de mejor ajuste a los datos de PN y PD, mientras para P16 cualquiera de ellos puede aplicarse.
En el presente estudio se hizo particular énfasis en la discusión de los resultados obtenidos con los modelos 2 y 5, lo que facilitó el análisis multicarácter, al asumir nula la covarianza entre efectos directos y maternos. Según Gallegos et al. (2011), la incertidumbre para estimar con precisión la covarianza entre los efectos genéticos directos y maternos, es la razón por la cual 13 de 20 asociaciones de ganaderos de bovinos de carne en EEUU utilizaron un valor de cero para esta covarianza en las evaluaciones genéticas nacionales (BIF, 2010). Esto concuerda con Domínguez et al. (2009), quienes indican que la definición de modelos debe ser previa a las evaluaciones genéticas, y depende de la información disponible y su estructura, especialmente cuando esta es limitada y cuando el uso de modelos complejos dificulta estimar componentes de (co)varianza con precisión.
Los modelos 2 y 5 tienen en cuenta los efectos maternos. Para Meyer (1992), Ríos (2008) y Martínez (2009), la no inclusión de alguno de estos efectos generará una sobrestimación del componente genético aditivo directo. Los componentes de varianza y parámetros genéticos estimados para los modelos 2 y 5 se muestran en el Cuadro 3, observándose que la heredabilidad de los efectos directos fue más alta que la estimada para los efectos maternos. En general, las h2 a para los tres caracteres fueron bajos según la clasificación de Preston y Willis (1974), lo que sugiere que la varianza fenotípica total está más influida por efectos ambientales y genéticos no aditivos. Los valores de hereda-bilidad materna para el peso al nacer sugieren que es muy poco el efecto materno.
Cuadro 3 Componentes de varianza y parámetros genéticos del peso vivo (kg) a tres edades en Costeño con Cuernos (modelos unicarácter 5 y 2)
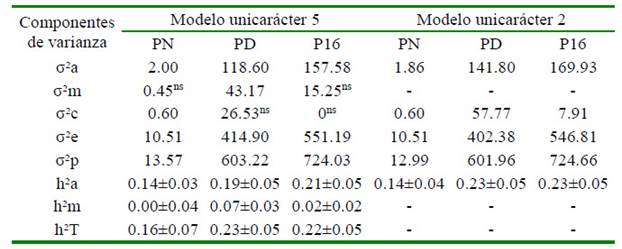
PN: Peso al nacimiento; PD: Peso al destete; P16: Peso a los 16 meses
σ2a= varianza genética aditiva directa; σ2m = varianza genética aditiva materna; σ2c= varianza de efectos ambientales permanente; σ2e = varianza del error; σ2p = varianza fenotípica total; h2a = heredabilidad efectos directos; h2m = heredabilidad efectos maternos; h2T = heredabilidad total
Para el PN, en ganado CCC, Martínez et al. (2006) y Ossa et al. (2008) informaron valores superiores para la heredabilidad directa (0.17±0.0 y 0.28±0.05) a los encontrados en el presente trabajo, y cercanos a los de heredabilidad materna (0.012±0.003 y 0.081±0.030, respectivamente). Valores inferiores para la heredabilidad directa para PN (0.12±0.07) fueron encontrados por Domínguez et al. (2003) y superiores por Gallego et al. (2006),Assan (2012) y Ndofor et al. (2012) y Martínez et al. (2018) con valores de 0.38±0.017, 0.25±0.003, 0.39 y 0.19, respectivamente. Respecto a la heredabilidad materna, en otros estudios (Gallegos et al., 2011; Assan, 2012; Ndofor et al., 2012) encontraron valores superiores (0.03, 0.10 y 0.17, respectivamente) al encontrado en este estudio
Los valores de heredabilidad directa y materna para el PD indicaron que en el componente genético influye la habilidad que tienen las crías para su propio crecimiento y la de las madres para criar un ternero. La heredabilidad directa que se estimó es cercana a la encontrada por Martínez et al., (2006) en ganado CCC (0.210 ± 0.074), y por Martínez et al. (2018) en ganado Romosinuano (0.21±0.12), así como en otras razas por Caires et al. (2009) y Martínez (2009) (0.19±0.07 y 0.18-0.45, respectivamente). Valores superiores fueron encontrados por Ndofor et al. (2012) y Caires et al. (2009) (0.25-0.35). En el presente estudio se encontró una heredabilidad materna del PD similar a la encontrada por Martínez et al. (2006), Gallego et al. (2006) y Ossa et al. (2008) (0.05±0.038 para ganado CCC, 0.05±0.025 para Blanco Orejinegro y 0.06±0.01 para Cebú Cubano, respectivamente). Valores superiores fueron descritas por Ribeiro et al. (2009) y Eaglen et al. (2013) (0.18-0.20).
Al igual que el peso al destete, la h2 a para P16 meses está muy influenciada por la alimentación y el manejo brindado a los animales. En la heredabilidad directa para P16 meses se obtuvieron estimaciones inferiores a las de este estudio por Gallego et al. (2006) y Martínez et al. (2009) en ganado Blanco Orejinegro (0.09) y Sanmartinero (0.14), respectivamente.Asimismo, valores superiores fueron reportados por Assan (2012) y Caires et al. (2009) de 0.24±0.07 y 0.09-0.63, respectivamente.
Estimación de Componentes de (co)varianza para Pesos, Mediante Modelo Multicarácter
El Cuadro 4 presenta los valores de los componentes de (co)varianza y los estimadores de parámetros para las características PN, PD y P16 en bovinos CCC, obtenidos a través de análisis multicarácter según modelos 2 y 5. Similar a los resultados del modelo unicarácter, los efectos genéticos, así como de ambiente permanente materno, no fueron significativos en dos de tres caracteres analizados por el modelo 5. Por el contrario, los resultados del modelo 2 multicarácter y unicarácter fueron muy similares.
Cuadro 4 Componentes de varianza y parámetros genéticos del peso vivo (kg) a tres edades en ganado Costeño con Cuernos (modelos multicarácter 5 y 2)
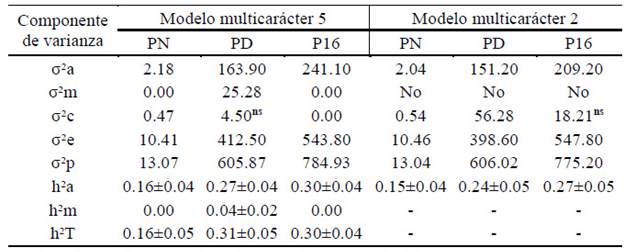
PN: Peso al nacimiento; PD: Peso al destete; P16: Peso a los 16 meses
σ2a= varianza genética aditiva directa; σ2m = varianza genética aditiva materna; σ2c= varianza de efectos ambientales permanente; σ2e = varianza del error; σ2p = varianza fenotípica total; h2a = heredabilidad efectos directos; h2m = heredabilidad efectos maternos; h2T = heredabilidad total
Al comparar los componentes de varianza genéticos para cada carácter estimados por modelo unicarácter y multicarácter (Cuadros 3 y 4), se presentó un incremento entre 9 y 50% en la varianza genética directa en el modelo 5, mientras que estos aumentos fueron del 9 al 23% en el modelo 2. Dado que la varianza fenotípica total se mantuvo prácticamente sin cambios en ambos procedimientos, consecuentemente los estimados de heredabilidad presentaron un incremento en los modelos multicarácter. Lo anterior es de esperarse ya que los modelos multicarácter se benefician de las covarianzas genéticas entre los caracteres involucrados (Mrode, 1996).Al respecto, Thompson y Meyer (1986) plantearon que cuando los datos provienen de poblaciones con selección de caracteres correlacionados genéticamente, los análisis unicarácter pueden estar sesgados, mientras que con los análisis multicarácter se puede reducir el sesgo.
Al comparar la magnitud de los valores de la heredabilidad de los resultados de los análisis unicarácter y multicarácter, se observó una similitud para la variable peso al nacer de 0.14 y 0.16 respectivamente; mientras que para peso al destete, en el modelo 5 se observa una ligera ventaja del análisis multicarácter, donde la h2 a se incrementa 42%, al pasar de 0.19 en el análisis unicarácter a 0.27 en el multicarácter. Igualmente, la h2 T se incrementa 34% (de 0.23 a 0.31). Similar situación ocurrió para el peso a 16 meses, donde hubo un incremento para h2 a de 0.21 a 0.30, que equivale a 42%. Para el modelo 2, el rasgo que presentó mayor incremento (17%) de la h2 a fue el peso a 16 meses al aumentarse de 0.23 a 0.27.
La heredabilidad para el efecto directo del peso al destete del modelo 5 multicarácter es similar al promedio reportado por Domínguez et al. (2009), en una revisión donde hace referencia a un valor medio no ponderado de 0.27 para la h2 a del PD en todas las razas de bovinos de carne estudiadas. En general, la h2 a estimada para el P16 y la varianza genética aditiva directa sugieren que en la población estudiada existe suficiente variabilidad genética para el mejoramiento de dicho rasgo, con base en la selección de los animales superiores. La h2 a del P16 se incrementó con respecto al PD. Esta tendencia es similar, aunque con heredabilidades de menor magnitud a las descritas en bovinos Tabapúa (Sousa et al., 2010) y Nelore (Albuquerque y El Faro, 2008).
Estimadores de Correlaciones Genéticas y Fenotípicas entre Pesos
Los valores de correlaciones genéticas y fenotípicas para las tres características (PN, PD, P16) en los modelos 2 y 5 presentaron valores muy similares. La correlación genética entre el peso al nacer y el peso al destete para los modelos 2 y 5, fueron altas y positivas (Cuadro 5), lo que podría indicar que algunos de los genes que actúan para el peso al nacer intervienen en el peso al destete.
Cuadro 5 Correlaciones genéticas y fenotípicas entre las características de crecimiento en ganado criollo Costeño Con Cuernos, estimadas por dos modelos multicarácter (Por encima de la diagonal las correlaciones genéticas y por debajo de la diagonal las correlaciones fenotípicas)
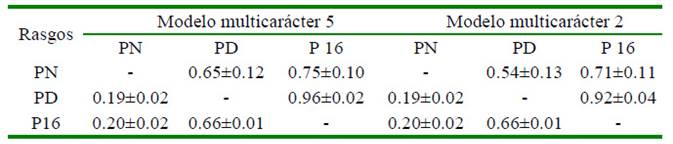
PN: Peso al nacimiento; PD: Peso al destete; P16: Peso a los 16 meses
Valores bajos y positivos (0.21 y 0.16) fueron hallados por Martínez et al. (2006) en esta misma raza (CCC) y Ossa et al. (2007) en Romosinuano.
De igual manera, en ambos modelos (2 y 5), la correlación genética entre el peso al nacer y el peso a 16 meses fue alta y positiva, aunque más elevada que la encontrada entre el peso al nacer y el peso al destete, lo cual es quizás consecuencia del efecto materno, que tuvo una mayor influencia sobre el peso al destete y muy poca sobre el peso al nacer y el peso a los 16 meses de edad. Estos resultados son contrarios a los referidos por Ossa et al. (2007), quienes encontraron correlaciones nulas entre el peso al nacer y peso a los 16 meses de edad, en ganado criollo Romosinuano.
La correlación genética entre el peso al destete y el peso a 16 meses (modelos 2 y 5) fue alta y positiva, y señala que estos dos caracteres manifiestan una base genética común; de manera que un proceso de selección sobre el peso al destete produciría un aumento en el peso a los 16 meses. Similares tendencias fueron publicadas por Gallego et al. (2006) y Ossa et al. (2007) en las razas criollas colombianas, Blanco Oreginegro y Romosinuano, respectivamente.
La correlación fenotípica entre peso al nacer y los pesos al destete fueron de 0.19 y 0.20, respectivamente (Cuadro 5), valores que son considerados bajos, pero positivos, lo que indica una baja determinación de un rasgo precedente en el siguiente. Resultados similares fueron hallados por Ossa et al. (2007) para la raza Romosinuano.
En ambos modelos 2 y 5, las correlaciones fenotípicas entre PD y P16 fueron de 0.66, considerada como positiva alta. Como las causas genéticas y ambientales se combinan para dar la correlación fenotípica y ambos caracteres tienen baja heredabilidad, entonces la relación está dada principalmente por la correlación ambiental. Este resultado es similar al hallado por Ossa et al. (2007) enganado criolloRomosinuano,perodifieredel resultado de Martins et al. (2000), quiénes informaron una correlación nula entre el peso al destete y el peso a los 500 días de edad.
Los modelos de rasgos múltiples redujeron el sesgo introducido por la selección secuencial y permiten obtener estimadores de las correlaciones genéticas y fenotípicas, con el beneficio de cuantificar las respuestas a la selección (Ramirez-Valverde et al., 2007). Se espera que las ventajas potenciales de la implementación de modelos animales de rasgos múltiples se muestren en el momento de la selección y, para esto, es necesario evaluar las correlaciones entre la BV estimada por ambos procedimientos.
Las variaciones entre VG fueron superiores para el procedimiento multicarácter respecto al unicarácter. Esta mayor variabilidad fue de 8.1% para PN, 12.9% para PD y solo 3.7% para P16. Las correlaciones entre los VG estimados por ambos procedimientos fueron superiores a 0.945, lo cual indicó que sería válido seleccionar los mismos animales cualquiera sea el modelo aplicado; en otras palabras, no existirían cambios en el orden de mérito. La otra ventaja de los modelos multicarácter está en el incremento de la precisión de los VG estimados, y este indicador es una de las mejores herramientas disponibles para maximizar la respuesta al programa de selección (Mokhtari y Rashidi, 2010). Dicho incremento es particularmente importante cuando se puede obtener con los mismos datos disponibles y sin grandes gastos adicionales, excepto los dedicados al servicio de computación.
Otros estudios también mostraron ventajas al implementar análisis de rasgos múltiples para rasgos de crecimiento en poblaciones de ganado vacuno debido al aumento de los estimadores de heredabilidad y la mejora de la precisión de los valores estimados de reproducción (Ramírez-Valverde et al., 2007).
El Cuadro 6 presenta los estimados de precisión de los valores genéticos para los tres rasgosevaluados.Estosresultadosindicaronque cualquiera sea el modelo o el rasgo analizado, el procedimiento multicarácter proporcionó un aumento en la precisión de los VG entre 4.3 y 15.8%. La precisión del VG estimado, según el modelo 5, siempre fue superior al modelo 2 cuando se aplicó un análisis multicarácter. Cuando se utilizaron modelos unicarácter esta tendencia sólo se cumplió para PN.
Cuadro 6 Precisión de los Valores Genéticos (VG) para los rasgos de crecimiento según los modelos utilizados
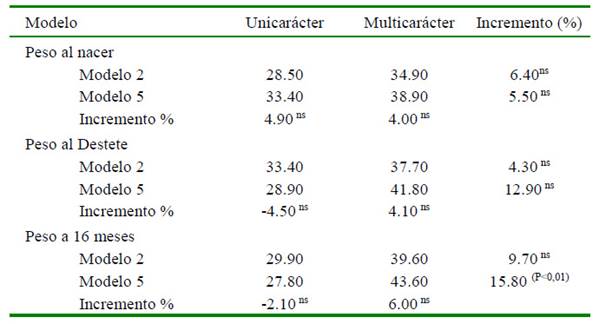
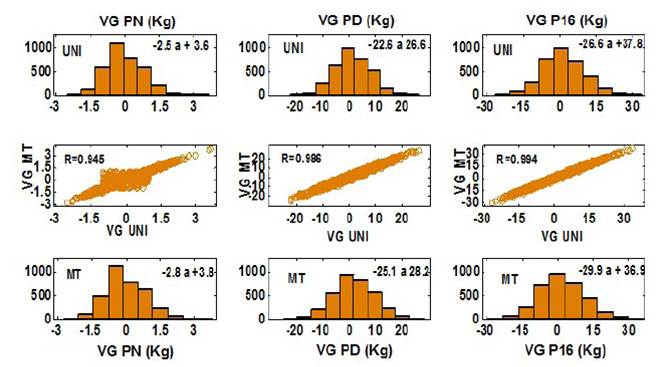
Figura 1 Distribución de frecuencias y correlación entre los valores genéticos estimados según modelos unicarácter (UNI) y multicarácter (MT) en ganado Costeño Con Cuernos
La implementación exitosa de modelos multicarácter depende en gran medida de la cantidad y estructura de los datos. En el presente estudio, se logró convergencia para todos los modelos evaluados, a pesar de los diversos componentes de (co) varianza que se estimaron y la reducida información, lo cual fue compensado quizás por la estructura equilibrada de la base datos.
CONCLUSIONES
Los valores de heredabilidad y correlaciones genéticas para los peso al nacer, peso al destete y peso a los 16 meses de edad están dentro de lo informado en las publicaciones disponibles y deben interpretarse como la caracterización gené-tica de la raza criolla Costeño Con Cuernos.
El uso de los modelos multicarácter presentó ventajas respecto al procedimiento unicarácter, particularmente en una mayor precisión del valor genético en el peso a los 16 meses.











 uBio
uBio