Encaminar a los niños que presentan dificultad para aprender es una de las cuestiones más importantes que enfrentan los docentes en su quehacer cotidiano. En los procesos iniciales de acercamiento a la escuela este problema es particularmente acuciante porque el desarrollo de ciertas competencias básicas puede determinar oportunidades o desafíos para la formación avanzada de los aprendices.
En el caso de la educación matemática, la enseñanza de las operaciones de adición y sustracción forma parte del contenido curricular en los primeros años de educación formal, porque capacita a los individuos con conocimientos que soportan la adquisición de otros (Bonilla et al., 1999; Fritz et al., 2013). Debido a su relevancia social, la actividad del maestro en el marco de la enculturación matemática formal, que tiene como finalidad “iniciar a los niños en las simbolizaciones, las conceptualizaciones y los valores de la cultura matemática” (Bishop, 1999, p. 120), se convierte en uno de los principales ejes de análisis en el ámbito educativo.
La enseñanza es una forma de actividad que supone un alto grado de planeación porque exige a los maestros ajustar reflexivamente diversos componentes seleccionados para su labor a las necesidades específicas de los aprendices a quienes orienta (Castro, 2008). En sus esfuerzos, el maestro de matemáticas hace algo más que meramente escoger los contenidos o los ejercicios que presenta a los estudiantes en el aula; el docente establece la configuración del entorno de aprendizaje, los materiales y recursos con los que se llevan a cabo las prácticas, los puntos o vértices atencionales a los que los aprendices deben dirigirse, los estados y procesos psicológicos de los pupilos que han de ser influenciados o desarrollados por la labor conjunta (Godino et al., 2016; Radford, 2014).
Hay que tener en cuenta que los profesores realizan sus actividades de planeación sin desatender las exigencias que imponen las instituciones educativas a su labor. Dado que en diversas comunidades hay diferentes actores interesados en el aprendizaje, especialmente en los niveles iniciales, los docentes se involucran normalmente en una labor que exige habilidades para interactuar significativamente con los interesados, de modo que establecen un enlace entre las exigencias del medio social y las condiciones específicas del contexto educativo en el que se desempeñan (Kuriloff et al., 2019).
Esto implica que las concepciones individuales de las personas que ejercen la enseñanza son un antecedente directo que conecta los fines sociales del ámbito educativo con la experiencia cotidiana de aprendizaje en las instituciones educativas (Boyer y Mailloux, 2015; Llinares, 2018). A esta labor de conexión entre el saber socialmente acumulado y el contexto interactivo habitual de los principiantes se le conoce como “mediación”, así, el docente es un agente que media de manera consciente, reflexiva y deliberada en la adquisición de saberes, adaptando el conocimiento científico y disciplinar a situaciones cotidianas en las que el neófito puede contar con su apoyo (Boyer y Mailloux, 2015; Carlsen et al., 2016)
En ese sentido, la conexión entre la actividad mediacional de quien enseña y la experiencia de aprendizaje de los educandos se comprende mejor desde un enfoque psicopedagógico que considere las situaciones de interacción de las personas entre ellas y con el ambiente físico en prácticas socio-culturales regulares. A esta forma de abordaje se le conoce actualmente como cognición situada (Cobb y Bowers, 1999; Rhoads y Weber, 2016; Robbins y Aydede, 2009) y supone que: a) Los fenómenos psicológicos emergen en la interacción social entre personas que coinciden espacio-temporalmente; b) El conocimiento se expresa en ambientes socialmente significativos; y c) Hay un trasfondo de la interacción que orienta normativa pero implícitamente las actividades de las personas de manera tal que su comportamiento se ajusta a la tradición cultural en la que viven (Ramstead et al., 2016; Rietveld y Kiverstein, 2014).
Adoptar esta postura teórica no solo es cuestión de afinidad con las tendencias de pensamiento más actuales en psicología y pedagogía, sino que siguiendo ideas de este enfoque se han realizado estudios en los que se ha observado que los niños aprenden mejor aritmética en situaciones que están profundamente interrelacionadas con el resto de su vida cotidiana (Baroody, 2017; Clarke y Roche, 2018). Además, se han evidenciado efectos del desarrollo profesional del docente sobre el logro académico del estudiante (Prast et al., 2018) y se han propuesto nuevas alternativas pedagógicas que mejoran las capacidades del profesor al interactuar con los niños (Nousiainen et al., 2018; Sullivan, 2018). De otra parte, se han realizado propuestas inclusivas para tener en cuenta las diferencias de aprendizaje de los estudiantes adaptando la actividad del docente (Moscardini, 2014; Roose et al., 2019).
Más aún, se ha sugerido que las ideas de los docentes acerca de cómo piensan sus estudiantes son información valiosa para orientar las prácticas conjuntas facilitando la aplicación de una estrategia holista que conduce al desarrollo de competencias para la comprensión y el aprendizaje profundos (Ramli et al., 2013). Esta observación es altamente recurrente como tema central en la historia de la psicología del aprendizaje. Un ejemplo de lo anterior es la formulación de la competencia Mirar profesionalmente el pensamiento matemático de los niños (Jacobs et al., 2010). Los autores conceptualizan esta experticia como “un conjunto de tres habilidades interrelacionadas: atender a las estrategias de los niños, interpretar las comprensiones de los niños y decidir cómo responder sobre la base de dichas comprensiones” (p. 72).
Las tendencias de pensamiento derivadas del trabajo de Vygotsky siempre han enfatizado la importancia de la actividad mediacional para comprender el avance intelectual que conduce al desarrollo (Montealegre, 2005, 2007). Hay que destacar que no hay una brecha insalvable entre las concepciones situadas del aprendizaje y la psicología histórico cultural que sigue los lineamientos trazados por Vygotsky, en ambos casos: a) La interacción social es el eje articulador del aprendizaje, b) La actividad reflexiva del maestro es una condición de la adquisición de hábitos y competencias de los escolares y, c) Los objetos de aprendizaje juegan un rol central como depósitos accesibles de una tradición académica en la que se introduce al estudiante.
Ahora bien, es preciso notar que estos aspectos estructurales en la dinámica enseñanza-aprendizaje pueden exhibir facetas bastante diversas en comunidades educativas dispares. Más aún, a causa de los esfuerzos adaptativos que los docentes imprimen a su actividad planificadora en cada entorno escolar hay una gama más o menos amplia de potenciales divergencias que se pueden indagar.
El presente estudio pretende evaluar la actividad planificadora en dos naciones que comparten el interés por la regularización y estandarización de los contenidos (Perú y Colombia) como parte de su esfuerzo por mejorar los procesos educativos de cada sociedad. Existe un interés de los Estados en promover cierta convergencia de la enseñanza, donde el maestro es el agente que acondiciona los parámetros legales promovidos en su nación a las realidades específicas del aula.
En el caso de Perú y Colombia, la coincidencia de los estándares relacionados con el dominio de la adición y sustracción al finalizar segundo y tercer grado, dan cuenta del propósito común en ambas naciones de que el currículo fomente ciertas competencias comúnmente evaluadas en las pruebas, esta tendencia se evidencia en sus documentos guía:
Perú: Resuelve problemas referidos a acciones de juntar, separar, agregar, quitar, igualar y comparar cantidades; y las traduce a expresiones de adición y sustracción (Ministerio de Educación, 2016, p. 75).
Colombia: Resuelvo y formulo problemas en situaciones aditivas de composición y de transformación (Ministerio de Educación Nacional, 2006, p. 35).
En ese sentido, el ejercicio comparado que se desarrolla en este trabajo es valioso porque brinda un modo de acceso a la configuración de las prácticas educativas y al sentido en que las interacciones interpersonales que fomentan el aprendizaje pueden variar entre diferentes comunidades. Además, analizar la diversidad en la planeación del aprendizaje brinda información valiosa sobre el modo en que la estandarización de los currículos y la aparición de criterios educativos nacionales e internacionales regularizan los contenidos de instrucción y las actividades de enseñanza (Valverde y Näslund-Hadley, 2010). Enfatizar la importancia de la heterogeneidad de los ambientes educativos mejora el entendimiento de los retos enfrentados por los docentes en comunidades educativas dispares.
Para promover la reflexión de los docentes y maximizar la pertinencia de los resultados en esta investigación se decidió que el docente debería reflexionar sobre la actividad de los estudiantes que, desde su punto de vista, tienen dificultad en adición y sustracción, es decir, aquellos individuos que normalmente tienen problemas para ajustarse a las exigencias que plantean los criterios de éxito en la educación formal. Se trata de niños en edad escolar cuyo nivel de competencia al resolver sumas y restas no cumple los mínimos planteados por los documentos guía de ambos países.
Este estudio enfatiza una aproximación situada porque supone que el conocimiento de los maestros y su reflexión sobre cómo lidiar con las dificultades experimentadas por sus estudiantes en el aula es una mejor fuente de información para mejorar la comprensión de los riesgos y oportunidades en cada entorno escolar.
El estudio busca conocer tres facetas del proceso de deliberación del docente en su rol de mediador del aprendizaje: a) La sensibilidad a las condiciones y necesidades del estudiante con dificultad, b) La manera de disponer actividades y experiencias que fomenten el aprendizaje y, c) La capacidad para instituir tareas con diversos niveles de complejidad, de manera tal que su quehacer docente promueva el aprendizaje. Estos aspectos enlazados pueden generar una descripción de los procesos reflexivos y metacognitivos del maestro como mediador de la actividad del infante.
Método
Población y muestra
En el estudio participaron 40 docentes, 20 peruanos y 20 colombianos, 6 hombres y 34 mujeres, con edades entre 24 y 59 años y con una trayectoria que va desde los 4 hasta los 35 años de experiencia docente. Del total de participantes, 9 enseñan en grado primero, 10 en grado segundo, 15 en grado tercero, 3 en grado cuarto y 3 en grado quinto.
Los docentes peruanos se contactaron a través de visita directa a instituciones educativas de Lima como parte de una pasantía de investigación realizada en 2017 por la primera autora. El grupo de docentes colombianos se conformó mediante cartas de invitación a participar en la investigación, dirigidas a rectores de instituciones educativas de Bogotá. Se trabajó con los docentes peruanos y colombianos que aceptaron participar en el estudio.
Instrumento
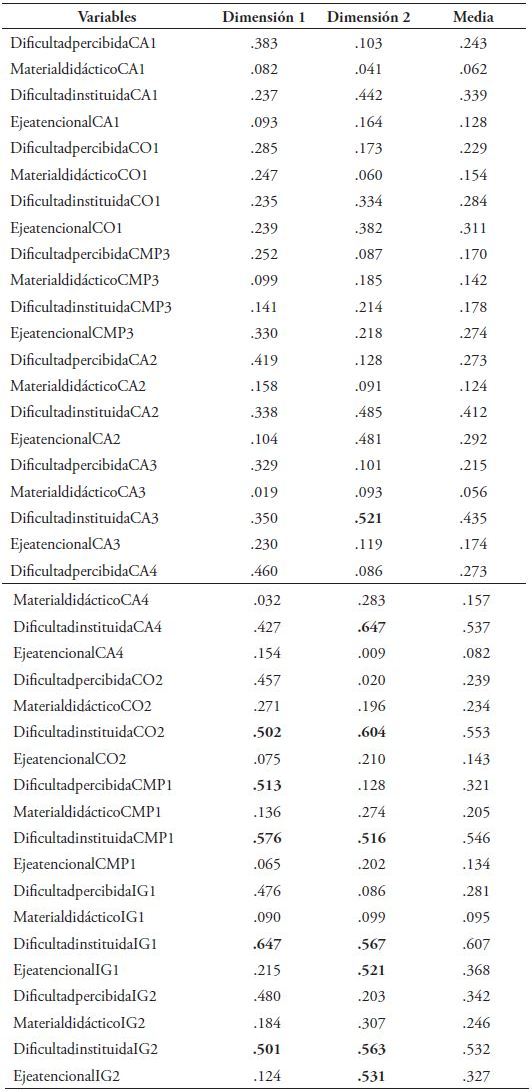
Se utilizó el Instrumento para Evaluación de Dificultad Instituida en Situaciones de Adición y Sustracción (DISAS) de Santana y Herrera (2017) que indaga en los docentes cómo enseñan diez situaciones de adición y sustracción a niños con dificultad en estas operaciones, situaciones que se discriminan así: cuatro de cambio (Cambio 1, Cambio 2, Cambio 3 y Cambio 4), dos de combinación (Combinación 1 y Combinación 2), dos de comparación (Comparación 1 y Comparación 3), y dos de igualación (Igualación 1 e Igualación 2), según la clasificación de Carpenter et al. (1981). Las características psicométricas del instrumento indican que es bastante confiable de manera global de acuerdo con el índice alfa de Cronbach (α = .73), y considerando las variables continuas evaluadas: Dificultad percibida, que se define como las apreciaciones del docente acerca de la dificultad que experimenta el estudiante en situaciones de adición y sustracción (α = .95); y Dificultad Instituida, que es el nivel de esfuerzo del aprendiz previsto por el docente para el logro del éxito en las actividades que ha diseñado para el aprendizaje de la adición y sustracción (α = .92).
En cuanto a evidencia de validez, los ítems de DISAS se sometieron a proceso de validez de contenido por juicio de expertos mediante agregados individuales, en las dimensiones de coherencia, claridad, relevancia y suficiencia. Asimismo, el instrumento se analizó en dos dimensiones: Evaluación de las relaciones entre el constructo y el contenido de la prueba, y evaluación de los factores contextuales internos y externos (Santana y Herrera, 2017).
Procedimiento de recogida y análisis de datos
El instrumento se aplicó a través de una interfaz interactiva compilada en el lenguaje de programación para experimentos psicológicos PEBL-2 (Mueller y Piper, 2014) La aplicación del instrumento se llevó a cabo de manera presencial e individual, teniendo en cuenta el protocolo de aplicación diseñado para DISAS por Santana y Herrera (2017), y se empleó para este estudio la base de datos de la validación del instrumento.
En cuanto a las facetas del proceso de deliberación del docente en su rol de mediador del aprendizaje, estas se midieron a través de las siguientes variables: La sensibilidad del docente a las condiciones y necesidades del estudiante con dificultad se obtuvo mediante un índice de dificultad percibida, en una escala de 1 a 5, donde 1 es que el docente considera que el estudiante percibe la tarea como “Muy fácil” y 5 como “Muy difícil”. Teniendo en cuenta que la dificultad puede analizarse desde un continuo de situaciones muy difíciles, donde el niño recién inicia su proceso de enculturación formal hasta situaciones muy fáciles en las que la progresiva participación y ajuste en prácticas matemáticas con su normatividad asociada se traduce en mayor dominio de las operaciones aritméticas, se procedió a la recodificación en la base de datos de la Variable dificultad percibida, donde 1 es “Muy difícil”, 2 es “Difícil, 3 es “Ni fácil ni difícil”, 4 es “Fácil” y 5 Muy fácil”.
La habilidad del docente al instituir tareas con diversos niveles de complejidad se evaluó a través de un índice de dificultad instituida, en el que se pregunta al docente el nivel de esfuerzo que le implicaría al educando la resolución de cada situación de adición y sustracción; se midió en una escala de 1 a 5, donde 1 es “Poco esfuerzo” y 5 “Mucho esfuerzo”.
La manera en la que el docente dispone de actividades y experiencias que fomenten el aprendizaje se evaluó a través de las variables categóricas: a) material didáctico, que interroga al docente sobre el material más propicio para la enseñanza de una situación aritmética particular y, b) eje atencional, que le pregunta al docente hacia dónde dirigir la atención del aprendiz, en una gradación que va de elementos concretos corporeizados a entidades abstractas.
La estrategia de análisis se realizó en tres fases. En primer lugar, se realizó prueba T para muestras independientes para analizar si existen diferencias por país en cuanto a la dificultad instituida y la dificultad percibida en los diez tipos de casos de aprendizaje de la suma y de la resta. Asimismo, se realizó el análisis de varianza (ANOVA) paramétrico de 1 factor para examinar si existen diferencias por grado en relación con la dificultad instituida y percibida.
Posteriormente se discretizaron las variables continuas de dificultad instituida y dificultad percibida, y se realizó un análisis de correspondencias múltiples (ACM) general bajo el método de normalización simétrico, para obtener un panorama cualitativo organizado de la reflexión docente. Se consideraron como variables activas la dificultad percibida, la dificultad instituida, el material didáctico y el eje atencional, y se dejó como variable ilustrativa el país.
Finalmente se segmentó la base de datos por país, y se hicieron análisis de correspondencias múltiples por país, para indagar a profundidad la naturaleza de las divergencias en la actividad mediacional; las cuatro variables ya descritas se seleccionaron en el análisis como variables activas. Los análisis estadísticos se realizaron en el programa SPSS 24.0.
Resultados
La prueba T para muestras independientes demostró que no hay diferencias significativas entre los docentes de ambos países con respecto a su percepción de la dificultad de los estudiantes ni con respecto a su tendencia a exigir cierto nivel de esfuerzo para resolver tareas de cambio, combinación, comparación e igualación. Este es un resultado esperado puesto que como se mencionó en la Introducción, las políticas públicas y tendencias pedagógicas en ambos países coinciden por efecto de la globalización sobre la política pública.
El análisis de varianza ANOVA de acuerdo con el grado en el que el docente enseña indica que hay diferencias significativas en los problemas de igualación (Dificultad Instituida Igualación 1 F ( 4,35 ) =3,031, p = .030), lo cual refleja un aumento de la exigencia de los docentes en los grados superiores, visible en este tipo de problemas porque se trata de tareas un poco más complejas que suponen la integración de situaciones de cambio y comparación (p. ej. 5 es menos que 16. ¿Cuánto debo agregarle a 5 para que sea igual a 16?).
Coincide con este análisis el hallazgo de diferencias significativas en la percepción de dificultad de los maestros en tareas de combinación (Dificultad Percibida Combinación 1 F ( 4,35 ) =3,450, p = .018), puesto que estas son las tareas “más fáciles” y que suelen usarse en el aula para enseñar a sumar y restar (p. ej. Pablo tiene 4 objetos y Pedro tiene 5 objetos ¿cuántos objetos tienen entre los dos?). En este caso la tendencia es que los profesores de los grados superiores evalúan la tarea como más fácil que los de los grados inferiores.
El análisis de correspondencias múltiples global reveló una estructura con alta consistencia interna en las dos dimensiones halladas (Dimensión 1, α = .932 Autovalor = 10.95, % varianza = 27.39; Dimensión 2, α = .928 Autovalor = 10.47, porcentaje de varianza = 26.18; se alcanzó el valor de prueba de convergencia en la iteración 40).
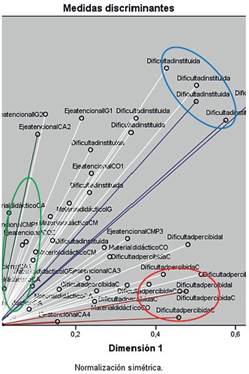
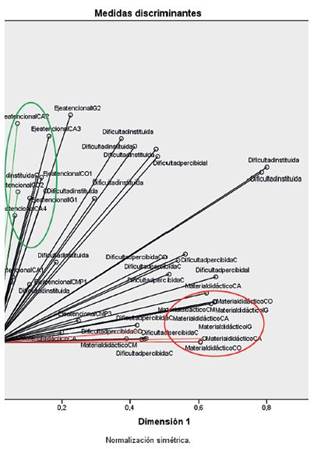
La primera dimensión agrupa fundamentalmente la exigencia en los ítems difíciles mientras la segunda asocia la exigencia de algunos de los ítems fáciles con la de dos de los más difíciles (igualación 1 y 2) y con el punto al cual el docente quiere que el estudiante atienda (Eje atencional en igualación 1 y 2). Las cuantificaciones de las variables en la dimensión 2 muestran que los niveles relevantes para esas categorías tienen que ver con que se exigirá poco esfuerzo (2.833 en ambos ítems) de parte del estudiante si es que este no dirige su atención a números y otras entidades abstractas (- 4.408 eje atencional Igualación 1) o representaciones de objetos concretos vinculadas a la tarea (- 2.085). La tabla 1 muestra las medidas discriminantes de las variables analizadas, se resaltan con color rojo las variables con mayor saturación en la dimensión 1, con color verde las variables con mayor carga en la dimensión 2.
La asociación entre las variables genera una estructura en la que pueden evidenciarse claramente tres grupos diferenciados que corresponden a: 1) Material didáctico (Dimensión 2), 2) Dificultad instituida y 3) Dificultad percibida (Dimensión 1) (Figura 1).
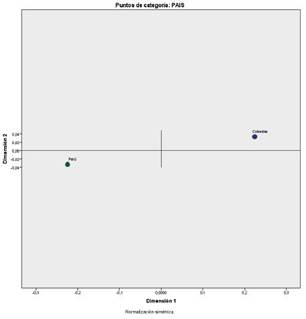
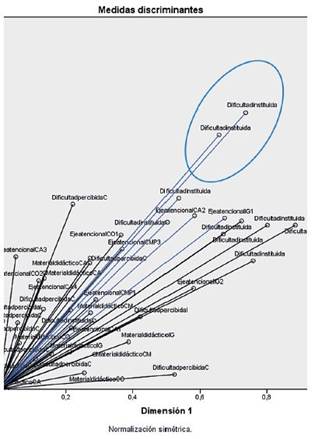
La proyección de la variable ilustrativa “País” en los ejes muestra que la dimensión 1 de dificultad percibida es una dimensión que está un poco más distanciada de la actividad mediacional de los docentes de ambos países. Perú se ubica directamente en la dimensión 2 que corresponde al material didáctico, mientras que Colombia se ubica en una agrupación de dificultad instituida. Esto puede observarse en la Figura 2.
Lo anterior sugeriría que la sensibilidad del docente a la manera como el estudiante percibe las situaciones de adición y sustracción (dificultad percibida) es independiente de la actividad mediacional de adaptación al contexto educativo específico que realizan los docentes de uno u otro país. Ahora bien, el gráfico ilustra el tipo de preocupaciones que ocupa a los docentes en cada sociedad: mientras que en Perú los docentes se enfocan en la organización de actividades y experiencias que fomenten el aprendizaje, en Colombia, el énfasis de la labor de los maestros se halla en la institución de tareas con diversos niveles de complejidad.
Para aclarar las especificidades de la planeación docente en cada contexto se procedió a la realización de los análisis de correspondencias múltiples (ACM) segmentado por país. El ACM con los datos del Perú arrojó una estructura con una consistencia interna alta (dimensión 1, α = .959 Autovalor = 15.28, porcentaje de varianza = 38.21; dimensión 2, α = .932 Autovalor = 10.97, porcentaje de varianza = 27.42; se alcanzó el valor de prueba de convergencia en la iteración 66).
La primera dimensión en los docentes peruanos está definida por el esfuerzo exigido por los maestros para tareas difíciles (igualación 1 y comparación 1) y las cuantificaciones revelan que se trata del esfuerzo activo del docente por calibrar la situación de modo que no implique ni un esfuerzo excesivo (igualación 1 = -3.572, comparación 1 = -3.572) ni uno insuficiente (igualación 1 = -3.864, comparación 1 = -3.864). La asociación con ítems referidos a la preferencia de material didáctico externo al aula (material didáctico comparación 1 = -3.774) y a la idea de que esos ítems son percibidos como difíciles por el estudiante (dificultad percibida comparación 1; fácil = -2.514, difícil = 1.174) revela que la reflexión pedagógica en el caso de los maestros peruanos está orientada a facilitar la experiencia de aprendizaje de los niños adecuando el entorno material para propiciar la superación de dificultades. La Figura 3 muestra el comportamiento de las variables según las medidas discriminantes del modelo para Perú, junto con las mayores saturaciones en cada dimensión.
La segunda dimensión profundiza esta tendencia mostrando que el objetivo principal de la mediación matemática en Perú es lograr que el niño dirija su atención hacia números, segmentos de recta y otras entidades abstractas (cuantificaciones acordes en Eje atencional igualación 2 = 2.273 y Eje atencional en cambio 2 = 3.671).
Finalmente, el análisis de correspondencias para el caso colombiano arroja una estructura altamente consistente (dimensión 1, α = .952 Autovalor = 13.96, porcentaje de varianza = 34.90; dimensión 2, α = .945 Autovalor = 12.73, porcentaje de varianza = 31.84; se alcanzó el valor de prueba de convergencia en la iteración 39), que es diferente del ACM peruano.
Aunque en la primera dimensión también destacan los ítems relacionados con el esfuerzo exigido al aprendiz en tareas difíciles (cuantificaciones en Dificultad instituida de igualación 1 y 2; poco esfuerzo =-2.230, mucho esfuerzo = 2.889) la intención del docente no es la de regular el nivel demandado, sino más bien la de fomentar la competencia del aprendiz enfrentándolo a situaciones más complejas y exhortándolo a atender a números y otros conceptos abstractos (Cuantificación en eje atencional igualación 1 = 3.395, igualación 2 = 0.773) y representaciones de objetos propicias para la suma y la resta (Cuantificación en eje atencional igualación 1 = 1.610, igualación 2 = 1.448).
La segunda dimensión revela una tendencia paralela, para el caso de ítems fáciles que son los problemas de cambio y comparación. Cabe destacar que en este caso la actividad mediacional del maestro consiste en direccionar la atención del aprendiz lejos de su cuerpo (cuantificaciones en eje atencional cambio 2 = - 3.138, eje atencional comparación 3 = -2.061) y centrarla en representaciones de objetos y números abstractos (cuantificaciones en eje atencional cambio 2; representaciones = 1.599, eje atencional comparación 3; números = 1.607).
La Figura 4 muestra el comportamiento de la tendencia y las medidas discriminantes del modelo en el caso colombiano.
Discusión y conclusiones
Los resultados son consistentes con la idea preliminar de que la planeación docente es un tipo de actividad mediacional caracterizada por el esfuerzo reflexivo del maestro dirigido a adaptar el conocimiento disciplinar a las condiciones percibidas en su contexto educativo específico. Los datos muestran que el pensamiento de los profesores se enfoca en encontrar alternativas que le permiten acondicionar diversos elementos de las situaciones de aprendizaje para promover fines específicos que son sensibles en su comunidad.
Los resultados obtenidos indican que no hay diferencias significativas en las variables cuantitativas analizadas para las dos sociedades incluidas en el estudio (Perú y Colombia). Esta convergencia de las apreciaciones, junto a la alta consistencia de las mediciones apunta a que la actividad reflexiva de los docentes sigue parámetros (criterios normativos) concordantes, en ambos países la actividad mediadora se apoya en estándares curriculares similares, lo cual determina que los docentes desarrollen: a) Una sensibilidad similar a la experiencia de dificultad de sus educandos, y b) Unos niveles de exigencia concordantes en los que los ejercicios y tareas propuestos a los educandos exigen normalmente los mismos niveles de esfuerzo.
Ahora bien, el panorama parece ser muy diferente cuando se piensa en la variación de la reflexión docente conforme al grado escolar en el que se enseña. En esta faceta, las diferencias en las estimaciones son consistentes con lo que debería esperarse debido a la evolución de la interacción maestro-estudiante en el contexto educativo formal. El asunto central aquí es que los profesores perciben (quizás irreflexivamente) el avance en el aprendizaje de los estudiantes y por ello dejan de apreciar las tareas más fáciles como una fuente potencial de problemas para sus pupilos. Asimismo, en los grados superiores, el docente refina su nivel de exigencia y suelen diseñar situaciones que exigen un nivel de esfuerzo superior, lo cual seguramente está relacionado con el propósito de preparar a los aprendices para los desafíos que implican el aprendizaje de conceptos más complejos como los de la multiplicación y la división.
El uso del análisis de correspondencias múltiples (ACM) para organizar la información y sugerir las tendencias cualitativas cruciales se mostró como una estrategia muy sólida y bastante eficaz en la medida en que clarifica de manera suficiente el sentido de las consideraciones de los docentes al pensar en su actividad ajustada a su propio contexto educativo. Las asociaciones establecidas entre las variables categóricas (material didáctico y eje atencional) y las variables continuas discretizadas (dificultad percibida y dificultad instituida) revelan un panorama que amplía la comprensión de los asuntos deliberados por los docentes al pensar en el acercamiento del conocimiento matemático a los niños con dificultad.
La diversidad en la estructura de los datos es consistente con la adopción por parte de los docentes de cada país de un perfil planificador con orientación diferente. En Perú, el interés de los profesores por el material didáctico está estrechamente relacionado con su compromiso activo como mediadores por actuar como agentes que facilitan la experiencia de aprendizaje. El énfasis de los maestros en Colombia se centra más bien en dirigir la atención de los niños a conceptos numéricos y formas abstractas, lo que demuestra su preocupación por lograr una adecuada inserción del infante en la tradición intelectual y académica que exige la vida escolar.
Nótese que lo que el análisis revela es una variación en el foco de atención al que los docentes de los dos países orientan su reflexión al planear sus actividades como mediadores del aprendizaje. De tal modo, mientras los docentes en el Perú se preocupan primordialmente por facilitar la experiencia de aprendizaje del educando, entre los maestros colombianos la principal inquietud tiene que ver con garantizar que los estudiantes alcancen los niveles de competencia óptimos para el resto de su vida escolar.
Teniendo en cuenta lo anterior, estas tendencias constituyen un punto de partida interesante para la discusión de políticas e iniciativas dirigidas al mejoramiento de los procesos de enseñanza-aprendizaje en la matemática inicial. Dada la importancia social del fortalecimiento de estos procesos en ambas naciones valdría la pena profundizar los alcances de este estudio mediante otros esfuerzos de investigación que: a) Se enfoquen aún más en las condiciones específicas del proceso de enseñanza-aprendizaje y b) Aborden otras facetas de la interacción educativa en el aula que son pertinentes para entender las dinámicas de cada nicho sociocultural.
En ese sentido, el diseño de experiencias centradas en los objetos de aprendizaje, la creación de oportunidades para enriquecer la experiencia del aprendiz, y la sensibilidad a sus necesidades constituyen una aproximación promisoria para comprender las dificultades en el aprendizaje matemático. Hay que abordar además un desafío adicional, profundizar los análisis sobre la estructura semántica de los problemas de adición y sustracción desde esta perspectiva teórica situada, ya que posiblemente los aspectos lingüísticos de los problemas aritméticos, así como la configuración de las prácticas de aprendizaje matemático inciden en la actividad mediadora del docente.