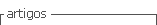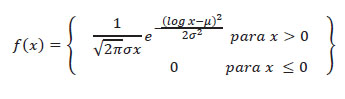COMENTARIOS

Normal y lognormal: dos distribuciones de frecuencias y una Teoría Neutral Unificada para estudiar los bosques tropicales

Normal, and lognormal: two frequency distributions, and one Unified Neutral Theory for studying Tropical forests

 

Edgardo I. Garrido-Pérez* ¹, Laura González ^1,2, Jairo Cabrera ³, Jamil Rojas-Salvatierra ¹, María I. Arias-Pizarro ¹, Mathew Tello ^1,3

1 Asociació Llapis i llavors (Pencil and Seeds), Calle Aragó 565 Bajos, Barcelona, España.

2 Electronic and Biomedical Engineering Department, University of Barcelona, Martí i Franqès, 1, Barcelona, Spain.

3 Universidad Regional Amazónica –Ikiam, vía Muyuna km.7, Tena 150150, Napo, Ecuador.

---

Resumen

Los inventarios de biodiversidad en sitios contrastantes obtienen datos con distribuciones normales y lognormales, útiles para cuantificar cómo el cambio climático afecta a los bosques del mundo. Sin embargo, casi todos los biólogos están familiarizados con la normal, pero menos discuten el por qué la distribución lognormal de frecuencias relativas de especies ocurre en tantas comunidades bióticas. Pretendemos incorporar a más estudiosos a dicha discusión. Tanto la normal como la lognormal tienen medias y valores extremos. Ello es consistente con el teorema del límite central; válido cuando los datos de un muestreo provienen de procesos aleatorios y el muestreo ha sido estocástico y representativo. Según la Teoría Neutral Unificada de la Biodiversidad y la Biogeografía de Steve Hubbell, basta considerar que la natalidad, mortalidad, migraciones y especiación en una comunidad, y desde la metacomunidad circundante, ocurren al azar y simétricamente entre especies, para explicar que las frecuencias relativas de la comunidad sigan una distribución lognormal. Ello es consistente con la Biogeografía de Islas, y se puede aplicar –por tanto a la articulación de abundancias relativas de especies arbóreas en bosques que se regeneran por sucesión secundaria, donde el sitio talado constituye una isla que luego es colonizada. En el sofisticado siglo XXI, conocimientos numéricos tan simples, como la normal y la lognormal, siguen siendo necesarios para mover las fronteras de la ciencia afrontando temas permanentes: por qué en tantos lugares hay especies más abundantes que otras, y cómo se puede contrarrestar la pérdida de las especies en dificultad.

Palabras clave: Abundancias relativas; Inventarios de biodiversidad; Muestreo aleatorio; Navaja de Ockham; Teorema del límite central.

---

 Abstract

Biodiversity surveys among contrasting sites get normal, and lognormal distributed data used for quantifying how Climate Change affects forests around the world. Yet most biologists are familiarized with the normal distribution, while few discuss why the lognormal distribution of relative frequencies of species is so common in many communities of living beings. We aim to add more researchers into such a discussion. Both normal and lognormal have mean and extreme values –which is consistent with the Central Limit Theorem. Such a theorem is valid when the data come from random processes, and when the sampling excercise of collecting the data has been stocastic and representative. According to Steve Hubbell’s Unified Neutral Theory of Biodiversity and Biogeography, random birth, death, migration and speciation in a community –and from the surrounding metacomunity are enough for generating lognormal distributions of relative frequencies of co-existing species. That is consistent with Island Biogography, and is applicable to the assembly of relative abundances of tree species during secondary succession, where the clear-cut site is an island further colonized by tree species. Deep into the sophisticated 21st century, simple numerical knowledge like the normal and lognormal are still needed for moving the borders of science by facing permanent subjects: why in so many places some species are more abundant than others, and how to tackle the loss of endangered species.

Keywords: Biodiversity surveys; Central limit theorem; Random sampling; Relative abundances.

---

1. Introducción.

Entre los recursos matemáticos más útiles para estudiar la biodiversidad están las distribuciones de frecuencias. Un ejemplo ya clásico de su aplicación es en los inventarios florísticos, donde las distribuciones de frecuencias han permitido detectar diferencias en las diversidades y composiciones de especies de árboles tropicales en distintos sitios (v.g. Pyke et al. 2001), coadyuvando a responder preguntas como qué tanto afectan el cambio climático y las variaciones del suelo a la diversidad de árboles tropicales (v.g. Esquivel-Muelbert et al. 2017, Clinebell et al. 1995). En estos estudios se hacen parcelas de tamaños homogéneos ( v.g Phillips & Baker 2003) en lugares con climas y suelos diferentes (v.g. Esquivel-Muelbert et al. 2017), se realiza un inventario de la flora en dichas parcelas, y se buscan patrones de cambio entre parcelas mediante gráficas y estadísticas paramétricas y multivariadas. De esta manera es como se descubrió que los aumentos en la intensidad de las sequías reducen la diversidad en los bosques tropicales (Esquivel-Muelbert et al. 2017, Clinebell et al. 1995). Otros estudios, también clásicos (v.g. Pascarella et al. 2000, Rivera et al. 2000), han permitido identificar hasta qué grado los usos del suelo como la ganadería, la producción agroforestal y la agricultura itinerante afectan a la diversidad de especies de plantas que adquiere una selva cuando se regenera mediante la sucesión secundaria (Garrido-Pérez et al. 2017). Eso a su vez es muy importante para los países que necesitan conservar y ajustar sus ritmos de clareo de los bosques a las velocidades de recuperación forestal sin perjudicar la producción alimentaria (Garrido-Pérez & Sidali 2016). La conexión de todo lo antedicho con las distribuciones de frecuencia estriba en que esos estudios analizan sus datos mediante estadísticas paramétricas (v.g regresiones, ANOVA), las cuales se basan en una distribución normal de las frecuencias de los datos de campo (Blair & Taylor 2008). Así que, para quienes se inician en el estudio de la biodiversidad y su conservación, es conveniente dedicar algo de tiempo al entendimiento de la distribución normal; de lo contrario no se podrán comprender muchos estudios clave para la ecología, ni sus métodos.

El reto de las abundancias relativas de las especies

Más aún, también es necesario comprender la cantidad de veces con que aparecen unas especies con respecto a otras; esto es, las distribuciones de frecuencias de esas apariciones, antes de explorar la complejidad de procesos combinados que hacen que, en un sitio cualquiera, unas especies sean más abundantes que otras (Hubbell 2008, De Marco Júnior 2006). Cuando se hace un listado de especies en una parcela de bosque tropical se cuentan los individuos de cada especie, y se ordenan esos valores de la especie más abundante a la menos abundante. De ahí suelen obtenerse gráficos como el de la Figura 1a. Se trata de un patrón muy común en los inventarios de biodiversidad en los trópicos, con una especie muy abundante, otras con abundancia moderada, y otras con tan solo uno o dos individuos por hectárea. Luego de explorar distintas maneras de transformar los datos, Preston (1948) encontró que, al modificarlos mediante el logaritmo de base 2, los datos adquieren una distribución que, por su semejanza a la normal, se conoce como lognormal (Fig. 1b). La lognormal es tan común que siempre ha desafiado a los investigadores que tratan de determinar sus causas biológicas. Por ejemplo, si las especies raras lo son por alta mortalidad debido a alguna plaga, entonces los conservacionistas podrían controlarla en favor de aquellas especies. Así que, una vez más, a los ecólogos y conservacionistas les conviene estudiar las distribuciones de frecuencias para entender mejor los bosques.

Por mucho tiempo ha predominado la idea de que la especie más abundante en un terreno (barra más alta de la Fig. 1a) llega a serlo porque sobrevive mejor que sus vecinas a una miríada de contingencias. En concreto, esta "escuela de pensamiento" de la ecología de comunidades considera que las especies más abundantes son mejores que las otras para desempeñarse en procesos como: competir por recursos como la luz, el agua y cada uno de los nutrientes del suelo cuando estos escasean, tener un metabolismo más eficaz, evitar o cicatrizar después del ataque de animales herbívoros, microorganismos patógenos o incluso vientos fuertes, dotar a las semillas de más y mejores recursos favoreciendo así a la prole, o producir muchas semillas –aumentando con ello la probabilidad de colonizar sitios favorables. Todo eso está tan documentado y explicado que aparece en los libros de texto (v.g. Begon et al. 2009) y artículos de revisión ampliamente consultados (v.g. Martínez-Ramos 1994). Sin embargo, desde hace algunas décadas Stephen P. Hubbell (Hubbell 1997) está desafiando al pensamiento clásico de la ecología de comunidades argumentando que, en vez de tantas variables, solamente la natalidad, la mortalidad, la migración (y la especiación) al azar y parejas entre especies bastan para explicar las distribuciones de frecuencias relativas de estas en los trópicos. A eso Hubbell lo denominó Teoría Neutral Unificada de la Biodiversidad y la Biogeografía (Hubbell 2001, Rosindell et al. 2011). Ello causó mucha discusión: más de 200 artículos sobre el mismo tema en menos de 10 años (Cassemiro et al. 2008) y aún en aumento. Como buena parte de la teoría antedicha se basa en las distribuciones de frecuencias, es necesario entender éstas para poder formar parte de uno de los temas más apasionantes y permanentes de la ecología: por qué tantos inventarios de biodiversidad en lugares distintos producen gráficas como las de la Figura 1.

Los objetivos de este escrito son:

–

Familiarizar a los lectores con dos distribuciones clave para entender tanto la ecología como las estadísticas asociadas a ella: la distribución normal o gaussiana, y la distribución lognormal de abundancias relativas de especies de seres vivos.

–

Ayudar a los lectores a comprender la Teoría Neutral Unificada de la Biodiversidad y la Biogeografía (de aquí en adelante UNTB, por sus siglas en inglés) en lo concerniente a las distribuciones de abundancias relativas, y su importancia para simplificar y ordenar la interpretación de los resultados de los inventarios de biodiversidad.

2. Los muestreos representativos aleatorios y la distribución normal.

La distribución normal suele aparecer cuando, luego de que un muestreo es representativo, se adquieren los valores de alguna variable continua (Blair & Taylor 2008). Ejemplifiquemos primero qué es un muestreo representativo aleatorio. Digamos que tenemos una olla sopera llena de canicas de colores, las mezclamos bien, y luego sacamos un puñado de esas bolitas. Si hacemos eso, es esperable que los colores de las canicas obtenidas representen las proporciones de esos mismos colores dentro de la olla. Si en la olla hay muchas bolitas rojas y pocas blancas, el puñado de canicas debería tener muchas bolitas rojas y pocas blancas. Por el contrario, si el puñado de bolitas tiene pocas rojas y muchas blancas, entonces pasó algo que hizo que la muestra violara la norma de lo que había. En el ejemplo antedicho, la variable "color de las canicas" no es continua, sino que se la puede considerar categórica, con dos categorías: rojo y blanco. Visto detalladamente, el color también puede considerarse una variable ordinal. Por ejemplo, ordenando de "menos rojo a más rojo" tendríamos: blanco, rosado muy tenue, rosado tenue, rosado claro, rosado oscuro, rojo claro, muy rojo, y rojo-negruzco. Más aún, si exponemos esos colores a una luz con características conocidas, y si usamos aparatos especiales para medir la longitud de onda de la luz que reflejan esos colores, entonces podemos expresar el color en valores de longitud de onda (v.g. en nanómetros). Aunque no siempre se puede, se recomienda convertir cualquier variable en variable contínua, incluso mediante la creatividad personal o el uso de aparatos. Porque eso aumenta la objetividad y permite críticas más precisas de parte de otros científicos.

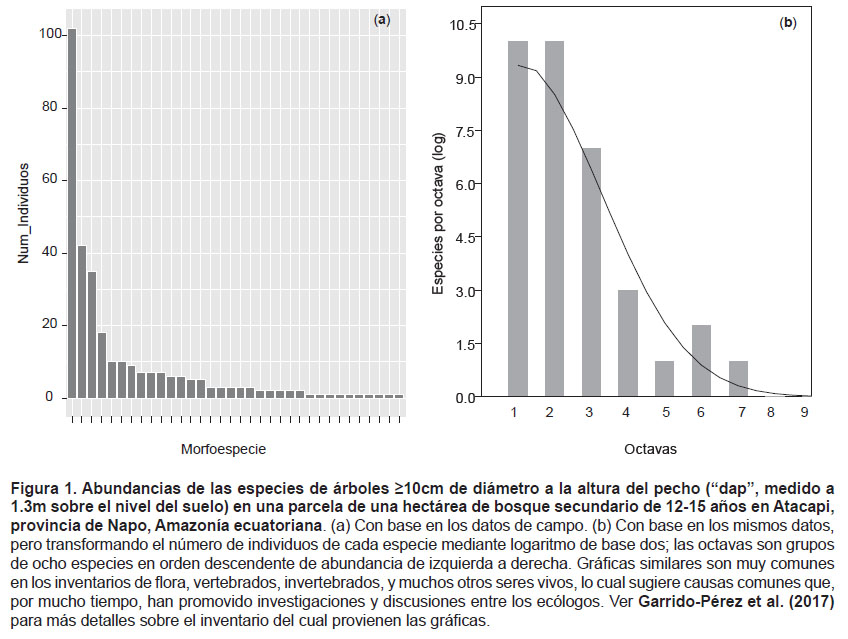
Usemos ahora otro ejemplo, también de muestreo representativo aleatorio, para explicar la distribución normal y las variables continuas. Digamos que nos vamos a las calles de una ciudad, buscamos al azar a diez mil mujeres que tengan edad entre los 30 y 40 años (es decir, que ya no están creciendo), y medimos la talla de cada una. Esa variable, la talla, es continua: puede adquirir valores decimales –y no únicamente enteros. Ahora digamos que la dama más pequeña midió 1.40 m, y que la más alta medía 2.05 m. Supongamos también que clasificamos a esas diez mil mujeres en clases de tallas de la siguiente manera: clase 1: de 1.40 a 1.45 m; clase 2: de 1.45 m a 1.50 m; clase 3: de 1.50 m-1.55 m, y así sucesivamente. Finalmente, digamos que contamos el número de mujeres de cada clase. Por ejemplo, si tenemos 759 mujeres con tallas entre los 1.40 y los 1.45 m, entonces tenemos 759 mujeres en la clase 1; si 2578 tienen tallas entre los 1.45 y 1.50 m, entonces tenemos 2578 mujeres en la clase 2, y así sucesivamente. Después de hacer todo eso, graficamos los datos (Fig. 2a), con las clases de abundancias en el eje de X, y el número de mujeres que hay para cada clase en el eje de Y. Pues bien, si lo que le pasaba a cada mujer era independiente de lo que le sucedía a la otra (dieta, estrés laboral, etcétera), entonces la gráfica debe adquirir la forma de la llamada distribución normal (Fig. 2a). Ahora bien, imaginemos que tomamos al azar un número de mujeres de esas 10000; supongamos que son 56 y les medimos las tallas. Entonces, si el muestreo fue representativo y hecho al azar, la distribución de frecuencias de las tallas de esa muestra de mujeres debe parecerse a la de la Figura 2b, la cual también es una distribución normal como la de la Figura 2a, aunque con un cambio en la escala del eje de Y debido a que el número de mujeres es menor.

3. La distribución normal y el teorema del límite central.

Continuemos nuestra explicación basada en las estadísticas fundamentales (Blair & Taylor 2008). Examinando visualmente cualquier gráfica de la Figura 2a se nota que las barras más altas; es decir, las categorías con mayor número de mujeres, corresponde a las damas con talla intermedia. O sea, entre los 1.60 m y los 1.80 m; con un pico en torno a los 1.70 m. Dicho en otros términos, hay una tendencia central en las tallas de las mujeres: las muy grandes o muy chicas son pocas; la tendencia es hacia un valor medio llamado media (o promedio) de 1.70 m de estatura. Hay un límite inferior de 1.40 m de estatura, un límite superior de 2.05 m de talla, y un límite central hacia el cual tienden a agruparse los resultados. Ese límite central es la media. La media suele calcularse sumando las tallas de todas las mujeres, y dividiendo eso entre el número de mujeres. Expresando lo antedicho, la función de distribución normal tiene como expresión matemática:

Donde µ es la media y σ² es la varianza. Entonces, µ= (∑x_i/n) donde x_i es la talla de la i-ésima mujer, Σ indica que hay que sumar esas tallas, y n es el número total de mujeres estudiadas; o sea, el tamaño de la muestra (si la muestra equivale a toda la población de mujeres, entonces se usa la N).

Pero, así como hay una tendencia central de los datos, hay valores que se alejan del centro; es decir, que muestran una dispersión con respecto a la media. En nuestro ejemplo, eso se refiere a las relativamente pocas mujeres cuya talla tiende a ser muy grande o muy pequeña; es decir, a acercarse a los límites inferior y superior. Esa desviación con respecto a la media también puede expresarse mediante fórmulas matemáticas. Facilitemos eso con un poco de geometría analítica (Fig. 2a): trazando una línea punteada desde el pico de la curva normal, el cual equivale a la media. De este modo obtenemos –sobre el eje horizontal, precisamente el valor de la media (µ). Puesto que esta operación parte la curva normal en dos mitades simétricas, se dice precisamente que la simetría con respecto a la media es una característica de la curva normal. Si así es, entonces la distancia entre µ y el extremo inferior debe ser similar a la distancia entre µ y el extremo superior. De hecho, en una curva normal, las distancias a partir de la media, hacia cualesquiera puntos a la izquierda tienden a un valor simétrico en algún punto por la derecha, aunque con signo negativo hacia la izquierda y positivo hacia la derecha. Por ello, la mejor forma de cuantificar la dispersión en una curva normal no es sumar esas distancias, pues el resultado sería cero; sino elevar al cuadrado las distancias (anulando así los signos negativos), y luego realizar la suma de cuadrados.

Es decir que, matemáticamente hablando, la suma de cuadrados (sc) se calcula así:

sc= ∑(x -µ)²

Por tratarse del resultado de una adición, la suma de cuadrados es un valor relativamente grande. Si dividimos la suma de cuadrados entre el tamaño de la muestra menos uno (n-1; lo cual se conoce como grados de libertad ¹; Student 1908) obtenemos un valor más pequeño que la suma de cuadrados: la llamada varianza (σ²). La varianza se calcula así:

σ² =sc/(n-1)

o sea

σ² = ∑(x -µ)²/(n-1)

Al igual que la suma de cuadrados, la varianza es una medida de dispersión: indica qué tanto los valores de la muestra (en este caso, de las tallas de las mujeres) se alejan de la media. Existen otras medidas de dispersión asociadas a la varianza, y por ende a la suma de cuadrados; apenas una de ellas es la desviación estándar, (σ) que es la raíz cuadrada de la varianza. El apasionante análisis de las muchas características de la distribución normal escapa a los objetivos de este escrito y se puede abordar consultando cualquier libro de estadísticas (v.g. Blair & Taylor 2008). Sin embargo, lo expuesto hasta aquí brinda bases para quien desee profundizar en las estadísticas paramétricas. También nos permite presentar el teorema del límite central y, luego de eso, los fundamentos de la distribución lognormal y la UNTB.

El teorema del límite central posee dos premisas. Primera: considérese que se hacen mediciones de variables continuas a entidades obtenidas por muestreos aleatorios, de modo que esas entidades son independientes unas de otras, (como las mujeres de nuestro ejemplo). Segunda: esos datos tienen varianza finita (con límites inferior y superior establecidos, como en el caso de las damas de nuestro ejemplo). Si ello es así, entonces el conjunto de los valores obtenidos seguirá una distribución normal; con un límite central cercano a la media muestral. En otras palabras, si usted encuentra en el mundo datos cuya distribución es normal, entonces usted tiene fuertes motivos para pensar que esos datos fueron generados por un muestreo aleatorio, y que las cosas que se muestrearon eran independientes unas de otras. Por eso Hubbell (2001) propuso que en los inventarios de biodiversidad en los que las distribuciones de abundancias relativas de especies sean lognormales hay motivos para pensar que los procesos ecológicos que determinaron eso han sido aleatorios sin afectar necesariamente a unas especies más que a otras (Volkov et al. 2003), tal como explicaremos de inmediato.

4. Los procesos aleatorios: hacia la Teoría Neutral Unificada de la Biodiversidad y la Biogeografía (UNTB).

De acuerdo con la UNTB, una comunidad de árboles se articula mediante procesos al azar y simétricos de nacimiento y muerte en un lote de terreno, así como de inmigración desde el bosque circundante a ese terreno (Hubbell 2001, Rosindell et al. 2011). "Al azar" significa que no hay especies más "fuertes" o "débiles" que otras: si un árbol muere, es porque tuvo la "mala suerte" de morirse él y no él que estaba al lado (Hubbell & Foster 1986): porque lo partió un rayo, porque le cayó un hongo por haber tenido la "desdicha" de haber germinado en el sitio donde después el hongo llegaría, etcétera. Y si ese árbol difunto es reemplazado por otro, existen dos posibilidades (para la UNTB). La primera es que lo reemplace otro árbol nacido en el mismo terreno; es decir, que el reemplazo sea por natalidad. Según la teoría, ese árbol que lo reemplaza llega allí "por pura casualidad": una semilla produjo una plántula que luego se hizo juvenil con la suerte de estar en el lugar apropiado en el momento oportuno para reemplazar al árbol difunto (Hubbell & Foster 1986, Hubbell 2001). Digamos que eso ha sido posible porque, por casualidad, la semilla cayó traída por el viento, o por un pájaro que se la había comido y luego se le antojó regurgitar o defecar la semilla en ese lugar, donde hay un espacio abierto, en vez de hacerlo en otro lugar. Existen trabajos clásicos que apuntan a que la elección de qué semillas comer, así como el vuelo y la percha de los pájaros sobre los árboles no ocurren al azar, por lo que la dispersión de semillas tampoco lo es (Martínez-Ramos 1994). Sin embargo, Hubbel y Foster (1986) indican que el que un pájaro elija a una cierta semilla y no a otra, o que un rayo parta a un árbol y no a su vecino, y que la semilla que germine para reemplazarlo corresponda a la que trajo un pájaro y no otro, son ejemplos de procesos meramente aleatorios. Así que, de acuerdo con la UNTB, la semilla que proveniente de un árbol en un lote, arriva, germina, crece y reemplaza a un árbol difunto en un punto dado de ese lote, lo hace por casualidad. Todo esto ilustra lo que la UNTB llama "natalidad aleatoria" a lo interno de un lote o comunidad forestal. La segunda posibilidad, sobre todo si hay un bosque grande alrededor del lote, es que la semilla que reemplaza al árbol difunto venga desde afuera del terreno; es decir por inmigración. Y ésta, según la UNTB, puede ser también al azar de un modo parecido al antedicho (el viento, el pájaro, etcétera), ilustrando lo que la UNTB considera "inmigración aleatoria". De manera que, como bien aclara Hubbell (2001), la UNTB se acerca más a las teorías que explican la articulación de las comunidades forestales con base en la dispersión de las semillas, que con base en el reparto de nichos ecológicos clásicamente aceptado en los libros de texto de ecología (v.g Begon et al. 2009).

 

5. La distribución lognormal y la UNTB como teoría de muestreos.

En muchos inventarios de flora se obtienen resultados parecidos a los de la Figura 1a. Sin embargo, hacia el año 1948, un ingeniero amante de la biología llamado Frank W. Preston tomó los datos de varios gráficos parecidos y los transformó más o menos de la manera siguiente (Preston 1948). Tomó el eje de Y y lo puso en la horizontal (o sea, lo puso en lugar del eje de X). También, al eje de y, en vez de dejarlo con los datos de campo (como en la Fig. 1a), lo transformó usando el logaritmo de base 2 (mejor conocido como "log"), y en el eje vertical puso el número de especies. Aparentemente, Preston tenía buenos conocimientos de música, particularmente de piano: las teclas de un piano están ordenadas de izquierda a derecha en grupos de ocho llamados "octavas"; las octavas a la izquierda producen sonidos graves, las de la izquierda generan sonidos casi imperceptibles. Con esa metáfora de las octavas, Preston graficó sus datos: colocó las especies de mayor abundancia hacia la izquierda y las menos abundantes a la derecha, como en la Figura 1b. Preston notó que, con ese arreglo, la curva seguía una forma de campana semejante a la de una distribución normal. Pero, como los datos habían sido "log-transformados", se la conoce como distribución lognormal (Fig. 1b) con la siguiente expresión:

FORMULA N 2

Hubbell hizo lo propio con los datos de las parcelas de la red de investigaciones que fundó, llamada ForestGeo, particularmente de globos de terreno de 25 – 50 hectáreas ubicados en la isla de Barro Colorado (Canal de Panamá), Pasoh (Indonesia) y Yasuní (Ecuador) (Hubbell 2008). Al hacerlo, Hubbell también encontró distribuciones lognormales (Hubbell 2008, Volkov 2003) (Fig. 3a). Lo mismo ha sido confirmado para parcelas de una y 25 hectáreas en Amayacu (Colombia), Manaus (Brasil) y el propio Yasuní, (Duque et al. 2017). Nuestro equipo de trabajo también lo ha reportado para parcelas de una hectárea en bosques secundarios de la Amazonía ecuatoriana (Garrido-Pérez et al. 2017). Así que, aunque la distribución lognormal no ocurre en todas partes, sobre todo para muestras muy grandes, sí es bastante común para distintos organismos y lugares del mundo (Baldridge et al. 2016).

Por motivos financieros o de otro tipo, muchos inventarios florísticos no pueden capturar todas las especies de un bosque porque el área muestreada no es lo suficientemente grande. Entonces la forma de campana del gráfico no se cumple a cabalidad, pero los datos siguen una función matemática cuya representación geométrica se aproxima a una campana. La función de distribución de esos datos sigue correspondiendo a una lognormal, aunque incompleta (Fig. 3b) (ver también Fig. 1b).

Al igual que la distribución normal, la lognormal, en una muestra abundante y por ende, considerablemente representativa adquiere la forma de una campana (Fig. 3a). Por eso mismo se le puede aplicar el teorema del límite central, tal cual lo hizo uno de los ecólogos clásicos (May 1975). Así, hacia la cima de esa campana se representan las especies, cuya abundancia en el inventario es moderada; hacia la cola izquierda aparecen las especies raras o menos abundantes, y hacia la cola derecha aparecen las especies más abundantes; o sea, comunes. Si en lugar de graficar los datos como en la Figura 3 mantenemos el logaritmo de las abundancias en el eje de las Y, dejando en el eje de las X un ordenamiento de las especies que vaya de la más abundante a la menos abundante, nuestra gráfica se parecerá a la de la Figura 2b, lo cual también deja ver una distribución lognormal. De hecho, en dicha Figura 3a se confirma que hay más puntos (o sea, especies) con abundancias intermedias, y menos especies, tanto muy abundantes (extremo izquierdo), como poco abundantes (cola hacia la derecha; Fig. 2b). Así, tanto la Figura 2 como la Figura 3 ilustran que May (1975) tuvo razón: la distribución lognormal es consistente con el teorema del límite central. Si dicho teorema es cierto, entonces los procesos que determinan el patrón lognormal de distribución de las abundancias de las especies deben ser aleatorios. De acuerdo con la UNTB, esos procesos aleatorios que articulan las comunidades arbóreas serían los de natalidad, mortalidad e inmigración del modo explicado en párrafos anteriores. De todo lo antedicho se deduce que la UNTB es una teoría de muestreos (Rosindell et al. 2011): las especies que se encuentran en un momento dado en una parcela de bosque han llegado allí traídas por la dispersión de semillas, a manera de muestra del conjunto de especies de la zona circundante, con reemplazos de los árboles difuntos por inmigración desde dicha zona, o desde adentro del propio terreno mediante natalidad.

6. UNTB, biogeografía de islas y sucesión secundaria

Cabe destacar que la UNTB es una aplicación de otra teoría, ya clásica, conocida como la de Biogeografía de islas (McArthur & Wilson 1963). Han pasado más de 50 años después de su formulación, pero la biogeografía de islas sigue siendo muy útil para entender el ensamble de las comunidades de seres vivos, por lo que aparece en los libros de texto (v.g. Begon et al. 2009). Esencialmente, cualquier globo de terreno es una "isla" progresivamente ocupada por especies desde los alrededores. Durante dicha colonización, las especies se van acumulando, pero la variedad de esas especies para cada lote dependerá de: (a) el tamaño del lote o isla –pues los terrenos más grandes tienen más espacio para acumular especies. (b) La edad de la isla; pues los sitios más viejos han tenido más tiempo para acumular especies. Cabe resaltar que, si lo que se está formando es un bosque secundario, dicho lote es la "isla". También (c): la distancia al continente o fuente de donde provienen las especies –dado que las islas más cercanas pueden acumular más especies (McArthur & Wilson 1963). Como se ve, para los efectos de un globo de terreno dado rodeado de un bosque, el propio lote funciona como "isla" donde se ubica la comunidad forestal, y los alrededores pueden ser considerados como el "continente", es decir, la metacomunidad de donde, a manera de muestreo, llegan al sitio las especies que configuran la comunidad de bosque secundario. Por eso la teoría de biogeografía de islas, al igual que la UNTB, es una teoría basada en el muestreo aleatorio (Hubbell 2001, Rosindell et al. 2011).

En otro estudio (Garrido-Pérez et al. 2017), nuestro equipo aplicó la teoría de biogeografía de islas y la UNTB para proponer cómo unos parches de bosques secundario amazónico debieron haberse ido configurando como comunidades, con distintas especies arbóreas, durante la sucesión secundaria. En concreto, primero los espacios eran bosques que incluían bancos de semillas en el suelo. Luego fueron talados para instalar potreros y agricultura de "chakra" por los indígenas Kichwa, después debieron haber sido re-colonizadas por especies forestales provenientes de la amplia selva circundante, la cual no había sido talada en mucho tiempo; incluso los humanos ayudaron a dispersar las semillas –por ejemplo, al comer frutas y tirar las semillas. Pensamos que eso ocurrió mayormente de conformidad con la biogeografía de islas y la UNTB, por dos motivos: (1) las especies de la zona virtualmente no rebrotan por tocones luego de la tala, sino solo por semillas. Son precisamente las semillas las que arriban y se almacenan en cualquier zona clareada o "isla". Además de eso: (2) las comunidades de especies del bosque secundario del sitio, hoy en día, siguen distribuciones de abundancias relativas de tipo lognormal (v.g. Fig. 1a) (Garrido-Pérez et al. 2017), por lo que la explicación más directa y robusta es que la natalidad, mortalidad e inmigración aleatorias intervinieron en el proceso (ver también Hubbell 2008).

Dado que la sucesión tarda muchas décadas (v.g. Dent et al. 2013), cualquier distribución de abundancias relativas hallada en un inventario de árboles es apenas una "fotografía instantánea" de lo que acontece durante dicho proceso. Si eso es así, y asumiendo que los mecanismos que articulan las abundancias relativas siguen siendo los de natalidad, mortalidad e inmigración aleatorias de las especies arbóreas, entonces el cambio a través de los siglos de las abundancias de unas especies con respecto a otras debe ocurrir también al azar. La UNTB llama a esto "deriva ecológica aleatoria" (Hubbell 2001). Pero en tiempos más largos, tales como las decenas o centenas de siglos que corresponden a muchas generaciones de árboles, las mortalidades extremas pueden causar extinción, mientras que la especiación puede agregar especies, ora surgidas directamente en el lote de terreno, ora por semillas que ingresan de especies originadas en la metacomunidad que circunda el lote (Hubbell 2001). Discutir la matemática subyacente a estos procesos contemplados por la UNTB nos apartaría de los objetivos de este escrito, por lo que invitamos a los lectores a consultar otras fuentes (v.g Rosindell et al. 2011, Hubbell 2001, Chave 2004).

7. Complejidad y riesgos de agnosticismo en la Ecología tropical.

La UNTB, ni es la única explicación posible de la lognormal, ni basta para entender otras características de los bosques tropicales tales como la composición de especies (ver más adelante). Pero sí es lo suficientemente sencilla como para (Hubbell 2008): (a) funcionar como "navaja de Ockham"; esto es, como respuesta más sencilla a la pregunta "por qué en muchos inventarios forestales prevalece la lognormal". Junto a eso (b): servir como eje ordenador de una amplia cantidad de otras explicaciones al cómo se articulan las comunidades forestales (Garrido-Pérez et al. 2017), lo cual exponemos a continuación.

Entre las preguntas que han consumido más tiempo y esfuerzo a través de las generaciones de ecólogos está el por qué hay localidades poco biodiversas, como los bosques templados, donde predomina una sola especie (alejándose de la lognormal), mientras en otros bosques, como los húmedos tropicales no ocurre lo antedicho, sino que la lognormal se mantiene. A diferencia de la UNTB, muchos ecólogos y ecofisiólogos han suministrado prolíficas explicaciones al respecto (ver revisiones en Ruiz 2009, Martínez-Ramos 1994). Procedemos a sintetizar lo que explican dichos autores y la literatura en que se basaron. Como consecuencia de la evolución por selección natural, no todas las especies deberían ser igualmente susceptibles (o adecuadas) ante los diferentes componentes bióticos y abióticos. En concreto: (1) las semillas de distintas especies germinan ante distintos valores de la relación rojo:rojo lejano de las longitudes de onda de la luz que las alcanza. Dicha radiación no les llega siempre, ni en todos lados, exponiéndolas a microorganismos descomponedores antes de germinar. Por su parte, (2) las plántulas, brinzales y juveniles de distintas especies no responden por igual a la intensidad de la luz fotosintéticamente activa que las alcanza. Esto, combinado con (3) los procesos de dispersión de las semillas ( v.g. preferencias de dieta y percha de diversos animales dispersores) genera un arribo y sobrevivencia dispareja entre especies, contribuyendo a anular las posibilidades de que una sola predomine. Aunado a eso, (4) la caída de árboles de distinto tamaño provoca que cada bosque tropical constituya un mosaico de micrositios, con iluminación y temperatura variados, ocupables por especies con cualidades distintas, evitando la monodominancia, aumentando la diversidad (Denslow 1987), y tal vez manteniendo la lognormal. (5)Además existen procesos de reducción del reclutamiento debidos a la mortalidad y a bajas en el vigor del crecimiento causados por herbívoros y microorganismos patógenos, sobre todo los que se contagian desde árboles de la misma especie de las plántulas (Modelo de Janzen y Connell; ver revisión en Ruiz 2009). Es más (6), la presencia de depredadores de los herbívoros, como las arañas, en las inmediaciones de las plántulas, está asociada con un mejor desempeño de estas (Ruiz et al. 2009); lo mismo ocurre cuando los vertebrados carnívoros depredan a los herbívoros (Wright et al. 2000). De modo que también los actores mencionados en los puntos (5) y (6) impiden la monodominancia y mantienen la diversidad de las selvas tropicales.

Junto a todo lo antedicho se acepta la ocurrencia de (7) competencia entre especies por recursos limitados como, por ejemplo, la luz solar –la cual es limitada para algunas plantas cuando las cubren las sombras de otras, el agua– en tiempos de sequía, y las decenas de diferentes nutrientes del suelo útiles para las plantas –algo con lo que los agricultores están muy familiarizados (v.g. Casanova et al. 2007). De hecho, la competencia interespecífica puede ocurrir de manera difusa en los bosques, provocando que las especies favorecidas en unos sitios no sean las mismas en otros sitios (Garrido-Pérez et al. 2012), contribuyendo a evitar la monodominancia. También (8) existen interacciones favorables entre especies (v.g Tirado et al. 2015); por ejemplo, muchas leguminosas asociadas a bacterias fijadoras de nitrógeno enriquecen el suelo con dicho nutriente, lo cual favorece a otras especies e implica que la distribución de las leguminosas –una familia muy numerosa de plantas, puede influir en la articulación de las comunidades forestales. (9) Existen incluso variedades genotípicas y fenotípicas en una misma especie: individuos y tal vez subpoblaciones más capaces que otras de responder a los cambios ambientales, tanto por la dotación genética que heredaron de sus progenitores, como por aclimatización y cambios en su expresión genética inducidos por el ambiente (West-Eberhard 2005). Por ello, los resultados de los procesos que articulan una comunidad no dependen solamente de la amplia variedad de los componentes ambientales, sino también de las diferencias entre especies e incluso a lo interno de una misma especie. Por si todo eso fuera poco (10) una especie de vertebrado (los seres humanos, Homo sapiens) alteran fuertemente los bosques (Gómez-Pompa 1987) y las relaciones entre otros seres vivos y su ambiente, desde los niveles de comunidad local en un lote de terreno (Garrido-Pérez et al. 2017), pasando por amplias selvas como la Amazónica (Levis et al. 2017), hasta la biósfera entera (Garrido-Pérez & Tella-Ruiz 2016).

Pero todos los aspectos arriba indicados, además, actúan de manera simultánea y variable en tiempo y espacio, todo lo cual implica mucha incertidumbre (Garrido-Pérez et al. 2012). Por tal motivo, la ecología de comunidades es considerada una ciencia muy pluralista; incluso ha sido caricaturizada en el habla coloquial diciendo que es la "ciencia del depende" (Bradshaw 2014): depende de la luz, depende de los recursos del suelo, depende de los depredadores, etcétera. Eso equivale a lo que podríamos llamar un "agnosticismo ilustrado": los ecólogos acumularon tanta información y datos sobre problemas complejos, que se convirtieron en vanguardia del estudio de procesos intrincados, y hasta en un paradigma para otras ciencias como las finanzas y el urbanismo que también lidian con el reto de reducir la incertidumbre en el estudio de sistemas complejos (Grimm et al. 2005). No obstante, se ha propuesto que la UNTB puede ayudar a simplificar y articular la complejidad de explicaciones al cómo se ensamblan las comunidades forestales (Hubbell 2008), contribuyendo a revitalizar la ecología.

8. La UNTB como propuesta para el reordenamiento de la Ecología.

De acuerdo con la UNTB, en lugar de confundirse con abundantes e intrincadas explicaciones al por qué de fenómenos como la preeminencia de la lognormal, conviene lo siguiente (Hubbell 2008). (a) Empezar asumiendo que tan solo la natalidad, la mortalidad y la inmigración aleatorias y simétricas entre especies (pese a las diferencias de estas) ensamblan las comunidades forestales (Hubbell 2001), lo cual es consistente con el teorema de límite central. Luego de lo antedicho: (b) añadir gradualmente más explicaciones; o sea, variables explicativas o términos libres –si la explicación es matemática, pero sólo si la influencia de esas variables es respaldada por evidencias contundentes (o si los datos no siguen distribuciones como la lognormal), y si hacen que los modelos se ajusten mejor que la lognormal a los datos obtenidos en el inventario florístico (Hubbell 2008).

Nótese que esto último propone el uso de la UNTB como una "navaja de Ockham". El filósofo Guillermo de Ockham (siglos XIII y XIV DC) aconsejó que, cuando se considere más de una explicación a algún fenómeno complejo, se dé prioridad a la explicación más sencilla (ver más detalles en Riesch 2010). A esto también se le llama "principio de parsimonia", y podría pensarse que el nombre de "navaja" se refiere, metafóricamente, a que su uso "afeita las barbas" de un pensamiento que se ha "enredado" en causas abundantes. Eso no significa que la explicación más simple sea necesariamente la más realista; para testar eso hay que buscar evidencias empíricas. Pero sí permite simplificar y re-ordenar las múltiples explicaciones a un proceso. En ese sentido, la UNTB no descarta que sucedan la competencia, los ataques por patógenos y demás procesos mencionados en el subtítulo anterior. Pero sí propone que sus efectos pueden considerarse neutros; simétricamente difusos entre especies (Rosindell et al. 2011, Hubbell 2008, 2001), de forma tal que la distribución de abundancias de las especies permanece consistente con la lognormal y con el teorema del límite central. Desde esa perspectiva, la herbivoría, la competencia y la infección por patógenos reducen la esperanza de vida y contribuyen a la mortalidad de manera simétrica entre unas especies y otras, lo cual hace que el conjunto del proceso siga siendo neutro y consistente, según Hubbell, con la lognormal (Rosindell et al. 2011, Hubbell 2008). Una mejor captación de nutrientes del suelo puede vigorizar la reproducción, aportando con ello a la natalidad de la población y, a su vez, generando más semillas que, al dispersarse, contribuyen a un flujo migratorio también simétrico entre especies; por ejemplo, a causa de competencia difusa y poca coincidencia espacial entre competidores de las mismas especies antagónicas (Garrido-Pérez et al. 2012, Connell 1990). Esto hace de la UNTB una teoría robusta (Rosindell et al. 2012), capaz de absorber mucha información sin necesidad de alterar el número de variables de la propia teoría, tales como la natalidad, la mortalidad y la inmigración aleatorias. Otro buen motivo para usarla como "navaja de Ockham", reduciendo los "dependes" que por casi un siglo han enmarañado la ecología de comunidades.

Conclusión

Las distribuciones normal y lognormal son tan comunes, que aún en hoy es necesario consultar a los clásicos que las describieron para entender mejor los bosques. Cuando los datos de campo siguen una distribución normal o lognormal, esos datos son consistentes con el teorema del límite central. Este asume que los procesos que generaron las cifras fueron aleatorios, y que los datos provienen de un muestreo representativo. La Teoría Neutral Unificada de la Biodiversidad y la Biogeografía (UNTB) propone que, cuando las frecuencias relativas de las especies de un inventario de biodiversidad local siguen un patrón lognormal, los procesos aleatorios que determinaron eso fueron la natalidad, mortalidad, migraciones, y –en plazos más largos, la especiación. Eso no desdeña el rol de procesos como la competencia, la patogenia, los mutualismos, o un mejor vigor de parte de algunos organismos. Pero la teoría señala que dichos procesos pueden ser lo suficientemente cambiantes en espacio y tiempo, como para que su efecto no opere siempre sobre una misma especie, sino que se difunda de manera pareja entre las especies de una misma comunidad. La sencillez de esa teoría y su concordancia con el teorema de límite central no obligan a aceptarla, pero sí invitan a considerar su uso como eje ordenador de explicaciones más complejas y difíciles de probar.

Quien, a partir de sus cursos de estadística básica, logra entender la distribución normal, ha dado un paso crucial para encarar la UNTB. Eso le ayudará a ordenar ideas y participar activamente en una de las discusiones más relevantes de la Ecología y la Conservación: cómo y por qué en tantos lugares unas especies abundan más que otras, cuáles son las especies en dificultad, y cómo y dónde revertir su pérdida.

Nota:

(1) Básicamente, el grado de libertad se refiere al número de valores posibles de un dato que provenga de una muestra, sin que el mismo dato se repita. Por ejemplo, supongamos que tenemos una muestra de n=10 canicas en un sorteo de lotería, y que cada una está marcada con un número de 1 a 10. Si pedimos a alguien que tome una bolita, la libertad dentro de la cual evitamos que se repita el mismo número será de nueve. Ello equivale al total de canicas en la muestra (n=10), menos la pelotita que es retirada (una), con lo que tenemos que el grado de libertad gl = n-1 = 10‒1 = 9. Nótese que si la muestra es pequeña, el grado de libertad de no-repetición es menor. Por ejemplo, si n=5, entonces gl=4, en lugar de nueve. Sin usar el nombre "grados de libertad", el concepto fue explicado por William Gosset usando el pseudónimo de "Estudiante" (ver en la literatura citada Student 1908).

Agradecimientos

La Asociación Llapis i Llavors (Pencil and seeds), Barcelona, apoyó este trabajo como parte de sus "cuadernos didácticos". Paulina Garrido Pahl aportó la aclaración del arreglo de información en octavas.

Literatura citada

Balridge E., D.J Harris, X. Xiao, & E.P. White. 2016. An extensive comparison of species abundance distribution models. PeerJ4:e2823. doi: 10.7717/peerj.2823.         [ Links ]

Begon M., C.R. Townsend, & J.L. Harper. 2009. Ecology from individuals to ecosystems. 4^th edn. New Jersey: Wiley.         [ Links ]

Blair R.C., & R.A. Taylor. 2008. Bioestadística. Pearson: México.         [ Links ]

Bradshaw C.J.A. 2014. (en línea). Ecological processes depend on. https://conservationbytes.com/2014/05/14/ecologicalprocesses-depend-on/. Acceso 09/11/2017.         [ Links ]

Casanova F., L. Ramírez, & F. Solorio. 2007. Interacciones radiculares en sistemas agroforestales: mecanismos y opciones de manejo. Avances en Investigación Agropecuaria 11(3):41-52. doi:http://www.redalyc.org/pdf/837/83711304.pdf.         [ Links ]

Cassemiro F.A.S., & A.A. Padial. 2008. Teoría neutra da biodiversidade e biogeografia: aspectos teóricos, impactos na literatura e perspectivas. Oecologia Brasiliensis 12(4):706-719.         [ Links ]

Chave J. 2004. Neutral theory and community ecology. Ecology letters7(3):241-253. doi: 10.1111/j.1461-0248.2003.00566.x.         [ Links ]

Clinebell R.R., O.L. Phillips, A.G. Gentry, N. Stark, & H. Zuuring. 1995. Prediction of Neotropical tree and liana speciesrichness from soil and climatic data. Biodiversity and Conservation 4:56-90. doi: 10.1007/BF00115314.         [ Links ]

Connell J.H. 1990. "Apparent" versus "Real" competition in plants. In J.B. Grace, & D. Tillman, eds. Perspectives in PlantCompetition, Academic Press, San Diego. Pp. 9-26.         [ Links ]

De Marco Júnior P. 2006. Um longo caminho até uma teoría unificadapara ecolgía. Oecologia Brasiliensis 10(1):120-126.         [ Links ]

Denslow J.S. 1987. Tropical rainforest gaps and tree species diversity. Annual Review of Ecology and Systematics18(1):431-451. doi: https://doi.org/10.1146/annurev.es.18.110187.002243.         [ Links ]

Dent D.H., S.J. DeWalt, & J.S. Denslow. 2013. Secondary forests of central Panama increase in similarity to old‐growthforest over time in shade tolerance but not species composition. Journal of Vegetation Science 24(3):530-42. doi: 10.1111/j.1654-1103.2012.01482.x.         [ Links ]

Duque A., H.C. Muller-Landau, R. Valencia et al. 2017. Insights into regional patterns of Amazonian forest structure, diversity, and dominance from three large terra-firme forest dynamicsplots. Biodiversity and Conservation 26(3):669-86. doi:10.1007/s10531-016-1265-9.         [ Links ]

Esquivel‐Muelbert A., T.R. Baker, K.G. Dexter KG, et al. 2017.Seasonal drought limits tree species across the Neotropics. Ecography 40(5):618-29. doi: 10.1111/ecog.01904.

Garrido-Pérez E.I, & K.L. Sidali. 2016. Los niveles de organización ecológica: una guía para administrar los recursos naturales y culturales. Investigación y Pensamiento Crítico 4(2):95-114.         [ Links ]

Garrido-Pérez E.I. & D. Tella-Ruiz. 2016. Homo sapiens (Primates: Hominidae): ¿una especie invasora o aún peor? Un retopara potenciar la Ecología y la Biología de la conservación. Puente Biológico 8:43-55.         [ Links ]

Garrido Pérez E.I., R. Durán R, & G. Gerold. 2012. Las relaciones liana-árbol: repercusiones sobre las comunidades arbóreas y sobre la evolución de los árboles. Interciencia 37(3):183-189.

Garrido-Pérez E.I., D. Tella-Ruiz, J. Rojas-Salvatierra, et al. 2017. Human intervention, neutral theory, and the assembly of Amazonian secondary forest communities in Napo, Ecuador. International Journal of Science and Nature 8(3):418-429. doi:http://scienceandnature.org/IJSN_Vol8%283%29S2017/IJSN-VOL8%283%2917-1.pdf.         [ Links ]

Gómez-Pompa A. 1987. On maya silviculture. Mexican Studies/Estudios Mexicanos 3(1):1-7. doi: 10.2307/4617029.         [ Links ]

Hubbell S.P. 1997. A unified theory of biogeography and relativespecies abundance and its application to tropical rain forestsand coral reefs. Coral Reefs 16(5):S9-21. doi: https://doi.org/10.1007/s003380050237.         [ Links ]

Hubbell S.P. 2001. The unified neutral theory of biodiversity andbiogeography. Princeton University Press: New Jersey.         [ Links ]

Hubbell S.P. 2008. Approaching ecological complexity from the perspective of symmetric neutral theory. In W.P. Carson, & S.A.Schnitzer, eds. Tropical Forest Community Ecology, Wiley, Oxford. Pp. 43-159.         [ Links ]

Hubbell, S.P. & R.B. Foster. 1985. Biology, chance and history and the structure of Tropical Rain Forest tree communities. In: Diamond, J.M. & T.J. Case, eds. Community Ecology,Harper and Row, New York. Pp. 314-329.         [ Links ]

Levis C., F.R.C. Costa, F. Bongers, et al. 2017. Persistent effects of Pre Columbian plant domestication on Amazonian forest composition. Science 355(6328):925-931. doi: 10.1126/science.aal0157.         [ Links ]

Martínez Ramos M. 1994. Regeneración natural y diversidad deespecies arbóreas en selvas húmedas. Boletín de la Sociedad Botánica de México 54:179-224.         [ Links ]

May R.M. 1975. Patterns of species abundance and diversity. In:Cody M.L. & J.M. Diamond, eds. Ecology and evolution ofcommunities, Harvard University, Cambridge. Pp.81-120.         [ Links ]

MacArthur, R.H. & E.O. Wilson. 1963. The theory of island biogeography. Princeton, New Jersey.         [ Links ]

Pascarella J.B., T.M. Aide, M.I. Serrano, & J.K. Zimmerman. 2000. Land-use history and forest regeneration in the Cayey Mountains, Puerto Rico. Ecosystems 3:217-228. doi: 10.1007/s100210000021.         [ Links ]

Phillips O.L., & T.R. Baker. 2003. Manual de campo para el establecimiento y remedición de parcelas permanentes. Cantua12:85-93.         [ Links ]

Preston F.W. 1948. The comoness and rarity of species. Ecology29(3):254-283. doi: 10.2307/1930989.         [ Links ]

Pyke C.R., R. Condit, S. Aguilar & S. Lao. 2001. Floristic composition across a climatic gradient in a neotropical lowland forest. Journal of Vegetation Science 12(4):553-66. doi:10.2307/3237007.         [ Links ]

Riesch H. 2010. Simple or simplistic? Scientists' views on Occam's razor. Theoria 25(1):75-90. doi: http://www.redalyc.org/html/3397/339730811005/.         [ Links ]

Rivera L.W., J.K. Zimmerman, & T.M. Aide. 2000. Forest recovery in abandoned agricultural lands in a karst region of theDominican Republic. Plant Ecology 148:115-125. doi:10.1023/A:1009825211430.         [ Links ]

Rosindell J., S.P. Hubbell, & R.S. Etienne. 2011. The unified neutral theory of biodiversity and biogeography at age ten. Trends in Ecology and Evolution 26(7):340-348. doi: https://doi.org/10.1016/j.tree.2011.03.024.         [ Links ]

Rosindell J., S.P. Hubbell, F. He, L.J. Harmon, & R.S. Etienne. 2012. The case for ecological neutral theory. Trends in Ecology andEvolution 27(4):203-208. doi: http://dx.doi.org/10.1016/j.tree.2012.01.004.         [ Links ]

Ruiz J. 2009. Ecología de dispersión y reclutamiento de bosqueshúmedos tropicales. Wani Revista del Caribe Nicaragüense 59:19-30. doi: http://revistasnicaragua.net.ni/index.php/wani/article/view/1308/1256.         [ Links ]

Ruiz J., C. Ingram-Flóres, D.H. Boucher, & L.F. Chaves. 2009.Beneficial effect of spider presence on seedling recruitment of the tropical rainforest tree Dypterix oleifera (Fabaceae). Revista de Biología Tropical 57(3):837-846.         [ Links ]

Student. 1908. The probable error of a mean. Biometrika VI(1):1-25. http://seismo.berkeley.edu/~kirchner/eps_120/Odds_n_ends/Students_original_paper.pdf. Acceso 16/11/2017.         [ Links ]

Tirado R., K.A. Bråthen, & F.A. Pugnaire. 2015. Mutual positive effectsbetween shrubs in an arid ecosystem. Scientific Reports5:14710. doi: 10.1038/srep14710.

Volkov I., J.R. Banavar, S.P. Hubbell, & A. Maritan. 2003. Neutral theory and relative species abundance in ecology. Nature 424(6952):1035-1037. doi: 10.1038/nature01883.         [ Links ]

West-Eberhard M.J. 2005. Developmental plasticity and the origin of species differences. Proceedings of the NationalAcademy of Sciences of the United States of America102(suppl.1):6543-6549. doi: 10.1073/pnas.0501844102.         [ Links ]

Wright J.S., H. Zeballos, I. Domínguez, M.M. Gallardo, M.C. Moreno, & R. Ibáñez. 2000. Pouchers alter mammal abundance, seed dispersal, and seed predation in a Neotropical forest. Conservation Biology 14(1):227-239. doi: 10.1046/j.15231739.2000.98333.x.         [ Links ]

 

Fuentes de financiamiento: Asociación Llapis i Llavors (Pencil and Seeds).

Información sobre los autores:

EIG-P, LG y JR-S diseñaron y redactaron el manuscrito. LG y JC garantizaron el rigor de las interpretaciones y explicaciones matemáticas, además de colectar los datos de campo junto a los dos coautores antedichos. MIA-P y MT se enfocaron en la sección concerniente a la distribución normal, brindando ejemplos prácticos. Todos los autores revisaron y aprobaron el manuscrito.

Los autores declaran que no existen conflictos de intereses.

 

*Autor para correspondencia

Email Edgardo I. Garrido-Pérez: edgardoga2@hotmail.com

Email Laura González: laura.gonzalez.claramonte@gmail.com

Email Jairo Cabrera: jairocabrera87@hotmail.com

Email Jamil Rojas-Salvatierra: jamilrojas@outlook.com

Email María I. Arias-Pizarro: miap.1997@gmail.com

Email Mathew Tello: matiutello@gmail.com

 

Presentado: 30/12/2017

Aceptado: 09/05/2018

Publicado online: 30/05/2018