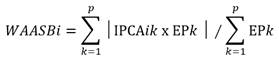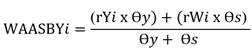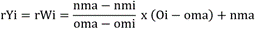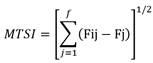1. Introducción
Cuando se desarrollan variedades mejoradas, estas deben alcanzar los máximos rendimientos en los ambientes para los cuales se recomienda su cultivo, para lograr este objetivo se debe seleccionar a los mejores genotipos, una de las formas es mediante el estudio de la interacción genotipo por ambiente (IGA) (Yue et al., 2022; Zystro et al., 2021; Falconer et al., 1996); estudio que permite identificar genotipos estables, es decir, aquellos que tienen la capacidad genética de mantener un rendimiento alto y constante a través de una serie de ambientes y/o condiciones de cultivo (Allard & Bradshaw, 1964; Finlay & Wilkinson, 1963). Sin embargo, esta tarea no es fácil, debido a que el efecto de la IGA es uno de los mayores desafíos en la identificación de cultivares con desempeño estable a través de ambientes y años (Singamsetti et al., 2021), es por ello, que los fitomejoradores se enfocan en evaluar la IGA a través de ensayos en ambientes variables, apropiados e inapropiados (Alwala et al., 2010; Ro et al., 2021).
Dos de los métodos más conocidos para analizar ensayos multiambiente (MET), evaluar la IGA e identificar genotipos superiores son: el efecto principal aditivo y la interacción multiplicativa (Additive main effect and multiplicative interaction, AMMI) (Padmaja et al., 2022) y la mejor predicción lineal insesgada (best linear unbiased prediction, BLUP) (Henderson, 1975). Olivoto et al. (2019) incorporaron los beneficios de estas dos importantes técnicas en un solo método llamado WAASB, que es una nueva medida cuantitativa de estabilidad genotípica y que representa el promedio ponderado de puntuaciones absolutas (Weighted Average of Absolute Scores, WAASB), además, junto a Hussain et al. (2021); Nataraj et al. (2021) y Olivoto et al. (2021) demostraron que el índice de selección simultánea, WAASBY, es útil cuando la selección debe considerar diferentes ponderaciones para la estabilidad y el rendimiento medio.
Si bien, el procedimiento MET mediante AMMI y BLUP generalmente se utilizan para analizar una sola característica a la vez, lo que proporciona una menor confiabilidad en la recomendación de genotipos, en comparación con el método WAASBY que analiza múltiples variables simultáneamente y que ha permitido la selección de genotipos estables. El índice MTSI ha permitido seleccionar genotipos de alto rendimiento y estables en varias especies, por ejemplo: maíz (Yue et al., 2022; Olivoto et al., 2021), avena (Olivoto et al., 2019), lentejas (Sellami et al., 2021), soja (Abdelghany et al., 2021; Zuffo et al., 2020; Nataraj et al., 2021), garbanzo (Hussain et al., 2021), yuca (León et al., 2021), Cymopsis tetragonoloba L. (Benakanahalli et al., 2021), arroz (Sharifi et al., 2020) y mijo (Padmaja et al., 2022).
Las investigaciones previas sugieren que el MTSI es una herramienta importante para la selección de genotipos superiores basados en datos de múltiples caracteres y ambientes. Por lo tanto, los objetivos de este estudio fueron: 1) estimar la contribución de los ambientes, los genotipos y de la interacción genotipo x ambiente en la variación de 11 características y 2) seleccionar líneas S1 de maíz morado reventón basado en el MTSI.
2. Materiales y métodos
2.1 Ensayos de campo
Tres experimentos fueron instalados: uno en Huánuco, Perú, latitud 09°55′15″, longitud 76°18′35″ y altitud 1986 msnm y dos en La Molina, Lima, latitud: 12°04′55″, longitud: 76°56′53″ y altitud 241 msnm.
2.2 Material Biológico
El material vegetal lo constituyeron 80 líneas S1, los mismos que se obtuvieron por autofecundación en plantas híbridas, las plantas híbridas derivaron de la cruza entre una población con alta frecuencia de pericarpio negro y grano no reventón por otra población de pericarpio incoloro y grano reventón.
2.3 Características de la parcela experimental
Los genotipos (líneas S1) fueron sembrados en parcelas de un surco con 12 plantas; las distancias fueron: 0.8 m entre surcos y 0,35 m entre golpes, se mantuvo dos plantas por golpe que equivale a una densidad poblacional de 71428 plantas/ha. El diseño experimental utilizado fue el de Látice Simple con 80 genotipos y dos repeticiones, las características de las parcelas como los genotipos se mantuvieron invariables en cada uno de los tres experimentos. El experimento de Huánuco se condujo en la campaña mayo - octubre del 2019, mientras que los de La Molina en la campaña junio - diciembre del 2019. En los tres experimentos, el cuidado y manejo agronómico fueron similares a las recomendadas para la producción comercial de maíz morado.
2.4 Variables evaluadas
Volumen de expansión (VE). Treinta gramos de grano fueron colocados en un sobre de papel kraft N° 10 para la cocción. Al final del período de reventado, se midió el volumen de los mismos en una probeta graduada de 500 ml y se calculó el volumen de expansión de acuerdo a la fórmula: VE = ENT#091;volumen de granos reventados / peso inicial (30 g)ENT#093;, modificado de Pordesimo et al. (1990). El método de expansión se ajustó a lo propuesto por Paraginski et al. (2016), la expansión se realizó en un horno microondas (Daewoo, 1000 W, modelo: KOR-32FCB), el tiempo de cocción varió entre 2 y 4 minutos, la expansión se interrumpió cuando hubo un intervalo de tiempo de 5 s entre la expansión de un grano y el siguiente.
Porcentaje de expansión (PE). Se obtuvo de: PE = ENT#091;(total de granos expandidos) / (total de granos tostados)ENT#093;*100.
Pericarpio pigmentado (PP). Después de la cosecha y en cada tratamiento, se contabilizó el total de mazorcas de pericarpio negro y se expresó en porcentaje para el análisis estadístico.
Rendimiento de grano (GY). Se determinó con la siguiente fórmula: RDG = Pc * 0,971 * ID * Fh * Ff * (10000 m2/1,75 m2), modificado de Sayre et al. (2012), donde: Pc = Peso de mazorcas cosechadas por parcela, 0,971 = Factor de contorno, ID = Índice de desgrane (peso de grano/peso de mazorca), 1,75 m2 = Área de la parcela, Fh = Factor de corrección por humedad, ajustado al 14 %, Ff =Factor de corrección por fallas. Fh =ENT#091;(100 - % humedad de cosecha) / (100-14)ENT#093;, Ff = ENT#091;(golpes por parcela - 0,3*fallas por parcela) / (golpes por parcela - fallas por parcela)ENT#093;.
Días a la floración masculina (FM). Se registró la fecha en la que se observó que en más del 50% de las plantas tenían sus panojas con polen en emisión.
Longitud de mazorca (LM). Con una regla milimetrada se midió el largo de cada mazorca desde el extremo inferior al extremo superior.
Humedad de grano (HG). Después del desgrane y previo al tostado, se tomó al azar 100 g de la mezcla de los granos de cada parcela y se determinó la humedad con el equipo Agratronix MT-16 medidor portátil de humedad de grano.
Altura de planta (AP). Se midió en 6 plantas por parcela, tomándose desde la base del tallo hasta la base de la panoja.
Peso de 100 granos (PG). Luego de desgranar todas las mazorcas de cada parcela y mezclarlos, se tomó aleatoriamente 100 granos para luego pesarlos.
Volumen de 100 granos (VG). En los mismos 100 granos que se utilizaron para estimar el peso, se determinó también su volumen mediante el uso de una probeta graduada de vidrio de 20 cc de capacidad.
Tamaño del grano expandido (TG). Se obtuvo de: TGE = ENT#091;(Volumen de granos reventados (ml)) / (Número de granos reventados)ENT#093; * 100.
Análisis estadístico
El análisis de estabilidad de los datos de los tres ensayos se realizó utilizando los índices MTSI y WAASB del paquete metan (Olivoto & Lúcio, 2020) del software estadístico R versión 4.0.4 (2021-12-12) de la R Foundation for Statistical Computing (R Core Team, 2021).
2.6. Análisis de varianza
Se realizó un análisis de varianza individual (ANOVA) para cada ambiente, seguido de un análisis de varianza conjunta de acuerdo con el modelo estadístico siguiente:
Yijk = µ + B / Ejk + Gi + Ej + GEij + εijk
donde Yijk representa el i-ésimo genotipo en el j-ésimo ambiente y el k-ésimo bloque; µ es la media general; B/Ejk corresponde al k-ésimo bloque dentro del j-ésimo ambiente; Gi es el efecto del i-ésimo genotipo; Ej es el efecto del j-ésimo ambiente; GEij es el efecto de la interacción del i-ésimo genotipo con el j-ésimo ambiente; y εijk es el efecto del error experimental.
2.7. Estabilidad genotípica según el promedio ponderado de puntuaciones absolutas
La estabilidad genotípica de cada línea S1 fue cuantificada por el índice WAASB a partir de la descomposición del valor singular de la matriz de las mejores predicciones lineales insesgadas para los efectos IGA generados por un modelo lineal de efectos mixtos (Olivoto et al., 2019), estimado como se indica en la siguiente ecuación:
Donde WAASBi es el promedio ponderado de las puntuaciones absolutas del i-ésimo genotipo, IPCAik es la puntuación del i-ésimo genotipo en el k-ésimo eje del componente principal de interacción (IPCA) y EPk es la cantidad de la varianza explicada por el k-ésimo IPCA. El genotipo con el valor de WAASB más bajo se considera el más estable, mostrando la menor desviación del rendimiento promedio en todos los ambientes (Olivoto et al., 2019).
2.8 Selección simultánea para rendimiento y estabilidad
La selección simultánea por rendimiento y estabilidad medios (mean performance and stability, MPE) se realizó utilizando el índice WAASBY que permite ponderar entre el rendimiento medio (Y) y la estabilidad (WAASB) (Olivoto et al., 2019), se estimó de la siguiente manera:
Donde WAASBYi es el índice de superioridad para el i-ésimo genotipo; rYi y rWi son los valores reescalados (0-100) para la variable respuesta (Y) y la estabilidad (WAASB), respectivamente; y θy y θs son los pesos del rendimiento medio (por ejemplo, rendimiento de grano) y estabilidad (WAASB), respectivamente. Los valores rYi y rWi (Olivoto et al., 2019) fueron estimados de la siguiente manera:
Donde nma y nmi son los nuevos valores máximo y mínimo después del cambio de escala, oma y omi son los valores máximo y mínimo originales, y Oi es el valor original para la variable respuesta o el índice WAASB del i-ésimo genotipo. Los valores de nma y nmi se eligieron de acuerdo con la variable, por ejemplo, se desearon valores más altos para: VE, PP, GY, PE, LM, PG, VG y TG; por lo tanto, nma = 100 y nmi = 0. En otras palabras, el genotipo con la media más alta tenía rYi = 100 después del cambio de escala. Mientras que para HG, FM y AP donde se desean valores más bajos, se usaron nma = 0 y nmi = 100.
2.9 índice de estabilidad de múltiples caracteres MTSI
Para estimar el índice de estabilidad de múltiples caracteres (MTSI) (Olivoto et al., 2021; Olivoto et al., 2019), se utilizó la siguiente ecuación:
Donde MTSI es el índice de estabilidad de múltiples caracteres para el i-ésimo genotipo, Fij es la j-ésima puntuación del i-ésimo genotipo y Fj es la j-ésima puntuación del ideotipo. El genotipo con el MTSI más bajo es, por tanto, más cercano al ideotipo, por lo tanto, tiene un alto rendimiento medio y estabilidad para todas las variables estudiadas.
Tabla 1 Análisis de varianza de once características evaluados en 80 genotipos de maíz morado reventón probados en tres ambientes, periodo 2019
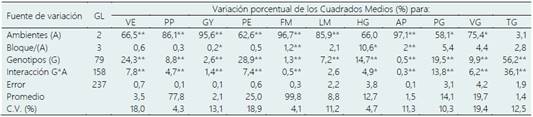
VE, volumen de expansión (cc/g); PP, pericarpio pigmentado (%); GY, rendimiento de grano (t/ha); PE, porcentaje de expansión (%); FM, floración masculina (días); LM, Longitud de mazorca (cm); HG, humedad del grano (%); AP, altura de planta (m); PG, peso de 100 granos (g); VG, volumen de 100 granos (cc); TG, tamaño del grano expandido (cc).
Tabla 2 Índices: de estabilidad genotípica (WAASB), de superioridad (WAASBY) y de estabilidad de múltiples caracteres (MTSI) de 80 genotipos de maíz morado reventón

VE, volumen de expansión; PP, pericarpio pigmentado; GY, rendimiento de grano; PE, porcentaje de expansión; FM, floración masculina; LM, Longitud de mazorca; HG, humedad del grano; AP, altura de planta; PG, peso de 100 granos; VG, volumen de 100 granos; TG, tamaño del grano expandido. ‡ MITSI, índice de estabilidad de múltiples características.
Tabla 3 Eigenvalores, varianzas y magnitudes factoriales después de la rotación varimax obtenidas en el análisis factorial
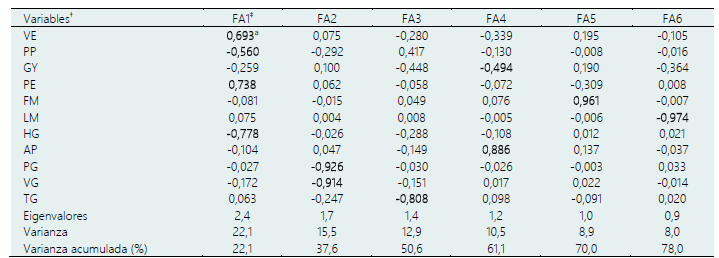
† VE, volumen de expansión; PP, pericarpio pigmentado; GY, rendimiento de grano; PE, porcentaje de expansión; FM, floración masculina; LM, Longitud de mazorca; HG, humedad del grano; AP, altura de planta; PG, peso de 100 semillas; VG, volumen de 100 semillas; TG, tamaño del grano expandido.‡ FA, factor retenido.a Los valores en negrita indican las variables agrupadas dentro de cada factor.
2.10 Estimación de heredabilidad y diferencial de selección
Heredabilidad. La estimación de la heredabilidad en sentido amplio (h2) de todas las características se calcularon de acuerdo con la fórmula descrita por Allard y Bradshaw (1964), de acuerdo a la siguiente ecuación: h2 (Heredabilidad) = ENT#091;(δ2 G) / (δ2 P)ENT#093; × 100, donde: h2 = heredabilidad en sentido amplio; δ2 G = varianza genotípica; δ2 P = Varianza fenotípica.
Diferencial de selección (SD). Se calculó como la diferencia entre la media de los genotipos seleccionados (Xs) y la media de la población antes de la selección (Xo). Es una medida de la superioridad fenotípica de los padres seleccionados sobre la población de la que se seleccionaron los padres (Falconer et al., 1966).
3. Resultados y discusión
3.1. ANOVA para once variables en 80 líneas S1 de maíz morado reventón
El análisis de varianza combinado detectó diferencias estadísticas significativas entre ambientes para 9 de 11 características, las diferencias entre genotipos se observaron en todas las variables y en 10 de 11 características hubo interacción genotipo x ambiente (Tabla 1). El análisis evidenció que las diferencias ambientales contribuyeron en mayor medida a la variación porcentual para todas las variables, los cuales oscilaron entre 58,1% (PG) y 97,1% (AP), excepto para TG; diferencias genotípicas altamente significativas se observaron en todas las características y sus contribuciones porcentuales variaron entre 0,5% (AP) y 56,2% (TG) y finalmente, hubo diferencias estadísticas para la interacción Genotipo x Ambiente en 10 de 11 variables, los cuales oscilaron entre 0,3% (AP) y 36,1% (TG), excepto para LM (Tabla 1). La interacción genotipo x ambiente detectada es indicativo de que el comportamiento de los genotipos fue diferente en los ambientes probados, es decir los genotipos que sobresalen en un ambiente, no necesariamente lo hacen en otro u otros ambientes; es por ello que Singamsetti et al. (2021) mencionan que la IGA es uno de los mayores desafíos en la identificación de cultivares con desempeño estable a través de ambientes y años, a lo que Sellami et al. (2021) adicionan que la IGA es común en ensayos multiambientes.
3.2 Respuesta promedio y estabilidad de genotipos
Según el promedio ponderado de las puntuaciones absolutas (WAASB), el comportamiento de los genotipos fue variable, tanto para una característica como entre características (Tabla 2), lo que confirma la interacción genotipo x ambiente encontrado en el análisis de varianza combinado. De acuerdo con Olivoto et al. (2019), el genotipo con el valor de WAASB más bajo se considera el más estable, de manera que para VE el genotipo más estable fue la línea 41 cuyo valor WAASB fue 0,03, para PP el genotipo más estable fue la línea 238 cuyo valor WAASB fue 0,19, para GY el genotipo más estable fue la línea 109 cuyo valor WAASB fue 0,02, para PE el genotipo más estable fue la línea 130 cuyo valor WAASB fue 0,06, para FM el genotipo más estable fue la línea 27 cuyo valor WAASB fue 0,04, para LM el genotipo más estable fue la línea 216 cuyo valor WAASB fue 0,02, para HG el genotipo más estable fue la línea 77 cuyo valor WAASB fue 0,00, para AP el genotipo más estable fue la línea 111 cuyo valor WAASB fue 0,00, para el PG el genotipo más estable fue la línea 32 cuyo valor WAASB fue 0,05, para VG el genotipo más estable fue la línea 244 cuyo valor WAASB fue 0,01 y finalmente, para TG el genotipo más estable fue la línea 35 cuyo valor WAASB fue 0,01 (Tabla 2); valores similares fueron reportados por Abdelghany et al. (2021) y Sharifi et al. (2020). En todas las características, ningún genotipo resultó ser estable para más de un atributo, lo que confirma la necesidad de buscar una metodología que permita estimar el valor de estabilidad de manera conjunta para múltiples caracteres en forma de índice.
El mismo comportamiento se observó para la selección simultánea por rendimiento y estabilidad medios o índice de superioridad (WASSBY), aunque con genotipos distintos debido a que este pondera el rendimiento medio (Y) y la estabilidad (WAASB) (Olivoto et al., 2019). Es decir, para VE el genotipo más estable fue la línea 30 porque su valor WAASBY fue 4,5, para PP el genotipo más estable fue la línea 48 porque su valor WAASBY fue 27,4, para GY el genotipo más estable fue la línea 141 porque su valor WAASBY fue 5,3, para PE el genotipo más estable fue la línea 167 porque su valor WAASBY fue 21,2, para FM el genotipo más estable fue la línea 32 porque su valor WAASBY fue 20,5, para LM el genotipo más estable fue la línea 141 porque su valor WAASBY fue 20,0, para HG el genotipo más estable fue la línea 79 porque su valor WAASBY fue 15,1, para AP el genotipo más estable fue la línea 2 porque su valor WAASBY fue 22,6, para PG el genotipo más estable fue la línea 115 porque su valor WAASBY fue 14,6, para VG el genotipo más estable fue la línea 218 porque su valor WAASBY fue 7,2 y finalmente, para TG el genotipo más estable fue la línea 169 porque su valor WAASBY fue 26,8, resultados similares fueron reportados por Hussain et al. (2021) y Nataraj et al. (2021).
3.3 Análisis factorial y selección de genotipos basada en el índice MTSI
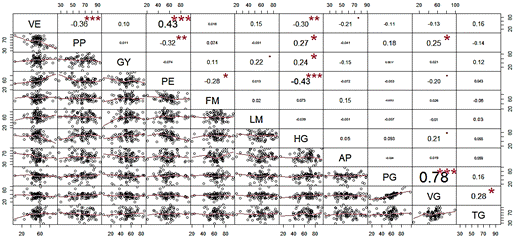
Para saber si algunos de las once características evaluadas están correlacionados y por lo tanto pueden agruparse en un factor común, se realizó un análisis de correlación que se presenta a continuación. En la Figura 1 se observa una matriz de correlación de Pearson para los valores WAASBY, en ella se observan correlaciones significativas entre VE PE; PP, HG y VG; GY y HG; PG y VG; VG y TG, lo que sugiere que estas características pueden agruparse en un factor común. Se observó una asociación negativa entre PE y HG, que se explica por el valor de nma y nmi utilizado para reescalar la variable HG. Para esta variable, los genotipos con un valor WAASBY más alto presentan la HG más bajo y consecuentemente un PE más alto, tal como se aprecia en la Tabla 2.
El análisis de componentes principales mantuvo los seis primeros, los cuales lograron una varianza acumulada del 78% (Tabla 3). Los valores de WAASBY de cada uno de los 11 caracteres se agruparon en los seis factores (FA) de la siguiente manera: FA1, VE, PP, PE y HG; FA2, las variables relacionadas con la semilla PG y VG; FA3, relacionado con el TG; FA4, los rasgos relacionados con GY y AP; FA5, con FM y FA6, con LM (Tabla 3). Con este análisis factorial fue posible reducir de 11 variables a 6 factores que representan una disminución del 45,5%. Aparentemente, no existe relación entre el número de variables analizadas y el número de factores generados, por ejemplo, Hussain et al. (2021) evaluaron 16 variables, generaron 9 factores los que explicaron el 53,8% de la varianza acumulada; del mismo modo, Olivoto et al. (2019) evaluaron 14 variables, generaron 5 factores los que explicaron el 83,0% de la varianza acumulada.
El factor de agrupación uno juntó a cuatro variables VE, PP, PE y HG (Tabla 4), los cuales mostraron estar asociados (Figura 1). El factor 2 agrupó a PG y VG, el factor 4 juntó a GY y AP. Los índices WASBY que presentan valores reescalados entre 0 y 100, permiten calcular las medias de la población original y la de los genotipos seleccionados, de la misma forma, toma en cuenta el sentido de la selección de las variables analizadas (Tabla 1). En este estudio, 8 de 11 variables tuvieron un sentido de selección deseado positivo, es decir más fue mejor y en 6 de 8 se obtuvo un diferencial de selección positivo; mientras que, en 3 de 11 caracteres, el sentido de selección fue negativo, es decir, menos fue mejor, de ellas, en 1 de 3 se obtuvo una media de los genotipos seleccionados menor al de la población inicial y un diferencial de selección negativo. En promedio, el valor de la selección diferencial (Tabla 4) para las variables con selección positiva fue del 10,63% y para las variables con sentido negativo fue de 7,39%, lo cual es indicativo de que aplicando la metodología del índice de estabilidad de caracteres múltiples permite ganancias por selección en el sentido deseado.
La heredabilidad es la relación entre la varianza genética y la varianza fenotípica y varía de 0 a 1. De acuerdo con la Tabla 4, los valores de heredabilidad variaron entre 0,29 para peso de grano (PG) y 0,74 para porcentaje de expansión (PE). La heredabilidad para cinco caracteres superó el valor de 0,5, lo cual es considerado alto, estos fueron PE, VE, HG, LM y FM con valores de 0,74, 0,68, 0,67, 0,65 y 0,64, respectivamente, esto significa que, en promedio, más de la mitad de las diferencias fenotípicas se debieron a causas genéticas. Las demás características presentaron heredabilidad moderada, los cuales oscilaron entre 0,29 para peso de grano (PG) y 0,46 para pericarpio pigmentado (PP) y rendimiento de grano (GY). Valores de heredabilidad altos fueron reportados por Zuffo et al. (2020) y Abdelghany et al. (2021), quienes encontraron valores muy superiores al reportado en esta investigación, esto posiblemente se debe a que tanto los genotipos y las características evaluadas eran distintas a las de este trabajo.
Figura 1. Matriz de correlación de Pearson para los índices WAASBYi de 11 caracteres. *, **, y *** representa significancia al 0,05, 0,01 y 0,001, respectivamente.
Tabla 4 Diferencial de selección del índice WAASBY y heredabilidad para 11 caracteres de maíz morado reventón
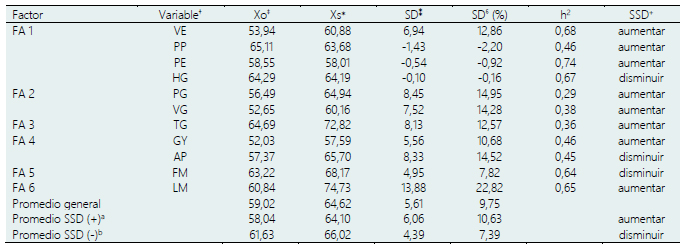
† VE, volumen de expansión; PP, pericarpio pigmentado; GY, rendimiento de grano; PE, porcentaje de expansión; FM, floración masculina; LM, Longitud de mazorca; HG, humedad del grano; AP, altura de planta; PG, peso de 100 semillas; VG, volumen de 100 semillas; TG, tamaño del grano expandido.‡ Xo, media del índice WAASBY de la población original⁎ Xs, media del índice WAASBY de los genotipos seleccionados (64, 56, 41, 112, 152, 212, 117, 249, 126, 86, 216 y 27)⁑ SD, selección diferencial y ⸹ SD en porcentajeh2, heredabilidad en sentido amplio+ SSD, sentido de selección deseadoa, promedio de los caracteres cuyo sentido de selección deseado fue hacia el aumentob, promedio de los caracteres cuyo sentido de selección deseado fue hacia la disminución.
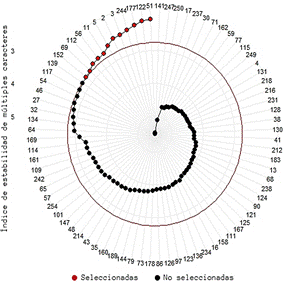
El índice MTSI es un método fácil y rápido para identificar genotipos rendidores y estables (Olivoto et al., 2019). La Figura 2 muestra la clasificación de genotipos de acuerdo con el índice MTSI, en ella se observa que se identificaron 12 líneas S1 que representa una presión de selección del 15%; estos genotipos fueron 64, 56, 41, 112, 152, 212, 117, 249, 126, 86, 216 y 27, con valores MTSI de 4,10, 5,11, 5,14, 5,17, 5,39, 5,43, 5,53, 5,57, 5,65, 5,84, 5,88 y 5,89, respectivamente. Estas líneas son consideradas como los más estables dentro del grupo de los 80 genotipos evaluados en este trabajo de investigación. El MTSI de 5,89 sirvió como punto de corte (Figura 2, círculo rojo), valores iguales o inferiores fueron los más estables.
Figura 3. Clasificación de líneas S1 de maíz morado reventón según el índice de estabilidad de múltiples caracteres. Genotipos seleccionados (círculo rojo) y genotipos no seleccionados (círculo negro).
El MTSI está siendo cada vez más utilizado, en esta investigación permitió seleccionar líneas promisorias de maíz morado reventón, tal como lo hicieron Benakanahalli et al. (2021) en Cymopsis tetragonoloba; Olivoto et al. (2019) en Avena sativa; Yue et al., 2022 y Olivoto et al. 2021 en híbridos de maíz; Sharifi (2020) en arroz; Nataraj et al. (2021) en soya; Hussain et al. (2021) en garbanzo; Zuffo et al. (2020) y Abdelghany et al. (2021) en soya; Sellami et al. (2021) en lentejas y Padmaja et al. (2022) en mijo.
4. Conclusiones
Los resultados indicaron que las diferencias ambientales contribuyeron en mayor medida a la variación total, seguido de las diferencias genotípicas; ambos fueron significativos para todas las variables, además, la interacción genotipo x ambiente fue significativo en 10 de 11 características evaluadas. De acuerdo con el índice de estabilidad de múltiples caracteres (MTSI) y con una presión de selección del 15%, 12 líneas S1 de maíz morado reventón fueron seleccionados como las más estables y de alto rendimiento entre los 80 genotipos evaluados, estas fueron 64, 56, 41, 112, 152, 212, 117, 249, 126, 86, 216 y 27. Las líneas S1 seleccionadas serán convertidas en líneas dobles haploides y evaluadas por sus habilidades combinatorias general y especifica.