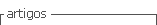INTRODUCCIÓN
El síndrome respiratorio agudo grave, coronavirus 2 (SARS-Cov-2) es un agente viral contagioso que surgió en la ciudad de Wuhan (provincia de Hubei) en China.
Esta fue catalogada oficialmente el 31 de diciembre de 2019, y es responsable de la comúnmente llamada: pandemia del Covid -19 (enfermedad causada por el SARS-Cov-2), que al 20 de junio del 2020 se tiene 8 921 618 casos confirmados en todo el mundo [1]. De acuerdo a la Organización Mundial de la Salud (OMS) y el MINSA, los síntomas más comunes son tos seca, disnea, fiebre, ageusia y anosmia [1][2]. Hasta la elaboración de este artículo no se tenían medicamentos específicos para el tratamiento de esta enfermedad [1].
Diversas medidas preventivas y de contingencia fueron tomadas por los gobiernos para frenar el avance de la pandemia, tales como: higiene, uso de mascarilla, aumento del número de trabajadores de la salud, medidas de aislamiento social, adquisición de suministros como pruebas y remedios no específicos para esa enfermedad, entre otros, recomendadas por OMS [1][3][4]. Países como Italia y España, que previamente presentaron un grande crecimiento de infectados en marzo del 2020, anunciaron la disminución de las restricciones, después de alrededor de 3 meses de haber acatado medidas estrictas como la cuarentena [5].
En América del Sur, al 20 de junio de 2020 se tiene 1.746.976 casos confirmados de Covid-19, lo que corresponde al 19,6% en todo el mundo. Perú tiene 251 338 casos (2,8% en el mundo y 14,4% en América del Sur) mostrando un gran aumento incluso después de 120 días de restricción social obligatoria [1]. En algunas regiones como Lima, Loreto, Chiclayo han informado una situación de colapso en sus sistemas de salud [6][7]. Esto implica evaluar la efectividad de las medidas tomadas hasta el momento, especialmente con respecto al aislamiento social, que ha sido adoptado con menos de 100 casos confirmados [8].
El análisis predictivo tiene como objetivo evaluar y proyectar la evolución del número de casos confirmados de Covid-19 en el Perú hasta fines del año 2020, basada en el modelo no lineal de Gompertz, el cual permite la predicción del número contagiados y casos fatales en las próximas semanas y/o meses. Proporcionalmente se puede estimar el número pacientes que serán atendidos en los hospitales. De esta manera, la administración de recursos puede hacer los requerimientos correspondientes para la adquisición de equipos o insumos. Asimismo, es de suma importancia saber la tendencia de los contagios a largo plazo, dado que esa información puede servir para tomar decisiones respecto al grado de las medidas de aislamiento.
METODOLOGÍA
2.1 MODELOS MATEMÁTICOS
En las ciencias aplicadas, un modelo matemático es un tipo de modelo científico que emplea fórmulas matemáticas para expresar relaciones, variaciones, variables, etc. Con lo que se puede estudiar el comportamiento de sistemas complejos en situaciones difíciles de proyectar o pronosticar [9][10].
Existen diversos modelos que pueden ser usados para analizar los datos de la pandemia del Covid-19. Estos modelos dependen de diversas variables y pueden ser utilizados de acuerdo a la información requerida. El tiempo es una de las variables principales, por esta razón es posible obtener comportamientos y tendencias de la evolución del covid-19. Entre los modelos más comunes se tienen las funciones empíricas, estadísticas y dinámicas [11][12].
En la etapa inicial de una epidemia ningún modelo es confiable para realizar predicciones a largo plazo, debido a que la cantidad de datos es mínima. En esas circunstancias, los modelos complejos pueden sobreestimar o subestimar el futuro real de una epidemia. Por lo tanto, en fases iniciales, se recomienda usar modelos con menos parámetros, como la función exponencial o incluso una función lineal, no obstante, estas predicciones son a corto plazo [11][13].
En las etapas media y tardía de la epidemia, las funciones sigmoideas son las más adecuadas para el análisis predictivo de fallecidos y contagiados, etc [11][12]. Algunas de esas, son las funciones Logística, Gompertz y Richards, las cuales pueden capturar la curva en forma de ‘S’, típica para los datos acumulativos. Entre las funciones sigmoideas, la función de Gompertz es la que mejor se ajusta a la evolución de casos de covid-19 [11][12][14].
2.2 MODELO DE GOMPERTZ
La curva o función de Gompertz, es un tipo de modelo matemático para una serie temporal, creado por Benjamin Gompertz (1779-1865). Es una función sigmoidea que describe el crecimiento lento desde el inicio hasta el fin de un período de tiempo dado. El modelo se puede representar de la siguiente manera [12][13]:

Donde: P define el número de casos confirmados de Covid-19 en un momento dado t (días); c es el tamaño asintótico o el número máximo de casos confirmados; b y a es números positivos; b establece el desplazamiento a lo largo del eje t; a establece la tasa de crecimiento y e es el número de Euler [15].
2.3 AJUSTE DE CURVAS
En este estudio será usado el método de mínimos cuadrados no lineales para el ajuste de la curva y se puede definir como:
Dados los pares ordenados, estimar los parámetros 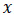 que definen una función no lineal
que definen una función no lineal 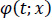 , suponiendo que [16]:
, suponiendo que [16]:
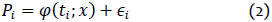
Donde 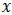 representa a los errores de medición.
representa a los errores de medición.
En la estimación de mínimos cuadrados se busca 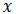 como la solución del siguiente problema de optimización [16][17]:
como la solución del siguiente problema de optimización [16][17]:
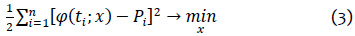
Desde el punto de vista probabilístico, se sabe que la solución de mínimos cuadrados es la estimación de máxima verosimilitud, siempre que todos 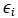 sean variables aleatorias independientes y normalmente distribuidas. El algoritmo para calcular los mínimos cuadrados no lineales está implementado en diferentes herramientas matemáticas como Matlab, Scipy, etc. Los cuales fueron usados en este trabajo.
sean variables aleatorias independientes y normalmente distribuidas. El algoritmo para calcular los mínimos cuadrados no lineales está implementado en diferentes herramientas matemáticas como Matlab, Scipy, etc. Los cuales fueron usados en este trabajo.
Las métricas de ajuste calculadas en este trabajo son:
(a) el coeficiente de determinación R2, que refleja la bondad del ajuste de un modelo a la variable que pretender explicar;
(b) el error cuadrático medio (RMSE) mide la cantidad de error que hay entre dos conjuntos de datos. Es decir, compara un valor de la predicción y un valor observado o conocido [18].
2.4 DATOS Y VARIABLES
Existen muchos datos reportados sobre la pandemia del Covid-19, entre los más utilizados se tienen las frecuencias absolutas y/o acumuladas de: casos confirmados, fallecidos y recuperados. Estos datos, son proporcionales entre sí, la proporcionalidad más conocida es la tasa de letalidad. Otros datos, probablemente menos mencionados, son el número de personas en UCI y el número de personas con oxígeno. Para el caso en análisis fueron usados datos proporcionados por el MINSA desde el 6 de marzo al 20 de junio del año 2020 [2].
En el modelo de Gompertz son necesarios las frecuencias acumuladas y estas pueden ser: (1) casos acumulados de infectados (CAI) o (2) casos acumulados fatales (CAF). En este trabajo se utilizó los datos de casos fatales porque presentan mayor confiabilidad respecto a la de casos confirmados por pruebas, dado que muchas personas contagiadas no se realizan la prueba, por ser asintomáticos u otras causas.
Para poder estimar la curva CAI, a partir de la curva CAF, son necesarias conocer la tasa de letalidad y el desfase de los días entre los incidentes que generan estas curvas, es decir entre el día de confirmación del caso y el día del fallecimiento.
2.5 DESFASE DE DÍAS ENTRE INCIDENTES DEL COVID-19
En la Figura 1 se muestra una línea de tiempo donde se tiene, el día que sucedió el contagio (DC), día de inicio de síntomas (IS), día que se confirma el contagio (CC) y día del fallecimiento (DF), estos estarán desfasados en días como se muestra en la Figura 1.
Esa cantidad de días entre cada incidente son aproximadas y están basadas en datos promedios reportados [19]. Por ejemplo, el promedio de 8 días entre DC y CC es porque se tiene 5 días desde DC hasta IS [20] y 3 días desde IS hasta CC, debido a la demora de los resultados de las pruebas [21].
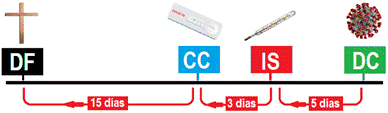
La Figura 2 muestra una curva normalizada de casos diarios, que están sobrepuestas para una misma fecha. Las posiciones de los incidentes en la curva también estarían desfasadas, como se muestra en la Figura 1. Por ejemplo, si DF estaría pasando por el pico, DC estarían en descenso.
Si fueran realizadas curvas para cada incidente, estas serían de diferentes, sin embargo, serían proporcionales. Por ejemplo, se puede encontrar la curva de infectados diarios a partir de la curva de casos fatales diarios, sabiendo el valor de desfase en días entre las incidencias y el valor de la tasa de letalidad.
2.6 ESTIMACIÓN DE LA TASA DE LETALIDAD
La OMS cita el 3,4% (a nivel global) como la tasa de letalidad por el covid-19 (% de personas que fallecen después del contagio) [1]. No obstante, el valor más aproximado de la tasa de letalidad será aquella que se calcule al final de la pandemia, cuando se tenga la cantidad completa de fallecidos e infectados. Por lo tanto, la estimación de esa tasa de letalidad dada por la OMS está fuera de contexto.
Las fórmulas (1) y (2) son normalmente usados para para calcular la tasa de letalidad durante el transcurso de una epidemia.
(1) Tasa de letalidad (%) = [N° fallecidos] x 100/ [Total de contagiados],
(2) Tasa de letalidad (%) = [N° fallecidos] x 100 / [N° Recuperados + N° de fallecidos].
Es probable que (1) sea una subestimación, porque muchos casos contagiados aún pueden terminar en la muerte y no ser contabilizados. La (2) es una sobrestimación, porque es probable que las muertes se den antes que muchos casos recuperados sin ser contabilizados, o sea la recuperación de pacientes puede demorar más que el fallecimiento. Esas fórmulas pueden ser representadas como dos funciones dependientes del tiempo, a medida que la pandemia sea controlada estas funciones tenderán a un mismo valor, el cual sería la tasa de letalidad más real [22]. Otra forma de calcular la tasa de letalidad más próxima de la real es usando la fórmula:
(3) Tasa de letalidad (%) = [N° Muertes] x 100/ [Total de contagiados hace ‘’X’’ días]
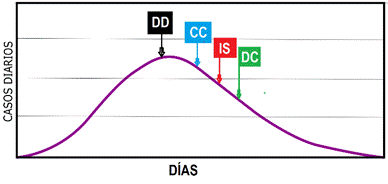
El comportamiento del resultado de la ecuación (3), cuando X=15, es mostrada en la Figura 3.
La fórmula (3) no toma en cuenta aquellos contagiados de los últimos 15 días, porque se desconoce cómo terminarían esos casos. De esa manera, el valor de la tasa de letalidad será aproximadamente 3.5%, este es un valor referencial y puede variar durante el transcurso de la pandemia.
RESULTADOS
Esta sección presenta los resultados obtenidos por el algoritmo del ajuste de la curva de Gompertz con los datos de CAF.
3.1 PARÁMETROS Y MÉTRICAS
La Tabla 1 muestra los valores obtenidos para el modelo de Gompertz de la , así como las métricas de ajuste de los datos.
3.2 PREDICCIÓN DE LA CURVA DE CASOS ACUMULADOS
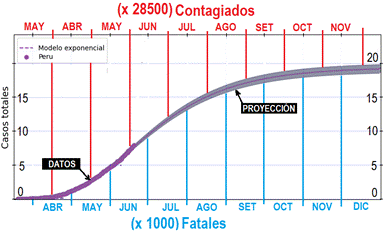
La Figura 4 muestra una curva normalizada proporcional a la CAI y a la CAF. Esta fue obtenida utilizando datos hasta el 20 de junio, desde donde se muestra la proyección a futuro.
En el gráfico se observan dos ejes horizontales temporales (superior e inferior desfasados en 15 días según el análisis de la sección 2.5). El eje horizontal superior es usado para estimar la curva CAI y El eje horizontal inferior es usado para estimar la curva CAF.
Para obtener los valores del eje vertical correspondientes a CAI y CAF son multiplicados por las constantes C1=28 500 y C2=1 000, respectivamente. La constante C1 fue obtenida usando como proporción la tasa de letalidad en función de la cantidad de infectados, obtenida en la sección 2.6 y C2 fue calculada de la normalización de CAF.
Usando el eje horizontal superior correspondiente a CAI, se observa lo siguiente:
La curva se mantendría constante a partir de octubre, dado que a partir de esa fecha se tendría pocos casos confirmados por día.
La curva presenta una tendencia de alcanzar unos 550 mil casos confirmados hasta fines de noviembre.
La cantidad de infectados aproximada para el 20 de junio sería 10 x 28500 = 285 000, estando próximo al valor oficial del MINSA, que es de 251 338. Este resultado muestra que se tendría más contagiados que los reportados oficialmente.
Usando el eje horizontal inferior correspondiente a CAF, se observa lo siguiente:
La curva presenta una tendencia de alcanzar unos 19 000 fallecidos hasta fines de noviembre y
La curva tendrá una tendencia horizontal a partir de fines de octubre, dado que se tendría una mínima cantidad de fallecidos diarios.
3.3 PREDICCIÓN DE LA CURVA DE EPIDÉMICA
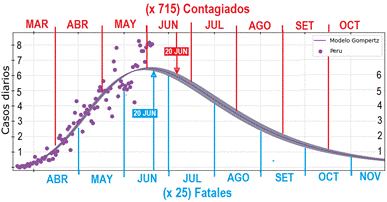
La Figura 5 muestra una curva proporcional a la curva de fallecidos por día y a la curva epidémica. La cual fue obtenida a partir de la derivada de primer orden de la curva acumulada de casos de la Figura 4. La dispersión de puntos que se muestra alrededor de la línea de tendencia son los datos oficiales de casos fatales diarios. En este gráfico, también se tienen dos ejes horizontales temporales (superior e inferior desfasados en 15 días según al análisis de la sección 2.5).
El eje horizontal superior es usado para (1) la curva epidémica estimada y el eje horizontal inferior es usada para (2) la curva de casos fatales diarios. Para obtener los valores del eje vertical son multiplicados por las constantes C3=715 y C4=25 para el caso (1) y (2), respectivamente. La constante C3 fue obtenida usando la proporción de la tasa de letalidad en función de la cantidad de infectados, obtenida en la sección 2.6 y C2 fue calculada de la normalización de la curva de casos fatales por día.
El eje horizontal superior corresponde a la curva epidémica, la cual estaría en un descenso gradual lento. Esto sería más notorio en la última semana de junio, debido a que los datos oficiales reportados presentan una alta dispersión. La cantidad de contagios por día disminuiría considerablemente para inicios de setiembre.
El eje horizontal inferior corresponde a la curva de casos fatales diarios, se observar que la curva de casos fatales por día estaría pasando por la meseta y la última semana de junio se notaría un descenso. Para fines de octubre se tendría pocos fallecidos por día, presentando una tendencia de disminuir aún más.
DISCUSIONES Y CONCLUSIONES
La predicción de casos confirmados en función de datos de casos fatales puede presentar mayor confiabilidad en comparación con la predicción usando datos de casos confirmados mediante pruebas. Debido a la falta de uniformidad e ineficiencia en las pruebas, existencia de casos asintomáticos, demora de la entrega de resultados, entre otros.
Las funciones sigmoideas, así como la de Gompertz son comúnmente utilizados para predecir la tendencia de los contagios a futuro. Para el caso del Perú usando los datos de CAF, el modelo de Gompertz se ajusta con precisión, presentando un coeficiente de determinación R2=0,9987.
Las predicciones de las secciones 3.2 y 3.3 han sido realizadas en base a los datos oficiales reportados hasta el día 20 de junio. Posteriormente, si la población mantiene su comportamiento sin grandes alteraciones, la curva mantendrá su tendencia. Caso contrario, los casos podrían aumentar, generando una nueva onda de contagios. En el mejor de los casos, si las medidas preventivas son más eficientes, o si en un futuro muy próximo se encuentran medicamentos específicos para el Covid-19, se daría un descenso acelerado de la curva.
La predicción de la curva de casos acumulados muestra, por el momento, una tendencia que el Perú alcanzará unos 550 mil infectados y unos 19 mil fallecidos, hasta fines del año 2020.
La predicción de la curva epidémica o de contagiados por día, presenta que la misma estaría en un descenso después de haber atravesado por la meseta, estimada entre la última semana de mayo y la primera quincena de junio. Por otro lado, la curva de casos fatales diarios muestra que estaría atravesando por una meseta y la primera semana de julio ya se notaría un descenso. La tendencia también muestra que en octubre, los casos fatales se reducirían a menos de 25 por día e iría descendiendo aún más.
El análisis del pico de la curva epidémica concuerda con los resultados publicados por Centro Nacional de Epidemiología, Prevención y Control de Enfermedades del MINSA [24]. A partir de los datos tomados desde el inicio de los síntomas de los pacientes, los cuales muestran un descenso de los contagios.
Actualmente, el Perú se encuentra en una etapa avanzada de la pandemia, el análisis realizado con los datos totales muestran una situación global de las predicciones en el país. Un análisis similar para regiones con gran cantidad de contagios podría mostrar una situación más focalizada, dado que el modelo de Gompertz es más confiable en etapas intermedias y avanzadas de la epidemia.
Por lo cual, se debe entender que los resultados de los modelos matemáticos, son para tomar medidas de contingencia. Para que las predicciones, en caso de ser catastróficas, no se cumplan. Esas contingencias pueden ser, por ejemplo: cantidad de camas de UCI para períodos futuros, cantidad de medicamentos por fases, periodos de aislamiento social obligatorio, fechas de reactivación económica, entre otros.