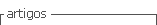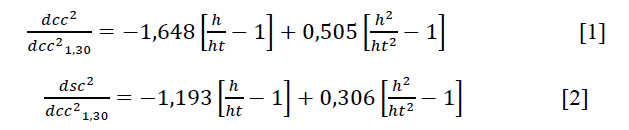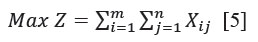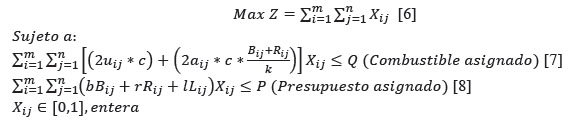Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO  uBio
uBio
Compartilhar
Arnaldoa
versão impressa ISSN 1815-8242versão On-line ISSN 2413-3299
Arnaldoa vol.25 no.2 Trujillo mayo/ago. 2018
http://dx.doi.org/http://doi.org/10.22497/arnaldoa.252.25215
ARTÍCULOS ORIGINALES
Modelación del raleo mediante el uso de la Programación Lineal en plantaciones de Pinus caribaea Morelet de la Empresa Agroforestal Pinar del Río, Cuba
Modeling of Thinning Through the Use of Linear Programming in Pinus Caribaea Morelet Plantations from the Agroforestry Company of Pinar del Río, Cuba
Bertha Rita Castillo Edua1, Zhofre Aguirre Mendoza2
1 Docente-Investigador. Depar tamento de Ciencias Forestales, Universidad de Pinar del Río (UPR). Calle Martí # 270 final. Pinar del Río
2 Docente-Investigador de la Universidad Nacional de Loja, Ecuador. Autor para correspondencia: bertharita1972@gmail.com
Resumen
La investigación tuvo como propósito modelar el raleo en plantaciones de Pinus caribaea Morelet var. caribaea Barret y Golfari, utilizando la Programación Lineal como herramienta matemática y considerando como restricciones económicas el presupuesto y el combustible asignado a la empresa. Para ello se trabajó con datos obtenidos del Proyecto de Ordenación de la Unidad Silvícola San Juan y Martínez, perteneciente a la Empresa Agroforestal Pinar del Río. La muestra se seleccionó a partir de los rodales que tenían manejo recomendado. El modelo matemático obtenido, planifica los raleos en un total de 30 meses con las cantidades óptimas de combustible y presupuesto a emplear para ello, de modo que se maximice el número de rodales a ralear en la Unidad Silvícola. Considerando los resultados del modelo, la actividad se realizaría en dos años y seis meses, con un consumo total de 973,2 litros de combustible y $ 298 708,74 de presupuesto. Además, ordena los rodales que debe recibir el tratamiento silvicultural, mostrando el tipo de raleo y el orden del mismo, de modo que se optimice la actividad forestal.
Palabras clave: modelamiento forestal, tratamiento silvicultural, programación lineal, plantaciones de Pinus caribea.
Abstract
The purpose of the research was to model thinning in plantations of Pinus caribaea Morelet var. caribaea Barret and Golfari, using Linear Programming as a mathematical tool and considering the budget and fuel assigned to the company as economic constraints. For this, we worked with data obtained from the San Juan y Martínez Silvicultural Unit Management Project, which belonging to the Pinar del Río Agroforestry Company. The sample was selected from the stands that had recommended management. The mathematical model obtained, plan the thinning in a total of 30 months with the optimal amounts of fuel and budget to be used for it, so as to maximize the number of stands to thin in the Silvicultural Unit. Considering the results of the model, the activity would be carried out in two years and six months, with a total consumption of 973.2 liters of fuel and $ 298 708.74 of budget. In addition, it orders the stands that should receive the silvicultural treatment, showing the type of thinning and the order of them, so that the forestry activity is optimized.
Keywords: forest modeling, silvicultural treatments, linear programming, plantations of Pinus caribea
Introducción
El patrimonio forestal en Cuba es de 3 934,17 m3/ha, de las que 150,03 m3/ha pertenecen a plantaciones jóvenes y 530,74 m3/ ha representan las plantaciones existentes en el país. Los incrementos provenientes de las plantaciones forestales son generalmente muy bajos (<7 m3/ha/año) así como, la proporción de diámetros superiores y las disponibilidades de madera de dimensiones aserrables. Más del 70 % del total de los bosques productores tienen clases diamétricas menores de 16 cm (Herrero, 2015).
El Programa de Desarrollo Forestal hasta el 2020 tiene una marcada incidencia en la ejecución de los tratamientos silviculturales y para lograr el rendimiento óptimo de las plantaciones se necesita la ejecución del programa de raleos con un estricto control, tanto en la calidad del trabajo como en el calendario correspondiente a las exigencias técnicas de los mismos (Castillo, 2015).
Dado lo anterior, en la presente investigación se utiliza la programación matemática como herramienta para optimizar la actividad de raleo, con el propósito de garantizar plantaciones de mejor desarrollo productivo, de manera tal que se logre incrementar los rendimientos de la especie.
Los modelos de optimización contribuyen a predecir los efectos económicos que va a tener una intervención silvícola a largo plazo, en lo referente a la producción de madera y a las características que tendrá el propio bosque. Además sirven de herramientas para investigar acerca de la dinámica forestal (Abellanas et al. 2009), siendo la programación lineal una de las técnicas más aplicadas a los problemas de toma de decisiones (León, 2008).
Pinus caribaea var. caribaea Morelet Barret y Golfari es una de las especies forestales de mayor importancia debido a los usos que se hace de su madera, siendo una de las priorizadas en los planes de reforestación en la región occidental y central de Cuba hasta el año 2020. No obstante a ello, el incumplimiento de los planes de manejo provoca que los raleos no se ejecuten en el momento preciso, obteniéndose bajos rendimientos en los surtidos planificados según los objetivos de las plantaciones (Russo, 2015).
Sin embargo, la insuficiente gestión del raleo de las plantaciones trae consigo la existencia de una excesiva proporción de árboles con diámetros pequeños, provocando la obtención de bajos rendimientos en los surtidos planificados según los objetivos de las plantaciones (Barrero, 2010).
El estudio tuvo como objetivo modelar el raleo en plantaciones de Pinus caribaea Morelet var. caribaea Barret y Golfari, utilizando le Programación Lineal como como herramienta matemática, considerando como restricciones económicas el presupuesto y el combustible asignado a la Unidad Silvícola San Juan y Martínez en la Empresa Agroforestal Pinar del Río.
Materiales y metodos
Para la construcción del modelo de Programación Lineal se tuvieron en cuenta los siguientes elementos propuestos por Felipe et al., (2001).
Construcción de la función objetivo, que representa la meta que el modelo de optimización desea alcanzar. Elaboración del sistema de restricciones referidas a las cantidades de recursos que limitan el cumplimiento de los objetivos. Determinación de la función objetivo indicando que deben utilizarse solamente ecuaciones lineales o desigualdades lineales.
La Unidad Silvícola se encuentra ubicada en la parte centro y sur de la provincia Pinar del Río, limitando geográficamente al norte con los municipios Minas de Matahambre; al sur con el Mar Caribe; al este con el municipio Pinar del Río y al oeste con el municipio Guane (figura 1) (Guelmez y Acosta, 2007).
El patrimonio forestal representa el 44,8 % del área total de la Empresa Forestal Integral Pinar del Río con una superficie del patrimonio forestal de 18 946,0 ha; de ellas 10 908,5 ha cubiertas de bosques, de las que 5 966,0 ha son de bosques naturales y 4 942,0 ha son plantaciones. El área cubierta representa el 26,5 % del área total de la Unidad Silvícola.
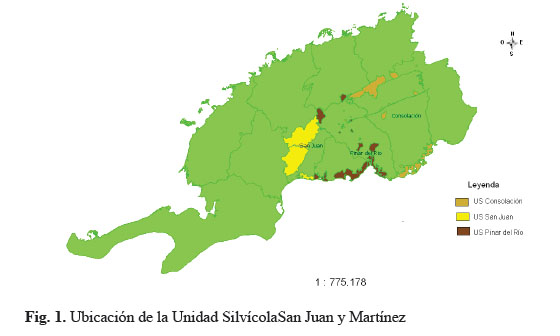
Las plantaciones jóvenes están representadas por 1 019,8 ha. Las áreas desforestadas abarcan 6 611,9 ha, con un área inforestal de 382 ha, según los datos aportados por el Servicio Estatal Forestal en la Provincia obtenidos de la última Dinámica Forestal, con cierre diciembre del año 2016. Se encuentra dividida en 86 lotes y 1 308 rodales. El área promedio por lote es de 220,3 ha y 14,5 ha por rodal predominando las categorías de bosques de producción de pinares y bosques de protección del litoral de manglares, Guelmez y Acosta (2007).
La división del territorio por grupo de edad muestra que un total de 2 453,4 ha (20,6%) se encuentran en la etapa de brinzal; 7 898,5 ha (62,0 %) en la etapa de latizal; 1 689,3 ha (14,2%) pertenecen al fustal adulto y solo 379,8 ha (3,2%) se encuentran en la etapa de fustal maduro. Los índices de sitios más representativos en la entidad son V, VI, VII, VIII, muy desfavorables para el desarrollo de Pinus caribaea var. caribaea. (Guelmez y Acosta, 2007).
En la investigación se trabajó con datos obtenidos del Proyecto de Ordenación del decenio 2006-2016 con la información referida a lote, rodal, ubicación, área, edad, clase de edad, calidad de sitio, grupo de edad, altura media, diámetro medio, densidad, número de árboles por hectáreay volumen por hectárea.
ara la selección de la muestra se identificaron según la Norma Ramal 595 y con el SIFOMAP IV de la Empresa Agroforestal Pinar del Río, los rodales con densidades superiores a 0,7 de diferentes edades y calidades de sitios, representando un total de 80 rodales que pertenecen a 41 lotes y que tenían manejo recomendados, según el proyecto de ordenación de la Unidad Silvícola.
La determinación de los surtidos de los árboles raleados se estimó a partir de la tabla de volumen elaborada por Gra et al. (1990) y los modelos de perfil del fuste de diámetro con corteza (dcc) y sin corteza (dsc) elaborados por Barrero (2010).
Modelos de perfil de fuste de dcc y dsc (Barrero, 2010)
Para el diagnóstico de la actividad de raleo en relación a la cantidad de rodales según el plan de manejo de la Ordenación Forestal, se realizó un análisis de frecuencia del recuento de los rodales a ralear planificados por la ordenación, así como su estado de cumplimiento para los 80 rodales mediante el procesador estadístico SPSS 21.
El modelo de optimización del raleo se elaboró a partir del empleo de técnicas de elementos de Investigación de Operaciones basados en cinco etapas (Definición del problema, construcción del modelo, solución del modelo, validación del modelo e implantación de los resultados finales).
Definición del problema
El problema se formuló como un modelo de Programación Lineal por las características de esta herramienta que permite resolver problemas que se ajustan a la asignación de recursos a ciertas actividades (Goberna, 2006).
Problema a resolver: actualmente en la Unidad Silvícola los raleos se realizan sin tener en cuenta la planificación recomendada en el proyecto de ordenación, en ocasiones, aquellos rodales que se encuentran en áreas de difícil acceso no reciben la atención en el momento adecuado, por lo que se hace necesario realizar un análisis donde se consideren los recursos fundamentales que afecten dicha selección. Entre estos elementos, la administración de la entidad manifiesta que los más importantes son el combustible y el presupuesto asignados para el cumplimiento de los planes de producción. En ese sentido, el objetivo del modelo consiste en determinar la asignación óptima de recursos que permita maximizar la cantidad de rodales a los que se les pueda aplicar el raleo correspondiente.
Construcción del modelo
El modelo empleado considera los aspectos de interés para realizar el raleo en la Unidad Silvícola, el problema se resuelve con el empleo de una función objetivo de maximización de los rodales a ralear, el resto de los parámetros se controlan a través de un sistema de restricciones, es decir el modelo matemático comprende principalmente tres conjuntos básicos de elementos, estos son:
• Definición de las variables de decisión
• Construcción del sistema de restricciones
• Construcción de la función objetivo
Definición de las variables de decisión
Las variables de decisión se definieron como enteras y binarias (pueden tomar los valores 0 y 1). Cada rodal incluido en el análisis tiene una variable de decisión asociada, cuando es hallada la solución del modelo, si la variable de decisión es igual a cero, significa que el rodal no debe intervenirse aún, cuando toma valor uno, se aconseja ralear el rodal.
El modelo incluye los 80 rodales pertenecientes a 41 lotes. El criterio de selección de la muestra corresponde a los rodales que tienen planificado raleos en el período 2006-2016, según el Proyecto de Ordenación, por lo que, el criterio de selección de la variante óptima es el rodal a ralear, es decir, todos los rodales que tienen densidad mayor o igual a 0,7 teniendo en cuenta la NRAG 595, constituyen las variables de decisión.
El objetivo del modelo es determinar qué rodales ralear de acuerdo al presupuesto y combustible asignados a la Unidad Silvícola en cada mes. De este modo, las variables de decisión representan la elección, o no, del rodal a ralear, por lo que quedarían definidas como:
Este es el caso de un Problema de Programación en Enteros donde las variables de decisión pueden tomar solo valores enteros [
Construcción del sistema de restricciones.
En el modelo se tuvieron en cuenta dos restricciones fundamentales, el presupuesto y el combustible asignados a la Unidad Silvícola para realizar el raleo (I, II, III).
Restricción de consumo de combustible
La primera restricción recoge el gasto de combustible para la aplicación del raleo y la acumulación silvícola. Así, cada camión dará dos viajes (ida y vuelta) desde la Unidad Silvícola hasta el j-ésimo rodal, para trasladar a la brigada, de modo que se tiene en cuenta la distancia desde el rodal hasta la Unidad Silvícola y el consumo de combustible por camión. Además se calcula el gasto de combustible para aquellos rodales de los cuales se extrae madera en bolo o rolliza luego de aplicarle el raleo; por lo que se representa en la restricción el viaje de ida y vuelta realizado desde el aserrío para recoger la madera. La leña no se incluye, pues esta permanece en la plantación y solo se recogerá madera en bolo o rolliza.
De este modo la restricción garantiza que se destine combustible para el raleo de los rodales involucrados en el estudio, así como para la Castillo & Aguirre: Modelación del raleo mediante la Programación Lineal en Pinus caribaea de la Empresa Pinar del Río, Cuba acumulación silvícola de aquellos a los que se les aplica el raleo y tienen como resultado volúmenes de madera en bolo o rolliza o ambos. La asignación de combustible para la actividad es de 690 litros/mes.
Para calcular el volumen estimado de madera en bolo y rolliza a extraer en cada rodal se utilizó la tabla de volumen de surtido y densidad de Pinus caribaea en plantaciones puras, elaborada por el Instituto de Investigaciones Forestales (1990).
Apartir de estos elemento la restricción del consumo de combustible asignado es la siguiente:
Restricción del gasto del presupuesto asignado
La segunda restricción contiene el gasto de presupuesto asociado a la actividad de raleo a partir de los costos promedios estimados para cada tipo: I, II y III respectivamente, proporcionados por la Dirección Económica de la Unidad Silvícola.
Para calcular el costo promedio de extracción de madera en bolo y madera rolliza se multiplicaron estos volúmenes por el costo de transporte de madera en un camión Kraz-257 según Cándano (1998).
El presupuesto mensual destinado a esta actividad es de $12 000,00 (Dirección Económica de la U.S). Teniendo en cuenta estos elementos la restricción del presupuesto asignado es:
Función objetivo
La función objetivo informa acerca de la meta que se quiere alcanzar con la solución del problema. En este caso, como el interés del estudio consiste en ralear la mayor cantidad de rodales posibles, de acuerdo con la asignación de recursos de la Unidad Silvícola, la función objetivo representa la sumatoria de los rodales; esto es, la totalidad de rodales a ralear y se plantea:
De este modo, el problema que se presenta en la Unidad Silvícola queda planteado en el modelo de la siguiente forma: Modelación del raleo en plantaciones de Pinus caribaea var. caribaea de la Unidad Silvícola San Juan y Martínez:
Solución del modelo obtenido
Para la solución del modelo matemático obtenido se utiliza el software WINQSB, dentro de este, la opción "Linear and Interger Programming". Este emplea un procedimiento iterativo nombrado Método Símplex, que va buscando soluciones factibles hasta llegar a la soluciòn básica óptima.
Resultados
Evaluación de la actividad de raleo en relación con la Norma Ramal 595.
Solución del Modelo de Programación Lineal para la optimización del raleo en plantaciones de Pinus caribaea.
El modelo obtenido se solucionó mediante el módulo "Linear and Interger Programming" del software WinQSB (Chang, 2003). Se tuvieron en cuenta los 80 rodales con sus respectivos tipos de raleo planificados, el combustible y el presupuesto asignados. Además, se tuvo en cuenta la calidad de sitio, de modo que se resolvieron diferentes problemas, en dependencia del tipo de raleo planificado y la calidad de sitio del rodal.
Análisis de la solución
En el análisis se presenta la solución que considera el orden establecido según el tipo de raleo y la calidad de sitio, de modo que el modelo respete que primero se deben ralear aquellos rodales a los que les corresponde el raleo I y que se encuentren en áreas con calidad de sitio II.
Planificación del raleo I.
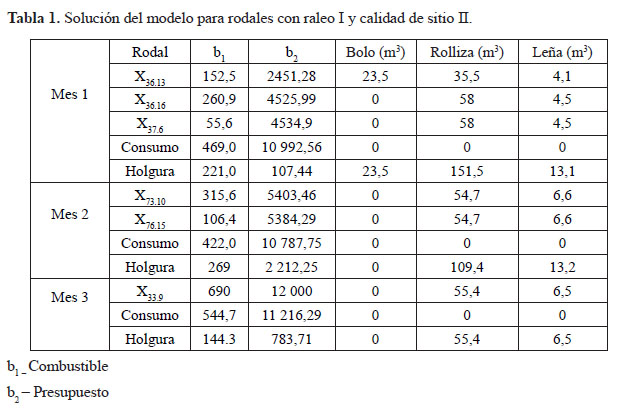
Las tablas 1 muestra la solución del modelo para rodales con raleo I ubicados en áreas con calidad de sitio II.
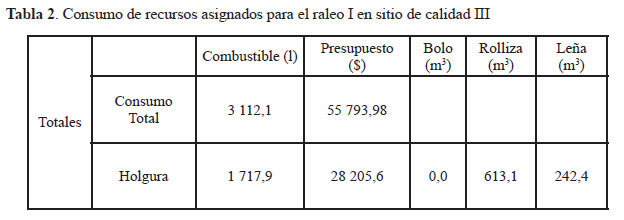
La tabla 2 muestra el consumo de los recursos asignados para el raleo I en plantaciones ubicadas en sitios de calidad III.
El rodal (X 66.14) es el único con raleo I recomendado en áreas con calidad de sitio IV, la ejecución del tratamiento puede ejecutarse en un mes con una única asignación de recursos. Esto implica un consumo de 684 litros de combustible y un costo total de $ 9 345,53. Este raleo aporta un total de14, 5 m3 de madera rolliza y 24,4 m3 de leña.
Planificación del raleo II
Existen solamente dos rodales con raleo II ubicados en sitio de calidad de sitio II. El consumo total de recursos de ambos puede asumirse con una única asignación de la empresa, por lo que es posible ralear ambos en el mismo mes, implicando un consumo de 36,20 litros y un costo total de $ 8 347,77. Este raleo permitirá obtener un total de 27,1 m3 de madera en bolo 68,4 m3 de madera rolliza y 4,2 m3 de leña.
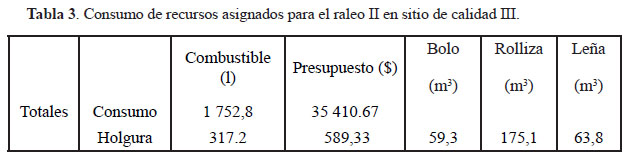
Los totales de consumo de los recursos asignados para el raleo II en rodales ubicados en sitios con calidad de sitio III se muestran en la tabla 3.
La planificación del raleo II en rodales ubicados en sitio con calidad III se puede realizar en un total de tres meses apreciándose que el primer mes es más efectivo pues al realizarse la actividad se consumen un total de 11,90 litros de combustible y $ 9 715.25 lo que contribuye a un ahorro 78 litros y $ 284,75. La tabla 4 muestra que le entidad ahorra un total de 317.2 litros de combustible y $ 589,33. Esta combinación permite aprovechar 59.3 m3 de madera en bolo, 175.1 m3 de madera rolliza y 63,8m3 de leña.
Los cuatro rodales ubicados en sitios con calidad IV con raleo II recomendado para el período de estudio se pueden ralear en un mes con un consumo de 405.7 litros y $10 324.4.
Planificación del raleo III.
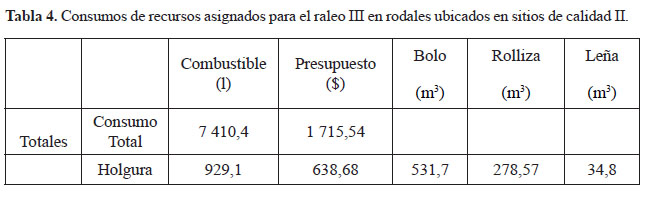
El consumo de recursos asignados para el raleo III en sitio de calidad II se muestran en la tabla 4.
El raleo III en los rodales ubicados en sitio de calidad II se planifica para seis meses, siendo el mes dos el de mayor efectividad. Se planifica la actividad a los rodales con un consumo total de 7 410,4 litros de combustible con una holgura de 929,1 litros y $1 715,54, ahorrando un total de $ 638,68 a la entidad.
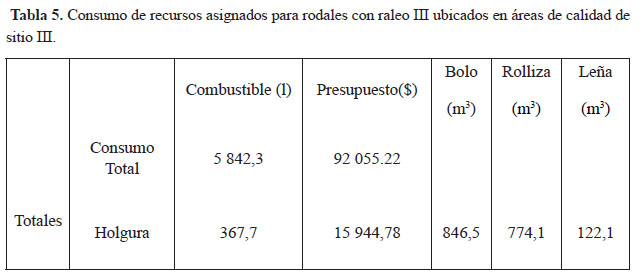
La tabla 5 muestra el consumo de recursos asignados para el raleo III en las plantaciones ubicadas en sitio de calidad II.
El raleo III en los rodales ubicados en sitio de calidad III se planifica para nueve meses, siendo el mes dos el de mayor efectividad. De los 6 210 litros de combustible y $108 000 asignados para el periodo se consume un total de 5 842,3 l y $ 92 055,22 con una holgura de 367,7 litros y $ 15 944,78 lo que constituye un ahorro significativo para la entidad.
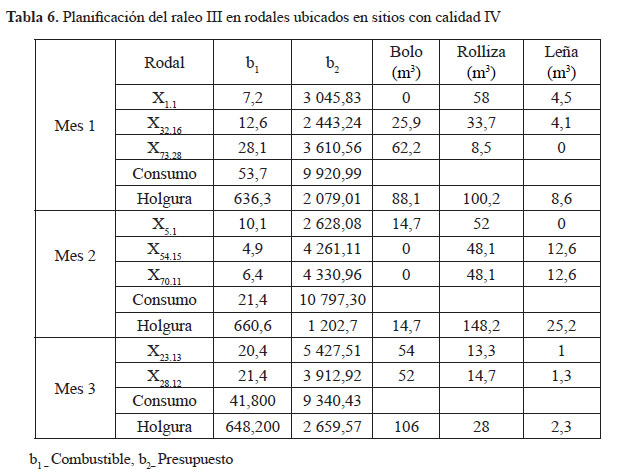
Se muestra la planificación del raleo III en rodales ubicados en sitios con calidad IV (Tabla 6).
Los resultados muestran que el raleo III se puede realizar en un total de tres meses, siendo el mes uno el más efectivo pues la actividad consume un total de 573,7 litros de combustible y $ 9 920,9 con un ahorro para la Unidad Silvícola de 636,3 litros de combustible y $2 079,01.
Al analizar la solución del modelo para todos los rodales (873 ha) con raleos propuestos para el decenio 2006-2016 se constata que la actividad se puede realizar en un total de 30 meses.
De acuerdo con la disponibilidad de presupuesto y el gasto asociado al raleo de cada rodal, como máximo, en un mes se podrán ralear seis rodales, es decir, es posible ralear los cinco rodales que tienen asociado un menor costo y cualquier otro cuyo costo sea menor de $3 757,25.
Al realizar una comparación entre los resultados obtenidos del modelo y la planificación de la Unidad Silvícola durante los 30 meses, se aprecia que la implementación del modelo ahorraría a la entidad un total de 1 726 litros de combustible y $ 1 291,26.
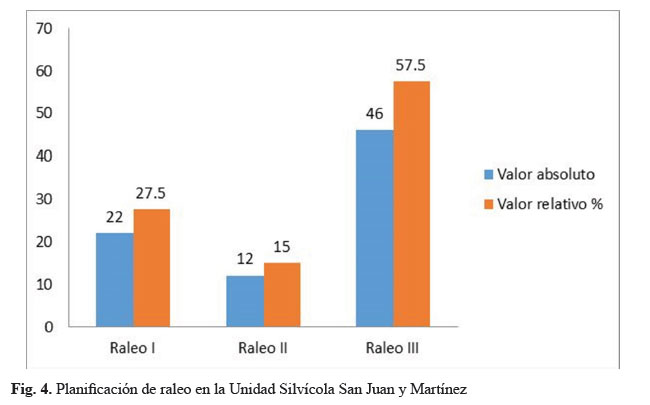
Con relación a los diferentes tipos de raleo se puede constatar que de los 80 rodales planificados según el Proyecto de Ordenación 46 (57,5 %) rodales tienen planificados raleo III, 12 (15 %) raleo II y 22 (27,5 %) raleo I (fig. 4).
Consideraciones adicionales
El orden del raleo se va conformando sobre la base de los rodales asociados a las variables que van resultando unitarias. Cada mes selecciona un grupo de rodales (los que toman valor 1). Estos se extraen para resolver el modelo en el mes siguiente, donde se asignan las mismas cantidades de combustible y presupuesto, según lo dispuesto por la Unidad Silvícola.
Los análisis concluyen cuando han sido analizadas todas las áreas o cuando se han agotado los recursos disponibles.
Significación económica
A la hora de planificar los raleos en una entidad forestal es imposible no tener en consideración el aspecto económico, en este sentido en la presente investigación se realizó una planificación de los rodales a ralear optimizando los recursos materiales y financieros (combustible y presupuesto) asignados a la Unidad Silvícola.
Para este fin se seleccionaron los 80 rodales con raleos recomendados en el proyecto de Ordenación vigente en el período 2006 – 2016 y se solucionó el modelo de Programación Lineal.
En el Proyecto de Ordenación, el raleo se planifica para un total de 10 años con una asignación de 82 800 litros de combustible y $ 1 440 000,00 cifra que debe variar al incorporarse cada año nuevas áreas a clases de desarrollo superiores. Los resultados obtenidos de la solución del problema informan que los 80 rodales seleccionados se pueden ralear en un período de 30 meses (dos años y seis meses).
Si se consideran los aspectos establecidos en la Norma Ramal 595 para la actividad, referida al calendario de ejecución de diciembre a marzo (4 meses), y a la superficie establecida para ralear, este resultado equivaldría a siete años y seis meses.
Para el total de meses dedicados a la actividad, la asignación de presupuesto y combustible es de $1 440 000,00 y 82 800 litros respectivamente. Considerando los resultados del modelo, la actividad se realizaría en dos años y seis meses, con un consumo total de 973,2 litros de combustible y $ 298 708,74 de presupuesto, lo que representa, en ambos recursos, un ahorro de 19 726,8 litros y $ 61 291, 26 para la Unidad Silvícola. Ello demuestra la factibilidad económica obtenida con el procedimiento realizado.
Considerando este resultado, el modelo elaborado constituye una herramienta eficaz para planificar la actividad de raleo con un uso óptimo de los recursos, teniendo en cuenta las condiciones tecnológicas de la entidad.
Discusión
Evaluación de la actividad de raleo en relación con la Norma Ramal 595.
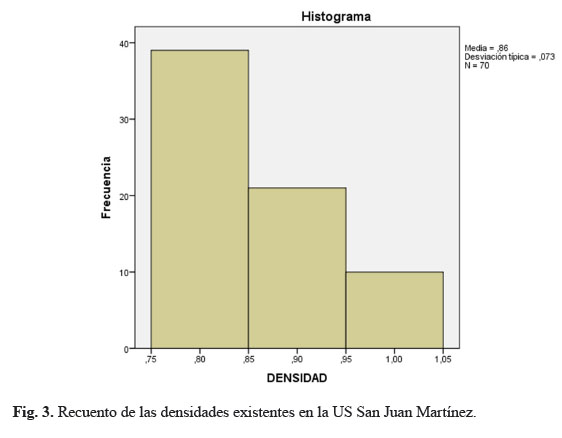
La frecuencia de la densidad refiere que el mayor número de los rodales tienen densidades de 0,8 y 0,9 (Figura 3) lo que demuestra la incidencia del raleo en la obtención de bajos rendimientos de madera en bolo, en las plantaciones destinadas a producir madera para aserrío.
Al respecto Castillo y Aguirre (2017) determinaron una función de probabilidad de densidad que permite la estimación del número de árboles por clase diamétricas en plantaciones de P. caribaea como herramienta para la toma de decisiones sobre la actividad de raleo en dichas plantaciones. Además la necesidad de raleo en las plantaciones, teniendo en cuenta que un número mayor de árboles del adecuado en un área reduciría el rendimiento por árbol y un número menor de árboles sub-utilizaría el sitio (Robles, 2007).
Valdés (2011) refiere que en los bosques jóvenes donde se aplica el raleo I para la formación de la composición, su realización es independiente de la posibilidad de la venta de la madera que se extraiga. En los bosques de edades superiores donde se aplica el raleo II y III se tiene en cuenta la venta de la madera talada considerando la economía de la actividad forestal.
Sin embargo West (2006) asevera que el raleo y la poda son las prácticas silviculturales que condicionan en gran medida la calidad y cantidad de productos con destino a aserrado. El objetivo consiste en disminuir la competencia intraespecífica para maximizar el crecimiento de los mejores árboles del rodal, de forma tal que se puedan obtener árboles de mayor tamaño en menos tiempo del que se obtendrían de una plantación no raleada.
Estos resultados también reafirman lo planteado por Barrero (2010) referido a que la calidad de sitio es uno de los factores más importantes que determinan el crecimiento de los árboles y de las masas forestales, así como la producción de los terrenos. El índice de sitio es una representación gráfica que describe la relación altura dominante-edad de un rodal o árboles individuales y define el grado de productividad de un lugar.
Solución del Modelo de Programación Lineal para la optimización del raleo en plantaciones de Pinus caribaea
Los modelos económico matemáticos se utilizan frecuentemente para la fundamentación y toma de decisiones económicas (Domínguez, 2012).
Para los investigadores forestales, prestan su máxima utilidad al servir de herramientas para investigar acerca de la dinámica forestal (Abellanas et al. 2009).
Estos se utilizan como un instrumento común en el estudio de sistemas de diversas características (Torres et al. 2009), por lo que están considerados como un elemento indispensable en la investigación científica (Davison, 2008).
Al igual que en otras ramas del saber, en las ciencias forestales se ha hecho necesario el estudio de los fenómenos del mundo real a través de la modelación matemática de tal manera que, el crecimiento y la producción de una plantación forestal coetánea son variables predecibles a través de modelos matemáticos, entre los que se encuentran los propuestos por Prodan et al. (1997), Crechi et al. (1999, 2000), Sanquetta (2001) García (2004), Barrero (2010), Chikumbo y Nicholas (2011), Bravo et al. (2011, 2012), Bergseng et al. (2012), así como (Gharis et al. 2014). Asimismo, el uso de modelos de optimización en este ámbito ha sido ampliamente estudiado en las últimas décadas destacando principalmente los modelos lineales (Rönnqvist, 2003).
Diferentes autores coinciden en la utilidad de la Programación lineal en la solución de problemas para el desarrollo de la actividad forestal entre ellos: Fosado (1997) utilizó modelos de Programación Lineal tomando como restricciones los planes de producción, la disponibilidad de tiempo, disponibilidad de materia prima y restricciones informativas.
Cándano (1998) utilizó los modelos matemáticos de Programación Lineal para estimar el tiempo de las operaciones de aprovechamiento de madera (tiempo de tala, desrame y troceado de árboles), también utilizó esos tipos de modelos para predecir el tiempo de ciclo de extracción de maderas con tractores y con animales, así como modelos matemáticos para determinar el tiempo estimado en el transporte de madera en la provincia de Pinar del Río. León (1999) utiliza la Programación Lineal en el perfeccionamiento de la ordenación de las plantaciones puras.
León et al. (2008) realizaron un análisis de la evolución de un modelo de programación por metas en el contexto forestal cubano. Pimentel et al. (2010) emplearon la programación para la Modelación matemática contribuyendo a planificar el turno de corta de Pinus caribaea Morelet var. caribaea. Cándano et al. (2012) optimizaron el costo del sistema de aprovechamiento de madera en bosques naturales de Pinus caribaea en la provincia de Pinar del Río con el empleo de la programación lineal. Guera (2013) obtuvieron un modelo matemático de extracción-transporte de madera y control de calidad de madera aserrada para Pinus caribaea Morelet var. caribaea Barret y Golfari en la Empresa Agroforestal Macurije. Castillo et al. (2014, 2015) obtuvieron un modelo preliminar para la optimización del raleo en plantaciones de Pinus caribaea Morelet var. caribaea Barret y Golfari, mediante un modelo matemático. Van et al. (2014) desarrollaron un modelo de gestión estratégico para producción de carbón vegetal por programación lineal en la EFI Pinar del Río.
Conclusiones
El modelo matemático de programación lineal obtenido, planifica los rodales que deben recibir tratamiento silvicultural con las cantidades óptimas de combustible y presupuesto a emplear, la actividad se realiza en dos años y seis meses, con un consumo total de 973,2 litros de combustible y $ 298 708,74 de presupuesto.
El modelo ordena los rodales que debe recibir el tratamiento silvicultural, mostrando el tipo de raleo y el orden del mismo, de modo que se optimice la actividad, maximizando el número de rodales a ralear en la Unidad Silvícola San Juan y Martínez.
Contribución de Autores
BRC: Levanto los datos de campo, analizó la información, aplicó la modelación matemática y escribió el manuscrito. ZA: Reviso y realizó aportes a la versión final del articulo cinetífico.
Literatura citada
Abellanas, M.; B. Abellanas; O. García & C. Vilas. 2009. Vorest: Un modelo informático para simular el crecimiento de un bosque, Departamento de Matemática Aplicada de la Facultad de Informática de la Universidad Politécnica de Madrid y el Departamento de Ingeniería Forestal de la Universidad de Córdoba, Disponible en: http://supertoolbar,ask,com. [ Links ]
Aldana, E.; J. Rodríguez; G. Padilla & I. García. 2009. Análisis de diferentes edades para establecer el turno de tala en plantaciones de Pinus caribaea. Barrero, H. (2010). Modelo integral de crecimiento, perfil del fuste, grosor de corteza y estudio de la microdensidad de la madera para Pinus caribaea Morelet var, caribaea Barret y Golfari, Estudio de caso EFI Macurije, Tesis presentada en opción al Grado Científico de doctor en Ciencias Forestales Universidad de Pinar del Río. [ Links ]
Barrero, H. 2015. Curvas anamórficas de índice de sitio para plantaciones de Pinus caribaea Morelet var, caribaea Barret y Golfari de la Empresa Forestal Integral Macurije (EFI) en la provincia de Pinar del Río, Cuba, Revista Chapingo, Serie Ciencias Forestales y del Ambiente 17(2):245-252· August 2011 with 28 Reads DOI: 10,5154/r,rchscfa,2010,06,035. [ Links ]
Bergseng, E.; J. Andreas; E. Framstad; T. Gobakken; B. Solberg & H. Fredrik. 2012. Biodiversity protection and economics in long term boreal forest management A detailed case for the valuation of protection measures, Forest Policy and Economics 15 (2012) 12–21, Disponible en: www,elsevier,com/locate/forpol. [ Links ]
Bravo, J.; J. T. Suárez & J. M. Montalvo. 2012. Modelación matemática por hectárea de Pinus caribaea Morelet var, caribaea Barret y Golfari en la Empresa Forestal Integral La Palma, Revista Forestal Baracoa, 31 (1): 3-7. [ Links ]
Bravo, J.; W. Toirac & V. M. Fuentes. 2011. Modelación del crecimiento del diámetro medio de Pinus cubensis Griseb en la Empresa Forestal Integral Baracoa (Par te II), Revista Forestal Baracoa, 30 (2): 19 – 23. [ Links ]
Cándano, F. 1998. Propuesta para el perfeccionamiento de la tecnología de aprovechamiento de madera en rodales de Pinus caribaea en la Provincia de Pinar del Río, Tesis en opción al grado científico de Doctor en Ciencias Forestales, UPR, 117p. [ Links ]
Cándano, F.; A. M. Pinto & J. C. Martínez. 2012. Optimización del costo del sistema de aprovechamiento de madera en bosques naturales de Pinus caribaea, Revista CERNE vol,18 no,1 .
Castillo, B. R.; H. Barrero & V. P. Pérez. 2014. Optimización del raleo en plantaciones de Pinus caribaea Morelet var, caribaea Barret y Golfari mediante un modelo matemático, Revista Forestal Baracoa, Vol33, Número Especial, ISSN: 2078- 7235. [ Links ]
Castillo, B. R.; H. Barrero & V. P. Pérez. 2015: Tratamiento matemático para la selección del raleo en plantaciones de Pinus caribaea Morelet, Revista cubana de Ciencias Forestales CFORES ISSN-e-2310-3469, Vol, 3.
Castillo, B. & Z. Aguirre. 2017. Selección de funciones de densidad de probabilidad para plantaciones de Pinus caribaea var. caribaea (Pinaceae) en Pinar del Río (Cuba). Revista Arnaldoa 24 (1): 415-424, http://doi.org/10.22497/arnaldoa.232.23201. ISSN: 1815-8242 (edición impresa) ISSN: 2413-3299 (online edition). [ Links ]
Crechi, E.; H. Fassola & P. Ferrere. 1999. Proyecto Cooperativo Simuladores de Crecimiento, Pinus taeda. [ Links ]
Crechi, E.; H. Fassola; A. Friedl & R. Fernández. 2000. Efectos de la intensidad y oportunidad de raleo en Pinus taeda L, Sobre el crecimiento y la producción hasta los 11 años de edad en el Departamento Iguazú, Provincia de Misiones, Argentina. [ Links ]
Chikumbo, O. & I. Nicholas. 2011. Efficient thinning regimes for Eucalyptus fastigata: Multi-objective stand-level optimization using the island model genetic algorithm Ensis, Department of Forests, Scion, 49 Sala St, Private Bag 3020, Rotorua 3046, New Zealand, Ecological Modelling 2221683-1695, Elsevier. [ Links ]
Davison, A. C. 2008. Statistical models, Cambridge University Press, The Edinburgh Building, Cambridge CB2 8RU, UK, 726 p. [ Links ]
Domínguez, E, A. 2012. Fundamentos para la modelación matemática de sistemas complejos, [en línea] Disponible en: http://carusso,narod,ru/ nociones,doc [Consulta 6 de Agosto 2016] [ Links ].
Donoso, P.; I. Díaz; M. González & C. Salas. 2013. Silviculture to promote old-growth forest attributes effects of ecological thinnings on second -growth forest in south -central Chile, Informe de avance proyecto FONDECYT 1110744. [ Links ]
Felipe, P.; B. Rodríguez; N. Ruíz; A. González & P. Álvarez. 2001. Programación Matemática I, Editorial Félix Varela, Universidad de La Habana. [ Links ]
Fosado, O. 1999. Tratamiento económico matemático de la planificación operativa del proceso de aserrado de la madera, Tesis presentada en opción al grado científico de Doctor en Ciencias Forestales, Universidad de Pinar del Río, Pinar del Río, Cuba. [ Links ]
García, I. 2004. Bases para el control y planificación del Pinus caribaea Morelet var caribaea Barret y Golfari en la provincia de Pinar del Río, Tesis en opción al título de Máster en Ciencias Forestales, mención Manejo de Bosques, UPR Pinar del Río. [ Links ]
Gharis, L.; J. Roise & J. McCarter. 2014. A compromise-programming model for developing the cost of including carbon pools and flux into forest management, Department of Forestry and Environmental Resources, North Carolina State University, USA, Springer Science Business Media New York. [ Links ]
Goberna, M. 2006. Medio siglo de Programación Lineal, Universidad de Alicante, España. [ Links ]
Gra, A.; K. Lockow; A. Vidal; J. Rodríguez; M. Echeverría & C. Figuerroa. 1990. Tablas de Volumen y surtido y densidad del Pinus caribaea en plantaciones puras para Cuba, Informe etapa 509-09,24. [ Links ]
Guelmez, J. & M. Acosta. 2007. Proyecto de Ordenación EFI Pinar del Río.
Guera, M. 2013. Modelo matemático de extracción transporte de madera y control de calidad de madera aserrada para Pinus caribaea Morelet var, caribaea Barret y Golfari, Estudio de caso EFI Macurije,Tesis en opción al título de Máster en Ciencias Ambientales, Universidad de Pinar del Río, Cuba. [ Links ]
Herrero, J. 2015. Diálogo nacional sobre la implementación de un sistema de C&I para el Manejo Forestal Sostenible en Cuba, Taller Regional Latinoamericano sobre Criterios e Indicadores para el Manejo Forestal Sostenible, Tarapoto, Perú [ Links ].
León, M, A.; Hernández; T. Gómez; J. Guelmes; J. Molina & R. Caballero. 2008. Evolución de un modelo de programación por metas en el contexto forestal cubano, Revista investigación operacional, 2 (2):130-39.
León, M. A. 1999. Tratamiento económico - matemático en el perfeccionamiento de la Ordenación de plantaciones puras, Tesis presentada en opción al grado científico de Doctor en Ciencias Forestales, UPR, Pinar del Río, Cuba. [ Links ]
Ministerio de la Agricultura. 2006. Estrategia de Desarrollo Forestal 2005-2015, Cuba. [ Links ]
Norma Ramal. 595/1982. Tratamientos Silviculturales, DNMCC, Dirección de normalización, meteorología y Control de la Calidad, Ministerio de la Agricultura. [ Links ]
Ortiz, J. 2000. Modelación y simulación matemática del reciclaje de N, P y K en sistemas de pastoreo vacuno en Cuba. Tesis presentada en opción al título de Doctor en Ciencias Veterinarias. Instituto de Ciencia Animal. La Habana, Cuba. [ Links ]
Peraza, O. 2011. Turno financiero y técnico forestal para Pinus caribaea Morelet var, caribaea Barret y Golfari en sitios de la Provincia de Pinar del Río, Tesis en opción al título académico de Master en Ciencias Forestales. [ Links ]
Pimentel, K.; D. Costa & R. Pérez. 2010. Modelación matemática para planificar el turno de corta de Pinus caribaea Morelet var, caribaea, Revista Avances, Vol 13, No 2. [ Links ]
Prodan, M.; R. Peters; F. Cox & P. Real. 1997. Mensura Forestal, Serie Investigación y Educación en Desarrollo Sostenible, Proyecto IICA/GTZ sobre agricultura, recursos naturales y desarrollo sostenible, San José, Costa Rica. [ Links ]
Robles, J. 2007. Comparación de las cantidades ofertadas y demandadas de madera de diámetros menores (818 cm) procedente del primer raleo, en plantaciones del programa de incentivos forestales, en la región II del Instituto Nacional de Bosque Guatemala Universidad de San Carlos de Guatemala, Facultad de Agronomía. [ Links ]
Rönnqvist, M. 2003. Optimization in Forestry, Math, Program, 97: 267- 284. [ Links ]
Russo, I. 2015. Situación del sector Forestal en Cuba al cierre del 2014, Conferencia desarrollada en el II Taller Nacional de Silvicultura, Dirección National Forestal, Cienfuegos, Cuba. [ Links ]
Sanquetta, C, R.; L. Farinha; J. Eduard & A. Aparecida. 2001. Ecuaciones de biomasa aérea y subterránea en plantaciones de Pinus taeda en el sur del Estado de Paraná Brasil. [ Links ]
Servicio Estatal Forestal. 2014. Dinámica Forestal de la Empresa Agroforestal Pinar del Río, Cuba. [ Links ]
Torres, V. & J. Ortiz. 2005. Aplicaciones de la modelación y simulación en la producción y alimentación de animales de granja, Rev, Cubana Ciencias Agrícolas, 39: 397. [ Links ]
Torres, V.; I. Sampaio & O. Fundora. 2009. Modelo estocástico del comportamiento productivo en las etapas crecimiento de búfalos de agua en Cuba, Rev, Cubana Ciencias, Agrícolas, 43: 113. [ Links ]
Valdéz, D. 2011. Efectos de raleos aplicados durante el periodo 2005 a 2008 a una plantación de la especie palo blanco (Tabebuia donnellsmithii Rose) en finca Masaya, El Palmar, Quetzaltenango, Guatemala, Universidad Rafael Landivar. [ Links ]
Van, A.; M. García y Garofalo. 2014. Modelo de gestión estratégica para producción de carbón vegetal por programación lineal en la EFI Pinar del Río. Revista Avances 16(3): 213 - 220.
Recibido: 20-I-2018
Aceptado: 28-II-2018
Publicado online: 30-VII-2018
Publicado impreso: 30-VIII-2018