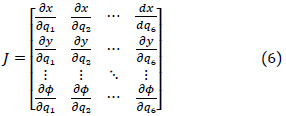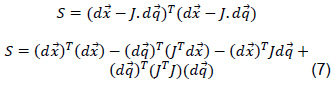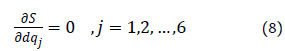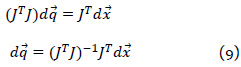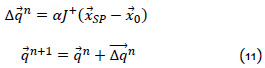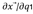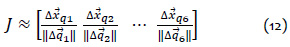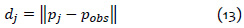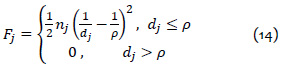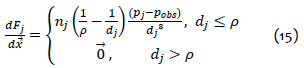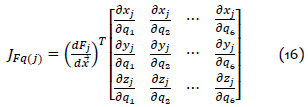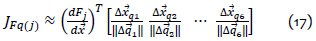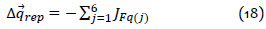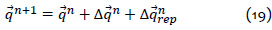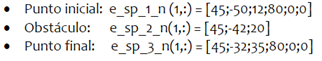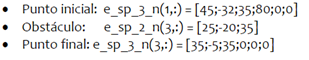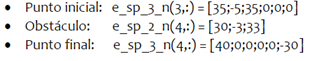INTRODUCCION
La planificación de movimiento consiste en encontrar una ruta libre de colisión desde una configuración inicial de posición y orientación hasta una configuración final [1].
Muchas de las tareas en robótica hoy en día requieren de una planificación del movimiento que se tiene que realizar antes de ejecutar dichos movimientos con el fin de hacer que estas tareas complejas se ejecuten de una forma segura y autónoma. Por eso, en el estado del arte se encuentra una gran cantidad de artículos relacionados a este tema.
Uno de los primeros trabajos iniciales de investigación acerca de algoritmos de evasión de obstáculos fue desarrollado por Johan Borenstein et al [2] en el cual usa campos potenciales y fusión de sensores para que un robot móvil recorra un trayecto y no se detenga abruptamente ante un obstáculo. Zemin Liu et al [3] desarrolla una variación del algoritmo de árboles aleatorios estrella usando campos potenciales artificiales con el fin de reducir el tiempo de ejecución del algoritmo y obtener un tiempo de ejecución menor.
En el caso de manipuladores antropomórficos que realizan tareas de “pick and place”, los objetos a manipular presentan diferentes ubicaciones iniciales y requieren ser colocados en distintas posiciones objetivo, debido a esta variabilidad en los procesos se requieren de algoritmos que puedan generar trayectorias de manera autónoma.
Existen métodos de planificación de movimiento que están basados en el concepto de espacio de configuraciones como son las técnicas de hoja de ruta [4] y los algoritmos de descomposición de celdas [5], que tradicionalmente se usan para resolver problemas de planificación en espacios de configuraciones de baja dimensionalidad siendo computacionalmente ineficiente para casos de alta dimensionalidad, como los manipuladores robóticos [6]. Otros métodos están basados en el espacio de trabajo que consisten en encontrar una ruta en el espacio geométrico euclidiano. Por ejemplo, el método de campos potenciales utiliza el espacio de trabajo donde modela campos potenciales artificiales debido a los polos de repulsión que son los obstáculos y un polo de atracción que es el punto objetivo, de esta manera se logra que el robot pueda moverse de una forma segura hasta su posición final [1].
El método de campos potenciales es ampliamente utilizado en el campo de navegación de robots móviles debido a su fácil implementación [7]. Sin embargo, también han sido implementados en simulación de manipuladores altamente redundantes [8], [9]. Asimismo, Rajendran [10] desarrolla un método de planificación de movimiento aplicado a manipuladores robóticos que se encuentran en espacios desorganizados y con muchos obstáculos. Su técnica se basa en aproximaciones locales de su espacio de configuraciones y también se basa en arboles de búsquedas.
En este trabajo de investigación, se presenta en primer lugar el modelamiento de la cinemática directa del modelo mecánico del manipulador de seis grados de libertad propuesto mediante el método Denavit-Hartenberg. Luego, se realiza la cinemática inversa del modelo mediante un método iterativo que optimiza una función de costo con el fin de tener una solución única; el cual es regulado mediante un hiperparámetro. Luego se realiza la cinemática inversa planificada mediante la adición de 6 fuerzas repulsivas a las seis juntas y se define su función de costo, así como su representación en la arquitectura general del algoritmo. Luego se genera empíricamente una base de datos de trayectorias optimizados en base a tres clases de pérdida. Finalmente se realiza las simulaciones usando la arquitectura construida y se presenta al final los resultados y conclusiones del trabajo de investigación.
METODOLOGÍA
Modelamiento Geométrico Directo
El modelo de Geometría Directa tiene como propósito generar una función capaz de calcular el vector de posición-orientación del efector final del robot en base a los valores de rotación de los 6 motores del robot. Como primer paso, necesitamos definir las relaciones matemáticas entre los diferentes vectores de posición correspondientes a las uniones del robot y la configuración correspondiente del robot mediante las matrices de Denavit-Hartenberg [11].
Podemos definir la función DH como la matriz Denavit-Hartenberg como:
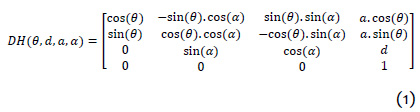
De esta forma, las matrices de transformación se definirán como:

Luego, la función que calcula la matriz de transformación del efector final a partir de los valores de rotación de los 6 motores se definirá como:

De esta matriz de transformación podemos obtener el vector de posición cartesiana y el vector de orientación (considerando las orientaciones de Yaw, Pitch y Roll) de la forma que se define en la ecuación (4).
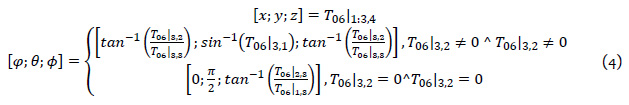
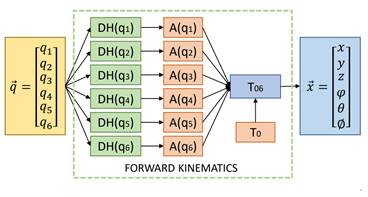
Finalmente, podemos definir el vector de posición del efector como el vector 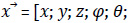 , que podría calcularse a partir de la matriz 𝑇06 y por lo tanto a partir de los 6 valores de rotación de los motores. La arquitectura de información del procesamiento de señales se muestra en la figura 1.
, que podría calcularse a partir de la matriz 𝑇06 y por lo tanto a partir de los 6 valores de rotación de los motores. La arquitectura de información del procesamiento de señales se muestra en la figura 1.
Modelamiento Geométrico Inverso
Se propone un método iterativo, que optimiza la ecuación diferencial que define la relación entre los vectores 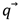 y
y 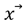 . Por esta razón, este método encuentra solo una solución que cambiaría según el valor del hiperparámetro “velocidad de optimización” seleccionado y la configuración inicial del robot. La ecuación diferencial se define en (5).
. Por esta razón, este método encuentra solo una solución que cambiaría según el valor del hiperparámetro “velocidad de optimización” seleccionado y la configuración inicial del robot. La ecuación diferencial se define en (5).
Donde J es la matriz jacobiana definida como:
Para optimizar esta ecuación diferencial, definimos la variable de pérdida S como:
Como en el modelo de geometría inversa se calcula iterativamente los valores necesarios de 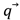 para alcanzar un
para alcanzar un 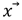 establecido, se minimiza el valor de S modificando los valores de
establecido, se minimiza el valor de S modificando los valores de 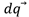 , por lo tanto, se define la optimización de la variable de pérdida S con respecto a la variable
, por lo tanto, se define la optimización de la variable de pérdida S con respecto a la variable 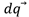 de acuerdo a la siguiente ecuación diferencial parcial:
de acuerdo a la siguiente ecuación diferencial parcial:
Luego tras reemplazar el valor de S en esta ecuación de optimización:
Donde a 𝐽+ = (𝐽𝑇𝐽)−1𝐽𝑇 se le denomina el pseudoinverso de la matriz jacobiana, porque transforma la primera ecuación diferencial en la siguiente ecuación diferencial:
Luego, para calcular los valores necesarios de 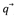 , se define el vector objetivo como
, se define el vector objetivo como 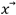 𝑆𝑃 y se realiza un proceso iterativo definido de la siguiente forma:
𝑆𝑃 y se realiza un proceso iterativo definido de la siguiente forma:
Donde 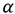 es el hiperparámetro del modelo de geometría inversa que establece la velocidad de la optimización.
es el hiperparámetro del modelo de geometría inversa que establece la velocidad de la optimización.
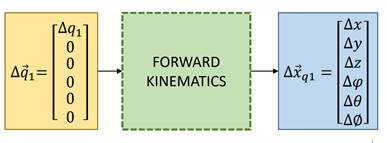
El único problema con este enfoque es el cálculo de la matriz jacobiana J, ya que requiere soluciones analíticas de todos los elementos de la matriz. Sin embargo, con el modelo de la geometría directa definido en el apartado anterior, se puede calcular indirectamente una aproximación de esta matriz. En la figura 2 se muestra cómo usar este modelo para calcular los valores aproximados de los valores diferenciales parciales del vector 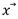 con respecto al valor diferencial del vector
con respecto al valor diferencial del vector 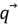 .
.
Por consiguiente, se calcula la matriz jacobiana aproximada repitiendo el proceso que se muestra en la figura 2 con las variaciones de todos los valores de rotación de los motores. Así, se obtiene:
Finalmente, podemos aplicar las ecuaciones iterativas definidas anteriormente para actualizar los valores del vector 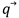 hasta que el sistema alcance el vector deseado
hasta que el sistema alcance el vector deseado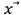 . La arquitectura de información del procesamiento de señales se muestra en la figura 3.
. La arquitectura de información del procesamiento de señales se muestra en la figura 3.
Modelamiento Geométrico Planificado
Ya que el enfoque elegido para el modelo de geometría inversa se basa en un proceso iterativo y se define como un bucle de control multivariable (figura 3), se puede modificar este modelo para permitir que el sistema encuentre un camino que evite tanto un obstáculo como un alcance el vector requerido 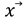 . Para este propósito, se utiliza como base el modelo de planificación de la trayectoria de campos potenciales para desarrollar un modelo de Geometría Inversa Planificada.
. Para este propósito, se utiliza como base el modelo de planificación de la trayectoria de campos potenciales para desarrollar un modelo de Geometría Inversa Planificada.
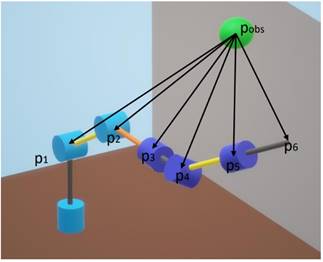
Se definen 6 fuerzas de repulsión de las 6 distancias mostradas en la figura 4. Cada una de estas distancias considera un punto correspondiente al extremo de una de las articulaciones del robot y el punto de la posición del obstáculo ().
Luego, se define la fuerza repulsiva de cada distancia como:
En consecuencia, la derivada parcial de la fuerza de repulsión respecto de las coordenadas xyz (sin considerar las orientaciones) es:
Asimismo, se define las matrices parciales Jacobianas para los 6 diferentes puntos del robot como:
Para calcular estas matrices Jacobianas parciales, se procede a calcular de una manera similar al método para calcular la matriz del Jacobiano para el modelo de geometría inversa, que se describió anteriormente. Entonces se tiene:
De acuerdo con la definición de fuerzas repulsivas se tiene la siguiente ecuación:
Donde el vector 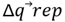 define los valores necesarios para cambiar en los valores de rotación de 6 motores para que la posición actual del robot no choque con el obstáculo.
define los valores necesarios para cambiar en los valores de rotación de 6 motores para que la posición actual del robot no choque con el obstáculo.
Finalmente, hemos definido como modelo de atracción el modelo de geometría inversa. Por lo tanto, el proceso iterativo será definido por la regla:
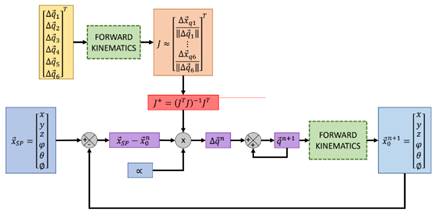
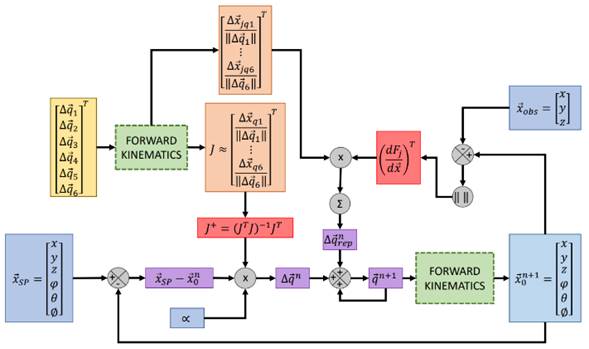
Luego, la arquitectura de información del procesamiento de señales se muestra en la figura 5. Se puede observar el sistema de control del robot y una compensación debido a la evasión de obstáculo requerida.
Generación de la Red Neuronal Supervisada
Para realizar el entrenamiento de la red neuronal supervisada se generó una base de datos con trayectorias optimizadas empíricamente en base a tres clases de pérdidas: pérdidas por energía potencial, pérdidas por precisión de posicionamiento y pérdidas por el campo de repulsión.
Con el modelo de geometría inversa planificada por campos potenciales se generaron 2000 trayectorias con los mismos vectores de posicionamiento (posiciones y orientaciones inicial y final) y posición del obstáculo en los cuales se varió los hiperparámetros de velocidad de movimiento y los coeficientes de campos vectoriales. Luego se realizó la simulación y se obtuvieron sus respectivos valores de pérdidas. Después se seleccionó solo una trayectoria con la menor pérdida relativa respecto a las otras, considerándose esta la trayectoria con parámetros optimizados.
La base de datos se generó repitiendo el proceso anterior, debido a la gran carga computacional para generar dicha base de datos, se ejecutaron las simulaciones en paralelo en 4 computadoras del Centro de Cálculo de UNIFIM (Instituto de investigación de la Universidad Nacional de Ingeniería, Perú).
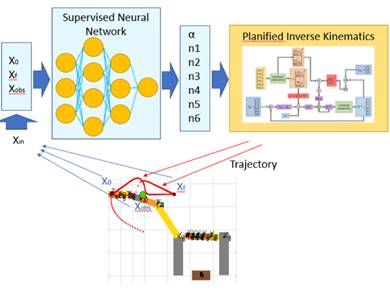
Con la base de datos generada, se desarrolló la programación del modelo de Red Neuronal Supervisada. Teniendo como datos de entrada los vectores de posicionamiento (X0, Xf y Xobs) y un conjunto de variables de salida (alpha, n1, n2, n3, n4, n5, n6) se prepararon los datos en Python con la librería pandas. Luego, empleando la librería de sckit-learn [12], sklearn se definió la red neuronal supervisada. Los hiperparámetros empleados fueron los que se muestran a continuación en la definición del modelo:

El proceso de la generación de trayectorias con la aplicación de la red neuronal se visualiza en el siguiente diagrama (figura 6). Donde, para realizar una trayectoria, inicialmente se introducen los vectores de posicionamiento y la posición del obstáculo, luego la red neuronal calcula los parámetros óptimos para dicha trayectoria que son ingresados al modelo de geometría inversa para ejecutar el movimiento en simulación.
SIMULACION Y RESULTADOS
Aplicación de la Red Neuronal Supervisada
Se realizó el entrenamiento de la red neuronal. Los resultados se muestran en la tabla I, donde se observa que la variable R2 correspondiente a la correlación entre las variables tiene un valor de 0.8184 aproximadamente.
TABLA I Resultados tras el entrenamiento de la Red Neuronal Supervisada.
| R2 score | 0.8184 |
| Función de costo | 21.7614 |
Por otro lado, la importancia que tiene cada variable en el poder de predicción de este modelo se muestra en la siguiente lista de “features importance” (tabla II) elaborada con un modelo de random forest auxiliar, de forma que se pueda obtener un peso por cada variable de entrada.
TABLA II “Features importance” del conjunto de datos empleado en el entrenamiento.
| Name | Score |
| X0(1) | 0.229275 |
| X0(3) | 0.228698 |
| X0(2) | 0.14784 |
| Xf(3) | 0.0656432 |
| Xf(2) | 0.0635456 |
| Xobs(3) | 0.0626281 |
| Xobs(2) | 0.0583687 |
| Xf(1) | 0.038695 |
| Xobs(1) | 0.0347584 |
| Xf(4) | 0.0244464 |
| X0(4) | 0.0227653 |
| Xf(6) | 0.0130426 |
| X0(6) | 0.0102939 |
| X0(5) | 0 |
| Xf(5) | 0 |
En cuanto a la aplicación para la selección de los hiperparámetros optimizados se ingresaron los siguientes vectores de posicionamiento para cuatro trayectorias de prueba:
Siendo los resultados obtenidos por el modelo de red neuronal supervisada entrenada con la base de datos acumulada los siguientes:
Con estos valores de parámetros obtenidos se presentan básicamente 2 errores, en la selección de los parámetros en la trayectoria 2 y la trayectoria 3. Esto se puede observar rápidamente en el primer parámetro generado por la red neuronal supervisada para estos movimientos, siendo en ambos casos negativos, lo cual contradice el requerimiento de posicionamiento que se le efectúa al modelo, pues al tener este parámetro un valor negativo, la dirección que originará será en sentido contrario al acercamiento a la posición solicitada. Además, estos parámetros negativos tienen un módulo bastante elevado, pues empíricamente se han observado valores de operación para el módulo de este parámetro del orden de 10-1, es decir valores entre 0.1 y 0.9 aproximadamente.
Aplicación del modelo de Geometría Inversa Planificada
Para la aplicación del modelo de geometría inversa planificada se implementaron dos manipuladores robóticos desacoplados, llamados robot1 y robot2, en el entorno Simulink-Matlab. El diagrama de bloques desarrollado recibe un vector de entrada de 12 elementos, de forma que contenga un vector de 6 elementos con las posiciones angulares del primer robot y un vector de 6 elementos con las posiciones angulares del segundo robot. En el modelo de bloques, los demultiplexores se encargan de separar los valores de los vectores para controlar el movimiento de las diferentes juntas de los robots.
De la sección anterior (redes neuronales), se pudo apreciar que el modelo de redes neuronales supervisadas no presenta un buen desempeño en predecir los mejores valores de hiperparámetros. Por ello, en esta sección se definen 4 vectores de posicionamiento con los hiperparámetros definidos por el programador. Además, se muestran los resultados obtenidos del modelo de geometría inversa planificada (figura 7) y de la simulación gráfica en Simulink con buenos resultados (figura 8).
Primera trayectoria: Requerimiento a robot 1
Segunda trayectoria: Requerimiento a robot 1
Tercera trayectoria: Requerimiento a robot 1
Cuarta trayectoria: Requerimiento a robot 2
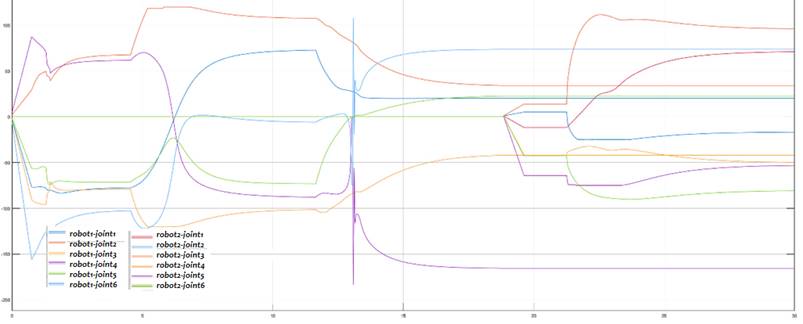
Fig. 7 Serie temporal de las posiciones angulares de ambos robots simulados bajo las trayectorias propuestas.
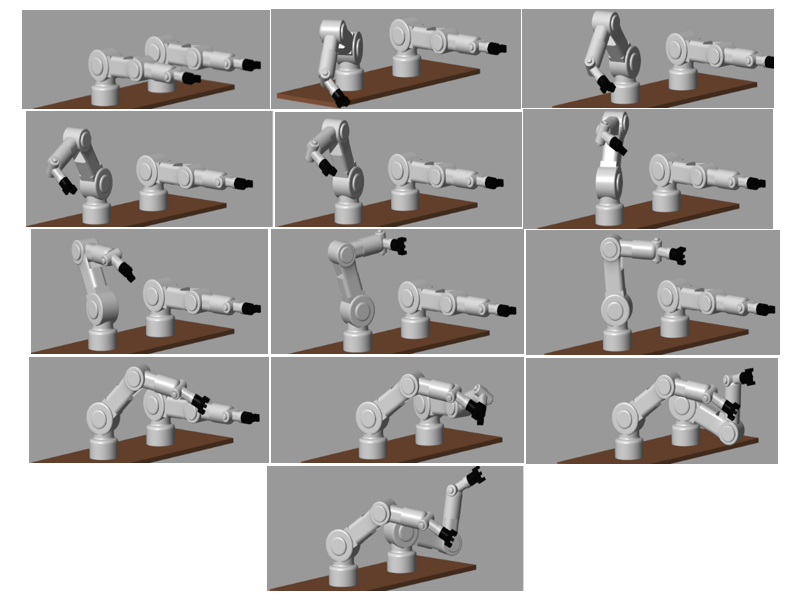
Fig. 8 Secuencia de movimientos de los robots 1 y 2 al simular el modelo de bloques de Simulink bajo las trayectorias propuestas.
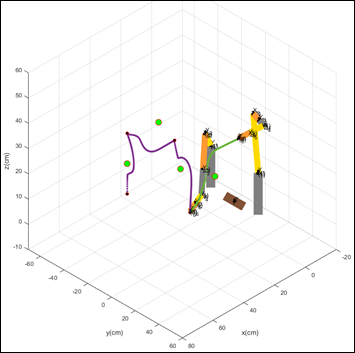
Los resultados del script desarrollado en Matlab se muestran en la figura 9, donde la trayectoria morada es ejecutada por el robot 1 y la verde por el robot 2.
DISCUSIÓN
De acuerdo con los resultados obtenidos, se puede ver que el manipulador robótico puede realizar la tarea de llegar al punto sin chocar los obstáculos usando el algoritmo propuesto. Sin embrago, el proceso para diseñar el algoritmo, así como la generación de trayectorias para la base de datos es tedioso. Por consiguiente, el método no es favorable cuando se tiene que hacer un prototipado rápido. Por el contrario, el algoritmo propuesto es una solución alternativa a los métodos clásicos y además se puede encontrar algunas mejoras al algoritmo propuesto con el fin de mejorar su rendimiento y hacerlo una opción más favorable a la hora de abordar el problema de planificación de movimiento aplicado en manipuladores robóticos.
CONCLUSIONES
La inclusión de un modelo de fuerzas vectoriales en un sistema de optimización de geometría inversa para un robot de 6GDL y una correcta selección de los hiperparámetros conducen a un modelo de geometría inversa planificada que permite al robot seguir una trayectoria entre dos posiciones requeridas mientras evita un obstáculo cuya ubicación es informada al robot. Es decir, se concluye que la consideración de los jacobianos de las variaciones de los ángulos de un robot de 6GDL con respecto a las fuerzas repulsivas de un modelo de campos vectoriales en un modelo que considera los jacobianos de las variaciones los ángulos del mismo robot con respecto a la distancia vectorial entre la posición actual y la posición final ha permitido generar un modelo de planificación de trayectorias con una base informada.
De acuerdo a los resultados empíricos se puede observar que empleando datos de trayectorias óptimas dentro de una región con valores de posiciones similares (tipo de trayectorias homogéneas) para el entrenamiento del modelo de red neuronal empleado se pueden obtener un buen desempeño de predicción, es decir el modelo permite que el robot genere trayectorias óptimas. Esto plantea la existencia de diferentes secciones del espacio que se caracterizan por diferentes predisposiciones en los valores de los modelos. Se concluye que se requiere un análisis más profundo del comportamiento de estos modelos sectorizados, pudiendo plantearse una nueva arquitectura de procesamiento de datos con el uso de clusterización para caracterizar los vectores de posicionamiento en diferentes tipos y realizar diferentes modelos para cada tipo, de forma que se obtenga un mejor desempeño, logrando el objetivo final de generación de trayectorias óptimas para cualquier conjunto de puntos de posicionamiento requerido y obstáculos.