Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO  uBio
uBio
Compartir
Revista de Investigaciones Veterinarias del Perú
versión impresa ISSN 1609-9117
Rev. investig. vet. Perú vol.24 no.3 Lima ago. 2013
Desarrollo y validación de un modelo de predicción del requerimiento óptimo de aminoácidos esenciales y del comportamiento productivo en ponedoras comerciales
Development and validation of a model to predict the optimum requirement of essential amino acids and performance in commercial laying hens
Elías Salvador1,3, Víctor Guevara2
1 Departamento de Producción Animal, Facultad de Medicina Veterinaria y Zootecnia, Universidad Nacional San Luis Gonzaga, Ica, Perú
2 Departamento de Nutrición, Facultad de Zootecnia, Universidad Nacional Agraria La Molina, Lima, Perú
3 E-mail:pronutri@hotmail.com, eliasnutri@yahoo.com. Web blog: http://eliasnutri.wordpress.com/
RESUMEN
Los objetivos del estudio fueron desarrollar y validar un modelo para predecir el requerimiento óptimo de aminoácidos esenciales y comportamiento productivo de gallinas de postura, en términos de proteína ideal (PI) y proteína balanceada (PB). Se calculó el consumo de alimento con una ecuación factorial desarrollada a partir de la teoría y el requerimiento de PI en base al promedio ponderado de los aminoácidos como porcentaje de la proteína de mantenimiento, ganancia de peso y del huevo. En base a la relación aminoácido depositado/aminoácido consumido que generó el nivel de los aminoácidos azufrados en la dieta, se establecieron cuatro niveles de PB (90, 100, 110 y 120%) en las dietas. Se distribuyeron 192 gallinas de postura en cuatro tratamientos dietarios en un diseño de bloques completamente al azar con cuatro repeticiones de 12 aves cada uno. La producción de huevos, consumo de alimento, conversión alimenticia, peso y masa de huevo fueron influenciados significativamente por el nivel de PB de la dieta, obteniéndose la mejor performance con el nivel de 110%. Al análisis de regresión, el requerimiento de PB para el máximo biológico fue de 109.4% y para el óptimo económico de la masa de huevo de 104%. En base a la literatura se generaron dos ecuaciones para predecir la masa de huevo y consumo de alimento, cuyos valores predichos y los observados en el presente experimento fueron sometidos al proceso de validación del modelo. Se encontró un error del modelo de 4.71% para la masa de huevo y de 2.44% para el consumo de alimento, lo que indica que el modelo de simulación del efecto de la PB sobre el rendimiento productivo es adecuado y puede ser útil para estimar el requerimiento óptimo de aminoácidos esenciales.
Palabras clave: modelo, requerimiento, predicción, proteína ideal, proteína balanceada, ponedoras, masa de huevo
ABSTRACT
The aims of the study were to develop and evaluate a model for predicting the optimum requirements of essential amino acids and performance in laying hens in terms of ideal and balanced protein. Feed consumption was estimated using a factorial equation developed from theory and the ideal protein requirement was calculated from the weighted average of amino acids as a percentage of the protein for maintenance, body weight gain, and egg production. The level of the sulfur amino acids of the diet was generated from the ratio deposited amino acids/consumed amino acids, from which four balanced protein levels (90, 100, 110, and 120%) in the diets were proposed. A total of 192 laying hens were randomly distributed to four dietary treatments in a completely randomized block design with four replicates containing 12 birds each. The results show that egg production, feed consumption, feed conversion, weight, and egg mass were significantly influenced by the level of balanced protein in the diet and the best performance was obtained with the level of 110%. Regression analysis revealed that the requirement of balanced protein for the biological maximum was 109.4% and for the economic optimum of egg mass was 104%. Two equations to predict egg mass and feed consumption were generated from the literature. Predicted values were evaluated against those observed in the present experiment. The error of model was of 4.71% for egg mass and 2.44% for feed consumption, which indicate that the simulation model of the effect of balanced protein on performance is adequate and can be useful to estimate the optimum requirement of essential amino acids.
Key words: model, requirement, prediction, ideal protein, balanced protein, laying hens, egg mass
INTRODUCCIÓN
Los requerimientos de aminoácidos en gallinas de postura comercial han sido tradicionalmente determinados por el método dosis- respuesta, evaluando la respuesta productiva del ave a determinados niveles de ingestión de un nutriente y manteniendo los otros constantes, teniendo como objetivo una respuesta máxima (máximo biológico). Sin embargo, los requerimientos nutricionales varían por factores como tamaño corporal, consumo de alimento, y producción y peso de huevos. Estos determinantes presentan cantidades medibles, de allí que es posible construir una ecuación para calcular el requerimiento (Hurwitz y Bornstein, 1973).
Se han desarrollado modelos con un enfoque factorial para la predicción del consumo de aminoácidos diarios para gallinas ponedoras (Filev et al., 1990), como los modelos Israelí y Reading desarrollados por Hurwitz y Bornstein (1973) y Fisher et al. (1973), respectivamente, que toman en cuenta las necesidades de composición del huevo, ganancia de peso y mantenimiento (Campos et al., 2008).
El método factorial constituye la base para la estimación de las necesidades que desarrollan los distintos modelos matemáticos. Dentro de este enfoque, el consumo de los aminoácidos estaría dado por la sumatoria de las necesidades de mantenimiento, crecimiento, deposición de proteína en el huevo y la eficacia con la que el aminoácido es utilizado. Sin embargo, se requiere estimar un gran número de parámetros cuyos valores son bastante imprecisos (Santomá, 1991).
Los modelos matemáticos integran ecuaciones de fenómenos biológicos como crecimiento, producción de huevos, incubación, digestión y absorción de nutrientes, utilizando variables cuantitativas para representar los factores que influencian el fenómeno (Rondón et al., 2002). El desarrollo de estos modelos requiere una etapa de diseño y ajuste y una de validación (Londoño et al., 2002). La evaluación del crecimiento animal y requerimientos de nutrientes ayudados por modelos matemáticos se ha convertido en un campo dinámico de desarrollo de investigación en nutrición (Halas y Babinsky, 2000).
La Proteína Ideal (PI), definida como el balance exacto de los aminoácidos, tiene por objetivo satisfacer los requisitos absolutos de todos los aminoácidos para mantenimiento y ganancia máxima de proteína corporal, reduciendo su uso como fuente de energía (Campos et al., 2008). En el caso de gallinas ponedoras sería satisfacer los requerimientos absolutos de aminoácidos para la producción de huevos. Su aplicación implica la reducción del nivel proteico y adición de aminoácidos sintéticos en la formulación de la dieta para disminuir los costos de producción (Campos et al., 2008) y maximizar el aprovechamiento proteico. En este contexto, es más importante el balance de aminoácidos en la dieta que los requerimientos de aminoácidos individuales.
En gallinas ponedoras, la metionina es el primer aminoácido limitante, seguido de la lisina en dietas maíz-soya (Schutte y De Jong, 1998), teniendo gran influencia sobre el tamaño de huevo y la producción. Asimismo, es importante fijar el requerimiento de metionina y cistina en la dieta (Joly, 2008). El perfil ideal de aminoácidos para gallinas ponedoras no está tan desarrollado como en pollos parrilleros y cerdos; sin embargo, el uso del perfil de PI para determinar el contenido de aminoácidos dietario tiene ventajas sobre los requerimientos de aminoácidos determinados empíricamente (Bregendahl y Roberts, 2009).
En el contexto de la formulación comercial, un perfil de PI exacto es teórico, por lo que se ha desarrollado el concepto de Proteína Balanceada (PB) como una aplicación práctica del perfil de aminoácidos ideal para abastecer a los pollos con los niveles mínimos correctos de aminoácidos esenciales y no esenciales (ROSS Nutrition Supplement, 2009). El desempeño de las aves puede ser mejorado con un incremento de los niveles de PB, pero hay factores nutricionales y medioambientales relacionados a la salud o de manejo, así como la forma y calidad del alimento, y tamaño de partícula de los ingredientes utilizados que afectan la respuesta a los aminoácidos de la dieta y limitan la respuesta máxima a la PB (Lemme et al., 2006).
Se dispone de poca información sobre modelos para predecir la respuesta de las gallinas ponedoras en función de densidades de nutrientes. Se sabe que los modelos de programación no lineal pueden ser más útiles que los modelos de programación lineal convencional en optimizar la respuesta a la densidad de energía en las formulaciones alimenticias de broilers (Guevara, 2004) y de ponedoras (Afrouziyeh et al., 2011), por lo que los niveles de energía y nutrientes no necesitan ser fijos. La respuesta del ave no es lineal sino curvilínea y experimenta el fenómeno de rendimientos decrecientes, por lo que el requerimiento no es necesariamente el máximo biológico sino el óptimo económico, el cual es variable y dinámico por depender del precio de los ingredientes y del huevo.
En este sentido, no hay modelos para estimar la respuesta del ave a diferentes densidades de aminoácidos y que, además, se hayan trabajado en términos del requerimiento óptimo económico y en base a un perfil de PI y PB. Los objetivos del presente estudio fueron desarrollar y validar un modelo para predecir el requerimiento óptimo de aminoácidos esenciales y el comportamiento productivo, utilizando los conceptos de la PI y PB en la formulación de las dietas.
MATERIALES Y MÉTODOS
Se desarrolló un modelo a partir de la literatura construyendo ecuaciones de regresión y se hizo un experimento para validarlo. El modelo predice consumo y masa de huevo a partir del nivel de proteína balanceada de la dieta.
Desarrollo del Modelo
En base al cálculo del consumo de alimento potencial y asumiendo un nivel de energía metabolizable (EM) de 2.8 kcal/g de alimento, se obtuvo el consumo de energía, con lo que se predice masa de huevo para el potencial máximo a partir de la ecuación: EM = aW0.75 + bG + cE (Abasto et al., 1997), donde a, b y c son los coeficientes de la ecuación, W0.75 es el peso metabólico de la gallina ponedora, G es la ganancia de peso (g/día) y E es la masa de huevo (NRC, 1994; Zhang y Coon, 1994; Sakomura, 2004).
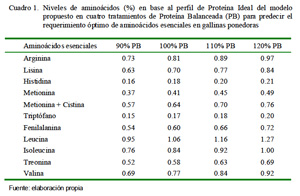
A partir de los datos obtenidos de masa de huevo, ganancia de peso y mantenimiento (promedio ponderado de los aminoácidos como porcentaje de la PI) se obtuvo el perfil de PI: 116, 100, 26, 59, 91, 24, 86, 152, 120, 83 y 110% para arginina, lisina, histidina, metionina, metionina + cistina, triptófano, fenilalanina, leucina, isoleucina, treonina y valina, respectivamente.
Para el cálculo de la PB, se fijó el porcentaje de metionina + cistina (M+C) en la dieta a partir de la deposición, relación entre M+C depositados en el huevo y los totales consumidos. A partir del perfil de PI y porcentaje de M+C (0.64%) obtenidos, se establecieron niveles de 90, 100, 110 y 120% de PB (Cuadro 1).
Dado que la respuesta del animal a la densidad de aminoácidos es curvilínea, se planteó un modelo para predecir la respuesta relativa de las aves a los niveles de PB, específicamente para predecir los valores de masa de huevo relativa y a partir de ella el consumo de alimento, para el que se utilizaron los datos del estudio sobre PB de Degussa (2006) y se generó la ecuación: Masa relativa = a + bX – cX2 (Afrouziyeh et al., 2011), donde a, b y c son los coeficientes de la ecuación, X es el nivel de PB. Luego los valores de masa de huevo y consumo de alimento predichos obtenidos con la ecuación (Afrouziyeh et al., 2011) se contrastaron (validación) con los valores de masa de huevo y consumo de alimento observados en el experimento.
Estudio Experimental
El estudio se realizó en un galpón de la granja avícola comercial San Ignacio, en la provincia de Chincha, Ica, Perú, por un periodo de 12 semanas entre abril y junio de 2010. Se utilizaron 192 gallinas ponedoras comerciales de la línea ISA Brown de 40 semanas de edad en dos módulos de jaulas tipo batería de dos pisos.
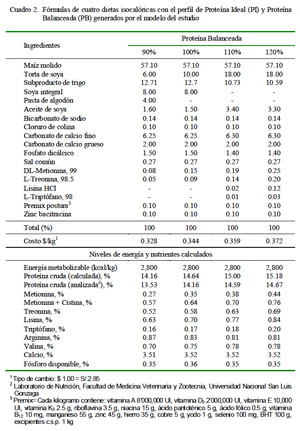
Se prepararon cuatro dietas isocalóricas (Cuadro 2) con el perfil de PI y PB generados por el modelo (Cuadro 1). Se utilizó el programa de formulación LP máxima rentabilidad (Guevara, 2004) para la elaboración de las fórmulas alimenticias. En la preparación de las dietas se utilizó una mezcladora tipo vertical con capacidad de 1000 kg. La alimentación fue ad libitum.
Las variables evaluadas fueron:
-
Producción de huevos. Se registró diariamente en cada unidad experimental. El porcentaje de producción de huevo se calculó como: N.º de huevos recolectados / Total de gallinas por unidad x 100.
-
Peso de huevos. Se pesaron los huevos en cada unidad experimental con una balanza electrónica de precisión de 0.1 g y se obtuvo el peso promedio.
-
Masa de huevo (g/d). Se obtuvo por cada unidad experimental y fue igual al porcentaje de producción x peso de huevo/100.
-
Consumo de alimento (g/ave/día). Se registró diariamente en cada unidad experimental. El consumo correspondió a la diferencia de la cantidad de alimento ofrecida y la cantidad de alimento residual en un ciclo de 24 horas.
-
Índice de conversión alimenticia. ICA = Consumo de alimento (g) / masa de huevo (g).
-
Unidad Haugh (HU). Se determinó de acuerdo a la metodología de Eisen et al. (1962). HU = 100 log(H - 1.7W0,37 + 7.57), donde H = altura del albumen en mm, W = peso del huevo (g), 7.57 = factor de corrección para la altura de albumen, 1.7 = factor de corrección para el peso del huevo.
-
Retribución económica. Se calculó tomando como base los costos de las dietas alimenticias y el ingreso por venta de huevos de cada uno de los tratamientos. Se calculó como: RE = I - C, donde RE = Retribución económica, I = Ingreso por kilogramo de huevo, C = Costos de las dietas experimentales.
En base al perfil de PI obtenido por el modelo factorial propuesto se consideraron cuatro niveles de PB como tratamientos: 90, 100, 110 y 120%. Se empleó un diseño experimental de bloques completamente al azar (DBCA) con cuatro repeticiones por tratamiento, resultando 16 unidades experimentales con 12 gallinas por cada unidad y 48 gallinas por tratamiento, con un total de 192 gallinas ponedoras. Se utilizó el modelo aditivo lineal: Yij = U + Ti + Bj + eij, donde Yij = una observación en el tratamiento i y bloque j, U = la media general, Ti = el efecto del tratamiento i, Bj = el efecto fijado del bloque j y eij = Error experimental.
Se realizó el análisis de varianza, prueba de comparación de medias de Duncan y análisis de regresión. El punto máximo de la curva se obtuvo sacando la derivada e igualando a cero la ecuación (Tedeschi, 2006). Se utilizó el procedimiento del Modelo General Lineal (GLM) de SAS (SAS Institute, 1999). Los datos obtenidos de la variable producción de huevos medidos en porcentaje fueron transformados a valores ArcoSeno.
Validación del Modelo
Los datos de masa de huevo y consumo de alimento que predecía el modelo se compararon con lo observado en este estudio. Se calculó el error de predicción del cuadrado medio (MSEP) (Tedeschi, 2006) para evaluar el modelo como indicador del error de predicción de los valores estimados a los valores observados, y en consecuencia validar la exactitud de la predicción del modelo. Este error se calculó como:
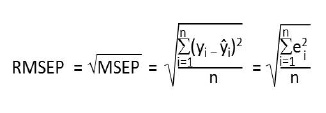
donde RMSEP = Raíz cuadrada del error de predicción del cuadrado medio, MSEP = Error de predicción del cuadrado medio, yi = valores de la masa de huevo o consumo de alimento observado, i = valores de la masa de huevo o consumo de alimento predicho, (i – wi)2 = sumatoria de los cuadrados de los residuales y n = número de observaciones.
El error del modelo se calculó expresando el error de predicción como porcentaje del promedio observado (Aguilar, 2010), de acuerdo a: Error (%) = RMSEP/ x 100, donde: RMSEP = Raíz cuadrada del error de predicción del cuadrado medio, = valor promedio de la masa de huevo o consumo de alimento observado. Se fijó un nivel del 5% como porcentaje del error del modelo como límite máximo para validar la exactitud del modelo propuesto.
RESULTADOS Y DISCUSIÓN
Modelo
Primeramente se obtuvo el requerimiento de energía en base a los datos del consumo de alimento en función de la EM requerida en Kcal/día para sostener el requerimiento de mantenimiento, crecimiento y produc ción. Para la obtención del requerimiento de EM de mantenimiento (EMm) se utilizaron los datos de Sakomura (2004) obtenidos de la regresión, donde la energía neta de mantenimiento (ENm)1 = 80 kcal/W0.75 y la eficiencia de energía neta (k)1 = 0.70. El requerimiento de EMm fue el resultado de la relación de ENm/k = 114 kcal/W0.75.
El requerimiento de EM de la ganancia (EMg) de peso se generó a partir de la composición de dicha ganancia y la eficiencia de energía (k=0.66) (Sakomura, 2004), donde se obtuvo 4.4 kcal como ENg. El requerimiento de EM para la ganancia (EMg) fue el resultado de la relación de ENg/k = 6.68 kcal/g.
El requerimiento de EM para la masa de huevo (EMh) se obtuvo de la composición química del huevo, valores de combustión de energía bruta de los lípidos, proteínas y carbohidratos, así como la eficiencia de energía (k=0.69) (Sakomura, 2004), obteniéndose 1.666 kcal como ENh. El requerimiento de EMh se calculó de la relación de ENh/k = 2.40 kcal/g.
Con los datos precedentes, y teniendo en cuenta el efecto de Tº para mantenimiento hallado por Sakomura (2004), para 22 ºC, se tiene la siguiente ecuación del requerimiento de energía:

donde EM = Energía Metabolizable en Kcal/ día, Tº = temperatura ambiental, W= peso corporal (kg), dW = ganancia del peso corporal (g/día) y EE = masa de huevo (g). La masa de huevo fue 58 g (generado por la ecuación del consumo de energía), el peso corporal de 1940 g y una ganancia de peso corporal de 1.67 g/gallina/día, obteniéndose el requerimiento de EM (Kcal/día) = 337 y considerando una dieta con 2.8 Mcal/kg se estimó un consumo de alimento de 120 g/día.
En segundo lugar y en base al estudio sobre PB de Degussa (2006) se obtuvo el modelo para predecir la masa de huevo básicamente y también el consumo de alimento a partir del 100 % de la PB:

donde y1 = Masa de huevo relativa, y2 = Consumo de alimento relativo, X = Nivel de PB.
Estudio Experimental
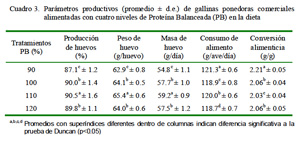
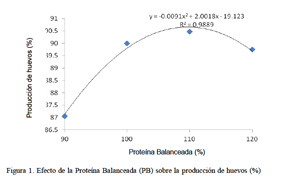
El análisis de regresión para el requerimiento de PB siguió una tendencia cuadrática. La producción de huevos fue significativamente mayor (p<0.05) para el grupo de ponedoras con PB de 110%, siendo este nivel el requerimiento de PB para el máximo biológico, según el análisis de regresión (Cuadro 3; Fig. 1).
Esta mejor respuesta se explicaría por el efecto de M+C y su relación a la lisina para maximizar la producción de huevo. En base al modelo propuesto, este nivel de PB corresponde a un nivel de 0.70% de M+C, 0.77% de lisina y una relación M+C/lisina de 91% en la dieta, valores cercanos a los estudiado por Novak et al. (2006) con un nivel de M+C de 0.69%, lisina 0.76% y una relación M+C/lisina de 91% y por Togashi et al. (2002) con una relación M+C/lisina de 91.6%, que encontraron la máxima producción de huevos. El análisis de regresión para el peso del huevo siguió una tendencia cuadrática, similar a la regresión para la producción de huevos.
El peso del huevo fue significativamente superior en el grupo de ponedoras con PB de 110% (p<0.05), siendo este nivel el requerimiento de PB para el máximo biológico, según el análisis de regresión. El nivel y la relación de M+C/lisina explicaría este resultado, ya que los aminoácidos azufrados influyen sobre la mejora del peso del huevo, tal como lo reporta Shafer et al. (1996), quienes encontraron un incremento en el peso del huevo conforme incrementaban el consumo de metionina desde desde 326 a 512 mg por gallina/ día. No obstante, un aumento en la relación M+C/lisina también podría afectar esta variable, pues Jordao et al. (2006) encontraron la más baja respuesta del peso de huevo con una relación M+C/lisina de 91.7%.
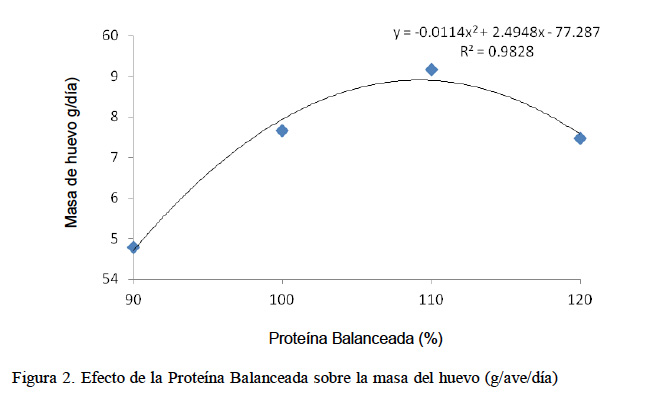
La masa de huevo fue significativamente superior para el grupo de ponedoras con PB de 110% (p<0.05). El requerimiento de PB para el máximo biológico en el análisis de regresión fue de 109.4%, respuesta que siguió una tendencia cuadrática (Fig. 2). En los otros niveles, la respuesta de la masa de huevo disminuye, lo que podría deberse al menor consumo de nutrientes y menor eficiencia de su utilización (Baker et al., 2002). Este resultado concuerda con el estudio de Novak et al. (2006), quienes encontraron la máxima respuesta de masa de huevo con niveles de M+C de 0.69%, lisina de 0.76% y una relación M+C/lisina de 91% en la dieta
El consumo de alimento fue significativamente mayor para el grupo de ponedoras con PB de 90% (p<0.05). En el análisis de regresión, donde el efecto siguió una tendencia cuadrática, se observa una disminución del consumo de alimento conforme aumenta el nivel de PB de la dieta. Togashi et al. (2002) encontraron, asimismo, una disminución del consumo de alimento de 126.6 g/ave/ día (0.55% M+C) a 122.69 y 120.45 g/ave/ día (0.60% y 0.65% M+C). Es posible que las gallinas ponedoras fijen su consumo en función del nivel de aminoácidos de la dieta cuando los requerimientos de aminoácidos no son satisfechos, independiente del nivel de energía (Veldkamp et al., 2005), lo que hizo que aumentase el consumo cuando los niveles de aminoácidos eran bajos.
El índice de conversión alimenticia fue significativamente mejor para el grupo de gallinas ponedoras que consumieron la dieta con 110% de PB (p<0.05), siendo este nivel el requerimiento de PB para el máximo biológico de acuerdo al análisis de regresión que siguió una tendencia cuadrática. Esta respuesta se aproxima a los resultados de Togashi et al. (2002), quienes encontraron la mejor conversión alimenticia para la relación M+C/ lisina de 91.6%.
La Unidad Haugh del huevo no fue significativamente afectada por los niveles de PB. Asimismo, Togashi et al. (2002) tampoco encontraron un efecto importante de los niveles de M+C sobre esta variable.
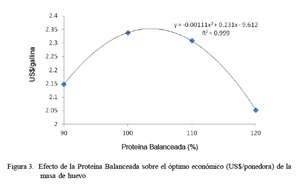
En el análisis de regresión se encontró una relación cuadrática significativa entre los niveles de PB y la retribución económica (US$/ponedora), siendo el nivel de 104% de PB el requerimiento para el óptimo económico de la masa de huevo (Fig. 3). Al comparar este nivel con el requerimiento de 109.4% de PB para el máximo biológico, se deduce que el mejor comportamiento productivo (máximo biológico) no necesariamente significó una máxima rentabilidad (óptimo económico). Es así que las especificaciones de nutrientes en general y la especificación de aminoácidos en particular deberían ser ajustadas a las condiciones económicas incluyendo el costo del alimento y precio del huevo (Lemme, 2009); asimismo, mientras que el nivel absoluto de aminoácidos puede cambiar con la situación económica, la relación de la proteína ideal entre los aminoácidos permanece igual.
Este resultado cuestionaría el método de la línea quebrada para determinar el requerimiento de nutrientes ya que la respuesta es curvilínea y experimenta el fenómeno de los rendimientos decrecientes. Las dietas formuladas para maximizar rentabilidad, utilizando el concepto de los rendimientos decrecientes, y el análisis marginal de la economía podrían tener un resultado efectivo desde el punto de vista del óptimo económico (Gahl et al., 1994), ya que este concepto de los rendimientos decrecientes es interpretado económicamente, por lo que el mejor nivel de alimentación para un nutriente no es el requerimiento para un máximo comportamiento productivo (Pesti et al., 2009).
El mejor nivel de alimentación es la concentración de nutrientes que maximiza las ganancias económicas, ya que los requerimientos de nutrientes para un máximo comportamiento productivo no están influenciados por el precio del huevo y alimento (Roland et al., 1998). Por consiguiente, para optimizar las ganancias económicas, diferentes niveles de PB deben ser establecidos conforme cambian los precios del huevo y del alimento.
Validación del Modelo
El error del modelo fue de 4.71% para la masa de huevo y de 2.44% para el consumo de alimento, lo que valida el modelo propuesto. Este modelo es dinámico y predice el nivel de PB óptimo para sostener una máxima masa de huevos y óptimo económico. Este enfoque difiere considerablemente del convencional (requerimientos fijos de los aminoácidos). La validación de este modelo en términos de PI y PB para la masa de huevo es la base para que su aplicación en la industria de ponedoras comerciales contribuya a precisar los niveles óptimos de los aminoácidos en la dieta que permita tomar decisiones económicas y establecer mejores y más rentables programas de alimentación. Rondón et al. (2002) consideran que los modelos matemáticos permiten la estimación de los requerimientos nutricionales de forma más precisa, así como establecer los mejores programas de alimentación de acuerdo con las situaciones del mercado para optimizar los retornos económicos.
CONCLUSIONES
-
La producción de huevos, peso y masa de huevo, consumo de alimento y conversión alimenticia tuvieron la mejor respuesta con el nivel de 110% de PB y el requerimiento de PB para el máximo biológico y óptimo económico fue 109% y 104%, respectivamente.
-
El modelo desarrollado basado en el concepto de PI y PB predice adecuadamente el requerimiento de M+C y fue validado a nivel experimental indicando que la simulación del efecto de la PB sobre la performance es adecuado.
LITERATURA CITADA
1. Abasto P, Aguilar C, Vera, R, García F. 1997. Modelo de simulación para la gestión estratégica de sistemas de engorda de corderos Suffolk (secano costero- chile). Proyecto FONDEF D97 I2008. Santiago de Chile: Pontificia Universidad Católica de Chile. 6 p.
2. Afrouziyeh M, Shivazad M, Chamani M, Dashti G, Amirdahri S. 2011. Use of nonlinear programming to determine the economically optimal energy density in laying hens diet during phase 2. J Appl Poultry Res 20: 50-55.
3. Aguilar FA. 2010. Modelos matemáticos no lineales como herramienta para evaluar el crecimiento de tilapia roja (Oreochromis spp) y tilapia nilótica (Oreochromis niloticus var. chitralada) alimentadas con dietas peletizadas o extruidas. Tesis de Magíster. Colombia: Univ Nacional de Colombia. 145 p.
4. Baker DH, Batal AB, Parr TM. 2002. Ideal ratio (relative to lysine) of tryptophan, threonine, isoleucine and valine for chicks during the second and third week posthach. Poultry Sci 81: 485-494.
5. Bregendahl K, Roberts SA. 2009. The ideal amino acid profile for laying hens. [Internet]. Available in: http://www.intervet.co.th/binaries/53%20The%20Ideal%20Amino%20Acid%20Profile%20for%20Laying%20Hens_tcm125-168610.pdf
6. Campos A, Salguero S, Albino L, Rostagno H. 2008. Aminoácidos en la nutrición de pollos de engorde: Proteína ideal. En: III CLANA. México: Congreso del Colegio Latino-Americano de Nutrición Animal. 16 p.
7. Degussa. 2006. Increasing balanced protein intake improved laying hen performance independent of energy intake. In: Boletin Degussa, Facts and Figures. Poultry N.° 1557.
8. Eisen EJ, Bohren BB, Mckean HE. 1962. The Haugh unit as a measure of egg albumen quality. Poultry Sci 41: 1461-1468.
9. Filev J, Sokarovski J, Kon-popovska M. 1990. Feed formulations for laying hen. Options Méditerranéennes, Série A 7: 55-63.
10. Fisher C, Morris, TR, Jenning SRC. 1973. A model for the description and prediction of the response of laying hens to amino acid intake. Br Poultry Sci 14: 469-484.
11. Gahl MJ, Crenshaw TD, Benevenga NJ. 1994. Diminishing returns in weight, nitrogen, and lysine gain of pigs fed six levels of lysine from three supplemental sources. J Anim Sci 72: 3177-3187.
12. Guevara VR. 2004. Use of nonlinear programming to optimize performance response to energy density in broiler feed formulation. Poultry Sci 83: 147-151.
13. Halas V, Babinsky L. 2000. Modelling of performance and protein and fat deposition in pigs: a review. Krmiva 42: 251-260.
14. Hurwitz S, Bornstein S. 1973. The protein and amino acid requirement of laying hens: suggested models for calculation. Poultry Sci 52: 1124-1134.
15. Joly P. 2008. Reevaluation of amino acids requirements for laying hens. ISAHendrix Genetics France. [Internet], [02 octubre 2009]. Disponible en: www.engormix.com
16. Jordao Filho J, Vilar da Silva JH, Lindolfo da Silva E, Gomes RML, Dantas TD, Boa-Viagen C. 2006. Exigencias nutricionais de metionina + cistina para poedeiras semipesadas do inicio de producao até o pico de postura. Rev Bras Zootec 35 (Suppl1): 1063-1069.
17. Lemme A, Wijtten PJA, Van Wichen J, Petri A, Langhout DJ. 2006. Responses of male growing broilers to increasing levels of balanced protein offered as coarse mash or pellets of varying quality. Poultry Sci 85: 721-730.
18. Lemme A. 2009. Amino acid recommendation for laying hens. Lohman Inf 44(2): 21-32.
19. Londoño JA, Mejía HP, Rivera RS, Vargas JE. 2002. Validación del modelo DRASTIC para simular producción de leche y formular raciones balanceadas en sistemas lecheros de la región andina. Medellín: Grupo de Investigación ASPA. Universidad Nacional, Medellín. 17 p.
20. [NRC] National Research Council. 1994. Nutrient requirements of poultry. 9th ed. Washington, DC: National Academic Press. 155 p.
21. Novak C, Yakout HM, Scheideler SE. 2006. The effect of dietary protein level and total sulfur amino acid:lysine ratio on egg production parameters and egg yield in Hy-Line W-98 hens. Poultry Sci 85: 2195-2206.
22. Pesti GM, Vedenov D, Cason JA, Billard L. 2009. A comparison of methods to estimate nutritional requirements from experimental data. Br Poultry Sci 50: 16-32.
23. Roland DA, Bryant MM, Zhang JX. 1998. Econometric feeding and management 1. Maximizing profits in Hy-line W-36 hens by optimizing total sulfur amino acid intake and environmental temperature. J Appl Poultry Res 7: 403-411.
24. Rondón EOO, Murakami AE, Sakaguti ES. 2002. Modelagem computacional para producao es pesquisa em avicultura. Rev Bras Cien Avicola 4(1): 199-207.
25. ROSS Nutrition Suplement. 2009. Protein and amino acids. [Internet], [08 Noviembre 2009]. Available in: http://www.poultryhub.org/wp-content/uploads/2012/06/Ross_Nutri-tion_Supplement.pdf
26. Sakomura NK. 2004. Utilization of the factorial model to determine the nutritional requirements of poultry. En: II Simpósio Internacional sobre exigéncias nutricionales de aves e suinos. Brasil. 38 p.
27. Santomá G. 1991. Necesidades proteicas de las gallinas ponedoras: Nutrición y alimentación de gallinas ponedoras. Madrid: Ed Mundi-Prensa. 263 p.
28. SAS. 1999. User´s Guide: Statistics. Cary, NC. USA: SAS Institute Inc. 230 p.
29. Schutte JB, De Jong J. 1998. Ideal amino acid profile for poultry. Options Mediterranéennes 9: 259-263.
30. Tedeschi LO. 2006. Assessment of the adequacy of mathematical models. Agr Syst 89: 225-247.
31. Togashi CK, Brandao JF, Ribeiro RTNS, Melo CLS. 2002. Determinacao de niveis de metionina + cistina para poedeiras semi-pesadas alimentadas com racoes contendo levedura seca (Saccharomyces cerevisae). Rev Bras Zootec 31: 1426-1433.
32. Veldkamp T, Kwakkel RP, Ferket PR, Verstegen MWA. 2005. Growth responses to dietary energy and lysine and low ambient temperature in male turkeys. Poultry Sci 84: 273-282.
33. Zhang B, Coon CN. 1994. Nutrient modeling for laying hens. J Appl Poultry Res 3: 416-431.
Recibido: 29 de octubre de 2012
Aceptado para publicación: 12 de abril de 2013