INTRODUCCIÓN
Los análisis de correlación son métodos estadísticos descriptivos utilizados en investigación de nivel relacional (Badii et al., 2007), con los que se estima la magnitud y define la tendencia de la relación entre variables. Los métodos de correlación de Pearson (CP) y Spearman (CS) son técnicas bivariadas que se emplean en circunstancias multivariadas para la explicación de diversos fenómenos relacionados en el campo animal y vegetal (Restrepo y Gonzales, 2007). En las correlaciones de Pearson [r] (Pearson, 1896) y de Spearman [rs] (Spearman, 1904), los procedimientos guardan relación con la naturaleza de las variables utilizadas. El primer coeficiente es un estadístico paramétrico que requiere absolver previamente el cumplimiento de varias premisas o supuestos, especialmente el de normalidad bivariada para las variables analizadas (Hernández et al., 2018), en tanto el segundo es un estimador no paramétrico utilizado en variables que no necesariamente cumplen criterio de normalidad (Sánchez-Villegas et al., 2020).
El coeficiente de correlación de Pearson (CCP) es un estadístico frecuentemente utilizado en diversas áreas del quehacer científico. Hernández et al. (2018) explican el uso indebido que se le da a esta herramienta estadística, especialmente en aquellos escenarios en los que debe ser interpretada correctamente, o en los que se tienen que comprobar las suposiciones matemáticas que la sustentan. Estudios de investigación que determinan la relación de asociación entre caracteres de la fibra de camélidos sudamericanos domésticos y silvestres (Lupton et al., 2006; Manso, 2011; Díaz, 2014; Pariona, 2014; Vásquez et al., 2015; Machaca et al., 2017; Calsín, 2017, Tapia, 2018) refieren al Coeficiente de Correlación de Pearson; sin embargo, ninguno indica que previa su determinación se haya verificado el cumplimiento de supuestos que otorgan validez al coeficiente; más aún es imprescindible que al menos una de las variables tenga una distribución Normal si el objetivo es realizar inferencias válidas.
Otro aspecto importante a considerar en la determinación de los CCP y CCS es el tamaño de la muestra, los cuales deben ser adecuados si se desea determinar parámetros confiables recurriendo a procedimientos metodológicos adecuados (Henríquez et al., 2012). Lo evidente es que la determinación del tamaño muestral no siempre se presenta en trabajos de investigación.
La estima de los coeficientes de correlación no únicamente implica estimación puntual, sino que también requiere de intervalos de confianza. Estos y la significación estadística del coeficiente son dos caras de una moneda, dado que se complementan, pero no se sustituyen (Santabarbara, 2019). Una buena práctica requiere que, para tomar decisiones de investigación acertadas, ambos aspectos deben ser considerados. Para que los estimados a través de intervalos de confianza y la significancia del CCP sean válidos, se precisa que ambas variables tengan una distribución Normal bivariada (Camacho, 2008; Triola, 2009), ya que, de no acreditar el cumplimiento de estos supuestos, los resultados no serían confiables y, por lo tanto, las interpretaciones tampoco serían válidas.
El objetivo del estudio fue determinar valores de los CCP y CCS y su significancia para pares de características físicas y textiles de la fibra de alpaca, así como estimar intervalos de confianza que contribuyan a definir el mejor procedimiento estadístico de la relación de asociación entre estos caracteres.
MATERIALES Y MÉTODOS
Lugar del Estudio
Se utilizaron 22 543 muestras de vellón obtenidas de alpacas Huacaya, de diversa edad y de ambos sexos, procedentes de todas las provincias de la Región Puno, excepto Yunguyo. Se incluyeron muestras de 55 distritos y 362 comunidades distribuidas a lo largo de los dos sectores de la Zona Agroecológica Puna: Puna Seca y Puna Húmeda, de la Región Puno (ALT-PNUD, 2001). El sistema de manejo fue de tipo extensivo, con alimentación a base de pastos naturales de praderas altoandinas.
Análisis de Fibra
Las muestras de fibra fueron analizadas en el Laboratorio de Fibras del Proyecto Especial Camélidos Sudamericanos (PECSA) del Gobierno Regional Puno, utilizando un equipo OFDA 2000, instrumento diseñado y propuesto para la medición de características en fibra grasienta, siguiendo la propuesta metodológica de Brims et al. (1999). En cada muestra se determinaron variables que evidencian características físicas y textiles: Diámetro medio de la fibra (MDF), Desviación estándar del diámetro de fibra (DE), Coeficiente de variabilidad del diámetro de fibra (CDV), Coarse Edge Micron (CEM), porcentaje (%) de fibras menores a 15 µm (FINO15), Factor de confort (FDEC), Finura de hilado (FDEH), largo de la mecha (LMECHA), Finest point from the tip (FPFT) e Índice de curvatura (CRV).
Análisis Estadístico
El Coeficiente de Correlación de Pearson fue obtenido por,
parámetro que en términos de su estadístico se expresa según (Restrepo y Gonzales, 2007), como
La significancia del Coeficiente de Correlación (r) de Pearson implicó la aplicación de la prueba de significancia estadística de t para el CCP, bajo el supuesto de que ρ es el verdadero valor del CCP. El estadístico
prueba la Ho: r = 0, basado en una aproximación a la distribución de t de Student, el cual es comparado con la distribución de t de Student con n-2 grados de libertad (Looney, 2015). Operativamente, para la determinación del CCP y la significancia de estos en términos probabilísticos (p value) se recurrió al procedimiento Corr del SAS (2013).
Para la determinación de los intervalos de confianza para el Coeficiente de Correlación de Pearson se utilizó la transformación Z de Fisher, transformando las r correlaciones muestrales en una nueva variable aleatoria que se distribuye aproximadamente normal, variable que puede ser usada para derivar un intervalo de confianza aproximado para el verdadero valor del Coeficiente de correlación de Pearson (Looney, 2015). Así, asumiendo normalidad asintótica de esta última, se determinó un intervalo para el coeficiente de correlación poblacional (ρ) (Krishnamoorthy y Xia, 2007). Fisher (Kendall y Stuart, 1961) demostró que cuando se toman muestras de tamaño mayor a 25 de una distribución normal bivariada con un coeficiente de correlación ρ, la tangente hiperbólica inversa de la Correlación de la muestra tiene una distribución aproximadamente normal. La Tangente hiperbólica in- versa del coeficiente de correlación fue obtenida a través de la función ATANH de la hoja electrónica Excel, así como la tangente del producto: ATANH por
fue obtenida por la función TANH de la misma hoja de cálculo. Los límites de confianza fueron obtenidos por las ecuaciones siguientes:
(Stuart y Ord, 1987), para el Límite inferior (LI) y Límite superior (LS), respectivamente.
Coeficiente de Correlación de Rangos Ordenados (rs) de Spearman (CCS)
Fueron determinados a través de:
(Restrepo y Gonzales, 2007), donde pho= es el símbolo paramétrico del CCS, y rs su estadístico. Ecuación que implícitamente corrige el efecto del número grande de rangos (Barreto, 2011), debido a la existencia de va- lores iguales (empatados) dentro de cada variable. Operacionalmente este fue determinado recurriendo al procedimiento: Proc Corr Spearman, del Software SAS.
Por el gran tamaño de muestra que se utilizó y que inviabiliza el uso de la Tabla: «Significancia de la correlación de Spearman», para determinar la Significancia del Coeficiente de Correlación de Spearman, se estandarizaron los valores de rho de Spearman a un valor de t de Student, la misma que se distribuye con n-2 grados de libertad. El estadístico de t se utilizó para someter a prueba la hipótesis Ho: rho=0, dado que Ho sea cierto. El valor de la probabilidad de significancia para el CCS fue determinado a través de:
donde rs es el coeficiente de correlación de Spearman, t fue contrastado con valores de la Tabla: «Percentiles de la distribución de t de Student» para infinitos grados de libertad, para una prueba bilateral.
El Intervalo de confianza para el Coeficiente de Correlación de Spearman fueron determinados por la aproximación de Ruben (Boomsma, 1977), recurriendo al Archivo RHO_CI del programa SAS®, programa específico para calcular límites de confianza de Ruben. Ruben (1966) demostró que:
(Sun y Wong, 2007) está distribuida como normal estandarizada, para n>2, donde:
Consecuentemente, los intervalos de confianza para ñ, con un nivel de confianza (1-0.05), pueden ser fácilmente obtenidos de la distribución asintótica Zhr.
Pruebas de Normalidad para Caracterís- ticas Físicas y Textiles de la Fibra
Se ejecutaron pruebas de normalidad de Kolmogórov-Smirnov y de Ryan-Jonier al objeto de determinar normalidad en las distribuciones de cada una de las características del presente estudio. Para este efecto, se utilizaron los Software SAS 9.4 y Minitab 17.
RESULTADOS
El Cuadro 1 presenta los CCP, niveles de significancia e intervalos de confianza para la relación de asociación entre pares de características físicas y textiles de la fibra de alpacas, evidenciándose con claridad que algunos valores de los CCP (r) son positivos y otros son negativos.
Cuadro 1 Coeficientes de Correlación de Pearson (r) para características físicas y textiles de la fibra de alpacas de la Región Puno
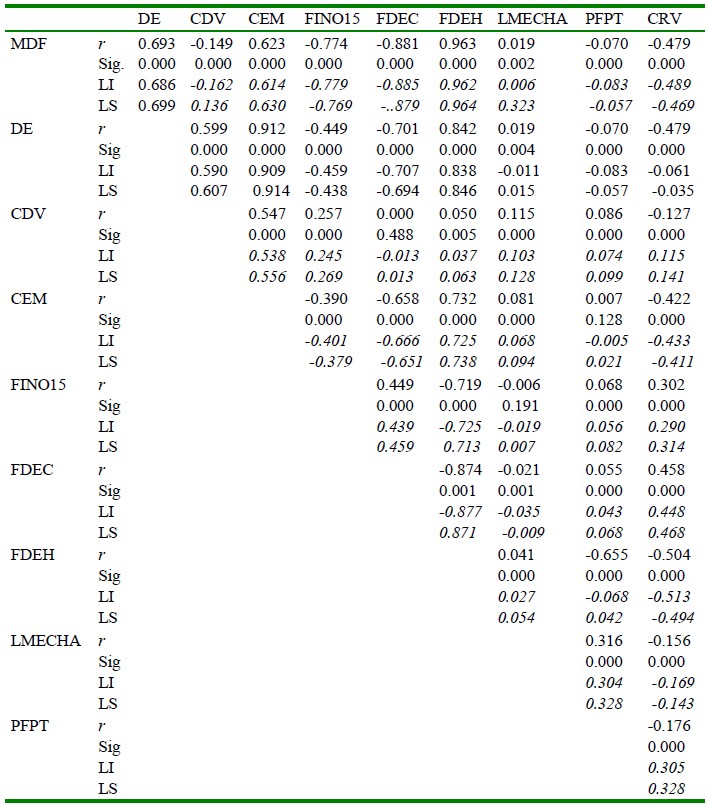
r= Coeficiente de Correlación de Pearso, Sig= Significación estadística del coeficiente de correlación de Pearson, LI = Límite inferior de r, LS = Límite superior de r
Diámetro medio de la fibra (MDF), Desviación estándar del diámetro de fibra (DE), Coeficiente de variabilidad del diámetro de fibra (CDV), Coarse Edge Micron (CEM), porcentaje (%) de fibras menores a 15 µm (FINO15), Factor de confort (FDEC), Finura de hilado (FDEH), largo de la mecha (LMECHA), Finest point from the tip (FPFT) e Índice de curvatura (CRV)
Los valores de r, en términos absolutos, se encuentran en un rango de 0.000 a 0.963, como mínimo y máximo, respectivamente, de los cuales se deduce la magnitud de la relación lineal entre variables, los que pueden ser calificados como: Correlación Nula (0), Muy baja (± 0.01 a ± 0.10), Débil (± 0.11 a ± 0.50), Media (± 0.51 a ± 0.75), Considerable (± 0.76 a ± 0.90), Muy fuerte (± 0.91 a ± 0.99) y Perfecta (1.00) (Mondragón, 2014). Para el caso específico de r = 0.000, no necesaria- mente implica que no exista relación entre estas variables, sino que la relación podría ser no es lineal, y para el caso de r = 0.963, se deduce que la relación describe una función aproximadamente lineal.
De manera similar, en el Cuadro 1 se observa la significancia estadística de r. donde la mayoría de los valores son de orden p<0.000, excepto para algunos que muestran una significancia con valores p cercanos a cero: MDMF-LMECHA (0.002), DE-LMECHA (0.004), o muy bajos como CEM- PFPT (0.128), FINO15-LMECHA (0.193), y otros moderados como CDV-FDEC (0.488); valores que permiten discernir si las variables están relacionadas o que dicha relación es consecuencia del azar.
Es importante precisar que el CCP paramétrico (ρ) puede ser estimado por intervalos de confianza; en efecto, el Cuadro 1 presenta intervalos de confianza para los CCP definidos por los límites inferior (LI) y superior (LS), respectivamente, a un nivel de confianza de (1-0.05). Es evidente que cada coeficiente de correlación se encuentra dentro de estos límites; además, en la mayoría de los casos el rango entre estos es muy estrecho, lo que le otorga fidelidad del valor de r. Así mismo, evidencian cierta asimetría respecto del valor de r.
El Cuadro 2 presenta los Coeficientes de Correlación de Spearman (rs), niveles de significancias e intervalos de confianza para pares de características físicas y textiles de la fibra de alpacas. Los rs asumen valores diferentes, precedidos de un signo positivo o negativo, dentro de un rango de 0.003 a 0.977 en términos de valores absolutos. Estos también pueden ser calificados conforme a lo establecido por Mondragón (2014). La evidencia de mayor relación lineal está definida por la correlación entre MDMF-FDEH (0.977) y la que presenta casi nula relación lineal es la correlación entre MDMF- LMECHA (0.003).
Cuadro 2 Coeficientes de Correlación de Spearman (rs) para características físicas y textiles de la fibra de alpacas de la Región Puno
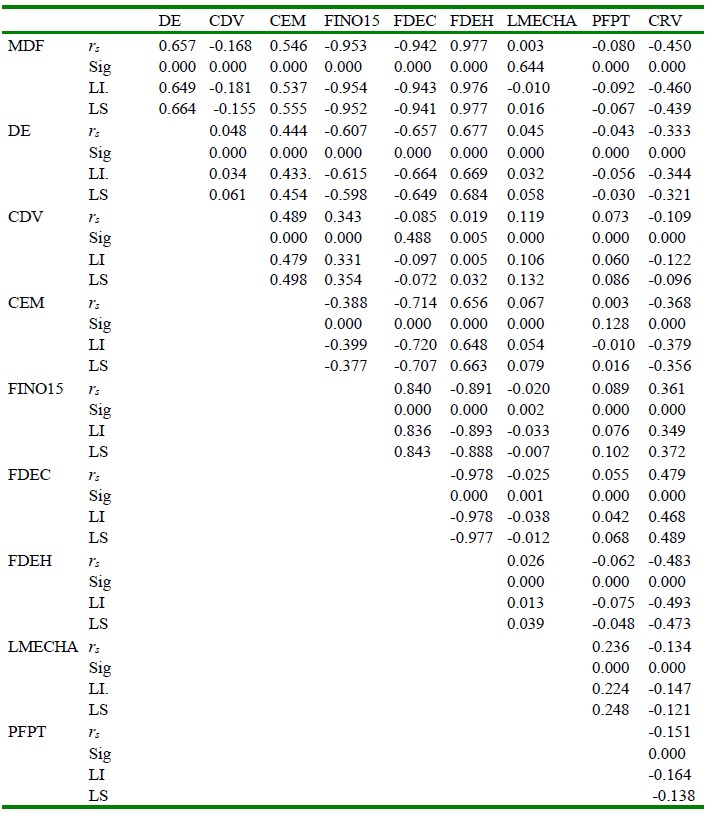
rs = Coeficiente de Correlación por rangos de Spearman, Sig = Significación estadística del coeficiente de correlación de Spearman, LI = Límite inferior de ρ, LS = Límite superior de ρ
Diámetro medio de la fibra (MDF), Desviación estándar del diámetro de fibra (DE), Coeficiente de variabilidad del diámetro de fibra (CDV), Coarse Edge Micron (CEM), porcentaje (%) de fibras menores a 15 µm (FINO15), Factor de confort (FDEC), Finura de hilado (FDEH), largo de la mecha (LMECHA), Finest point from the tip (FPFT) e Índice de curvatura (CRV)
Respecto a la significación estadística del Coeficiente de Correlación de Spearman, se observa que casi la totalidad de coeficientes de correlación asumen un valor de 0.000, excepto las correlaciones entre MDMF-LMECHA (0.644), CDV-FDEC (0.488), CEM-PFPT (0.128), que evidencian que entre las características consideradas no existe una relación lineal, con un elevado nivel de probabilidad.
El Cuadro 2 presenta, además, los intervalos de confianza para cada CCS, donde es obvio indicar que entre estos límites se encuentra el valor de coeficiente de correlación con una confiabilidad del 95.0% para esta circunstancia. Un aspecto meritorio de precisar es el hecho de que la mayoría de los valores de los CCP son mayores que aquellos de los CCS para las mismas relaciones de asociación.
El Cuadro 3 presenta pruebas de normalidad para características físicas y textiles de la fibra de las alpacas del estudio. Una implicancia genérica de la interpretación de estos estadísticos para todas las variables es que ninguna se distribuye normalmente desde un punto de vista estrictamente estadístico, evaluados por ambos procedimientos de prueba.
Cuadro 3 Estadísticos de Kolmogorov-Smirnov (D) y Ryan-Jonier (R-J) y significancias (Pr>D) y (Pr>r-j) para características físicas y textiles de la fibra de alpacas de la Región Puno, Perú
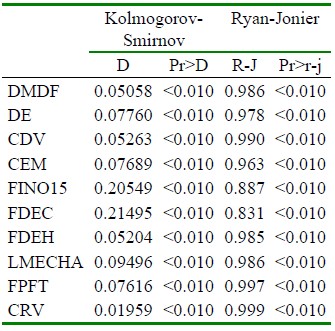
Pr>D = p value del estadístico de Kolmogorov- Smirnov, Rr> r-j= p value del estadístico de Ryan-Jonier
Diámetro medio de la fibra (MDF), Desviación estándar del diámetro de fibra (DE), Coeficiente de variabilidad del diámetro de fibra (CDV), Coarse Edge Micron (CEM), porcentaje (%) de fibras menores a 15 µm (FINO15), Factor de confort (FDEC), Finura de hilado (FDEH), largo de la mecha (LMECHA), Finest point from the tip (FPFT), Índice de curvatura (CRV)
DISCUSIÓN
Coeficiente de Correlación de Pearson
Los CCP determinados proporcionan información sobre la magnitud de la relación lineal entre pares de caracteres físicos y textiles de la fibra de alpacas; asimismo, definen la fuerza, la dirección, sentido o tendencia de la relación existente entre variables (Hernández et al., 2018), categorizados según Mondragón (2014).
Varios son los reportes científicos a nivel regional, nacional e internacional, que presentan resultados de la relación de asociación entre variables para características de la fibra de alpacas a través del CCP (Cuadros 4 y 5). En estos cuadros se evidencia que los valores reportados por estos investigadores, para una misma relación de variables es disímil. Asimismo, también evidencia diferencias por efecto del sexo, edad y raza en algunos casos. A esta realidad, se adicionan los resultados obtenidos en el presente estudio, hecho que contribuye a generar mayor variabilidad en los valores de los CCP para la relación entre variables. Sin embargo, un aspecto congruente de los resultados obtenidos en el estudio y los referidos por otros trabajos de investigación es la tendencia de la relación funcional.
Cuadro 4 Coeficientes de Correlación de Pearson (r), referencias y tamaño de muestra, entre características físicas y textiles de la fibra de alpacas (Parte I)
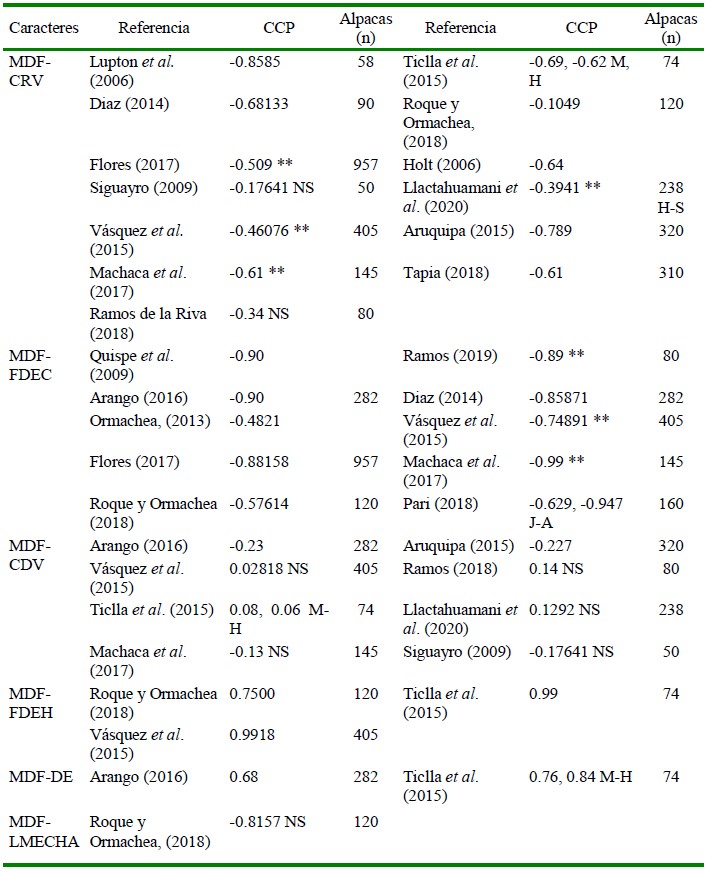
MDF = Media del diámetro de fibra, CRD = Índice de curvatura, FDEC = Factor de confort, CDV = Coeficiente de variabilidad del diámetro de fibra, FDEH = Finura de hilado, DE = Desviación estándar del diámetro de fibra, LMECHA= Largo de mecha
M-H = Machos y hembras, J-A = Jóvenes y adultos
** = Altamente significativo, NS= No significativo
Cuadro 5 Coeficientes de Correlación de Pearson (r), referencias y tamaño de muestra, entre características físicas y textiles de la fibra de alpacas (Parte II)
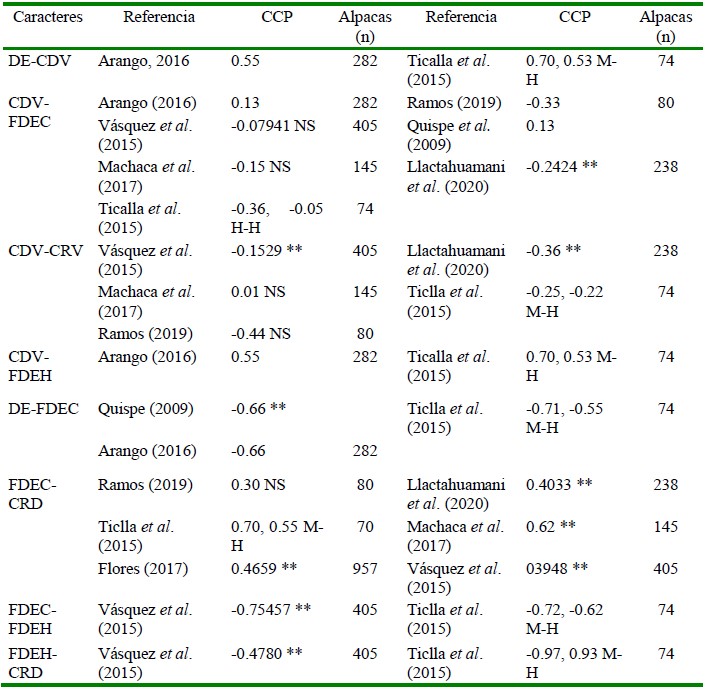
MDF = Media del diámetro de fibra, CRD = Índice de curvatura, FDEC = Factor de confort, CDV = Coeficiente de variabilidad del diámetro de fibra, FDEH = Finura de hilado, DE = Desviación estándar del diámetro de fibra, LMECHA= Largo de mecha
M-H = Machos y hembras, J-A = Jóvenes y adultos
** = Altamente significativo, NS= No significativo
Una de las razones que explica este comportamiento es el posible incumplimiento de los supuestos de normalidad bivariada, homocedasticidad e independencia (Manzo, 2011; Díaz, 2014; Machaca et al., 2017; Vásquez et al., 2015; Lupton et al., 2006). En las investigaciones que determinan CCP y ejecutan inferencias acerca del parámetro ñ no hacen referencia implícita que se ha verificado el cumplimiento previo de los supuestos referidos. En ausencia de normalidad es de esperar que se obtengan resultados diferentes a la realidad (Sánchez y Borges, 2005). Consecuentemente, los valores así determinados carecen de precisión, dado que muchos de los métodos estadísticos inferenciales se basan en la normalidad de la distribución de la variable. De no serlo, los contrastes ejecutados no son válidos, incluyendo el análisis de correlación propuesto por Pearson (Morales y Rodríguez, 2016). Paradójicamente, esta circunstancia también ocurrió con las variables del presente estudio, por cuanto que, a sabiendas de que sus distribuciones no cumplen estrictamente la normalidad, se determinó los CCP. Por otro lado, muestras grandes tienden a disminuir los efectos perjudiciales de no normalidad (Morales y Rodríguez, 2016), y en el caso del presente estudio se utilizó un tamaño de muestra muy grande, lo cual este efecto queda atenuado en algunas de las variables.
La Figura 1 presenta histogramas de frecuencias para las características DMDF, CRV, DE, FDEH, CEM y CDV. Una apreciación intuitiva de estas permite percibir una distribución normal, aunque estrictamente no lo son acorde con las pruebas de Kolmogorov-Smirnov y Ryan Jonier. Sin embargo, aceptando con cierta relatividad que se aproximan a una normal, los valores de los CCP entre estas características podrían ser considerados aproximaciones de parámetros verdaderos y válidos; al objeto de pruebas de hipótesis e inferencias a cerca de r (Sánchez y Borges del Rosal, 2004).
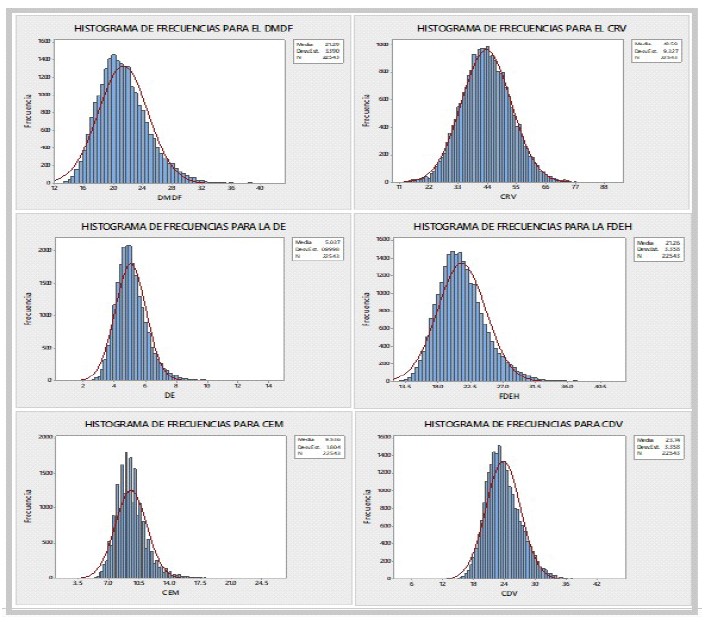
Figura 1 Histogramas de características físicas y textiles de la fibra de alpacas de la Región Puno, Perú: Diámetro Medio del Diámetro de fibra, Índice de Curvatura, Desviación Estándar del Diámetro de Fibra, Finura de Hilado, Coarse Edge Micron y Coeficiente de Variabilidad del Diámetro de Fibra
El tamaño de muestra es otra de las razones que explica la diversidad de valores de los CCP para una misma relación de variables en los trabajos publicados que relacionan caracteres de la fibra de alpacas, como se evidencia en los cuadros 4 y 5. Se aprecia que el tamaño de muestra es pequeño o relativamente pequeño en la mayoría de las citas. Díaz y Fernández (2002) sostienen la necesidad de precisar el tamaño de la muestra requerida para la ejecución de un estudio correlacional, de modo que permita al investigador conocer el número mínimo de individuos a estudiar para detectar como significativo una magnitud determinada. De no hacerlo conlleva a realizar estudios con un número insuficiente de casos y cometer Error de Tipo II; es decir, no detectar una correlación significativa cuando realmente existe.
Enríquez et al. (2012) afirman que el tamaño de la muestra para la determinación de r, a un nivel de significación dado depende solo del valor de ρ; es decir, será mayor cuando ρ esté próximo a cero y disminuirá cuando ρ tiende a uno; aspecto que en el presente estudio no se tuvo en cuenta, debido a la carencia de valores paramétricos referenciales de los CCP. Afortunadamente, los CCP entre algunas características, producto de la presente investigación, podrían considerarse aproximaciones de parámetros verdaderos y válidos que ayuden a definir un tamaño de muestra óptimo para estos análisis.
La Figura 2 presenta histogramas de frecuencias para las características FINO15, FDEC, FPFT y LMECHAS. Es axiomático observar que estas variables no presentan una distribución Normal. Se evidencian comportamientos asimétricos de forma, así como transgresiones en el apuntamiento, lo cual implica que los CCP obtenidos entre estos caracteres no sean confiables.
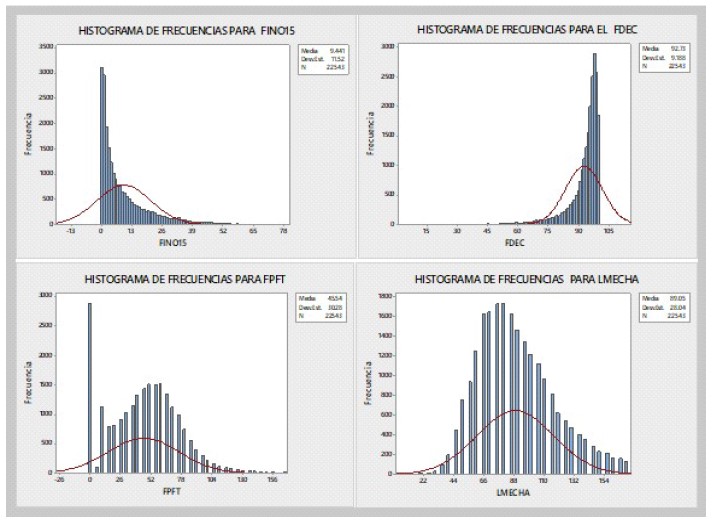
Figura 2 Histogramas de características físicas y textiles de la fibra de alpacas de la Región Puno, Perú: Porcentaje de fibras menores de 15 µm, Factor de confort, Finest point from the tip y Largo de Mecha
Existen exiguos referentes para determinar el número máximo de pares de datos y cómo es que este afecta sobre la significancia de r. Sin embargo, si se desea una estima muy precisa de la correlación en la población, será necesario siempre un número grande de sujetos (Morales y Rodríguez, 2016). El presente estudio utilizó un tamaño de muestra grande (n = 22 543), situación que se presenta como fortaleza en la precisión de sus resultados.
Por otro lado, es importante puntualizar que la validez del CCP se sustenta en el hecho de que la relación funcional entre variables es de tipo lineal (Restrepo y Gonzales, 2007). Consecuentemente, los CCP solo tienen sentido si la relación funcional es del tipo lineal. En casos que no fuera lineal, el CCP sólo indica ausencia de una relación lineal, más no la ausencia de algún otro tipo de relación; circunstancia que en ninguna de las referencias de investigación consideradas ha sido mencionado. En el presente estudio se evidencia que las relaciones funcionales entre dos variables distribuidas aproximadamente de manera normal no necesariamente grafican una función lineal. Paradójicamente algunas distribuciones no normales tienen una relación funcional de tipo lineal, circunstancias que requieren ser consideradas al momento de la interpretación del valor de CCP.
Un aspecto adicional que explica la razón de algunos valores elevados de CCP en el presente estudio y que contribuyen a generar diferencias, es el hecho de utilizar datos basados en medias (Triola, 2009). Las medias eliminan la variabilidad individual y pueden sobrevalorar el CCP. En este sentido, se asume que esto está ocurriendo en ciertas correlaciones del presente estudio, ya que usa medias de algunas variables como si fueran datos originales.
Significancia del Coeficiente de Correlación de Pearson
La significación estadística del CCP implica testar si r es estadísticamente diferente de cero (Díaz y Fernández, 2002), bajo el supuesto de la hipótesis Ho: ρ=0, a un nivel se significancia de α=0.05, siendo α la probabilidad de rechazar la Ho: ρ=0, que es verdadera.
El Cuadro 1 presenta valores-p (p-value) para los CCP. Se asumen valores de 0.000 excepto para las correlaciones CDV- FDEC (0.488) y CEM-PFPT (0.128); lo que implica que a la prueba de hipótesis se toma la decisión de aceptar la H1: ρ diferente de 0, infiriendo el hecho de que todas las correlaciones, excepto las dos mencionadas, muestran una relación funcional de variables de tipo lineal en diferente magnitud, aun para valores de r muy bajos (FDEH-LMECHA [0.041], FINO15-PFPT [0.068]), así como para valores muy elevados (DE-CEM [0.912], MDMF-FDEH [0.963]). Desde esta perspectiva, la mayoría de los r tuvo una significancia menor a 0.000, lo cual indica que entre variables existe una relación de asociación a un nivel de error de Tipo I <0.01; o que la Correlación es altamente significante diferente de cero. Sin embargo, es necesario precisar que, el valor de la significancia no considera la condición de la relación funcional entre variables.
En los cuadros 4 y 5 se observa que no es frecuente referir la significancia de los CCP. Aquellos que lo refieren hacen uso de asteriscos y NS para los casos en los que existe y no existe significación estadística, respectivamente; pero en ningún caso refieren el procedimiento del método para su determinación. Finalmente, muestras pequeñas con r grandes pueden no alcanzar significación o inversamente, muestras grandes con r pequeños pueden alcanzar significación estadística, aunque las diferencias biológicas sean irrelevantes; por lo que, es importante disponer de un número mínimo de individuos a estudiar para detectar como significativa una magnitud determinada (Díaz y Fernández, 2002), dado que de no hacerlo conlleva cometer Error de Tipo II.
Intervalos de Confianza para CCP.
La estimación del CCP por intervalos de confianza es un procedimiento alternativo en estadística aplicada, nunca referido en trabajos de investigación para caracteres en fibra de alpacas. Para ello se dispone de varios métodos (Pacheco y Correa, 2013), siendo el más conocido el propuesto por Fisher donde se realiza una transformación del CCP muestral (r), asumiendo su normalidad asintótica y se estima un intervalo para el CCP poblacional ρ (Krishnamoorthy y Xia, 2007). Sin embargo, la trasformación de Fisher es el menos eficiente para muestras de tamaño pequeño y r grandes, dado que en estas distribuciones el apuntamiento es ligeramente superior a cero (Sánchez y Borges del Rosal, 2004); de allí que es lógico esperar que z tiene una distribución aproximadamente Normal cuando el tamaño muestral es grande (Pacheco y Correa, 2013); circunstancia que abona a favor de la confiabilidad de los resultados obtenidos en el presente estudio, por la magnitud del tamaño de muestra utilizado.
En este contexto, y bajo la condición de que la transformación z de r no concuerde con la realidad teórica, los Intervalos de Confianza de los CCP determinados, entre las variables: DMF, DE, CRV, LMECHA, CDV y FDEH, pueden ser confiables debido a que sus distribuciones son aproximadamente normales y, consecuentemente, la transformación z de r con mayor razón será normal, condición que le da validez a dichos intervalos. Contrariamente, los intervalos de confianza para r entre las variables CEM, FINO15, FDEC y FPFT, no son confiables, por la violación de la razón explicada anteriormente.
El rango definido por los límites de confianza encontrados en el presente estudio, en términos absolutos, es más estrecha a medida que incrementa el valor de r, comportamiento concordante con lo expuesto por Pacheco y Correa (2013), lo que implica que los intervalos de confianza son de menor amplitud cuando el verdadero valor de r se acerca a 1.
Coeficiente de Correlación de Rangos Ordenados de Spearman (rs)
En el Cuadro 2 se observa que los CCS, en términos absolutos, se encuentran dentro del rango de 0.003 hasta 0.978, siempre precedidos de un signo, positivo o negativo, que definen la magnitud y sentido de la relación de asociación entre dos variables, respectivamente. Es una medida de asociación cuya relación funcional es de tipo lineal (Restrepo y Gonzales, 2007; Morales y Rodríguez, 2016. Según Mondragón (2014), el CCS examina la dirección y la magnitud de la asociación entre variables cuantitativas en cualquier tipo de asociación, no necesariamente lineal, que representa una ventaja comparativa respecto del CCP. Es necesario precisar que, la magnitud de la asociación obtenida no es el de los valores de las variables, sino el de las clasificaciones por rangos de dichos valores (Pérez, 2002), por lo que el CCS, procedimentalmente, es exactamente el mismo que el CCP, con la diferencia de que es calculado sobre rangos de observaciones (Camacho, 2008).
Se demostró que ninguna de las características en estudio tiene una distribución estrictamente normal (Cuadro 3). Esto implica que los CCP obtenidos tienen un sesgo que depende de cuan anormales son las distribuciones bivariadas, lo cual resta confiabilidad a los mismos; razón por la que el CCS resulta aplicable cuando no se cumplen los supuestos establecidos para el CCP (Artusi et al., 2002). Tiene la ventaja de ser una técnica no paramétrica de libre distribución probabilística, los supuestos son menos restrictivos y es robusto a la presencia de outliers (Restrepo y Gonzales, 2007). Por otro lado, el número de valores iguales en cada variable, como ocurre en el presente estudio, es grande, por lo que la ecuación definida para la determinación del CCS asume implícita- mente la corrección T por este efecto (Siegel y Castellán, 1998), circunstancias que le confieren mayor fiabilidad. Diversos investigadores señalan que a menos que sea excesivo el número de cantidades iguales, la corrección produce diferencias muy pequeñas en el valor de CCS (Barreto, 2011; Morales y Rodríguez, 2016).
Los valores de los CCP y CCS para las mismas variables (Cuadros 1 y 2) son diferentes. Es explicable que así ocurra por cuanto son producto de procedimientos diferentes que usan información diferente, aunque en esencia de una misma ecuación (Camacho, 2008). Ambos coeficientes guardan proporcionalidad en sus valores, en los que se observa que los CCP son relativamente mayores en mayor proporción.
No se registra información científica que determinen CCS cuantificando la magnitud de la relación de variables en características de la fibra en alpacas, así como la orientación de dichas relaciones por este parámetro, lo que inviabiliza contrastes y/o comparaciones, que redundarían en un mejor análisis de resultados. Circunstancia que plantea la disyuntiva ¿Cuál de los dos coeficientes es que mejor fiabilidad confiere al parámetro ρ? Una decisión técnica basado en teoría estadística orienta a que el CCS es el estadístico más adecuado que estima valores paramétricos de la relación de asociación entre variables vinculadas a las características físicas y textiles de la fibra de alpacas, en las condiciones establecidas en el presente estudio.
Significancia del Coeficiente de Correlación de Spearman
El Cuadro 2 presenta valores de probabilidad de la significancia para los CCS entre caracteres físicos y textiles de la fibra de alpacas de la Región Puno que prueba la hipótesis Ho: Rho=0, dado que la Ho: sea cierta. Se observa que el rango de dichos valores oscila entre 0.000 y 0.644. Muchos de dichos valores asumen valores de 0.000 excepto aquellos que corresponden a las correlaciones entre MDMF-LMECHA (0.644), CDV- FDEC (0.488) y CEM-PFPT (0.128). Se infiere que la mayoría de las correlaciones son significantes, excepto las tres citadas anteriormente, lo cual implica la existencia de una relación funcional lineal o cualquier otro tipo de función entre caracteres, en diferente magnitud y no debida al azar (Mondragón, 2014). Un comportamiento similar de estos valores es determinado para aquellos que definen la significancia del CCP; sin embargo, los de Spearman son más confiables, debido a la observancia de requerimientos procedimentales para su determinación. No se dispone de referentes científicos que den testimonio del significado y la implicancia de este parámetro, al tiempo que permita ejecutar contrastes.
Intervalos de Confianza para los CCS
Es ostensible que no es práctica común determinar coeficientes de correlación a través de intervalos de confianza. Probar un parámetro de correlación igual a cero no siempre es de interés, consecuentemente un intervalo de confianza puede ser más informativo (Gardner y Altman, 1986; Schmidt, 1996). Los intervalos de confianza en este estudio son diferentes, tanto para los de Pearson y de Spearman. Se evidencia proporcionalidad para cada uno de los coeficientes obtenidos por ambos procedimientos, respectivamente. Es manifiesto que los determinados para el CCS definen intervalos relativamente más estrechos, cuya diferencia promedio fue de 0.020026 que los de Pearson (0.020092), para el mismo tamaño de muestra y nivel de confianza del 95%.
No se dispone de información científica acerca de la estima de CCS por intervalos de confianza en caracteres de fibra de alpacas para caracteres objeto de estudio del presente, que permita el contraste e inferencias.
Por último, los CCP son determinados como complemento en trabajos de investigación de nivel descriptivo, eludiendo la importancia implícita que éstos representan en investigación científica de nivel relacional; a pesar de que el uso del coeficiente de correlación de Pearson es extensísimo, también lo son las incorrecciones y omisiones al momento de emplearlos, las imprecisiones cuando de verificar sus supuestos se trata, o incluso, la confusión y desinformación a la hora de interpretar los resultados (Kozak et al., 2012).
CONCLUSIONES
Se determinaron coeficientes de correlación de Pearson y Spearman para pares de caracteres físicos y textiles de la fibra de alpacas que definen el sentido y la magnitud, así como la significancia de la relación funcional lineal entre caracteres. Estos asumen valores muy discrepantes para la misma relación de variables respecto de otros estudios.
Los valores de los límites de confianza definen el intervalo dentro del cual se encuentran los parámetros de los coeficientes de correlación con un determinado nivel de confianza. Estimados de los coeficientes de correlación por intervalos de confianza no es reportada en estudios sobre caracteres objeto de estudio del presente.
El mejor procedimiento estadístico que define la relación de asociación lineal entre características físicas y textiles de la fibra de alpacas es el coeficiente de correlación de Spearman, debido a que las características de sus variables, en varios aspectos, así como sus distribuciones conjuntas son menos restrictivos que los del coeficiente de correlación de Pearson. Paradójicamente nunca referido en trabajos de investigación en este contexto.
Las correlaciones, especialmente la de Pearson, se determinan como complemento en trabajos de investigación de nivel descriptivo, escasamente referidos en investigaciones de nivel relacional.












 uBio
uBio 


