INTRODUCCIÓN
La resistencia a los antimicrobianos (AMR, del término en inglés antimicrobial resistance) es un problema grave y global, siendo declarado por la Organización Mundial de la Salud (OMS) como uno de los 10 problemas que amenazan la salud pública mundial (Rodríguez-Gascón et al., 2021). Murray et al. (2022), en su estudio estimaron cerca de 5 millones de muertes por año asociadas con AMR en 2019 en el mundo y 1.27 millones asociadas con infección bacteriana. La OMS estima que para 2050 las muertes aumentarán a 10 millones de personas por año (Mi et al., 2022).
A causa de la AMR, los medicamentos se vuelven ineficaces y las infecciones persisten en el cuerpo, lo que aumenta la morbilidad, la mortalidad y el riesgo de propagar infecciones. Además, existe un impacto económico significativo que dificulta la capacidad de tratar enfermedades infecciosas e impide avances en el campo de la medicina (Zhu et al., 2022). La selección de microorganismos resistentes aumenta con el uso innecesario e indiscriminado de antimicrobianos, uso de antimicrobianos de amplio espectro, sub-dosificaciones y terapias con duración inadecuada (Guardabassi et al., 2018). Por lo tanto, dosificar con precisión un tratamiento antimicrobiano es crucial para aumentar la eficacia terapéutica, disminuir el riesgo de inducir AMR y afectar la microbiota del huésped (Rawson et al., 2021).
La Medicina Veterinaria también contribuye a la propagación de la AMR, lo que conlleva importantes costos para la salud y la economía de la población (Innes et al., 2020). Souza et al. (2020) aislaron bacterias de infecciones en pequeños animales de Paraná, Brasil, encontrando 64.3% (151/235) de aislados clasificados como multirresistentes y 15.3% como extensivamente resistentes, demostrando el aumento en el número de agentes multirresistentes entre los animales domésticos. Esto representa un riesgo para todos aquellos que entran en contacto directo o indirecto con animales infectados o portadores, incluso a través del entorno (Souza et al., 2020). Es así que la European Medicines Agency (EMA) desarrolló lineamientos (EMA, 2016a) para regular el registro de medicamentos veterinarios, el cual también se utiliza como base para optimizar las dosis de medicamentos veterinarios disponibles en el mercado (Guardabassi et al., 2018).
La optimización de los protocolos terapéuticos antimicrobianos, según lo propuesto en el cuarto objetivo del Plan deAcción Mundial sobre la resistencia a los antimicrobiana de la OMS (WHO, 2015), puede llevarse a cabo mediante el modelado farmacocinético/ farmacodinámico (PK/PD). Este enfoque ya se ha utilizado para el desarrollo de fármacos, con el fin de seleccionar para estudios clínicos los regímenes de dosificación apropiados (dosis, intervalo y frecuencia de administración) con potencial efectividad (Jorda y Zeitlinger, 2020; Toutain et al., 2021).
Este abordaje ya se ha llevado a cabo en Medicina Veterinaria como una estrategia para optimizar los regímenes de dosificación de los medicamentos en el mercado. Como ejemplo, se tiene el estudio de Ferrante (2018) evaluar la eficacia de un régimen de dosificación de florfenicol contra Mannheimia haemolytica y Pasteurella multocida en llamas y posteriormente en alpacas (Ferrante y Wosiacki, 2019). Otros ejemplos incluyen los trabajos de Lees et al. (2015) con amoxicilina contra Mannheimia haemolytica y Pasteurella multocida en terneros, y por Dorey et al. (2017) con florfenicol contra Actinobacillus pleuropneumoniae y Pasteurella multocida en cerdos. El objetivo de esta revisión fue abordar los aspectos metodológicos del proceso de optimización de dosis de antibióticos.
Conceptos Iniciales
La farmacocinética estudia los procesos de absorción, distribución, biotransformación y eliminación (ADME) de los fármacos. En términos generales, representa lo que el cuerpo hace con la droga. Por otro lado, la farmacodinámica estudia el efecto farmacológico/toxicológico; es decir, lo que la droga le hace al organismo (Fan y de Lannoy, 2014; Roberts et al., 2016). El conocimiento del comportamiento del fármaco en el organismo es esencial para definir un régimen de dosificación racional, ya sea para su empleo en estudios clínicos de eficacia y toxicidad o para optimizar los regímenes utilizados de forma rutinaria (Cavalheiro y Comarella, 2016).
La farmacometría es definida por la Food and Drug Administration (FDA) de los Estados Unidos como «la ciencia que cuantifica la información sobre medicamentos, enfermedades y ensayos para ayudar en el desarrollo de medicamentos eficaces y/o decisiones regulatorias» (Zhu, 2021). Utiliza modelos matemáticos de fisiología, farmacología y enfermedades para describir y cuantificar las interacciones fármaco-paciente; es decir, utiliza modelos farmaco-cinéticos (PK), farmacodinámicos (PD), de exposición-respuesta (modelos PK/PD) y de progresión de la enfermedad (Janssen et al., 2022).
Modelos Matemáticos
Debido a los avances tecnológicos tales como la mayor digitalización de datos en hospitales y clínicas, la calidad de los datos recolectados, los exámenes de laboratorio realizados y la estandarización de procedimientos, entre otros, se dispone de bases de datos muy robustas. Como resultado, existe una mayor atención sobre la oportunidad de aplicar el machine learning y la inteligencia artificial como una innovación en el campo de la farmacometría, con el fin de integrarlos en el modelado y la simulación (Chaturvedula et al., 2019; McComb et al., 2022).
Los modelos matemáticos son representaciones de un sistema que utilizan ideas y lenguaje matemáticos para producir una descripción aproximada del sistema real. A partir del modelo es posible realizar simulaciones con el fin de predecir el comportamiento del sistema bajo ciertas condiciones (Hasan et al., 2022). En el campo de la farmacología, el sistema representado es el organismo animal; así, el modelo permite describir y comprender el tiempo de exposición a un fármaco y la respuesta farmacológica tras la administración de diferentes dosis o formulaciones de un fármaco (Mould y Upton, 2012). Se han utilizado modelos matemáticos en el proceso de desarrollo de nuevos fármacos y en la predicción de la toxicidad inducida por fármacos (Mody et al., 2020).
Modelo farmacocinético (PK)
Existen dos enfoques utilizados para el entendimiento de la farmacocinética de un fármaco: el análisis PK no compartimental (NCA) y el análisis PK compartimental.
NCA es independiente del modelo, y reside en ecuaciones algebraicas que se usan para estimar los parámetros PK, permitiendo que el análisis sea menos complejo, más rápido y económico que los métodos compartimentales (Allucent, 2021). Los principales parámetros farmacocinéticos son el área bajo la curva (ABC), la vida media (T½), la concentración máxima (Cmax), el tiempo para alcanzar la concentración máxima (Tmax), el volumen de distribución (Vd) y el Clearance (Cl) (PKanalix, 2023).
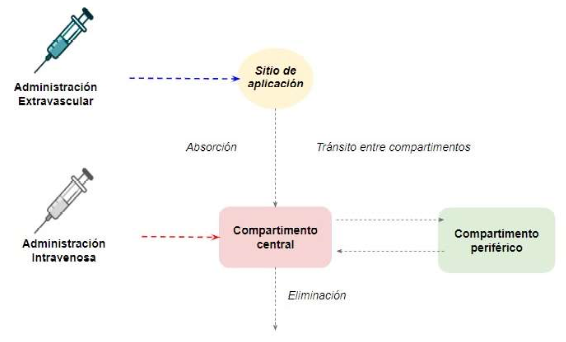
Los modelos farmacocinéticos describen la relación entre el fármaco administrado y su concentración a lo largo del tiempo en el organismo. El modelo PK tiene como objetivo describir los procesos farmacocinéticos de absorción, distribución, metabolismo y eliminación de fármacos (Mould y Upton, 2012). Así, en el análisis PK compartimental, el organismo se representa como un sistema de uno o más compartimentos, que no representan los mecanismos anatómicos y fisiológicos (Mi et al., 2022). Los modelos pueden ser de un solo compartimento o bicompartimental (Figura 1), que incluye el compartimento central (tejidos más vascularizados, como el corazón, riñones y cerebro) y un compartimento periférico o multicompartimental (Hang et al., 2016). Solo los modelos farmacocinéticos basados en fisiología (PBPK) describen el proceso ADME basado en mecanismos fisiológicos, bioquímicos y fisicoquímicos, permitiendo simular la concentración de fármacos en diversos tejidos y fluidos corporales, en diferentes escenarios biológicos (Lin et al., 2016).
Como se ejemplifica en el modelo anterior, los principales parámetros farmacocinéticos de los modelos compartimentales son la constante de absorción (Ka), que describe la velocidad a la que se absorbe el fármaco desde el sitio de aplicación hacia la sangre; el volumen de distribución (Vd), que representa la distribución del fármaco inicialmente en un compartimento central y, posteriormente, en compartimentos periféricos; y Clearance (Cl), que representa la eliminación del fármaco (Fan y de Lannoy, 2014).
Los modelos farmacocinéticos compartimentales pueden utilizarse para evaluar el comportamiento de los más diversos tipos de fármacos y en una amplia variedad de especies, como se evidencia en el trabajo de Tameirão et al. (2022) con florfenicol en tilapia (Oreochromis niloticus) sometida a diferentes temperaturas, y por Grabowski et al. (2018) quienes evaluaron el impacto de la producción de leche en la farmacocinética de diferentes fármacos.
Modelos farmacocinéticos poblacionales (popPK)
Los modelos farmacocinéticos poblacionales estudian la farmacocinética a nivel poblacional, a fin de entender y analizar el impacto de covariables como edad, sexo, raza y condición corporal, entre otras, sobre la farmacocinética y, en consecuencia, sobre la farmacodinámica (FDA, 2022). Así, en el estudio de Tameirão et al. (2022) se determinó el efecto de la temperatura de crianza sobre la farmacocinética del florfenicol en tilapias (O. niloticus), demostrando que la constante de absorción y el Clearance eran menores a temperaturas más bajas, probablemente asociado con una disminución en el metabolismo del animal a temperaturas más bajas.
La variabilidad farmacocinética se define como fija cuando las causas de la variabilidad son medibles y predecibles o residual cuando las causas de la variabilidad no se pueden identificar definitivamente (Rawson et al., 2021). La variabilidad puede ser interindividual, estando asociada, por ejemplo, a la edad, raza, obesidad, medicamentos, comorbilidades, entre otras, o intraindividual, asociada al desequilibrio hídrico, disfunción renal o hepática, entre otros (Mould y Upton, 2013).
Los datos recopilados de individuos en una población determinada pueden evaluarse en forma simultánea mediante un modelo de efectos mixtos no lineales (NLMEM). Esta herramienta permite cuantificar la variabilidad en la disposición y respuesta farmacológica según las características de los individuos de la población (Bon et al., 2018). El término «no lineal» se refiere al hecho de que la variable dependiente (p. ej., la concentración) está relacionada de forma no lineal con los parámetros del modelo y con las variables independientes. Los «efectos mixtos» se refieren a la parametrización, los parámetros que no varían entre individuos se denominan «efectos fijos» y los parámetros que varían entre individuos se denominan «efectos aleatorios» (Mould y Upton, 2013).
Los modelos PopPK están compuestos por datos, modelo estructural (describe la concentración x tiempo), modelo estadístico (describe la variabilidad residual), modelo de covariables y el software responsable del modelado (Mould y Upton, 2013; Bon et al., 2018). En general, la estructura del modelo se puede representar mediante el esquema indicado en la Figura 2.
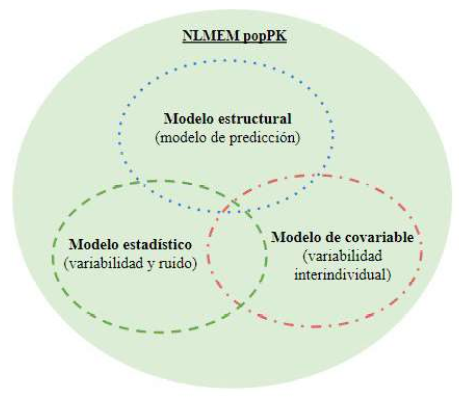
Fuente: Adaptado de Bon et al. (2018)
Figura 2. Estructura del modelo farmacocinético poblacional (popPK). NLEM: Modelo de efectos mixtos no lineales; popPK: Modelo farmacocinético poblacional.
Modelo farmacodinámico (PD)
Los modelos farmacodinámicos describen la relación entre la exposición al fármaco y la respuesta; es decir, el efecto farmacológico que proporciona información más sólida sobre la acción del fármaco. Esto permite estudiar los aspectos fisiológicos y bioquímicos de fármacos, así como los agentes patológicos en el organismo (Nielsen y Friberg, 2013). Los parámetros de los modelos farmacodinámicos representan la relación exposición-efecto, por lo que están asociados con el tiempo de aparición del efecto (p. ej., inmediato o retardado), si la acción es de inhibición o estimulación y el comportamiento de la relación concentración-efecto (sigmoide, lineal o de máximo efecto) (Upton y Mould, 2014).
Ejemplos de documentos que abordan el modelado farmacodinámico incluyen el de Gonzaga et al. (2021), que evalúa el efecto de diferentes dosis de detomidina en caballos; el de Gaddini et al. (2022), que verifica el efecto sedativo y los cambios fisiológicos en caballos sometidos a la administración intramuscular de detomidina y morfina; y el de Ferrante et al. (2018) que simula el efecto sedativo de altas dosis de detomidina en caballos.
Al igual que los modelos PK, los modelos PD también se analizan a nivel poblacional usando el enfoque NLMEM, teniendo una estructura similar a la representada en la Figura 2. La variabilidad en la farmacodinámica puede estar asociada con la respuesta inmune del huésped, el tamaño del inóculo, el sitio de infección, la formación de biopelículas, la concentración mínima inhibitoria (CIM) del organismo, la resistencia antimicrobiana, la penetración de fármacos, y el efecto pos-antibiótico, entre otros (Rawson et al., 2021).
Enfoque traslacional y traslacional inverso
Se utilizan modelos animales en el proceso de descubrimiento y desarrollo de fármacos para caracterizar la fisiopatología de la enfermedad, evaluar el mecanismo de acción de los fármacos y establecer relaciones farmacocinéticas / farmacodinámicas, todo esto con el fin de estimar regímenes de dosificación clínica y determinar márgenes de seguridad y toxicidad (McGonigle y Ruggeri, 2014). Los resultados obtenidos en estudios preclínicos en animales se extrapolan luego a humanos, siendo este enfoque conocido como traslacional (Bhagunde et al., 2019; Scheetz et al., 2021). Sin embargo, como alternativa en las primeras etapas de investigación y desarrollo de fármacos, se propuso la ciencia traslacional inversa, cuyo objetivo es aprovechar la información disponible de humanos y animales que comparten enfermedades similares para desarrollar mejores predicciones y terapias en medicina veterinaria (Figura 3) (Kasicha-yanula y Venkatakrishnan, 2018; Schneider et al., 2018).
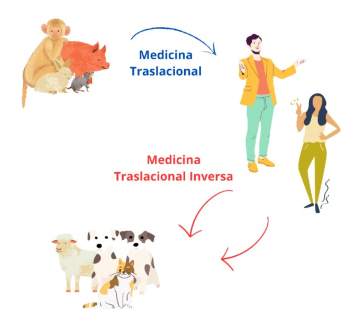
Fuente: Adaptado de Schneider et al. (2018)
Figura 3. Esquema de medicina traslacional y medicina traslacional inversa.
Con base en esta metodología, el equipo de investigación construyó un modelo de cloxacilina sódica en cabras mediante la integración de modelos farmacocinéticos de cloxacilina sódica en ovejas y cabras (Figura 4).
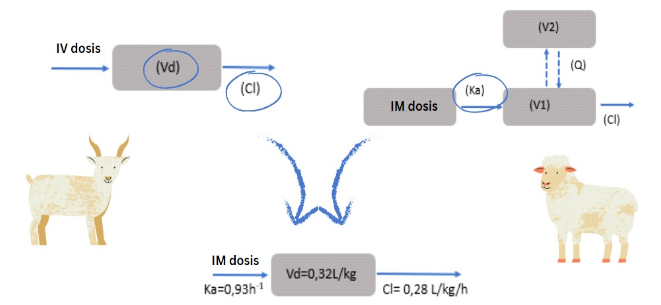
Fuente: Felix et al. (2023)
Figura 4. Representación esquemática de los modelos farmacocinéticos de la cloxacilina sódica. Leyenda: IV -Intravenosa; Vd -Volumen de distribución; Cl -Liquidación; Ka Constante de absorción; V1 -Volumen del compartimento central (la mayoría de los órganos vascularizados); V2 -Volumen del compartimento periférico; Q -Tránsito entre compartimentos; IM - Intramuscular.
Para ello, los datos de la constante de absorción obtenidos del modelo ovino se integraron con el volumen de distribución (Vd) y aclaramiento (Cl) del modelo caprino, como se observa en el esquema de la figura (Felix et al., 2023).
Modelos farmacocinéticos/farmacodinámicos (PK/PD)
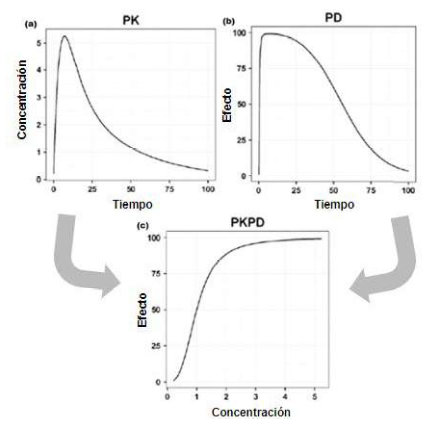
Los modelos PK/PD permiten describir la relación entre la concentración del fármaco y el efecto farmacológico, con el fin de evaluar la variación del efecto farmacológico en función de la variación de la concentración del fármaco (Mould y Upton, 2012). El modelado farmacocinético / farmacodinámico (PK/PD) ha sido una herramienta ampliamente utilizada en la selección y optimización de los regímenes de dosificación, en particular para los antimicrobianos (Toutain et al., 2021). Este enfoque se discute más adelante. En la Figura 5 se muestra una representación gráfica de los perfiles de concentración-tiempo (modelos PK), efecto-tiempo (modelo PD) y concentración-efecto (modelo PK/PD).
Fuente: Adaptado de Rawson et al. (2021)
Figura 5. Relación entre modelos farmacocinéticos (PK) y farmacodinámicos (PD). Título: a. Modelo farmacocinético (PK) perfil de concentración en función del tiempo; b. Modelo farmacodinámico (PD) - efecto en función del tiempo; c. Modelo farmacocinético/farmacodinámico (PK/PD): perfil de efectos en función de la concentración.
Integración Farmacocinética / Farmacodinámica para Optimizar el Régimen de Dosificación de Antimicrobianos
La optimización del uso de antimicrobianos en animales y humanos está en el punto de mira debido a la preocupación mundial sobre la resistencia a los antibacterianos, uno de los 10 principales problemas mundiales que amenazan la salud pública. En 2015, la Organización Mundial de la Salud (OMS) estableció un Plan de Acción Mundial sobre la Resistencia a los Antimicrobianos, siendo la optimización una de las estrategias prioritarias (WHO, 2015; Zhu et al., 2022).
El documento Guideline on the use of pharmacokinetics and pharmacodynamics in the development of antimicrobial medicinal products (EMA/CHMP/594085/2015) de la EMA (2016b) establece el uso de la integración PK/PD para determinar regímenes de dosis con mayor potencial de eficacia terapéutica. Además, orienta los puntos a considerar para determinar un régimen de dosis adecuado. La optimización se basa en el conocimiento de la relación antimicrobiano y agente, para integrar la concentración mínima inhibitoria (CIM) y los índices PK/PD en las simulaciones in silico, utilizando simulaciones de Monte Carlo para determinar la probabilidad de alcanzar el objetivo, estableciendo si el régimen es eficaz.
Los puntos por considerar para determinar/optimizar los regímenes de dosificación son (EMA, 2016b):
Aspectos microbiológicos: distribución de la población de CIM y curva de muerte bacteriana, que apoyará el conocimiento de la relación entre exposición y efecto antimicrobiano;
Determinación del índice PK/PD y su magnitud a partir de estudios no clínicos o de estudios de curvas de muerte bacteriana;
Datos farmacocinéticos de la población diana (estudios clínicos);
Determinación de la probabilidad de alcanzar el objetivo (PTA) a partir de simulaciones;
Evaluación de las relaciones clínicas de exposición-respuesta (E-R) utilizando datos que se recopilan durante los estudios clínicos que evalúan los resultados clínicos y microbiológicos en los pacientes.
Índices farmacocinéticos farmacodinámicos (PK/PD)
Los fármacos pasan por procesos farmacocinéticos (absorción, distribución, metabolización y excreción -ADME) desde su ingreso al organismo, influenciando su concentración en plasma y tejidos y, en consecuencia, en su efecto. En el caso de los antibióticos, estos son capaces de promover un efecto bactericida o bacteriostático sobre el microorganismo al llegar al sitio de acción en la concentración adecuada (Asín-Prieto et al., 2015).
La Concentración Inhibitoria Mínima (CIM) es el mayor indicador del efecto de un antimicrobiano, ya que informa la susceptibilidad del patógeno a un determinado antibiótico (Nielsen et al., 2011). La CIM puede determinarse por microdilución en placa, macrodilución en tubo o E-test, y debe seguirse los estándares establecidos por el Clinical Laboratory Standards Institute CLSI (CLSI, 2024) o European Committee on Antimicrobial Susceptibility Testing (EUCAST, 2024a, 2024b) (CLSI, 2018).
La CIM utilizada es representativa de varios aislamientos de la misma especie, por lo que para cada aislado se determina la CIM, obteniendo una distribución poblacional. Siempre se debe describir la metodología utilizada para realizar el CIM (EMA, 2016b). A partir de la distribución de las CIM se puede calcular la CIM50 y la CIM90, que representan los valores de la CIM donde se inhibe el 50 y 90% de la población de aislados, respectivamente. Sin embargo, CIM50 y CIM90 no son capaces de diferenciar las cepas wild type (cepas silvestres) de las cepas con un mecanismo de resistencia adquirido (Turnidge et al., 2006). Las European Committee on Antimicrobial Susceptibility Testing (EUCAST) define las cepas wild type como aquellas especies que no muestran un mecanismo de resistencia adquirida fenotípicamente detectable al agente antimicrobiano en cuestión (EUCAST, 2016).
Una alternativa para determinar el valor de la CIM que cubre solo las cepas wild type es calcular el punto de corte epidemiológico (ECOFF). CLSI proporciona el software ECOFFinder (ECOFFinder v. XL 2010 v2.1; https://clsi.org/meetings/microbiology/ecoffinder/), programa basado en la metodología descrita por Turnidge et al. (2006), que permite analizar la distribución poblacional de CIM y estimar una población wild type y el punto de corte epidemiológico. En Medicina Veterinaria se han realizado estudios con esta metodología para optimizar la dosis de florfenicol frente a Piscirickettsia salmonis en salmón (San Martín et al., 2019) y de oxitetraciclina frente a Mannheimia haemolytica y Pasteurella multocida aisladas de terneros (Lees et al., 2018).
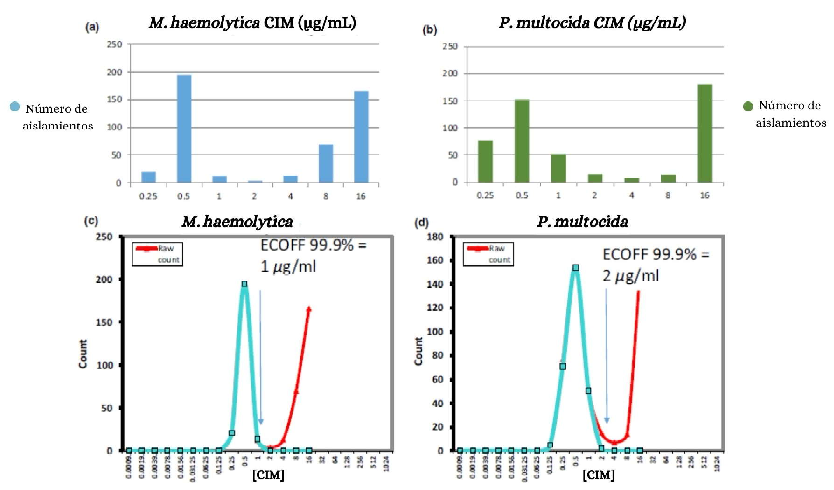
La Figura 6 muestra la distribución de la CIM y la determinación del Punto de Corte (Cutoff) Epidemiológico (ECOFF) para los aislamientos de M. haemolytica y P. multocida. Se tiene que para ambos aislamientos existen dos distribuciones de CIM. Así, para M. haemolytica se tiene una primera distribución que va de 0.25 a 2 µg/mL, y una segunda en 4 µg/mL, lo que puede sugerir cepas con cierta resistencia. Por lo tanto, ECOFF permite separar estas cepas y establecer un punto de corte basado en las cepas de tipo silvestre presentes en la primera distribución. Por lo tanto, en ese caso, el ECOFF de oxitetraciclina para M. haemolytica fue de 1 µg/mL.
Fuente: Adaptado de Lees et al. (2018)
Figura 6. Distribución de la Concentración Inhibitoria Mínima (CIM) y determinación del Punto de Corte Epidemiológico (ECOFF) para los aislamientos de M. haemolytica y P. multocida. Leyenda: Distribuciones de CIM para P. multocida (498 cepas, a) y M. haemolytica (481 cepas, b). La determinación de las cepas de wild type se determinó estadísticamente según Turnidge et al. (2006) para calcular el percentil 99.9 del ECOFF. Las distribuciones de wild type para P. multocida (c) y M. haemolytica (d) se ajustaron con una curva azul.
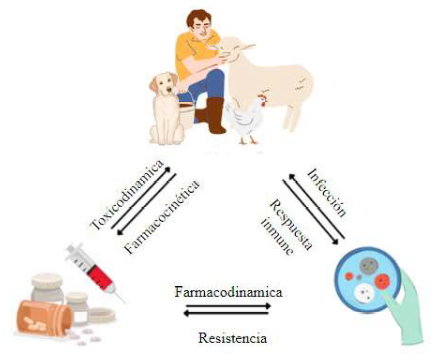
Se sabe que la CIM por sí sola no es capaz de reflejar la interacción entre patógeno, huésped y antimicrobiano, factores que también condicionan la respuesta clínica. Sin embargo, el análisis de la relación PK/PD de los antimicrobianos permite integrar las propiedades PK y PD para optimizar la terapia antimicrobiana (Figura 7) (Landersdorfer y Nation, 2021; Rodríguez-Gascón et al., 2021).
Fuente: Adaptado de Asín-Prieto et al. (2015)
Figura 7. Factores relacionados con la eficacia antimicrobiana: microorganismo, huésped y antimicrobiano.
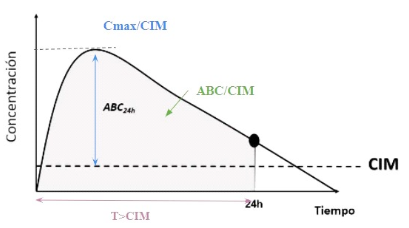
Las relaciones de exposición antimicrobiana al microorganismo se estudian a partir de modelos PK/PD. Estos modelos pueden ser in vitro, ex vivo y/o in vivo, considerándose metodologías complementarias (Luo et al., 2019; Rodríguez-Gascón et al., 2021). La agencia reguladora EMA ha establecido pautas para garantizar la calidad de los medicamentos antimicrobianos (EMA, 2016a, 2016b, 2022). Las relaciones PK/PD de los antimicrobianos se pueden clasificar en tres índices PK/PD, que predicen la eficacia clínica, que fueron estandarizados por Mouton et al. (2005) como: tiempo que la concentración del fármaco estuvo por encima de la CIM (T>CIM), concentración máxima dividida por CIM (Cmax/CIM) y área bajo la curva de concentración-tiempo dividida por CIM (ABC/CIM) (Nielsen y Friberg, 2013). La relación PK/PD de los antimicrobianos se muestra en la Figura 8.
Fuente: Adaptado de Asín-Prieto et al. (2015) y Papich (2014)
Figura 8. Representación de los índices farmacocinéticos / farmacodinámicos (PK/ PD) asociados a la eficacia de los antimicrobianos in vivo. Leyenda: CIM. Concentración inhibitoria mínima; ABC. Área bajo la curva; Cmax. Concentración máxima de fármaco en plasma; T>CIM. Tiempo en que la concentración del fármaco estuvo por encima de la CIM; ABC/CIM. Área bajo la curva de concentración-tiempo durante 24 horas dividida por la CIM; Cmax/CIM. Concentración máxima dividida por CIM. Si no está presente un subíndice que indique otro periodo de tiempo, se supone que el ABC es de 24 h.
Para determinar el índice PK/PD más adecuado es necesario realizar un ensayo de curva de muerte en caldo Muller-Hinton o plasma/suero, leche, entre otros, dependiendo del agente a estudiar (Zhang et al., 2022). Así, el efecto del antibiótico (reducción del conteo bacteriano, expresado en unidades formadoras de colonias - UFC) es evaluado por un modelo matemático a través de la ecuación de Hill, describiendo un modelo Sigmoid Emax (Ecuación 1:E=E0 + (Emax*XN)/ECN 50+ XN), durante 24 horas de tratamiento (Lees, et al., 2004; Mouton et al., 2012).
En la ecuación, E0 es el crecimiento bacteriano después de 24 h de incubación en ausencia de antibiótico sustraído del inóculo inicial, y se expresa como log10 UFC/mL; Emax es la inhibición máxima del crecimiento bacteriano, determinada como el cambio desde el recuento inicial en log10 CFU/mL en 24 h de incubación con el fármaco; X es la variable independiente (el índice PK/PD), y N es el coeficiente de Hill, que describe la pendiente de la curva; EC50 es el valor del índice PK/PD que produce el 50% del efecto antibacteriano máximo (Lees et al., 2015). Se debe aplicar el coeficiente de regresión (R2) para evaluar la relación entre los parámetros PK/PD y el efecto antibacteriano (Figura 9); de modo que cuanto mayor sea el valor de R2, más correlacionado estará el efecto con los parámetros PK/PD (Zhang et al., 2022).
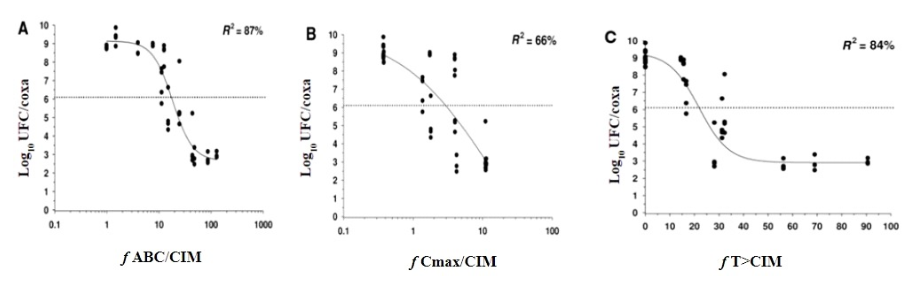
Fuente: Adaptado de Dudhani et al. (2010)
Figura 9. Representación del cociente colistina y P. aeruginosa para cada uno de los índices PK/PD. Leyenda: Las líneas representan el ajuste de las funciones sigmoideas Emax para cada uno de los índices PK/PD: A) ABC. Área bajo la curva de concentración-tiempo dividida por la concentración inhibitoria mínima (CIM), B) Cmax/CIM. Concentración máxima dividida por CIM y C) T>CIM Tiempo en que la concentración del fármaco estuvo por encima de CIM; f. fracción libre. Para cada uno de los índices PK/PD, se presentó el coeficiente de regresión (R2).
Cuando se estima el índice PK/PD en medios donde no se considera la unión a proteínas plasmáticas, como en ensayos in vitro con caldo Muller-Hinton, el fármaco estará totalmente libre en el medio. Esto es importante porque solo la fracción libre (f) realiza la acción. Por lo tanto, los índices PK/PD que no consideran la fracción libre pueden sobrestimar la exposición del microorganismo al antimicrobiano. Así, estos índices a menudo se representan de la siguiente manera: fT>CIM, fCmax/CIM o fABC/CIM (Papich, 2014).
Una vez conocido el patrón de actividad del fármaco a través de la ecuación de Hill, se debe establecer la magnitud del índice PK/PD necesario para que tenga un efecto antibacteriano. Así, el objetivo farmacodinámico (pharmacodynamic target -PDT) corresponde a un valor numérico, de magnitud, en el que se alcanzan los niveles deseables de respuesta prevista. Esto, a su vez, se puede cuantificar en tres niveles de inhibición del crecimiento: acción bacteriostática, acción bactericida y erradicación bacteriana (Figura 10). Los valores para acciones bacteriostáticas, bactericidas y de erradicación se definen como aquellos valores que producen E = 0 (ningún cambio en el recuento bacteriano después de 24 h de incubación), E = 3 (reducción de 3 log o 99.9% del recuento bacteriano). contar el inóculo inicial después de 24 h de incubación) y E = 4 (una reducción de 4 log o 9.99 % del recuento bacteriano del inóculo inicial) (Nielsen y Friberg, 2013).
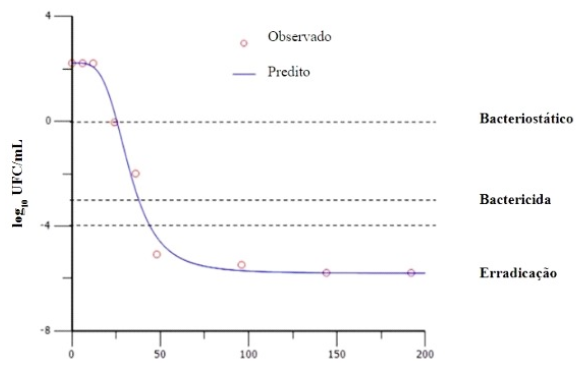
Fuente: Adaptado de Dorey et al. (2017)
Figura 10. Gráfico de muestra de ABC24h/ CIM frente al cambio en el recuento bacteriano desde el inicio (log10 CFU/mL). Leyenda: ABC24h/CIM. Área bajo la curva de 24 horas dividida por la concentración inhibitoria mínima.
Se han realizado diversos estudios para determinar las relaciones PK/PD para diferentes clases de antibióticos. La eficacia de los antibióticos dependientes del tiempo (T>CIM) depende de la concentración del fármaco que permanece por encima de la CIM durante un tiempo determinado entre intervalos de administración, siendo los betalactámicos los principales representantes de este grupo. Para la eficacia dependiente de la concentración (Cmax/CIM), la eficacia está relacionada con cómo el fármaco alcanza una concentración muy alta. Estos se encuentran representados por los aminoglucósidos y las quinolonas. También existen antibióticos dependientes del tiempo y de la concentración (ABC/CIM), como las tetraciclinas y los macrólidos (Asín-Prieto et al., 2015; Rodríguez-Gascón et al., 2021).
Aunque se han determinado índices PK/ PD para clases de antibióticos, algunos autores han demostrado que estos índices pueden variar dentro de las clases, según el agente y la forma en que se determina. Esto se demostró en el estudio de Lees et al. (2015), quienes evaluaron la curva de muerte bacteriana de Mannheimia haemolytica y Pasteurella multocida frente a amoxicilina en dos medios (caldo Mueller-Hinton y suero de ternera). En ese estudio, M. haemolytica mostró un comportamiento dependiente de la concentración en ambos medios, así como P. multocida en suero, contrario a lo ya descrito por Craig (2003), quien clasificó a las penicilinas en general como dependientes del tiempo. Así, debido al comportamiento codependiente frente a la amoxicilina, para estas especies el índice PK/PD más adecuado para predecir la eficacia pasa a ser el ABC/CIM (Nielsen y Friberg, 2013).
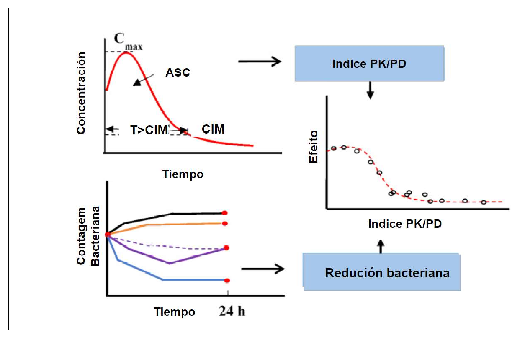
Fuente: Adaptado de Mi et al. (2018)
Figura 11. Diagrama de los pasos para la determinación del índice PK/PD.
Los datos de la PDT no siempre están disponibles en Medicina Veterinaria, por lo que el valor de la PDT puede extrapolarse a partir de estudios en humanos. Esto es válido porque la PDT no depende de las características del animal y tiene una validez genérica entre las especies animales ya que depende principalmente de la interacción del fármaco con la bacteria (Toutain et al., 2021). Sin embargo, se necesitan datos farmacocinéticos de la especie animal en cuestión para definir las dosis necesarias para alcanzar el PDT (Toutain et al., 2021).
Con el PDT establecido, es posible determinar la probabilidad de que una determinada población alcance el PDT. La probabilidad de que se logre un valor específico del índice PK/PD asociado con la efectividad del antibiótico en una CIM determinada se define como la probabilidad de alcanzar el objetivo (PTA) (Rodríguez-Gascón et al. 2021). El PTA se determina a partir de simulaciones, siendo más confiable cuando se toman en cuenta las variaciones inter e intraindividuales. La simulación de Monte Carlo es una herramienta de modelado estadístico avanzado que le permite expandir el tamaño de la muestra al considerar la variabilidad de los parámetros farmacocinéticos al estimar los índices PK/PD para proporcionar predicciones del resultado de diferentes enfoques terapéuticos o determinación de PTA. El PTA corresponde al porcentaje de pacientes simulados con un índice PK/PD estimado igual o mayor al PDT Roberts et al., 2011; Asín-Prieto et al., 2015). Una representación gráfica se puede ver en la Figura 12. Los regímenes de dosificación potencialmente efectivos deben proporcionar un PTA e» 90% (EMA, 2016b).
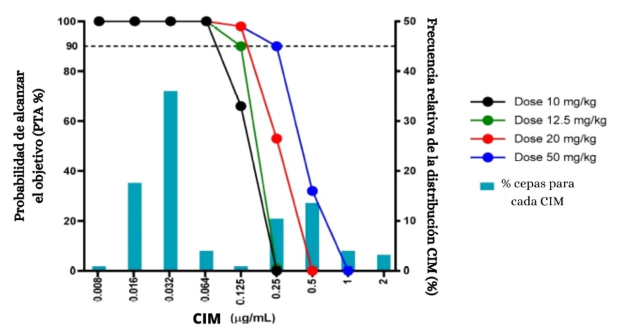
Fuente: Adaptado de Temmerman et al. (2021)
Figura 12. Representación gráfica de la probabilidad de alcanzar el objetivo (PTA). Leyenda: Probabilidad de alcanzar el objetivo (PTA) para varios regímenes de dosificación de enrofloxacina. El objetivo PK/PD era fABC/CIM e» 100.
Consideraciones Finales
La integración farmacocinética / farmacodinámica es una excelente herramienta para optimizar la determinación del régimen de dosis de antimicrobianos. Esta estrategia se puede utilizar para medicamentos disponibles en el mercado, con el fin de actualizar los prospectos, lo que lleva a regímenes más efectivos y a una disminución en la aparición de resistencia a los antimicrobianos.












 uBio
uBio