Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Peruana de Medicina Experimental y Salud Pública
versión impresa ISSN 1726-4634
Rev. perú. med. exp. salud publica vol.33 no.1 Lima ene./mar. 2016
http://dx.doi.org/10.17843/rpmesp.2016.331.2017
ARTÍCULO ESPECIAL
Sugerencias a partir del análisis de sensibilidad de un modelo matemático de transmisión de chikungunya
Suggestions for chikungunya control based on a sensitivity analysis of a mathematical model
David Requena1, José L. Segovia-Juárez2
1 Laboratorio de Informática y Biología Molecular. Universidad Peruana Cayetano Heredia. Lima, Perú.
2 Instituto Nacional de Salud. Lima, Perú.
a Magister en Informática Biomédica; b Ph.D. en ciencias de la Computación
RESUMEN
La fiebre chikungunya afecta seriamente la salud de las personas, causando dolores articulares crónicos e incluso discapacidad. Es transmitida por picadura de los mosquitos Aedes aegypti y Aedes albopictus. Se han reportado brotes en diversas partes del mundo, incluyendo Latinoamérica. Estudios de modelamiento matemático de dichos brotes han calculado valores de parámetros epidemiológicos. En base a ellos, se elaboró un modelo matemático para simular un brote epidémico de chikungunya en una población local, transmitido desde una población vecina infectada. Mediante análisis de sensibilidad e incertidumbre se obtuvo que la tasa de transmisión mosquito-humano y humano-mosquito son las variables con mayor correlación con la cantidad de infectados, la cual se pierde significativamente a partir de los 60 días del primer caso en la población vecina. Se recomienda tomar esto en cuenta al planificar medidas de control sobre dichas variables como aislamiento de infectados, repartición de mosquiteros y repelentes, fumigación, entre otras.
Palabras clave: Infección por el virus Chikungunya; Control de enfermedades transmisibles; Técnicas de apoyo a la toma de decisiones (fuente: DeCS BIREME).
ABSTRACT
Chikungunya fever seriously affects peoples’ health and causes chronic joint pain and even disability. Chikungunya is transmitted by the bite of Aedes aegypti and Aedes albopictus. Outbreaks have been reported in throughout the world, including Latin America. Mathematical modeling studies of these outbreaks have calculated the values of various epidemiological parameters. Based on them, a mathematical model was prepared to simulate a chikungunya outbreak in a local population, which was transmitted from an neighboring infected population. A sensitivity and uncertainty analysis revealed that the mosquito-to-human and human-to-mosquito transmission rates are the variables with the highest correlation with the number infected people, which were greatest at 60 days after the first case in the neighboring population. Therefore, it is recommended to take this into consideration when planning policies to control such variables as isolation of infected people, distribution of mosquito netting and repellents, fumigation, among others.
Key words: Chikungunya virus infection; Communicable disease control; Decision support techniques (source: MeSH NLM).
INTRODUCCIÓN
La fiebre chikungunya es una enfermedad causada por la infección del virus chikungunya, el cual es transmitido al ser humano por picadura de los mosquitos hembra de las especies Aedes aegypti y Aedes albopictus (1).
Sus principales síntomas son fiebre y fuertes dolores articulares, además de causar dolores musculares, dolores de cabeza, náuseas, cansancio y erupciones cutáneas. El dolor causado en las articulaciones puede durar incluso meses o años, volviéndose crónico y llegando a causar discapacidad. Además de afectar seriamente la salud de las personas, esta enfermedad puede causar incluso la muerte (2).
Hasta hace unos años, el virus chikungunya se encontraba localizado principalmente en el continente africano. Sin embargo, actualmente ha sido reportado en 44 países de climas tropicales-cálidos y ha afectado a millones de personas en el mundo (3). A pesar de ello, es considerada una de las enfermedades olvidadas o desatendidas.
Recientemente se han reportado brotes de chikungunya en Europa, Asia e islas del océano Índico. Uno de los casos más estudiados han sido el caso de la isla Reunión el 2005-2006 (4,5). En dicho brote se infectaron aproximadamente 266 mil de los 785 mil habitantes, y se produjeron 200 muertes relacionadas a la infección. También se informó de brotes en Italia en el 2007 (6) y Camboya en el 2012 (7,8). Estos brotes han sido relacionados a una nueva variante de chikungunya (CHIK-R) (9) transmitida principalmente por el vector A. albopictus, el cual se reporta que es más efectivo para transmitir la infección que A. aegypti (10).
Esta enfermedad ha empezado a emerger y reemerger en las zonas endémicas debido a fenómenos como cambios climáticos (11–13). Además de la mutación genética adaptativa del virus (10), lo cual ha favorecido su diseminación en los mosquitos (14). El desplazamiento de las personas infectadas ha llevado la enfermedad a diversas partes del mundo. La transmisión ha sido favorecida especialmente en los entornos tropicales de los países en vías de desarrollo, como Perú, donde los recursos limitados debilitan los esfuerzos para la prevención (15).
El Perú se encuentra rodeado de países donde se ha reportado la enfermedad y ha habido brotes epidémicos(16), lo cual aumenta el riesgo de casos importados por migraciones fronterizas. El 9 de junio de 2015 se reportó el primer caso autóctono de chikungunya en Perú (17).El país cuenta con 18 regiones con infestación de A. aegypti y condiciones que facilitarían la introducción y diseminación del virus, lo cual representa un riesgo inminente para la salud pública (15).
En estas condiciones cobra mayor importancia la optimización del uso de los recursos disponibles. Ello se puede lograr mediante planeamiento estratégico asistido por modelos computacionales (9).
Existen estudios en la literatura científica donde mediante modelamiento matemático se ha abordado la transmisión del virus chikungunya. Esta ha sido abordada para distintos brotes y desde diferentes enfoques. Polettiet al. (6) modelaron el brote en Italia (2007), analizando la eficacia de las medidas de control empleadas. Yakob et al. (18) modelaron el brote de Réunion (2006) y Robinson et al. el brote en una zona rural en Camboya (8). En ambos, consideraron por separado los infectados sintomáticos de los asintomáticos, para un mejor ajuste a los datos reportados. Otros estudios han analizado factores adicionales, como considerar un periodo de incubación más corto en A. albopictus (19,20) y el efecto de posibles estrategias de control como reducción de larvas, prevención y tratamiento de la enfermedad (21), evaluando los parámetros que tienen más impacto en el tiempo de aparición y tamaño del pico de la curva epidémica de infectados (9), entre otros. Estos estudios proveen de importantes detalles sobre los parámetros, la dinámica y posibles estrategias control de la epidemia de chikungunya. Ello permite simular posibles escenarios de un brote epidémico, como el estudio de Ruiz-Moreno et al. para Estados Unidos (22), de Cauchemez et al. para el Caribe (23) y el de Massad et al. para áreas endémicas de dengue (24). Además, en otros estudios se ha mostrado cómo el análisis global de sensibilidad e incertidumbre, usando como índice la correlación parcial de coeficientes, permite conocer comparativamente cómo la variación de las variables afectan a los outputs de un modelo (25,26).
Ante la expansión actual de la epidemia de chikungunya es necesario entender la dinámica del avance de la epidemia entre poblaciones vecinas, y poder tomar medidas de control tempranas. Para ello, es necesario tener una idea de qué tanto efecto tendrían las medidas de control a tomar a medida que avanza la epidemia. En el presente estudio mostramos los resultados del análisis computacional de un modelo matemático desarrollado para simular una epidemia de chikungunya. Este modelo considera dos poblaciones vecinas, una recién infectada y otra completamente susceptible. Se utilizaron parámetros epidemiológicos calculados para brotes recientes de chikungunya en otros países, transmitidas por el vector A. albopictus y con datos poblacionales de la región de Tumbes (Perú). Se realizó un análisis global de sensibilidad e incertidumbre en este modelo para identificar los parámetros que tienen mayor correlación con la incidencia de infectados.
METODOLOGÍA
EL MODELAMIENTO MATEMÁTICO
En base a los grupos de personas considerados en otros modelos de chikungunya recientemente publicados (6,8,9,18–22), se desarrolló un modelo matemático de la transmisión considerando dos poblaciones de humanos y de mosquitos (Figura 1). Se consideró una población local (L) completamente susceptible y una población vecina (V) a la cual llegará un infectado.
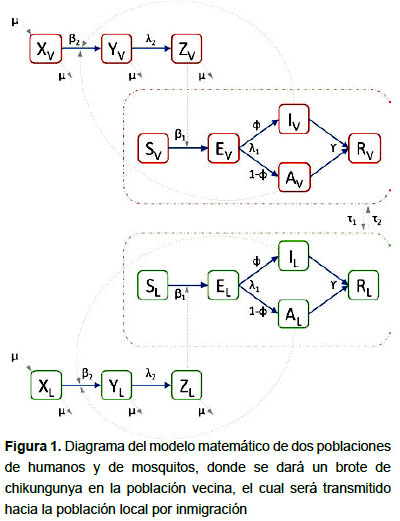
Para cada población humana, se considera un grupo de individuos susceptibles (Grupo S), los cuales pueden resultar infectados con el virus tras recibir la picadura de un mosquito infeccioso (Grupo Z). Los individuos infectados podrán desarrollar síntomas (Grupo I) o permanecer asintomáticos (Grupo A). Con el paso de los días, los infectados se irán recuperando (Grupo R).
Para cada población de mosquitos, se considera un grupo de mosquitos susceptibles (Grupo X), los cuales se infectarán con el virus chikungunya (Grupo Y) al picar humanos infectados. Tras unos días, estos individuos serán infecciosos (Grupo Z). Adicionalmente, se considera la ocurrencia de nacimientos y muerte natural en las poblaciones de mosquitos.
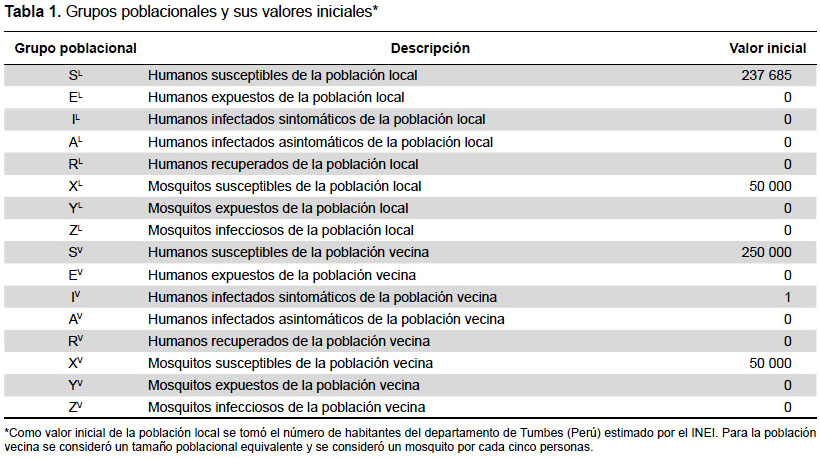
Los grupos poblacionales y los valores iniciales considerados para ellos, se muestran en la Tabla 1. Para el número inicial de habitantes de la población local, se consideró el número de personas del departamento de Tumbes (Perú) estimado por el Instituto Nacional de Estadística e Informática (27). Los parámetros epidémicos considerados se describen en la Tabla 2, la cual incluye los valores mínimo, central y máximo. Dichos valores se obtuvieron de lo reportado en otros modelos de chikungunya del 2007 en adelante (8,9,18,28), en los cuales fueron estimados en base a la data de sus correspondientes brotes epidémicos.
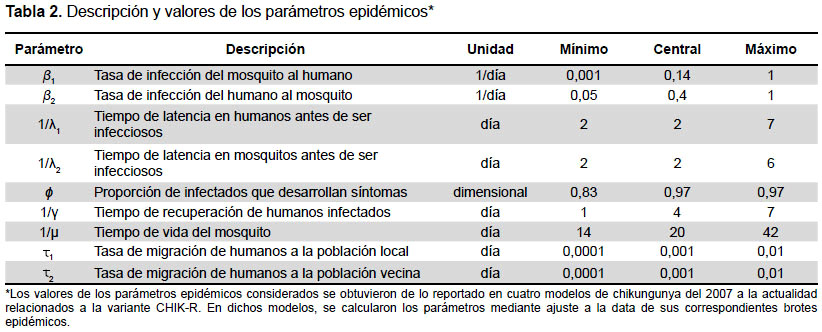
Las ecuaciones empleadas para modelar la dinámica de la transmisión descrita anteriormente se muestran a continuación:
Dinámica de la población local:
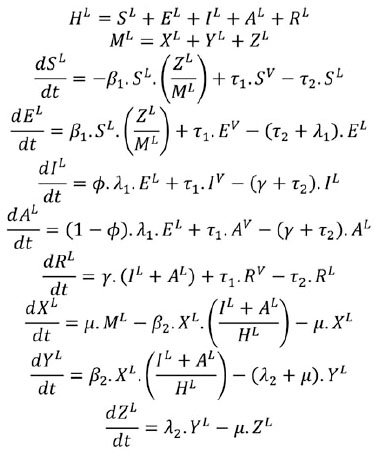
Dinámica de la población vecina:
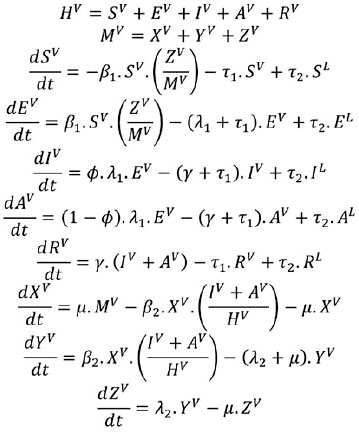
SUPUESTOS
Para el modelo matemático se consideró que la enfermedad es causada por una sola cepa de chikungunya, la cual se contagia solamente a través de picadura. Se tomó en cuenta una sola especie de mosquito Aedes. En los humanos infectados se considera que el tiempo de latencia para el desarrollo de síntomas coincide con el tiempo de latencia a partir del cual pueden contagiar a los mosquitos. Solamente los humanos sintomáticos o asintomáticos pueden contagiar a los mosquitos. Se asume que cada población está homogéneamente distribuida y todos los individuos tienen la misma probabilidad de interactuar con los mosquitos de su localidad. La probabilidad de transmisión de la enfermedad se considera constante para cualquier individuo a través del tiempo y en cualquier lugar. El modelo considera una sola oleada de chikungunya, con flujo solamente entre poblaciones humanas (y no de mosquitos) por inmigración y emigración. Las personas que se recuperan desarrollan inmunidad total.
ANÁLISIS DE SENSIBILIDAD E INCERTIDUMBRE
Se realizó un análisis global sensibilidad e incertidumbre usando el índice la correlación parcial de coeficientes, el cual permite analizar cualitativa y cuantitativamente los efectos de variación de los parámetros sobre el outcome de un modelo (25). Esto ha sido aplicado en el modelamiento matemático de epidemias, permitiendo determinar cómo influyen los parámetros del modelo en la dinámica de expansión de la epidemia (26). Los parámetros considerados para este análisis fueron la tasa de infección del mosquito al humano (β1), del humano al mosquito (β2) y las tasas de migración (τ1 y τ2).
Para realizar este análisis, se realizó la exploración del espacio paramétrico multidimensional mediante el muestreo aleatorio de valores en los intervalos de los paramétricos (Tabla 2) usando el método de Latin Hypercube Sampling (LHS) (29), asumiendo una distribución uniforme de los parámetros e independencia estadística entre ellos. Con estos conjuntos de valores se simularon diferentes escenarios. Se analizó el efecto de la variación de los parámetros mediante coeficientes de correlación parcial (PRCC) (26). Esto se realizó empleando el programa "crun" desarrollado por Segovia et al. (30), el cual permite realizar LHS y PRCC.
RESULTADOS
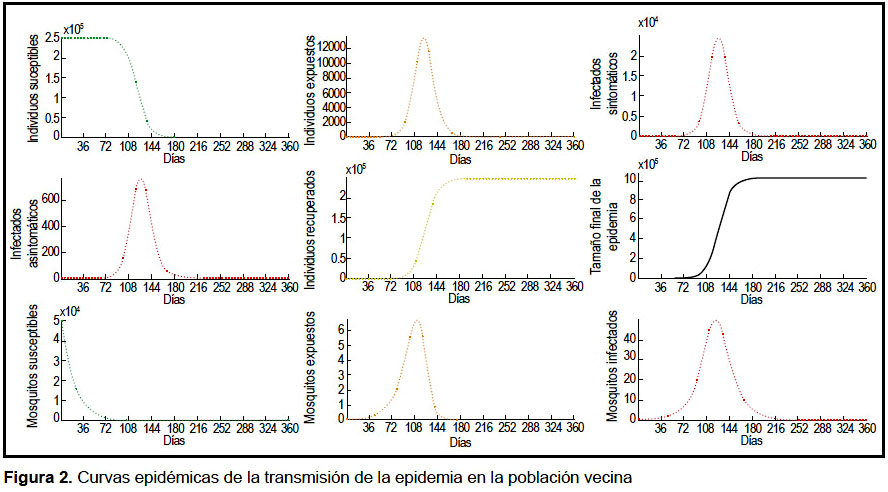
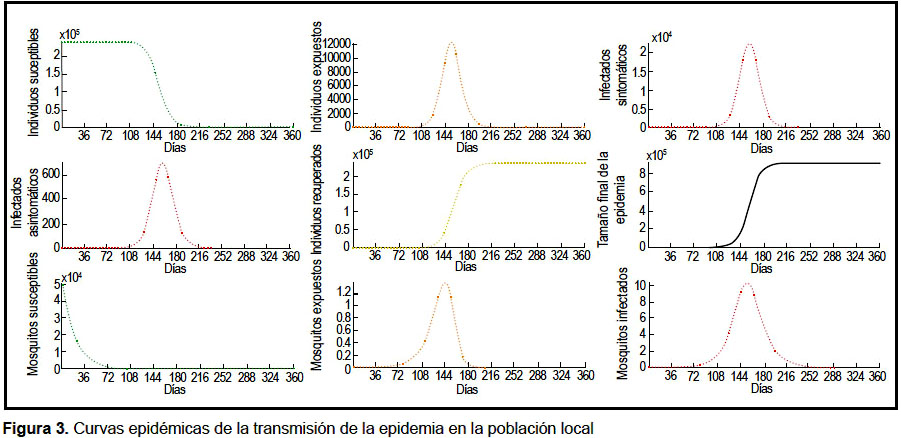
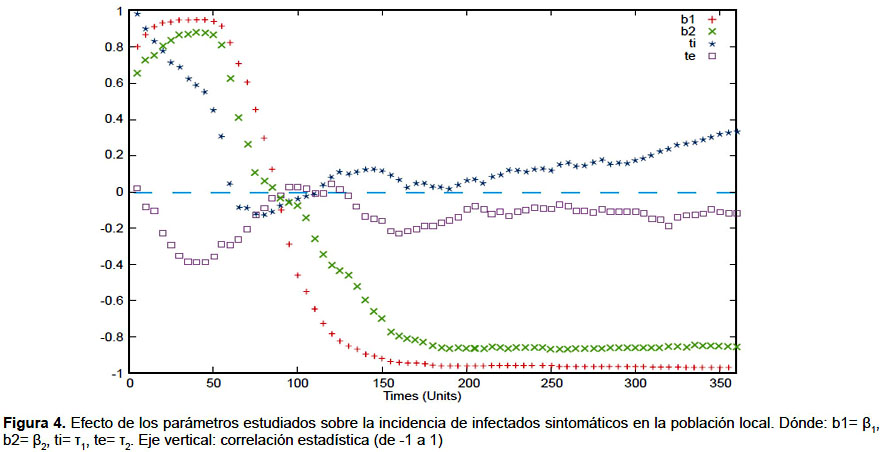
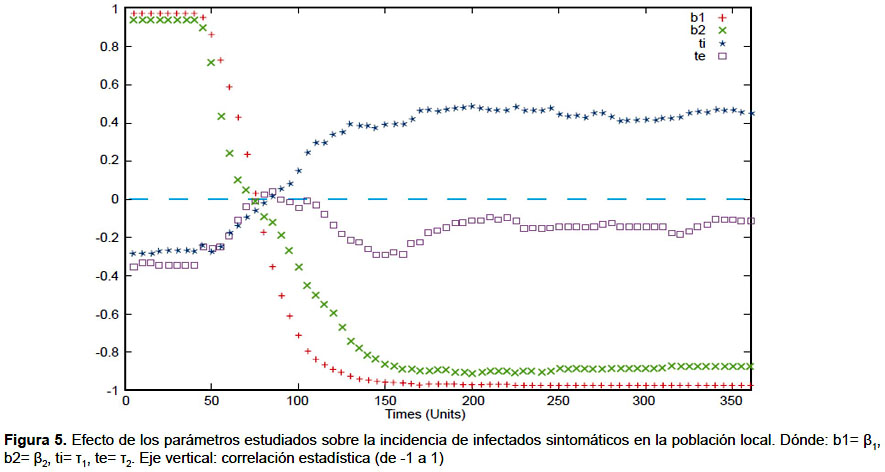
Los valores iniciales fueron asignados al día 1 del brote. El pico en el número de infectados sintomáticos y asintomáticos en la población vecina se logra el día 126 y en la población local el día 158. Las gráficas de la dinámica de la epidemia se muestran en las figuras 2 y 3. En el análisis de sensibilidad e incertidumbre se obtuvo que, a excepción de la tasa de emigración, los parámetros evaluados tienen correlación positiva con el aumento de infectados sintomáticos locales, siendo los de mayor efecto β1 y β2 (Figuras 4 y 5). Sin embargo, la correlación de las variaciones de estos dos parámetros con la variación de la incidencia de infectados pierde significancia a partir del día 60.
CONCLUSIONES
La fiebre chikungunya es una amenaza importante para los países con zonas tropicales y poblaciones de A. aegypti y A. albopictus. Diversos estudios muestran cómo la alta transmisibilidad de este virus puede conducir a una rápida diseminación y brotes severos (23). Por ello, es importante reaccionar tempranamente y tomar medidas de control.
En una realidad económica como la peruana, los limitados recursos disponibles para las medidas de control restringen los esfuerzos por controlar la enfermedad. Por ello, cobra mayor importancia estudios como este, donde se estudia el efecto de parámetros epidémicos vinculados a usuales medidas de control y el tiempo hasta el cual tienen impacto sobre la incidencia de infectados.
El modelo presentado tiene limitaciones, las cuales se originan tras los supuestos considerados. Sin embargo, una limitación adicional es la ausencia de datos locales. Esto debido a que la epidemia recién entraba al Perú al momento del estudio, los datos de los parámetros epidémicos se han obtenido de otros brotes, pertenecientes a entornos socioeconómicos y medioambientales distintos y teniendo como vector transmisor principal a A. albopictus. En Perú, en cambio, se estima que existe una mayor abundancia de A. aegypti. Sin embargo, se desconoce la proporción real ya que solamente se monitorea el índice aédico en general.
A pesar de ello, la dinámica epidémica obtenida en la población vecina es consistente con lo reportado en los otros estudios disponibles en la literatura, los cuales hacen buen ajuste con brotes recientes de chikungunya relacionados a la variante circulante (9). De las simulaciones, se obtiene que en la población local, el pico de infectados se alcanza en solo 157 días después de la primera infección en la población vecina. Esto es importante pues representa una alerta para las poblaciones susceptibles, tras la detección de un caso sintomático en una población vecina.
El uso de LHS/PRCC en el análisis de sensibilidad e incertidumbre ha demostrado ser útil en el análisis de modelos epidemiológicos, permitiendo cuantificar el efecto la variación de las variables de entrada sobre las variables de interés (25,26). Su aplicación en este estudio ha permitido determinar que las variables con mayor efecto sobre la variación del número total de infectados son la tasa de infección del mosquito al humano (β1) y del humano al mosquito (β2). El primero se suele controlar mediante el uso de repelentes y mosquiteros y, además, reduciendo el número de mosquitos infectados mediante la fumigación de criaderos. También se suele regular la tasa de transmisión del humano al mosquito, mediante medidas relacionadas al aislamiento de los infectados. Al respecto, una conclusión resaltante es que las medidas de control que busquen reducir estas tasas causarían impacto significativo en la reducción de la cantidad de infectados solamente hasta el día 60, el cual es antes de alcanzar el punto más alto de incidencia de infectados por la epidemia. Luego de ello, su correlación con la disminución de la incidencia de infectados va disminuyendo y deja de ser significativa. Es muy importante tener esto en cuenta al tomar acciones para el control de la epidemia vinculadas a estas tasas, enfocando el mayor esfuerzo tempranamente. De lo contrario, a medida que avance el brote epidémico irán perdiendo su impacto en contener la expansión de la epidemia.
Contribuciones de autoría: JLSJ identificó el problema, la necesidad del estudio y planteó el proyecto. DR realizó la revisión bibliográfica, el diseño del modelo matemático, el planteamiento de las ecuaciones y las simulaciones computacionales. JLSL y DR analizaron los resultados y obtuvieron las conclusiones del estudio.
Fuentes de financiamiento: este estudio fue financiado por el Centro Nacional de Salud Pública del Instituto Nacional de Salud de Perú.
Conflictos de interés: los autores declaran no tener conflictos de interés, que hayan influenciado en el desarrollo y las conclusiones del presente estudio.
REFERENCIAS BIBLIOGRÁFICAS
1. Pialoux G, Gaüzère B-A, Jauréguiberry S, Strobel M. Chikungunya, an epidemic arbovirosis. Lancet Infect Dis. 2007;7(5):319–27. doi: http://dx.doi.org/10.1016/S1473-3099(07)70107-X. [ Links ]
2. Robinson MC. An epidemic of virus disease in Southern Province, Tanganyika Territory, in 1952-53. I. Clinical features. Trans R Soc Trop Med Hyg. 1955;49(1):28–32. [ Links ]
3. Centers for Disease Control and Prevention. Chikungunya virus [Internet]. Atlanta: CDC; 2015 [cited 2015 Apr 10]. Available from: http://www.cdc.gov/chikungunya/geo/index.html. [ Links ]
4. Renault P, Solet JL, Sissoko D, Balleydier E, Larrieu S, Filleul L, et al. A major epidemic of chikungunya virus infection on Reunion Island, France, 2005-2006. Am J Trop Med Hyg. 2007;77(4):727–31. [ Links ]
5. Gérardin P, Guernier V, Perrau J, Fianu A, Le Roux K, Grivard P, et al. Estimating Chikungunya prevalence in La Réunion Island outbreak by serosurveys: Two methods for two critical times of the epidemic. BMC Infect Dis. 2008;8:99. doi: 10.1186/1471-2334-8-99. [ Links ]
6. Poletti P, Messeri G, Ajelli M, Vallorani R, Rizzo C, Merler S. Transmission potential of chikungunya virus and control measures: the case of Italy. PloS One. 2011;6(5):e18860. doi: 10.1371/journal.pone.0018860. [ Links ]
7. Centers for Disease Control and Prevention (CDC). Chikungunya outbreak-Cambodia, February-March 2012. MMWR Morb Mortal Wkly Rep. 2012;61:737–40. [ Links ]
8. Robinson M, Conan A, Duong V, Ly S, Ngan C, Buchy P, et al. A model for a chikungunya outbreak in a rural Cambodian setting: implications for disease control in uninfected areas. PLoS Negl Trop Dis. 2014;8(9):e3120. doi: 10.1371/journal.pntd.0003120. [ Links ]
9. Manore CA, Hickmann KS, Xu S, Wearing HJ, Hyman JM. Comparing dengue and chikungunya emergence and endemic transmission in A. aegypti and A. albopictus. J Theor Biol. 2014;356:174–91. doi: 10.1016/j.jtbi.2014.04.033. [ Links ]
10. Tsetsarkin KA, Vanlandingham DL, McGee CE, Higgs S. A single mutation in chikungunya virus affects vector specificity and epidemic potential. PLoS Pathog. 2007;3(12):e201. [ Links ]
11. Anyamba A, Linthicum KJ, Small JL, Collins KM, Tucker CJ, Pak EW, et al. Climate teleconnections and recent patterns of human and animal disease outbreaks. PLoS Negl Trop Dis. 2012;6(1):e1465. doi: 10.1371/journal.pntd.0001465. [ Links ]
12. Waldock J, Chandra NL, Lelieveld J, Proestos Y, Michael E, Christophides G, et al. The role of environmental variables on Aedes albopictus biology and chikungunya epidemiology. Pathog Glob Health. 2013;107(5):224–41. doi: 10.1179/2047773213Y.0000000100. [ Links ]
13. Perkins TA, Metcalf CJE, Grenfell BT, Tatem AJ. Estimating Drivers of Autochthonous Transmission of Chikungunya Virus in its Invasion of the Americas. PLoS Curr. 2015;7. doi: 10.1371/currents.outbreaks.a4c7b6ac10e0420b1788c9767946d1fc. [ Links ]
14. Vega-Rúa A, Zouache K, Girod R, Failloux AB, Lourenço-de-Oliveira R. High level of vector competence of Aedes aegypti and Aedes albopictus from ten American countries as a crucial factor in the spread of Chikungunya virus. J Virol. 2014;88(11):6294–306. doi: 10.1128/JVI.00370-14. [ Links ]
15. Ministerio de Salud del Perú. Dengue y Chikungunya [Internet]. Lima: MINSA; 2015 [cited 2015 Mar 3]. Available from: http://www.minsa.gob.pe/portada/Especiales/2014/chikungunya/index.asp. [ Links ]
16. Centers for Disease Control and Prevention. Countries and territories where chikungunya cases have been reported (as of February 24, 2015) [Internet]. Atlanta: CDC; 2015 Feb [cited 2015 Mar 3]. Available from: http://stacks.cdc.gov/view/cdc/27932. [ Links ]
17. Ministerio de Salud del Perú. Sala de prensa. Ministro de Salud confirmó primer caso autóctono de fiebre chikungunya en el país [Internet]. Lima: MINSA; Junio de 2014 [cited 2015 Jun 10]. Available from: http://www.minsa.gob.pe/?op=51¬a=16615.
18. Yakob L, Clements AC. A mathematical model of chikungunya dynamics and control: the major epidemic on Réunion Island. PloS One. 2013;8(3):e57448. doi: 10.1371/journal.pone.0057448. [ Links ]
19. Dumont Y, Chiroleu F, Domerg C. On a temporal model for the Chikungunya disease: modeling, theory and numerics. Math Biosci. 2008;213(1):80–91. doi: 10.1016/j.mbs.2008.02.008. [ Links ]
20. Dumont Y, Chiroleu F. Vector control for the Chikungunya disease. Math Biosci Eng. 2010;7(2):313–45. doi: 10.3934/mbe.2010.7.313. [ Links ]
21. Moulay D, Aziz-Alaoui MA, Kwon HD. Optimal control of chikungunya disease: larvae reduction, treatment and prevention. Math Biosci Eng. 2012;9(2):369–92. doi: 10.3934/mbe.2012.9.369. [ Links ]
22. Ruiz-Moreno D, Vargas IS, Olson KE, Harrington LC. Modeling dynamic introduction of Chikungunya virus in the United States. PLoS Negl Trop Dis. 2012;6(11):e1918. doi: 10.1371/journal.pntd.0001918. [ Links ]
23. Cauchemez S, Ledrans M, Poletto C, Quenel P, de Valk H, Colizza V, et al. Local and regional spread of chikungunya fever in the Americas. Euro Surveill. 2014;19(28):20854. [ Links ]
24. Massad E, Ma S, Burattini MN, Tun Y, Coutinho FA, Ang LW. The risk of chikungunya fever in a dengue-endemic area. J Travel Med. 2008;15(3):147–55. doi: 10.1111/j.1708-8305.2008.00186.x. [ Links ]
25. Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol. 2008;254(1):178–96. 10.1016/j.jtbi.2008.04.011.
26. Blower SM, Dowlatabadi H. Sensitivity and Uncertainty Analysis of Complex Models of Disease Transmission: An HIV Model, as an Example. Int Stat Rev. 1994;62(2):229-43. [ Links ]
27. Población Estimada al 30 de junio, por años calendario y sexo, según departamento [Internet]. Lima: Instituto Nacional de Estadística e Informática (INEI); 2015 [cited 2015 Mar 3]. Available from: https://www.inei.gob.pe/media/MenuRecursivo/Cap03025B.xls. [ Links ]
28. Manore CA, Hickmann KS, Hyman JM, Foppa IM, Davis JK, Wesson DM, et al. A network-patch methodology for adapting agent-based models for directly transmitted disease to mosquito-borne disease. J Biol Dyn. 2015;9:52-72. doi: 10.1080/17513758.2015.1005698. [ Links ]
29. Helton JC, Davis FJ. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab Eng Syst Saf. 2003;81(1):23–69. [ Links ]
30. Segovia-Juarez JL, Ganguli S, Kirschner D. Identifying control mechanisms of granuloma formation during M. tuberculosis infection using an agent-based model. J Theor Biol. 2004;231(3):357–76. [ Links ]
Correspondencia:
David Rubén Requena Anicama
Dirección: Laboratorio de Bioinformática y Biología Molecular.
Laboratorios de Investigación y Desarrollo, Universidad Peruana Cayetano Heredia.
Av. Honorio Delgado 430, San Martin de Porres. Código Postal: 15102. Lima, Perú.
Teléfono: (511) 979790920
Correo electrónico: david.requena.a@upch.pe
Recibido: 01-09-15
Aprobado: 09-03-16














