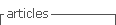La individualización de los procesos educativos a partir de la atención de las distintas potencialidades de los alumnos existentes en las aulas, constituye una premisa fundamental de una educación inclusiva y de calidad. Esta cuestión es relevante en un mundo competitivo y globalizado con constantes innovaciones y cambios de necesidades (Macià & Garreta, 2018), que demandan nuevas formulaciones de los diseños didácticos. En este sentido, cobra un especial protagonismo el trabajo de las disciplinas STEM (Ciencias, Tecnología, Ingeniería y Matemáticas por sus siglas en inglés) por su aporte destacado a una sociedad basada en el conocimiento (García-Perales & Almeida, 2019; UNESCO, 2019). En esta investigación, nos centramos en el desempeño de los alumnos en las Matemáticas. Más concretamente, pretendemos analizar, desde el punto de vista cuantitativo y cualitativo, la resolución de pruebas de Matemáticas por alumnos identificados con características de superdotación o altas capacidades tomando como referencia la comparativa con otros escolares con buen rendimiento en esta área.
Habilidad matemática
La generalización a la vida cotidiana de las competencias matemáticas y su interdisciplinariedad justifican su integración en los procesos de enseñanza y aprendizaje como competencia clave, en este caso denominada Competencia matemática y competencias básicas en ciencia y tecnología. Además, esta disciplina curricular se conforma como básica para el desenvolvimiento en la vida diaria y el desarrollo intelectual de los alumnos (Gilat & Amit, 2013). La resolución de tareas matemáticas posibilita, en particular desde el desarrollo de trabajo grupal, la estimulación del pensamiento crítico y las habilidades de resolución de problemas (Koçak, Bozan, & Isik, 2009) en los diferentes contextos de la vida de los alumnos (Jordan, Glutting, & Ramineni, 2010).
En efecto, la actividad de resolución de problemas presente en las Matemáticas incentiva a una actitud pensante y reflexiva del alumnado versus una actitud pasiva de escuchar y repetir procesos en la clase (Viseu, Fernandes, & Gomes, 2016). Se asume que el aprendizaje de las Matemáticas se convierte en estrategias cognoscitivas de problematizar situaciones o formalizar problemas, delinear y concretar estrategias de resolución, monitorizar el proceso de resolución y explicar hechos y procedimientos (Klieme, 2004; National Council of Teachers of Mathematics, 2007). Se trata de estrategias de resolución de problemas que Polya (1986) organiza de la siguiente forma: (i) tentativa y error o intención de “adivinar” el resultado a través de un algoritmo con base en los datos proporcionados por el problema; (ii) uso de patrones o soluciones particulares de un problema que se generalizan a otros para encontrar su solución; (iii) resolución de un problema por medio de una versión más simple o resolución través de una alteración transitoria de un problema complejo en una versión más simplificada; (iv) trabajo desde el final hasta el principio, se comienza a resolver el problema a partir del estado final y a través de esto se toma la resolución respectiva hasta alcanzar el estado inicial; (v) simulación a través de la dramatización o la realización de una experiencia se efectúa la resolución del problema. Al mismo tiempo hay que tener en cuenta la tipología de respuestas, recurriendo a la propuesta de Cañellas y Rassetto (2013): (i) idiosincrática: producción sin ningún significado y con ello no interpretable; (ii) pictográfica: consiste en la utilización de dibujos o figuras para la representación de cantidades; (iii) icónica: utilización de símbolos diseñados por el propio escolar para representar objetos; (iv) numérica: implica la utilización de números y operaciones aritméticas; (v) simbólica-convencional: cuando se usan símbolos numéricos convencionales para la representación de objetos en su totalidad. Otras investigaciones recalcan la importancia de estas taxonomías para el análisis cualitativo del desempeño del alumnado en la resolución de problemas matemáticos, incluyendo el papel del conocimiento y control metacognitivo de los mismos (Arroyo, Korzeniowski, & Espósito, 2014; Cázares, Páez, & Pérez, 2020; García, Cueli, Rodríguez, Kravec, & González-Castro, 2015).
El aprendizaje y desempeño en las Matemáticas se puede entender como un proceso en el que inciden múltiples factores (Almeida, Guisande, Primi, & Lemos, 2008; Desco et al., 2011; Farfán & Simón, 2017; Rodríguez & Guzmán, 2018). La investigación destaca que el rendimiento académico podría, en parte, estar explicado por las capacidades intelectuales o cognitivas de los alumnos (Almeida, Araújo, Sainz-Gómez, & Prieto, 2016; García-Perales & Almeida, 2019; Morosanova, Fomina, & Bondarenko, 2015) y por sus actitudes y motivaciones hacia su aprendizaje (Cueli, García, & González-Castro, 2013; De La Rosa, 2007; Mato, Espiñeira, & Chao, 2014; Tourón, Lizasoaín, Castro, & Navarro, 2012). Cuando los escolares tienen más interés y creencia en su aprendizaje como fuente de conocimiento, mejor será su rendimiento en esta materia (Figueiredo & Guimarães, 2019). A pesar de ello, también pueden tener incidencia otros factores de diversa índole, caso de los relativos al profesorado (Carey, Hill, Devine, & Szücs, 2016; Dowker, Sarkar, & Yen Looi, 2016; Schillinger, Vogel, Diedrich, & Grabner, 2018) y/o al ámbito familiar (Ferreira, Flores, & Casas-Novas, 2017; Rodríguez-Mantilla, Fernández-Díaz, & Jover, 2018).
Habilidad matemática y resolución de problemas
Las ediciones PISA (Programme for International Student Assessment) definen la competencia matemática como la capacidad de solucionar problemas en situaciones de mayor complejidad y que requieren conocimientos determinados y uso de estrategias específicas (Ministério de Educação e Ciência, 2018). A su vez, se apunta que los escolares con nivel de rendimiento 6 o superior en la prueba PISA para las Matemáticas (Ministerio de Educación y Formación Profesional, 2019, p. 64), nivel de rendimiento más elevado para los resultados de PISA, “saben formar conceptos, generalizar y utilizar información basada en sus investigaciones y modelizar situaciones de problemas complejos, y pueden utilizar su conocimiento en contextos relativamente atípicos”. Al mismo tiempo, se añade que estos alumnos excelentes en matemática (Ministerio de Educación y Formación Profesional, 2019, p. 64):
Pueden relacionar simultáneamente diferentes fuentes de información y representaciones e intercambiarlas entre ellas de manera flexible (…) pueden aplicar esta comprensión, así como su dominio de las operaciones y relaciones matemáticas simbólicas y formales para desarrollar nuevos enfoques y estrategias para abordar situaciones nuevas.
De esta manera, queda patente que dentro del aprendizaje de las Matemáticas, un aspecto fundamental es esta capacidad de resolución de problemas, incluyendo la habilidad para interpretar la información presentada y ejecutar razonamientos básicos apoyándose en representaciones de cualquier tipo (Duval, 1999; García, Betts, González-Castro, González-Pienda, & Rodríguez, 2016; Goldin & Janvier, 1998; Guven & Cabakcor, 2013; Ministerio de Educación y Formación Profesional, 2019; Organización para la Cooperación y el Desarrollo Económico, 2019).
Continuando con la delimitación conceptual de problema, Echenique (2006, p. 20) lo define como “una situación que un individuo o grupo quiere o necesita resolver y para la cual no dispone, en principio, de un camino rápido y directo que le lleve a la solución”. Cuando un escolar se enfrenta a un problema existe una falta de claridad entre el momento inicial y la finalidad a alcanzar, existiendo en ocasiones conceptualizaciones en los escolares que pueden derivar en errores (Jiménez & Verschaffel, 2014). Para ello, resulta necesario seleccionar aquello con más relevancia y delimitar una serie de pasos a seguir para su resolución, interviniendo un conjunto amplio de capacidades cognitivas como reflexión, análisis, actitud crítica, autonomía e iniciativa personal, toma de decisiones, lectura comprensiva, flexibilidad de pensamiento y perseverancia, entre otras. De esta forma, nos podemos encontrar un razonamiento de tipo analítico que busca el logro de un resultado por medio de procesos de similitudes o analogías entre los distintos elementos que componen el problema, un pensamiento de lo general a lo concreto y, por otro lado, otro tipo de razonamiento sintético en el que la búsqueda del resultado al problema se desarrolla de forma más directa y breve, un pensamiento de lo concreto a lo general.
Todas estas funciones cognitivas están presentes en la secuencia de etapas que Polya (1949, 1986) establece para la resolución de problemas: leer y comprender el problema, establecer un plan, ejecutarlo y examinar la solución obtenida. La concretización de estas etapas requiere la adopción de estrategias adecuadas que permitan obtener la solución a un problema dado. Musser e Shaughnessy (1980), agregan a las tres estrategias propuestas por Polya (1986), el trabajar en sentido inverso, o sea, partir del objetivo o de aquello que se quiere probar, en vez de partir de los datos, y simular la solución del problema a través de la realización de una experiencia, recopilando datos y tomando una decisión basada en el análisis de esos datos.
Habilidad matemática y superdotación
Se pretende analizar la manera en que los alumnos con altas capacidades o superdotación se enfrentan y solucionan problemas matemáticos. En este sentido, es importante aclarar lo que podemos entender por alumnos superdotados y, en segundo lugar, también lo que se entiende por alumnos matemáticamente talentosos. De forma muy breve, se entiende por alumnos superdotados aquellos que se destacan por sus habilidades intelectuales superiores cuando los comparamos con su grupo de edad o escolar de referencia. Internacionalmente se asume, siguiendo los resultados de distintas investigaciones, que este grupo de alumnos supone entre el 3% y el 5% de la población con capacidad superior en uno o más dominios, por ejemplo, académico, intelectual, social, motor, mecánico o artístico (McClain & Pfeiffer, 2012; Pfeiffer, 2009; Rocha et al., 2017). En términos clásicos, estos alumnos presentan un Cociente Intelectual (CI) igual o superior a 130, o sea, dos desviaciones típicas por encima de la media de la población (Official Norwegian Report -NOU, 2016; Pereira, Seabra-Santos, & Simões, 2003; Sak, 2020). Sin embargo, la superdotación es un fenómeno complejo asociado a las elevadas capacidades, no se circunscribe únicamente al factor inteligencia (Rocha, Perales & Almeida, 2020). Así, en la descripción de estos alumnos, los autores apuntan a la creatividad y la elevada implicación o motivación en las tareas de aprendizaje y de realización cognitiva, que combinadas con la elevada capacidad, se manifiesta en la facilidad y rapidez en el procesamiento de la información, fácil adquisición de contenidos y conceptos, vocabulario bastante amplio, motivación intrínseca en el aprendizaje, espíritu crítico, persistencia en las tareas y apertura a la experiencia (Gagné, 2018; Renzulli, 2018; Sternberg 2005; Tejera, Borges del Rosal, & Naveiras, 2017).
Son varias las propuestas de definiciones de superdotación, existiendo una evolución en la definición de tal concepto, aumentando el rango de habilidades intelectuales consideradas (por ejemplo, espíritu crítico, razonamiento matemático precoz e intereses más avanzados) y emocionales (por ejemplo, pensamiento moral elevado y empatía) en su caracterización (Al-Hroub & El Khoury, 2018). Así, la definición de superdotación abarca no solo los valores de CI o Cociente Intelectual en su propia identificación, también otras características individuales, como el desenvolvimiento en la tarea y la creatividad. De esta forma, las definiciones contemporáneas analizan y definen la superdotación de diversas formas, lo que lo hace tan relativo y dificulta la existencia de una definición universalmente aceptada (Sak, 2020).
Tal y como se verifica en el campo de la superdotación, la definición de talento matemático no es unánime, habiendo un intento constante a lo largo de los años para mejorar la comprensión de este constructo (Sheffield, 2016). Una de las definiciones más referenciadas es la de Krutetskii (1976), que define talento matemático como una capacidad única que contempla diversas competencias matemáticas que promueven éxito en el desempeño de tareas matemáticas en la escuela y en otros contextos. Así, siguiendo a Krutetskii (1976), estos alumnos con “espíritu matemático”, como Krutetskii (1976) acuña, manifiestan la capacidad de generalización rápida y amplia de relaciones y operaciones matemáticas y flexibilidad de procesos mentales, y una elevada predisposición para analizar el mundo a partir de una visión matemática. Parish (2014, 2019) refuerza esta noción, afirmando que los alumnos talentosos en el campo de las matemáticas tienden a destacar por sus habilidades para analizar, comprender y adquirir conocimientos matemáticos. En este sentido, identifica a niños con talento matemático como aquellos que poseen habilidades naturales excepcionales en la lectura de conceptos matemáticos, desde la comprensión hasta los procesos de aprendizaje. Los alumnos matemáticamente talentosos presentan, desde edades tempranas, una elevada actividad y motivación hacia las tareas en este campo junto a rapidez de comprensión de conceptos y algoritmos, alta capacidad de abstracción y gran flexibilidad de pensamiento (Krutetskii, 1976; Reyes-Santander & Karg, 2009; Tourón & Tourón, 2006). Además de esto, estos alumnos muestran tener una capacidad de raciocinio analítico, deductivo e inductivo, y por eso abordan los problemas matemáticos con elevada flexibilidad de pensamiento, en vez de seguir secuencias rígidas o un determinado patrón de raciocinio (Rotigel & Fello, 2004). Los alumnos talentosos en las Matemáticas consiguen responder mejor en estos dominios de orientación, organización y en la propia reflexión de las tareas propuestas, siendo más meticulosos en dar solución a un problema, dedicando más tiempo a pensar y planear la solución correspondiente e identificar las respectivas suposiciones para su posterior resolución (Budak, 2012; Sriraman, 2003). Estos alumnos requieren de metodologías de enseñanza que promuevan aprendizajes con mayor profundidad en la materia, resolución de problemas más complejos y abiertos, en lugar de tareas que involucran aprendizajes por repetición y práctica (Rotigel & Fello, 2004).
Todo este marco teórico enmarca la presente investigación, cuya finalidad es comprender, analizar y comparar a dos grupos de escolares, alumnos con superdotación detectada y alumnos con desarrollo típico y buen rendimiento en Matemáticas, para conocer cómo se diferencian en el manejo de estrategias complejas de resolución de problemas, incluyendo representaciones y tipo raciocinio utilizados para la ejecución de los problemas presentados.
Método
Participantes
Para la realización del presente estudio han sido seleccionados alumnos portugueses del 2º y 3º ciclo de enseñanza básica, con edades comprendidas entre los 10 y los 15 años (M = 12.13; DT = 1.51). Estos participantes han sido divididos en dos grupos de acuerdo con la identificación o no de superdotación. El primer grupo (n = 42) representa el grupo de alumnos con diagnóstico de altas capacidades (Grupo 1), está mayoritariamente formado por alumnos del sexo masculino (81%). El segundo grupo (n = 52) está constituido por alumnos con desarrollo típico y buen rendimiento en Matemáticas (Grupo 2), formado mayormente por alumnos del sexo femenino (59.6%). Señalar que no hay diferencias en el rendimiento académico de los alumnos en los dos grupos (identificados y no identificados), siendo en ambos grupos elevado tomando como referencia las calificaciones en el área de Matemáticas a fecha de junio del pasado curso escolar.
Medidas e instrumentos de medida
En el proceso de evaluación del desempeño matemático, principal variable de la investigación, se han utilizado dos pruebas de evaluación, una para cada etapa escolar en las que los participantes están escolarizados. Con la finalidad de asegurar la validez de contenido de ambos instrumentos, se ha contado con la colaboración de cinco expertos en el campo de las Matemáticas de diversas etapas educativas de enseñanza con más de quince años de experiencia docente impartiendo enseñanza de esta área en centros escolares, profesionales diferentes a los autores de la presente investigación.
Como instrumentos, tenemos la Prueba de Resolución de Problemas Matemáticos 1 (PRPM1) compuesta por 4 ítems y dirigida a alumnos de 2º ciclo de enseñanza básica; y la Prueba de Resolución de Problemas Matemáticos 2 (PRPM2) formada por 4 ítems y dirigida a alumnos de 3º ciclo de enseñanza básica (en el anexo final aparecen las dos pruebas utilizadas en este estudio, versión original en portugués o anexo 1 y versión traducida al castellano o anexo 2).
Cada ítem de los instrumentos ha sido evaluado con las siguientes categorías: Respuesta en blanco o incorrecto (0), parcialmente correcto (1), y totalmente correcto (2). Parcialmente correcto hace referencia a que el alumno no señala la solución correcta pero sí que se observa un abordaje y/o ejecución del problema próximo a lo requerido para lograr su solución. Al mismo tiempo, el tipo de tarea es diferente en los ítems de cada prueba: un ítem de producción, un ítem de comprensión, y dos ítems que combinan ambas. En el análisis cualitativo tomando en consideración las respuestas de los alumnos, se apreció su tipo de raciocinio (analítico, sintético o ninguno) y el tipo de representación tras tomar como punto de partida la propuesta de Cañellas y Rassetto (2013) señalada anteriormente (lenguaje natural, simbólica-numérica, pictórica, más de una representación y ningún tipo de representación utilizada). En la línea de las estrategias de resolución de problemas (Polya, 1986) han sido seleccionado las siguientes: resolución del problema a partir de una versión más simple, diseño de una figura o diagrama, diseño de una tabla, patrones y conjeturas, utilización de varias estrategias y ninguna.
Procedimiento
Para la recogida de las características sociodemográficas de la muestra del alumnado del Grupo 1, se ha solicitado la colaboración de una asociación que promueve actividades de enriquecimiento semanales con alumnos superdotados. Esta asociación, en la identificación de la superdotación, utiliza pruebas psicopedagógicas según el Modelo de los Tres Anillos de Renzulli (1986) o convergencia de tres factores: capacidad intelectual superior, elevada creatividad y motivación (Renzulli & Gaesser, 2015). Además de los instrumentos psicopedagógicos, bajo la consideración de una evaluación multidimensional, también se utilizan entrevistas semiestructuradas con los padres y la retroalimentación de los profesores mediante la cumplimentación de cuestionarios, donde debe evaluar la presencia de estas características de superdotación en el alumno en proceso de evaluación. Los alumnos del Grupo 2 provienen de una escuela privada y no están identificados con superdotación por la escuela y sus profesores. Se procuró agrupar a los alumnos de los dos grupos por etapa escolar. Se obtuvo consentimiento informado por escrito de los responsables institucionales, y el consentimiento de los niños y adolescentes para su participación en el estudio. La confidencialidad de la recogida de información ha sido garantizada y los datos se han codificado protegiendo la privacidad de los participantes. Después de haber recopilado la información sociodemográfica, los alumnos en grupos han tenido 45 minutos para la realización de su prueba matemática.
Los resultados cuantitativos han sido analizados estadísticamente con el software IBM/SPSS (versión 26.0). El análisis cualitativo ha sido realizado por parte de expertos e investigadores del presente estudio, todos ellos conocedores de los procesos de enseñanza y aprendizaje para las Matemáticas, considerando los formularios de las pruebas donde también los alumnos hacían sus cálculos y borradores en el proceso de resolución de las tareas.
Resultados
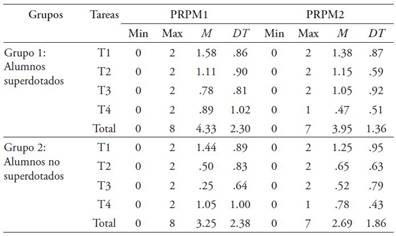
Los resultados aparecen expresados en dos apartados en función de la prueba de capacidad matemática administrada, PRPM1 y PRPM2 (en los anexos son presentadas las dos pruebas en sus versiones portuguesa y española, anexos 1 y 2). En la Tabla 1 se presentan los estadísticos descriptivos para cada una de las cuatro tareas; en ambas pruebas de matemática se consideraron los dos grupos de alumnos (identificados y no identificados con superdotación/altas capacidades).
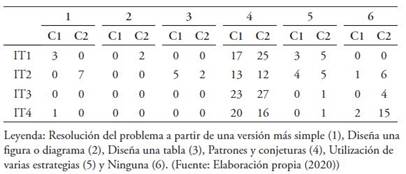
Tabla 1 Estadísticos descriptivos por tarea de ambas pruebas de resolución de problemas en los dos grupos de alumnos
Fuente: Elaboración propia (2020)
Como puede observarse, han aparecido tareas con distintos índices de dificultad tras analizar las puntuaciones medias de los alumnos para cada ítem. En la prueba PRPM1 la tarea 3 se presenta como la más difícil para los alumnos al obtener puntuaciones medias de .78 y .25 para ambos grupos, y la tarea 1 como la más fácil, puntuaciones medias de 1.58 y 1.44. En la prueba PRPM2 la tarea 4 aparece como la más difícil para los alumnos superdotados, media .47, y la tarea 3 para los no superdotados, media de .52, y la tarea 1 como la fácil para ambos grupos, medias de 1.38 y 1.25 respectivamente. Comparando los dos grupos de alumnos, observamos, tanto en la prueba PRPM1 como en la PRPM2, que los alumnos del Grupo 1 presentan medias más elevadas en las tareas 2 y 3, mientras que el Grupo 2 obtiene mejores resultados en la tarea 4. En la tarea 1 de las dos pruebas los dos grupos de alumnos se aproximan bastante en sus medias. Considerando la suma de puntuaciones de las cuatro tareas en las dos pruebas, se verifica que el Grupo 1 obtiene puntuaciones superiores a los del Grupo 2.
Analizando las discrepancias en las medias de los dos grupos de alumnos (t-test para muestras independientes), se señalan diferencias estadísticamente significativas en prueba PRPM1 a favor del Grupo 1 en la tarea 2 (t(1,37) = 2.182, p < .05) y en la tarea 3 (t(1,37) = 2.244, p < .05). En las tareas restantes y para el sumatorio global no se verifican diferencias estadísticamente significativas entre los dos grupos de alumnos. A su vez, en la prueba PRPM2, se verifican diferencias estadísticamente significativas a favor del Grupo 1 en la tarea 1 (t(1,53) = 2.730, p < .09), en la tarea 3 (t(1,53) = 2.193, p < .05) y en la puntuación global (t(1,53) = 2.682, p < .01). Por último, en la tarea 4 se observa una diferencia cuasi estadísticamente significativa a favor del Grupo 2 (t(1,53) = -1.952, p = .06).
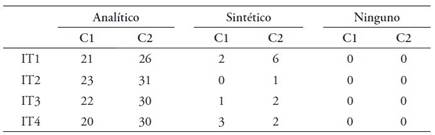
Tras analizar cualitativamente la resolución de los alumnos, se separa el análisis para cada una de las pruebas utilizadas (PRPM1 y PRPM2). En relación a la prueba PRPM1 se verifica que el raciocinio analítico ha sido el más utilizado por los dos grupos de alumnos en los cuatro ítems del instrumento, lo que significa que la mayor parte de los alumnos ha evidenciado esta forma de raciocinio (Tabla 2).
En las respuestas a la tarea 3 “Realiza las operaciones básicas que consideres necesarias y utiliza los siguientes números (3, 50, 7, 8, 30 y 1) una sola vez, de manera que el resultado sea 348”, se encontró una mayor proporción de alumnos del Grupo 1 que utilizó un raciocinio analítico, lo que podría explicar el mejor desempeño de este grupo. Asimismo, los alumnos del Grupo 1 presentan una resolución más desarrollada que los alumnos del Grupo 2, que tienden a realizar una propuesta de resolución más breve. En Figura 1 se ilustra como un alumno del Grupo 1 utiliza un esquema más organizado y de orden superior de complejidad que el señalado por el alumno del Grupo 2.
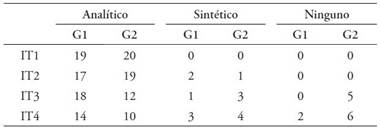
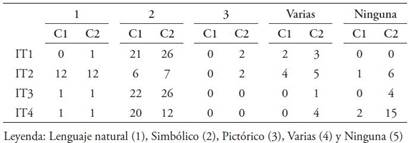
En relación al tipo de representación utilizada por el alumnado de cada grupo, se ha verificado que la representación de tipo simbólica-numérica ha sido la más común para ambos grupos y para las cuatro tareas de la prueba (Tabla 3).
Indicar que aparece un reparto diferente entre los dos grupos en la tarea 3. Aquí, 19 alumnos del Grupo 1 han elegido el tipo de representación simbólica-numérica frente a 14 alumnos del Grupo 2 (en este grupo 5 alumnos no han utilizado ningún tipo de representación para este ítem), como se presenta en la Figura 2.
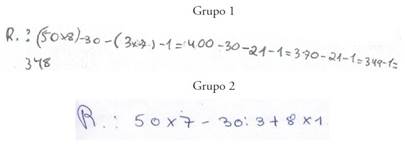
Fuente: Elaboración propia (2020)
Figura 2 Ejemplos de representación simbólica-numérica para alumnos de los Grupos 1 y 2
Por último, de acuerdo al tipo de estrategias de resolución de problemas utilizadas, no han aparecido diferencias relevantes en función de los dos grupos de alumnos (Tabla 4).
Asimismo, podemos resaltar que en la tarea 1 se encontraron 8 escolares del Grupo 1 que han utilizado varias estrategias de las señaladas anteriormente frente a solo 4 alumnos del Grupo 2, en ambos casos utilización de las estrategias de forma arbitraria; en tarea 4, 3 alumnos del Grupo 1 han buscado una versión más simple del problema tras simplificar el contenido del mismo para su resolución, frente a ninguno del Grupo 2; 7 alumnos del Grupo 1 han manejado la estrategia de patrones y conjeturas y solo 4 del Grupo 2; y en contraposición, 6 alumnos del Grupo 2 y solo 1 del Grupo 1 no han utilizado ningún tipo de estrategia, mayormente el ejercicio ha aparecido en blanco o bien incorrecto y la estrategia utilizada no puede incluirse en ninguno de los tipos de estrategias considerados.
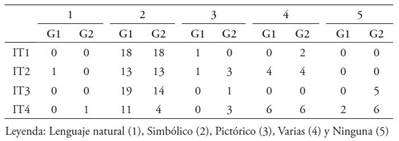
Analizando ahora los resultados para la PRPM2, se ha observado diferencia en la tarea 4 (tarea de comprensión), habiendo más alumnos del Grupo 1 con puntuación de 0 o tarea incorrecta, en cuanto en la tarea 2 ha habido más respuestas incorrectas en el Grupo 2 (Tabla 5).
De acuerdo al raciocinio utilizado, ha aparecido para cada grupo de alumnos lo siguiente:
Analizando cualitativamente la producción de los alumnos, se ha contemplado el equilibrio en tipos de raciocinio, analítico y sintético, entre el alumnado de ambos grupos, y en todas las tareas se ha verificado que todos los alumnos intentan desarrollar su raciocinio en detrimento de presentar respuestas intuitivas sin ninguna fundamentación. A su vez, al igual que ha ocurrido con la PRPM1, en la PRPM2 la representación simbólica-numérica ha sido la más utilizada por los dos grupos de alumnos y para las cuatro tareas de la prueba (Tabla 7).
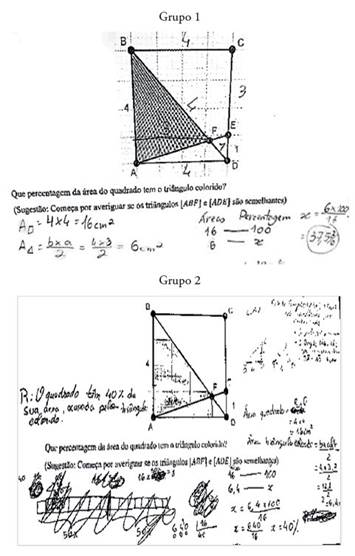
En el ítem 4 han aparecido diferencias debidas a la mayor proporción de alumnos del Grupo 1 que ha hecho uso de la representación simbólica-numérica, 20 frente a 12 en el Grupo 2. Además, en esta tarea ha habido un número elevado de respuestas en blanco (15 alumnos del Grupo 2 y 2 alumnos del Grupo 1), se trata de un problema que discrimina entre los dos grupos de alumnos. Como ejemplo de representación utilizada por los alumnos (Figura 3), se puede ver la resolución de un alumno del Grupo 1, predominantemente simbólica-numérica, y la resolución de un alumno del Grupo 2, que recurre a diferentes representaciones, ambas consideradas parcialmente correctas. Este desempeño del Grupo 2 es de una alumna con un rendimiento elevado tras tener muy buenas calificaciones en el área de Matemáticas.
Fuente: Elaboración propia (2020)
Figura 3 Ejemplos de representaciones usadas por un alumno del Grupo 1 y por una alumna de Grupo 2
La última de las variables analizadas para la PRPM2 ha sido el tipo de estrategias de resolución de problemas utilizadas (Tabla 8).
Tabla 8 Frecuencias según el tipo de estrategias utilizadas en la PCM2
(Fuente: Elaboración propia (2020)
En las tareas 2 y 4 se verifica una diferencia entre los dos grupos. En la tarea 2 un mayor número de alumnos del Grupo 2 elabora una versión más simple del problema para proceder a su solución (7 alumnos por ninguno del Grupo 1), por ejemplo. En la Figura 4 se presenta la resolución a partir de una versión más simple en alumnos del Grupo 2.

Fuente: Elaboración propia (2020)
Figura 4 Resolución de la tarea 2 a partir de una versión más simple por un alumno del Grupo 2
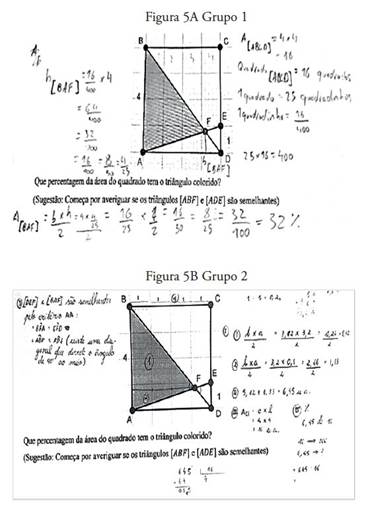
Con relación a la tarea 4, han aparecido diferencias derivadas de la estrategia de patrones y conjeturas (20 alumnos del Grupo 1 y 16 alumnos del Grupo 2), como se ejemplifica en las respuestas dadas por un alumno del Grupo 1 y otro del Grupo 2 (Figura 5). En esta tarea, un mayor número de alumnos del Grupo 2 no presenta cualquier tipo de estrategia (15 alumnos del Grupo 2 contra 2 alumnos del Grupo 1), es decir, el ejercicio ha aparecido en blanco o bien incorrecto y la estrategia utilizada no puede incluirse en ninguno de los tipos de estrategias considerados.
Discusión
Los alumnos y alumnas con altas capacidades intelectuales se diferencian de sus compañeros por una serie de características que les hacen singulares, caso de capacidad cognitiva y adquisición de aprendizajes (Almeida et al., 2016; Tourón, 2019). El estudio de esta singularidad, en este caso para la matemática, ha sido el objetivo de la presente investigación. Se ha buscado analizar la existencia de diferencias entre dos grupos de escolares, identificados o no con altas capacidades intelectuales, en pruebas de resolución de problemas de acuerdo a su edad y teniendo presente el abordaje del problema en cuanto a raciocinio, tipo de representación y estrategia utilizadas.
Con los ítems seleccionados para cada una de las pruebas, gracias a la colaboración de cinco expertos en la materia, se ha buscado una utilidad práctica y diagnóstica con vistas a conocer características distintivas de los escolares con mayores potencialidades, en este caso para la resolución de problemas. Los resultados sugieren que los alumnos con características de superdotación utilizan procedimientos de resolución de problemas diferentes, y más avanzados, a los alumnos de buen rendimiento de acuerdo a los elementos evaluados en cada uno de los problemas utilizados. Además, tras el análisis de las tareas, producciones como las señaladas en el apartado anterior, se han observado otras características como una mayor flexibilidad y organización en sus algoritmos, desarrollo de razonamientos matemáticos originales, utilización de formas de expresión más elaboradas, estructuración avanzada en los cálculos, generalización y transferencia de estrategias ya aprendidas, clarificación en la ejecución de procedimientos a pesar de su complejidad o facilidad en el manejo de distintos sistemas de representación, características distintivas de los escolares con mayor potencialidad para las Matemáticas (Greenes, 1981, 1997).
Fuente: Elaboración propia (2020)
Figura 5 Estrategia de patrones y conjeturas usada por alumnos del Grupo 1 y Grupo 2
Las dos pruebas aplicadas han contado con problemas con distintos niveles de dificultad. En la prueba para alumnos de 2º de enseñanza básica, la puntuación total alcanzada ha sido superior en aquellos escolares detectados con alta capacidad, 4.33 (DT = 2.30) frente a 3.25 (DT = 2.38), observándose diferencias estadísticamente significativas en el ítem 3 o tarea de producción, p <. 05.
También indicar que en el ítem 4 los no detectados con capacidad superior obtienen una puntuación media superior, 1.05 (DT = 1.00) y .89 (DT = 1.02), respectivamente. El principal tipo de raciocinio utilizado por los escolares ha sido el analítico, aunque en el caso de los de capacidad superior sus resoluciones han sido más avanzadas. Estos datos corroboran con otras investigaciones que denotan estrategias más sofisticadas aplicadas por los escolares superdotados, comparativamente a su grupo de pares no identificados con alta capacidad (Geary & Brown, 1991). El tipo de representación más utilizada por ambos grupos de escolares ha sido la simbólica-numérica, siendo de mayor complejidad las realizadas por los escolares más capaces. En cuanto al tipo de estrategias utilizadas, los escolares de uno y otro centro las han utilizado indistintamente, no apareciendo diferenciación entre ellos.
En la otra prueba de resolución de problemas, alumnado de 3º ciclo de enseñanza básica, la puntuación total alcanzada ha sido más elevada para el alumnado detectado con superdotación, 3.95 (DT = 1.36) frente a 2.69 (DT = 1.86), mostrando significación estadística en el ítem 4 o tarea de comprensión, p <. 05, reactivo en el que los escolares no identificados obtienen una puntuación media superior, .78 (DT = .43) y .47 (DT = .51) respectivamente. Ya en el estudio de Kurnaz (2018) se verifica un desempeño superior en tareas matemáticas de aquellos alumnos con altas capacidades, que destacan en los raciocinios presentados y en la resolución de problemas. Pero, de acuerdo con el tipo de raciocinio, en nuestra investigación, no han aparecido diferencias entre los dos grupos. En relación con el tipo de representación, la de tipo simbólica-numérica ha sido la más utilizada por ambos grupos de escolares, siendo más completas las de aquellos escolares más capaces. En el análisis de las estrategias manejadas, en el ítem 2 los alumnos no diagnosticados con superdotación han utilizado mayormente la estrategia de elaborar una versión más simple del problema y de este grupo ha aparecido un número más elevado de alumnos que no han utilizado ninguna estrategia. Las diferencias para el ítem 4 se han debido al uso mayoritario por parte de los escolares con altas capacidades de la estrategia de patrones y conjeturas y, además, ha aparecido un número elevado de alumnos no identificados que no han manejado ninguna estrategia para este ítem.
Conclusiones
La presente investigación ha permitido la observación de diferencias en la resolución de problemas entre escolares identificados o no con superdotación. Las producciones y estrategias utilizadas por los primeros han sido más avanzadas. Otras investigaciones han tomado el rendimiento académico para las Matemáticas como criterio para la diferenciación entre escolares en la resolución de problemas, mostrando diferencias entre el alumnado en los subprocesos utilizados en la planificación y en el uso de estrategias de representación de la información, siendo estas más evidentes conforme la dificultad de las tareas aumentaba (García et al., 2016).
El alumnado con mayores potencialidades, sea atendiendo a criterio de capacidad superior o rendimiento excelente para el área de Matemáticas, muestran formas de ejecución diferenciadas y más sofisticadas que el resto de escolares en la resolución de problemas. En esta investigación se ha observado el manejo, de forma preferente por parte de ambos grupos de alumnos, del raciocinio de tipo analítico, la resolución de problemas mediante representaciones simbólicas y la utilización de la estrategia de patrones y conjeturas para el abordaje del problema. Esto habrá que ser tenido en cuenta en sus procesos de enseñanza y aprendizaje para el área de Matemáticas.
La alfabetización matemática exige conocer el capital humano existente en las aulas, más si cabe en un mundo tan centrado en la tecnología como es el actual, en el que las situaciones cotidianas cambian de forma vertiginosa y ello demanda procesos de innovación constantes. La construcción de estrategias de resolución de problemas personalizadas es una demanda y necesidad inexorable. Todo ello exige una actitud activa y participativa por parte de los alumnos, con actividades que supongan desafíos con amplia aplicabilidad a los entornos naturales de los sujetos. La diferenciación entre alumnos y la individualización de los procesos de enseñanza y aprendizaje, a través del desarrollo de actividades con distintos niveles de dificultad como las utilizadas en esta investigación, suponen un reto para los sistemas educativos.
En esta labor de comprender la individualidad de cada alumno para el aprendizaje matemático, en futuras investigaciones tomaremos en consideración distintas variables que pueden tener incidencia como son el nivel de atención o el ritmo de ejecución en el abordaje de las tareas (Cueli, Areces, García, Alves, & González-Castro, 2020), valorando la posibilidad de influencia de déficits en la velocidad de procesamiento para las Matemáticas (Cirino, Fuchs, Elias, Power, & Schumacher, 2015), aspectos todos ellos fundamentales en la resolución de un problema. Para ello, será necesario la ampliación de la muestra de participantes con vistas a garantizar suficiencia y representatividad de los resultados alcanzados.
Por último, hemos de señalar la importancia del profesorado en los procesos de educación matemática. El docente deberá indagar e investigar con su grupo de escolares para conocer cómo procesan y resuelven los problemas en esta disciplina. Involucrar al alumnado en este autoconocimiento ejecutivo mejora el aprendizaje de las Matemáticas (Boaler, 2016; Hattie, Fisher, & Frey, 2017).