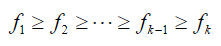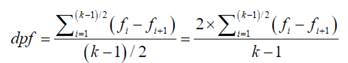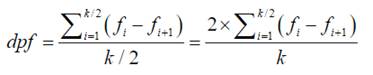El concepto de asimetría en estadística fue introducido por Karl Pearson en el desarrollo de su sistema de 12 distribuciones continuas a finales del siglo XIX. La asimetría y la curtosis como parámetros de forma junto con un parámetro de localización y otro de escala permiten definir las distintas distribuciones de Pearson (Provost et al., 2020). Más allá de las distribuciones continuas, el concepto se generalizó a distribuciones discretas y, de este modo, hoy en día se aplica tanto a variables cuantitativas continuas como cuantitativas discretas y ordinales (Weiss, 2020).
La asimetría se puede ver como una propiedad de la forma de la distribución al ser representada por medio de un diagrama de barras, en el caso de una variable ordinal o cuantitativa discreta con pocos valores (distribución discreta), o por medio de un histograma, en el caso de una variable cuantitativa continua (distribución continua) o discreta con muchos valores (distribución discreta). Como eje de simetría para dividir la distribución en dos partes, se toma una medida de tendencia central, como la media aritmética, mediana, moda o rango medio. Si ambas partes de la distribución son iguales, es decir, una es el reflejo de la otra, hay simetría. Si ambas partes son diferentes, hay asimetría (Mishra et al., 2019). Por ejemplo, si se toma como eje de simetría la media aritmética (µ), una distribución tendría simetría si , donde f (x) es la función de masa de probabilidad en una distribución discreta o la función de densidad en una distribución continua (Cole y Altman, 2017).
Las medidas de asimetría relativas (libres de unidad de medida o libres de los parámetros de localización y escala) se definen como cocientes, proporciones o promedios centrados en 0 (Altinay, 2016). El valor de 0 indica simetría y, en una distribución unimodal continua, refleja que los dos hombros y las dos colas a ambos lados del eje de simetría son idénticos, esto es, un lado es el reflejo del otro (Figura 1). Un valor positivo en la medida de asimetría suele indicar que la cola derecha es más larga que la izquierda, lo que provoca que la media aritmética se vea desplazada hacia la derecha y haya menos valores por encima de la media aritmética que por debajo. En las distribuciones unimodales continuas con asimetría positiva, la moda (pico) queda por debajo de la mediana y la mediana por debajo de la media aritmética (Figura 1). No obstante, su generalización a otros tipos de distribución depende de cuan pesadas o ligeras sean las colas. Así, una cola acortada en un extremo puede compensar una cola alargada en el otro y surgir simetría (valor nulo) cuando ambas partes de la distribución son dispares.
En distribuciones unimodales continuas, un valor negativo en la medida de asimetría muestra que la cola izquierda es más larga que la derecha, lo que ocasiona que la media aritmética se vea desplazada hacia la izquierda y que haya menos casos por debajo de la media aritmética que por encima (Figura 1). En estas distribuciones con asimetría negativa, la moda (pico) queda por encima de la mediana y la mediana por encima de la media aritmética (Sarka, 2021). Esta regularidad se cumple bien en las distribuciones continuas unimodales, pero en las distribuciones discretas tiene muchos contraejemplos (Singh, Gewali, y Khatiwada, 2019), de ahí que es muy importante representar la distribución por medio de un diagrama de barras o un histograma cuando se evalúa la simetría.
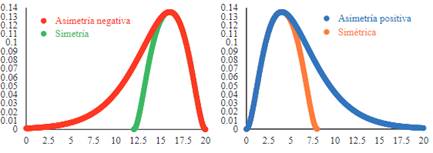
Figura 1 Funciones de densidad que muestran dos ejemplos de curvas asimétricas y la correspondiente curva simétrica de cuatro variables cuantitativas continuas
Existen varias medidas de asimetría relativas (Gupta & Kapoor, 2020; Versluis, 2017). Unas se basan en momentos centrales o cumulantes de tercer orden estandarizados, como el coeficiente √β1 (poblacional) o √b1 (muestral) de Pearson (1895) y el coeficiente γ1 (poblacional) y g1 (muestral) de Fisher (1930). Otras están basadas en cuantiles, como el coeficiente intercuartílico de Bowley (1901) y el percentílico de Kelley (1947). Además, existen unas terceras medidas mixtas que se basan en momentos y cuantiles, como la distancia orientada (con signo) y estandarizada de la media aritmética a la moda (Pearson, 1894) o a la mediana (Pearson, 1895), la distancia dirigida y estandarizada del semirrango a la moda, mediana o media aritmética (Altinay, 2016) o el área de asimetría de Singh et al. (2019). Todas ellas pueden tomar un valor negativo, nulo o positivo, y las medidas de Bowley (1901), Kelley (1947), Altinay (2016) y Singh et al. (2019) están limitadas al rango entre −1 y 1. También hay medidas de asimetría absolutas, como el índice de Kelley (1923).
La propiedad de la asimetría no se estudia en la descripción de una variable cualitativa, aunque sí en la relación entre dos variables cualitativas a partir de una tabla de contingencia cuadrada de datos correlacionados (Bowker, 1948; Fagerland, Lydersen y Laake, 2017). Cabría preguntarse si es posible definir un concepto de asimetría para describir una variable cualitativa y desarrollar una medida para su cuantificación. Retomando esta pregunta, el presente estudio tiene como objetivos: 1) definir un concepto de asimetría unidimensional para variables cualitativas y una medida para dicho concepto, 2) mostrar su validez y 3) generar unas normas orientativas de interpretación.
Método
Para el primer objetivo de definir asimetría cualitativa y una medición de la misma, se emplearon definiciones, argumentaciones y estas se expresaron en términos algebraicos. De aquí surge el estadístico diferencia promedio de frecuencia entre pares de categorías cualitativas ordenadas por homogeneidad o proximidad de frecuencia que se denota por dpf.
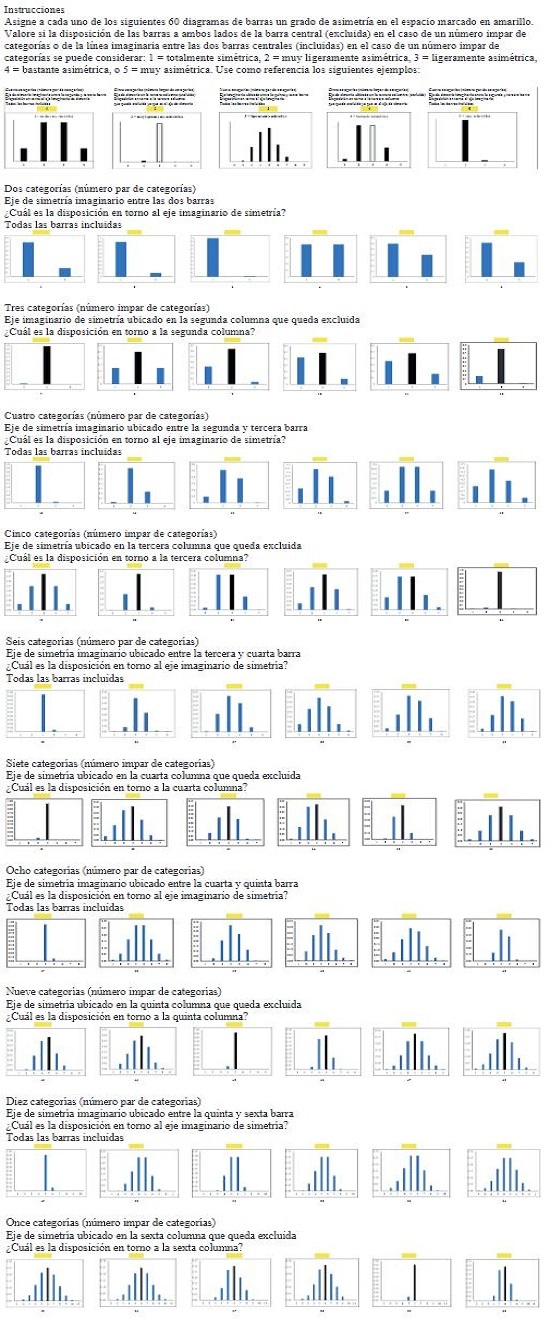
Para el segundo objetivo de mostrar la validez de esta medida, se describe el estadístico con distintas variantes de la distribución binomial que permite emular el comportamiento de una variable cualitativa desde el estadístico propuesto. Se hace variar tanto el parámetro n de número de ensayos independientes de 1 (k = 2 categorías cualitativas) a 10 (k = 11 categorías cualitativas) como el parámetro p de probabilidad de éxito en cada ensayo independiente (p = .01, .1, .2, .3, .4 y .5). La función de masa de probabilidad de las 60 distribuciones binomiales proporciona la frecuencia relativa de las k (= n + 1) categorías de la variable cualitativa. Se espera simetría con un valor p de .5 y asimetría en los demás casos. La expectativa es que el valor de pdf se aproxime a 1 cuanto más dispares sean las frecuencias o alturas de las barras en orden de simetría a ambos lados de la categoría central (número impar de categorías) o del eje imaginario entre las dos categorías centrales (número par).
La validez de dpf se comprobó por medio de correlaciones. A cinco jueces (profesores de estadística en facultades de psicología con grado de doctor), se les dio una escala para clasificar los 60 diagramas de barras en cinco categorías ordenadas. Se les pidió que evaluaran en cada gráfico la simetría o disparidad entre las barras a los lados de la moda (barra central cuando el número de categorías cualitativas es impar o línea imaginaria entre las dos barras centrales cuando el número de categorías es par). La escala tenía un rango de 1 (disposición de las barras a ambos lados de la moda totalmente simétrica) a 5 (disposición muy asimétrica). El instrumento proporcionado a los jueces vía correo electrónico en un archivo Excel, se puede ver en el Anexo. De este modo, cada diagrama de barras contaba con un orden promedio de asimetría desde los cinco jueces y un valor del estadístico dpf. La correlación entre ambos valores y la correlación entre los jueces se calcularon por el coeficiente de correlación por rangos de Spearman (rS).
Para el tercer objetivo de tener puntos de corte de asimetría orientativos, se simularon 20 000 muestras de tamaños 20, 40, 100, 200, 500 y 1000 extraídas de una distribución binomial con parámetro n (n+1 categorías cualitativas) con valores de 1 (2 categorías) a 10 (11 categorías) y parámetro p (probabilidad de éxito) = ½ (simetría). Se calcularon los percentiles 50, 80, 90 y 95, así como el intervalo de la media con un nivel de confianza al 95% del estadístico dpf en las 20,000 simulaciones para cada tamaño muestral y número de categorías. Para describir las distribuciones en el muestreo de pdf, también se computó la asimetría (g1 de Fisher) y exceso de curtosis (g2 de Fisher). El análisis de datos se hizo con el Excel versión 2019 para Windows (Microsoft Corporation, 2019) y la simulación con el módulo XLSTAT para Excel (Addinsoft, 2021). Se dan más detalles sobre la simulación en la sección de Resultados.
Resultados
Definición de asimetría cualitativa
Todo concepto de asimetría implica un eje que permite dividir las distribuciones en dos partes. Si una parte con referencia al eje de simetría es reflejo de la otra, se considera que la distribución muestra simetría y la medida de asimetría debe arrojar un valor de 0. Por el contrario, si son distintas, se habla de asimetría, y el valor de la medida de asimetría debe ser distinto de 0. Cuanto más dispares sean los dos lados divididos por el eje de simetría, el valor de la medida de asimetría debe estar más alejado de 0.
En distribuciones aleatorias continuas, se toma como eje de simetría una medida de tendencia central, como la media aritmética, mediana, moda o rango medio. En el caso de las variables cualitativas, la única opción sería la moda, esto es, la categoría nominal con mayor frecuencia en la muestra. No obstante, la moda no siempre es única. Puede haber dos categorías modales (distribución bimodal), tres o más categorías modales (distribución multimodal) o ninguna (distribución uniforme). Consecuentemente, si se adopta la moda como eje de simetría, el concepto solo podría aplicarse a las distribuciones unimodales y no ser universal.
Si las categorías de una variable en escala nominal se representan por números, estos carecen de cualquier propiedad algebraica. Perfectamente, las categorías se pueden identificar por letras, palabras o símbolos no numéricos para evidenciar el hecho de que representan las opciones de clasificación dentro de un sistema inclusivo (todo elemento de la población se puede clasificar) y exhaustivo (en una sola categoría) y no una medición en sentido estricto (determinación objetiva de cuantas veces la característica medida del objeto es la unidad de medida consensuada por expertos). La única cuantificación que admiten las variables cualitativas es el conteo de las veces en que aparece cada una de sus categorías en la muestra o la población, esto es, la frecuencia o probabilidad de cada categoría. Así, desde su frecuencia relativa o probabilidad, se abre una posibilidad de transformación. Las categorías cualitativas de la variable se pueden transformar en categorías ordenadas. De este modo, se puede crear una métrica ordinal de frecuencia.
Ante todo, la asimetría es una propiedad de la forma de una distribución. Al elaborar el diagrama de barras para estudiar la asimetría en variables cualitativas, no se procede a disponer la secuencia de categorías (ordenadas por frecuencia) en orden ascendente, como es lo estipulado, ya que aparecería una forma de escalera propia de una función monótona creciente, sino que se intenta crear una forma más o menos triangular o trapezoide. Si el número de categorías k es impar, se ubica la categoría de mayor frecuencia (categoría modal) o una de las categorías de frecuencia máxima, elegida al azar, en el centro. Tras emparejar las restantes categorías por homogeneidad o proximidad de frecuencia, estos pares se disponen en orden descendente a ambos lados de la moda. La categoría con frecuencia más alta de cada par se pone a la izquierda y la categoría con la frecuencia más baja del par se pone a la derecha. El par con las frecuencias más altas será el más próximo a la categoría central y el par con las frecuencias más bajas será el que se encuentre más alejado de la categoría central. Si el número de categorías es par, se ubican en el centro el par con las frecuencias más altas y se procede del mismo modo. Si solo hay dos categorías, se puede ubicar en primer orden la más alta y en segundo orden la más baja.
La distribución se puede considerar simétrica, si las dos partes a ambos lados de la categoría de máxima frecuencia ubicada en el centro (número impar de categorías) o de la línea imaginaria perpendicular al eje de abscisas entre las dos categorías centrales de mayor frecuencia (número par de categorías) son iguales. Por el contrario, hay asimetría si son disimilares. A este concepto se le denomina asimetría cualitativa.
Propuesta de una medida de asimetría cualitativa
¿Cómo medir si hay o no similaridad o simetría entre las dos partes de la distribución? Se propone usar la diferencia promedio de frecuencia entre las categorías cualitativas emparejadas por homogeneidad o proximidad de frecuencia. Esta medida no requiere la existencia de una moda única, incluso aplica con una distribución uniforme, cuya forma en el diagrama de barras no es trapezoide, sino rectangular.
A continuación, se expresa la propuesta en términos algebraicos. Sea X una variable cualitativa con un número de k categorías nominales y cada una de ellas con frecuencia relativa i. Las frecuencias se ordenan en sentido descendente, esto es, de las más altas a las más bajas.
Si k es impar, la categoría con la frecuencia modal o la categoría de frecuencia máxima que se ubicó en el centro del diagrama de barra (1), se excluye del emparejamiento de frecuencias. Se emparejan las restantes frecuencias: 2 es igual o inmediatamente mayor que 3, 4 es igual o inmediatamente mayor que 5, , k-1 es igual o inmediatamente mayor que k. Se restan los (k−1)/2 pares de frecuencias similares o más próximas, se suman las diferencias y se dividen por el número de diferencias sumadas: (k−1)/2. De este modo, se obtiene la diferencia promedio de frecuencia entre las categorías cualitativas emparejadas por homogeneidad o proximidad de frecuencia que se denota por dpf.
Si k es par, se emparejan las frecuencias: 1 es igual o inmediatamente mayor que 2, 3 es igual o inmediatamente mayor que 4, . k-1 es igual o inmediatamente mayor que k. Se restan los k/2 pares de frecuencias similares o más próximas, se suman las diferencias y se dividen por el número de diferencias sumadas (k/2), con lo que se obtiene dpf.
El estadístico dpf está acotado de 0 a 1. Un valor de 0 indica simetría, que puede corresponder a un perfil triangular (distribución unimodal), trapezoide (distribución bi o multimodal) o rectangular (distribución uniforme). Un valor de 1 representa la máxima asimetría y se alcanza con la distribución de una variable aleatoria discreta constante en la que un valor concentra toda la probabilidad o frecuencia (distribución Bernoulli de parámetro p = 1).
Comportamiento y validez del estadístico dpf
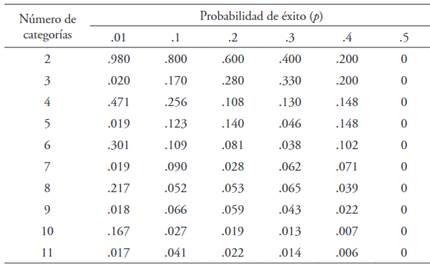
Para estudiar el comportamiento del estadístico dpf, se crearon 60 distribuciones cualitativas. El número de categorías nominales en estas variables osciló de 2 a 11. Las frecuencias de las categorías se generaron a partir de las funciones de masa de probabilidad de 60 distribuciones binomiales . La probabilidad del número de éxitos () pasó a ser la frecuencia relativa de la categoría nominal. Para lograr los grados variables de asimetría, se dieron seis valores diferentes a las probabilidades de éxito: .01 (probabilidad muy baja), .1, .2, .3, .4 y .5 (probabilidad media). Se obvió la otra mitad de probabilidades (.6, .7, .8, .9 y .99), ya que el índice dpf siempre es positivo y daría el mismo resultado, como se puede apreciar en la Tabla 1 y Figura 2.
Tabla 1.Generación de dos variables con 10 categorías nominales, una desde una distribución binomial de parámetros n = 9 y p = .3 y otra desde una distribución binomial de parámetros n = 9 y p = .7, y ordenamiento de sus categorías para calcular dpf y el diagrama de barras
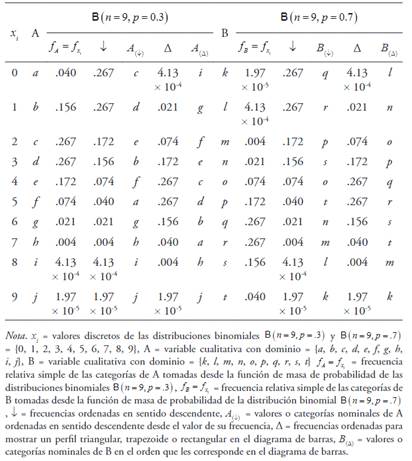
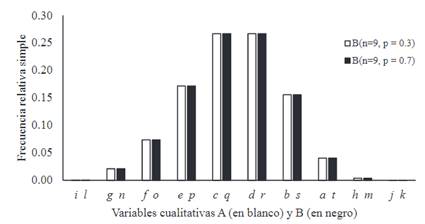
Figura 2 Diagrama de barras para valorar la asimetría cualitativa de las variables cualitativas A y B con 10 categorías, cuyas frecuencias corresponden a las probabilidades de una distribucional binomial y , respectivamente.
De las 60 distribuciones (Tabla 2), 10 fueron simétricas (p = .5) y el resto fueron asimétricas en diferente grado (p ≠ .5). El hecho de que el valor de p se aproxime a uno no implica necesariamente que la asimetría sea mayor, ya que depende de cuan dispares sean las frecuencias con respecto al eje de simetría (incluido con k par y excluido con k impar).
Tabla 2 Generación de distribuciones cualitativas de 2 a 11 categorías y asimetría variable desde la distribución binomial
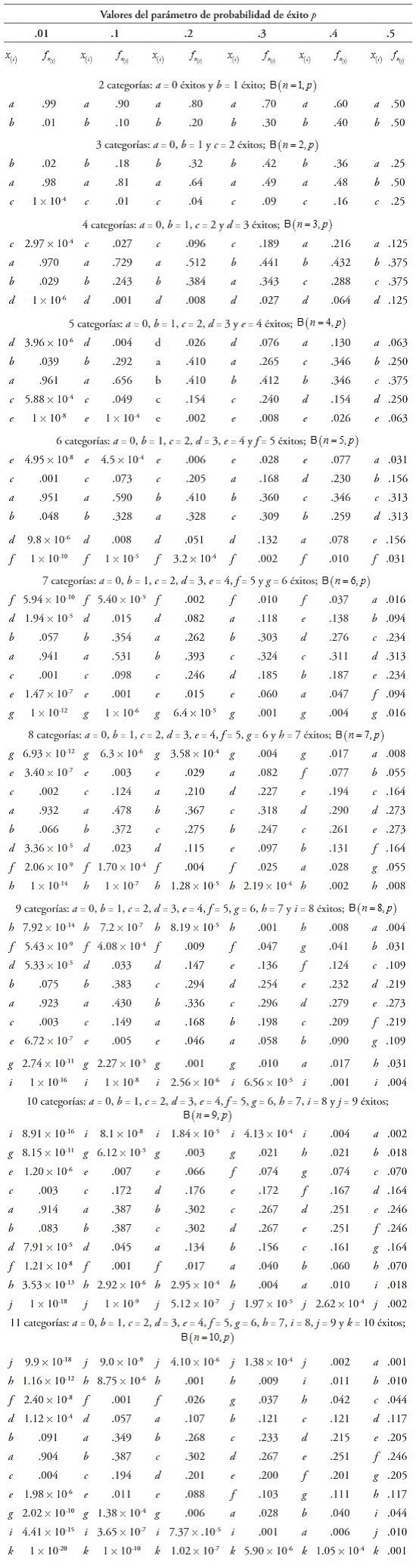
Se observó que, cuando p = .5, dfp toma un valor nulo con cualquier número de categorías (k de 2 a 11), ya que las frecuencias son totalmente simétricas con respecto al eje de simetría. Con un valor de p extremo de .01, dfp alcanza los valores más altos cuando el número de categorías es par y, en esta condición, dpf es más alto cuanto menor es el número de categorías, ya que hay mucha diferencia entre las dos categorías centrales. No obstante, si k es impar, dpf presenta un valor próximo a 0, ya que la categoría modal excluida (eje de simetría) concentra casi toda la probabilidad y separa las restantes categorías (de muy baja frecuencia) en dos partes muy semejantes, resultando un perfil simétrico. Con una probabilidad de .1, este patrón es más tenue; con un número par de categorías el valor de dpf es más alto que con un número impar; no obstante, en ambos casos dpf disminuye a medida que el número de categorías aumenta. El hecho de que haya solo dos categorías marca el máximo de la asimetría para todos los niveles de probabilidad. Precisamente, con un valor de p = .01, la distribución se aproxima mucho a una variable aleatoria constante y dpf es igual a .98 (Tablas 2 y 3). Así, el comportamiento del estadístico se ajustó bien a las expectativas.
A cinco jueces se le dio una escala con cinco categorías ordenadas para clasificar los 60 diagramas de barras. El criterio de ordenación era si la disposición de las barras a ambos lados de la barra central (excluida) en el caso de un número impar de categorías o de la línea imaginaria entre las dos barras centrales (incluidas) en el caso de un número par de categorías se puede considerar: 1 = “disposición totalmente simétrica”, 2 = “muy ligeramente asimétrica”, 3 = “ligeramente asimétrica”, 4 = “bastante asimétrica” y 5 = “muy asimétrica” (Anexo). Conforme al resultado previo, la correlación entre la puntuación promedio de asimetría de los cinco jueces y dpf fue muy alta, r S = .87, IC al 95%: [.74, 1]. A su vez, la correlación entre los cinco jueces varió de .44 a .74 con un promedio entre las 10 correlaciones de r̄ S = .63, IC al 95% [.54, .65].
Valores críticos orientativos de asimetría para dpf
Los valores críticos orientativos para rechazar la hipótesis nula de simetría (percentiles 90, 95 o 99) se obtuvieron por medio de simulación Monte Carlo. Se ejecutaron 20,000 extracciones. Las simulaciones se hicieron para muestras con seis tamaños distintos: 20, 40, 100, 200, 500 y 1000. Se partió de una distribución binomial . La probabilidad de éxito (parámetro p) se fijó en .5 para tener simetría perfecta a nivel poblacional y, consecuentemente, un estadístico dpf nulo. El número de categorías (k) de la variable cualitativa A se hizo corresponder al número de éxitos (x) de la variable binomial X, con lo que el número de ensayos independientes (parámetro n) es k - 1. Se consideraron de 2 a 11 categorías nominales con incremento de 1.
Primero, se computó la función de masa de probabilidad de la distribución binomial . Segundo, se multiplicaron las k probabilidades obtenidas por el tamaño muestral n y se redondearon al entero más próximo (). La suma necesariamente debía ser n y conservarse la perfecta simetría desde la categoría modal excluida (k impar) o desde las dos categorías modales incluidas (k par). En caso de que faltara un valor al sumar las k frecuencias absolutas, se agregaba 1 a la frecuencia absoluta de la categoría modal. Por el contrario, si sobraba, se le restaba uno a la frecuencia absoluta de la categoría modal. Tercero, se dividió las frecuencias absolutas ni por n. Las frecuencias relativas o probabilidades resultantes, en algunos casos, coincidían con las probabilidades de la distribución binomial y, en otros casos, diferían ligeramente. Cuarto, se definieron las distribuciones de los argumentos del estadístico dpf desde la aproximación de la proporción binomial a la distribución normal. Finalmente, se computó el estadístico dpf que en todos los casos era nulo (variable resultado). A continuación, se muestra un ejemplo de cómo se planteó la simulación: el caso de cuatro categorías nominales y una muestra de tamaño 20 (Tabla 4).
Se generaron un total de 60 simulaciones con reemplazamiento con 20,000 muestras simuladas (6 tamaños muestrales 10 números distintos de categorías nominales). Las Tablas de la 5 a la 9 permiten apreciar que la distribución del estadístico dpf en todos los casos presentó asimetría positiva () y leptocurtosis (), alejándose de una distribución normal. La cola derecha fue más larga que la izquierda y hubo un desplazamiento importante de la masa de probabilidad de la zona de los hombros hacia la cola derecha (Figura 3). Su variabilidad fue alta (.70 ≤ CV < 1) y alcanzó a ser muy alta con cuatro, cinco, diez y once categorías nominales (CV > 1).
Tabla 5 Estadísticos descriptivos y normas para la distribución del estadístico dpf ante una distribución simétrica (p = .5) con dos y tres categorías para tamaños muestrales de 20, 40, 100, 200, 500 y 1000 participantes
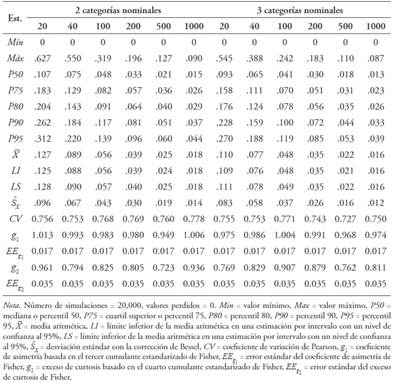
Tabla 6 Estadísticos descriptivos y normas para la distribución del estadístico dpf ante una distribución simétrica (p = .5) con cuatro y cinco categorías para tamaños muestrales de 20, 40, 100, 200, 500 y 1000 participantes
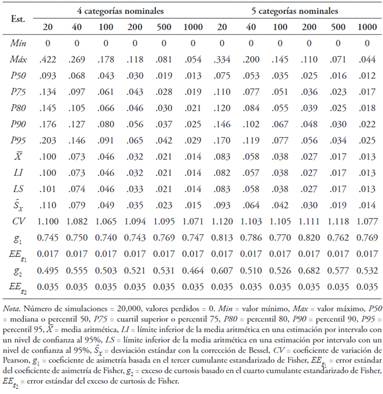
Tabla 7 Estadísticos descriptivos y normas para la distribución del estadístico dpf ante una distribución simétrica (p = .5) con seis y siete categorías para tamaños muestrales de 20, 40, 100, 200, 500 y 1000 participantes
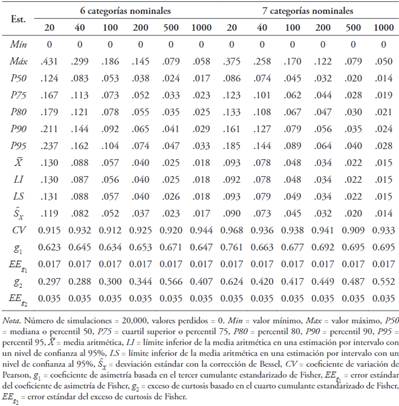
Tabla 8 Estadísticos descriptivos y normas para la distribución del estadístico dpf ante una distribución simétrica (p = .5) con ocho y nueve categorías para tamaños muestrales de 20, 40, 100, 200, 500 y 1000 participantes
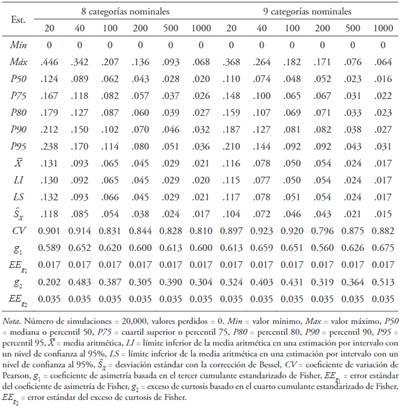
Tabla 9 Estadísticos descriptivos y normas para la distribución del estadístico dpf ante una distribución simétrica (p = .5) con diez categorías para tamaños muestrales de 20, 40, 100, 200, 500 y 1000 participantes
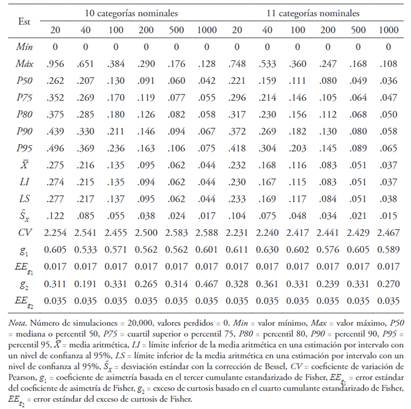
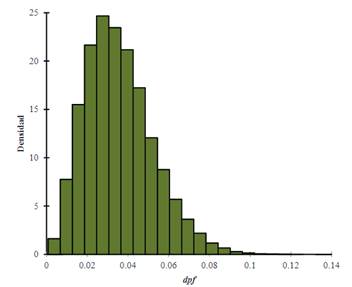
Figura 3 Histograma de la distribución de dpf para seis categorías nominales y un tamaño muestral de 1000
La mediana de los valores del percentil 95 (punto de corte más usual), generados para seis tamaños muestrales y 10 números distintos de categorías, fue de .09. Al estudiar el comportamiento del percentil 95 desde las Tablas 6 a 10, se observó que existe una correlación lineal inversa muy alta entre los valores del percentil 95 y el tamaño muestral (r S = -.90). La relación entre los valores del percentil 95 y el número de categorías no fue lineal, sino que tuvo una forma de U (R 2 = .55 para un modelo cuadrático). A su vez, los valores del percentil 95 fueron ligeramente más altos cuando el número de categorías fue par (Mdn = .11) que cuando fue impar (Mdn = .09), aunque sin diferencia significativa (U = 398.5, Z = -.76, p = .446).
Discusión
Las variables cualitativas han recibido una amplia atención por parte de la estadística tanto descriptiva como inferencial. Se cuenta con tablas, gráficas, medidas de tendencia central, variación y asociación, pruebas de bondad de ajuste y técnicas de predicción, clasificación y reducción de dimensiones. A su vez, se ha estudiado la simetría en tablas de contingencia, tomando como eje de simetría la diagonal principal (frecuencias conjuntas de acuerdo), pero se ha ignorado el aspecto de la asimetría y el apuntamiento unidimensionales.
Para hablar de asimetría se requiere tener un eje a partir del cual se pueda evaluar si una parte de la distribución es igual a la otra parte (simetría) o es dispar (asimetría). En un principio, la opción natural parece la moda, pues es la medida de tendencia central de una variable cualitativa. No obstante, es una medida problemática, ya que puede ser múltiple, incluso no existir. Aparte, está el problema del orden de los datos. Las categorías nominales no poseen información intrínseca para su ordenación. Este problema se supera tomando una información extrínseca que sí tienen las categorías nominales, como es su frecuencia. La frecuencia permite un ordenamiento de las categorías. En este caso, no interesa simplemente un ordenamiento ascendente o descendente, pues no facilitaría observar gráficamente la simetría. Interesa un ordenamiento que lleve a un perfil triangular, si la moda es única; trapezoide, si hay dos o múltiples modas; o rectangular, si no hay moda. Se ubica en el centro una categoría de frecuencia máxima cuando k es impar o dos de las categorías con frecuencia máxima cuando es k par. Emparejadas las categorías por proximidad de frecuencia, se ubican los miembros de cada par a izquierda y a derecha de este centro, a la izquierda la categoría con más frecuencia del par y a la derecha la categoría con menos frecuencia del par. Los pares con frecuencias más altas quedan más cerca del centro y los pares con las frecuencias más bajas aparecen más alejados del centro. De este modo, el diagrama de barras permite visualizar si hay simetría o no.
Una cuantificación natural y muy sencilla de cálculo es promediar la diferencia entre las frecuencias de las categorías dispuestas en simetría. Cuando hay simetría, el valor de este promedio es cero. Cuando hay asimetría, el promedio se aleja de cero hasta alcanzar un máximo de 1. Esta medida nunca es negativa. Su máximo se encuentra con una variable aleatoria constante dicotómica. En esta distribución, una categoría concentra toda la frecuencia o probabilidad y la otra categoría tiene una frecuencia o probabilidad nula. El mínimo de 0 aparece con distribuciones como la uniforme discreta y aquellas que emulan a la Bernoulli o binomial con parámetro p = .5 o a la triangular discreta simétrica.
Los datos presentados muestran que el comportamiento del estadístico se ajusta al patrón esperado: bajar hacia cero cuando hay simetría con respecto al eje situado en la categoría central (k par) o el eje imaginario entre las dos categorías centrales (k impar) y subir hacia 1 cuanto más dispares son ambas partes. Este ajuste es constatado por la correlación entre el índice y la puntuación promedio de asimetría de los cinco jueces. La correlación es muy alta y, cuando se estima por intervalo con un nivel de confianza al 95%, incluye el 1. A su vez, la correlación entre los cinco jueces es alta, lo que indica que es una cualidad fácil de valorar visualmente por expertos. Para estudiar este comportamiento y obtener las gráficas evaluadas en grado de asimetría por los cinco jueces se acudió a la distribución binomial, al ser una variable discreta que puede variar de asimetría extrema negativa a asimetría extrema positiva, pasando por un punto medio de simetría.
También se usó la distribución binomial con parámetro p = .5 para estudiar la distribución del estadístico y obtener unos puntos de corte sugerentes de asimetría. La ventaja de esta distribución es que el dominio de la variable binomial (de 0 a n) permiten establecer un paralelismo con el número de categorías de una variable nominal (de 1 a k = n+1). Aparte esta distribución permite definir las distribuciones de los componentes del estadístico como proporciones binomiales y usar la aproximación a la distribución normal, lo que facilita la simulación de datos. Finalmente, la probabilidad de éxito de un medio garantiza la simetría perfecta y el valor nulo del estadístico a nivel poblacional.
Se puede tomar como punto de corte para asimetría el percentil 95. Su mediana es .09 que constituiría la referencia más generalizada de punto de corte. No obstante, el valor del punto de corte es más alto cuanto menor es el tamaño muestral, ya que existe una relación lineal inversa muy alta entre el valor del percentil 95 y el tamaño muestral. A su vez, los valores más altos del percentil 95 aparecen con tamaños muestrales pequeños y grandes y los más bajos con las categorías centrales, alcanzándose el mínimo con cinco categorías, ya que existe una relación no lineal entre el percentil 95 y el número de categorías. También existe una tendencia a que el valor del percentil 95 sea más alto cuando el número de categorías es par que cuando es impar, aunque en última instancia no es significativa. Desde este patrón, se puede deducir que el punto de corte mínimo aparece con cinco categorías nominales y un tamaño de muestra de 1000 (P95 = .03) y el máximo con 10 categorías nominales y un tamaño muestral de 20 (P95 = .47).
Una limitación del estudio es haber usado exclusivamente la distribución binomial. Otra opción más compleja para simular datos y obtener los puntos de corte sería una distribución triangular discreta simétrica. Además, como la distribución binomial, la distribución triangular puede ser asimétrica en diversos grados, lo que posibilitaría constatar el adecuado comportamiento del estadístico dpf y corroborar los presentes resultados. Está distribución tiene tres parámetros: a (mínimo), b (moda), c (máximo) y estos tres parámetros deben cumplir la condición de que a < b < c. En caso de simetría, se pueden redefinir como: Min = 2a < Mo = a + b < Max = 2b. El dominio de una variable X con esta distribución es el conjunto finito= {2a, 2a+1, … 2b-1, 2b}. Así, la cardinalidad del conjunto es: n = b - a + 1 y, como la distribución binomial, permite establecer un paralelismo con el número de categorías nominales.
Se concluye que sí se puede definir un concepto de asimetría para distribuciones de variables cualitativas. El promedio de las diferencias entre las frecuencias en disposición simétrica permite definir un estadístico que oscila de 0 a 1, donde 0 indica simetría y 1 la asimetría máxima. Además, esta disposición permite una valoración visual confiable de la asimetría. Este estadístico es válido al mostrar un comportamiento ajustado a la definición de asimetría cualitativa. Se aproxima a 0 cuanto más simétricas o semejantes son las frecuencias o alturas de las barras equidistantes al eje de simetría y se aproxima a 1 cuanto más dispares son. A su vez, es preciso como indica su correlación muy alta con el promedio de las valoraciones de asimetría de los jueces expertos. La simulación Monte Carlo con base en la distribución binomial con parámetro p = .5, permite obtener unos puntos de corte (percentil 95) sugerentes de asimetría en función del número de categorías nominales y el tamaño muestral. El punto de corte es más alto cuanto menor es el tamaño muestral y con un número pequeño (2 o 3) y grande (< 6) de categorías nominales.
Se sugiere aplicar esta medida de asimetría en la descripción de las distribuciones de variables cualitativas, usar los puntos de corte generados y confirmar los presentes resultados, usando la distribución triangular simétrica. Por otra parte, se incita a desarrollar un concepto, una medida y unos puntos interpretativos de apuntamiento para describir distribuciones de variables cualitativas. La distancia vertical entre la frecuencia de la moda (pico) y el promedio de las frecuencias de las dos categorías inmediatamente adyacentes al centro (hombros) en la disposición triangular, trapezoide o rectangular descrita en este artículo podría ser de utilidad. En el caso de dos categorías, sería la diferencia entre las frecuencias de ambas categorías.