Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Areté
versión impresa ISSN 1016-913X
arete v.19 n.2 Lima 2007
ARTÍCULOS
Matemáticas, unidad sintética y a priori constitutivo
Mathematics, synthetic unity and constitutive a priori
Álvaro Peláez1
1 Universidad Autónoma Metropolitana
RESUMEN
Partiendo del énfasis sobre la idea kantiana de originaria unidad sintética de apercepción como la función básica sobre la cual descansa la producción de todo juicio sintético, en este artículo defiendo la idea de a priori constitutivo de la experiencia bajo la forma de un principio sintético semejante pero esencialmente formal, a saber, el concepto de transformación y grupo de transformaciones. Paralelamente, intento mostrar, también, que Kant se inspiró, para articular su propia concepción, en las matemáticas, especialmente en la geometría sintética.
Palabras clave: Epistemología, Kant, a priori constitutivo, matemáticas.
ABSTRACT
Starting from the emphasis about the kantian idea of the originary synthetic unity of apperception like the basic function on which rest the production of all synthetic judgment, in this paper I defend the idea of constitutive a priori of experience under the form of a similar synthetic principle but essentially formal, namely, the concept of transformation and group of transformations. To the same time, I try to show that Kant himself inspired, for articulate his own position, on mathematics, especially on synthetic geometry.
Key words: Epistemology, Kant, constitutive a priori, mathematics.
Introducción
No cabe duda de que, desde el punto de vista de Kant, conocer un objeto significa que hemos efectuado una unidad sintética en la multiplicidad de la intuición. La tarea fundamental de la Crítica de la razón pura es ahora comprender ese mecanismo y examinarlo en cada una de sus condiciones. Quiere mostrar cómo se engranan las diversas formas fundamentales del conocimiento, la sensación y la intuición pura, las categorías del entendimiento puro y las ideas de la razón pura, y cómo, en su interrelación, determinan la configuración teórica de la realidad. Esta determinación no es derivada del objeto sino que entraña un acto de espontaneidad del entendimiento.
Cuado pasamos de los primeros estadios de la investigación trascendental, de la elucidación de la forma pura de la sensibilidad, y entramos en el ámbito del análisis del entendimiento, Kant nos conduce a la asunción reductiva de que la función fundamental responsable de la síntesis constitutiva de los objetos de experiencia es la originaria unidad sintética de apercepción a través de la síntesis figurativa1. En función de este principio unificador, podemos decir que tanto las intuiciones puras de espacio y tiempo, como los conceptos puros del entendimiento, son diferentes aspectos o manifestaciones de la forma básica de la función sintética unificadora. La originaria unidad sintética de apercepción y la síntesis figurativa constituyen, entonces, para Kant, la actividad creativa fundamental del pensamiento, mediante la cual este genera progresivamente todo objeto de conocimiento, empírico o matemático.
Lo realmente novedoso del punto de vista de Kant es que lo que podríamos llamar la cosmo-imagen del conocimiento teórico no se nos aparece como dada, como un producto terminado que nos es impuesto de algún modo por la naturaleza de las cosas, sino como un resultado de la libre constitución de la mente, que en ningún punto es arbitraria, sino que está enteramente sujeta a leyes. ¿Dónde debemos buscar la clave de esta idea de constitución, fundamental en la epistemología kantiana?
Bien conocida es la importancia que las matemáticas habían adquirido desde el siglo XVI, tanto en la elaboración de la imagen científica, como en la construcción de teorías filosóficas. En mi opinión, la idea de a priori constitutivo fue articulada por Kant sobre la base del modelo de construcción que le ofrecía la geometría, especialmente la geometría sintética. En efecto, podemos ubicar a Kant en una línea de pensadores que rechazaron los métodos analíticos cartesianos y defendieron el método de la geometría antigua como el paradigma de construcción de lo propiamente espacial. Este método fue extendido y aplicado no solo a la geometría sino al resto de las matemáticas y a la teoría general de la definición. Entre los filósofos que adoptaron esta perspectiva encontramos a Hobbes, Spinoza y Leibniz. Lo que estos filósofos pretendían no era meramente importar los métodos geométricos al corazón de la epistemología, sino algo más profundo, a saber, querían mostrarnos que la misma función conceptual que opera en la generación del pensamiento matemático opera en la construcción del conocimiento empírico.
De este modo, parece que debemos buscar la clave de lo a priori constitutivo en la filosofía kantiana en este procedimiento de construcción sintética que hunde sus raíces en la geometría antigua. Asimismo, si interpretamos de esta manera el sentido de lo a priori constitutivo en la filosofía de Kant, esto es, sobre la base de la idea de la función sintética básica, entonces podemos dar sentido a cierta filosofía posterior que hizo énfasis en el papel constitutivo de ciertos principios formales que, a pesar de ser formales, ofician como verdaderos principios de síntesis de los elementos que constituirán la experiencia. Sobre esta base, conjuntamente con una nueva apelación a las matemáticas, podríamos articular una nueva concepción de lo a priori constitutivo.
El propósito de este trabajo es mostrar que, así como en Kant las matemáticas, especialmente la geometría, sirvieron como fuente de inspiración para la articulación de su concepción de lo a priori constitutivo, ellas todavía pueden servirnos para ese propósito. En función de esto, dividiré el presente artículo en tres partes fundamentales: en la primera, contrastaré los métodos analítico y sintético en geometría, centrándome de manera especial en el último; la segunda sección estará dedicada al análisis de las nociones kantianas de unidad sintética de apercepción y síntesis figurativa, bajo la sugerencia de que ambas nociones están inspiradas en los principios básicos de la geometría sintética; por último, en la tercera sección, sugeriré que la función constitutiva básica que Kant articuló sobre el modelo de la geometría sintética puede encontrar una nueva formulación en el concepto matemático de grupo.
1. Geometría sintética y analítica
En geometría hay una antigua distinción entre dos tipos de métodos. Por un lado, está el método que consiste en suponer un resultado deseado que se puede alcanzar; por ejemplo, suponer que hemos tenido éxito en hacer una construcción deseada en el sentido corriente de construcción. Luego, a partir de estas suposiciones, se argumenta hacia atrás, por así decirlo, hacia las condiciones a partir de las cuales la construcción es posible y hacia las maneras en las que se puede realizar. Este método se llama analítico. Algunas veces, ha sido atribuido a Platón, pero no se empleó en gran escala, explícita y sistemáticamente, hasta la geometría analítica de Descartes, cuyo mismo nombre se deriva del método analítico en cuestión. El otro método es el método sintético. Su aplicación consiste en tratar de producir el resultado deseado mediante la efectuación real de construcciones, y, lo que es más importante, dicha construcción procede a partir elementos simples correspondientes a un conjunto fijo de reglas. Aquello que distingue a los dos métodos, por lo tanto, es, de manera general, el hecho de que en el método analítico no se hacen construcciones, mientras que el método sintético se basa en el empleo de construcciones reales.
El paradigma clásico de la utilización del método sintético en geometría se encuentra en los Elementos de Euclides. Estos comienzan con 23 definiciones, en las cuales se definen la mayoría de los términos básicos, cinco postulados y cinco nociones comunes. Los postulados posibilitan que se realicen ciertas construcciones geométricas: unir dos puntos con una línea, trazar un círculo con cualquier radio y con centro en cualquier punto, etc. Las nociones comunes son deducciones permisibles o reglas de inferencia aplicables fuera de las matemáticas: dos cosas que son iguales a una tercera son iguales entre sí, si cantidades iguales se agregan a cantidades iguales, los resultados son iguales, etc.
¿Cuál es la estructura de una proposición en la geometría de Euclides? Primero hay una enunciación de una proposición general. Por ejemplo, en la proposición 20 de los Elementos dice: En todo triángulo dos lados tomados juntos de cualquier manera son mayores que el restante2. Esta parte de la proposición fue llamada πρότάσις. Pero Euclides jamás procede únicamente sobre la base de la enunciación. En cada proposición, indica a continuación la manera en que es posible construir, por así decir, un ejemplar de la figura que se enuncia en la πρότάσις. Esta construcción equivale a una verdadera demostración de la proposición en cuestión. Dice a continuación de la proposición 20: Pues, sea ABΓ un triángulo. Digo que dos lados del triángulo ABΓ tomados juntos de cualquier manera son mayores que el restante, los lados BA, AΓ (mayores que) BΓ, los lados AB, BΓ (mayores que) AΓ, y los lados BG, GA (mayores que) AB3. Esta parte de una proposición euclideana era llamada έκυεσις o exposición (la traducción latina fue expositio).
La exposición o έκυεσις está estrechamente ligada con la parte que sigue, o tercera parte, de una proposición euclideana, la construcción auxiliar. Esta parte era a menudo llamada la preparación u organización (κατασκευή). Consistía en declarar que la figura construida en la exposición tenía que ser completada mediante el trazado de algunas líneas, puntos y círculos adicionales. En nuestro ejemplo, la preparación dice así: Prolónguese por el otro lado BA hasta el punto Δ, y hágase AΔ igual a ΓA y trácese AΓ4.
La construcción era seguida por la άποδειξις o prueba propiamente dicha. En esta no se realizaban más construcciones. Allí tenía lugar una serie de inferencias que concernían a la figura que había sido introducida en la exposición y completada en la construcción auxiliar. Estas inferencias hacían uso de axiomas, proposiciones anteriores, y de las propiedades de la figura que se seguían del modo en que la figura estaba construida.
Después de haber alcanzado la conclusión deseada acerca de la figura particular, Euclides regresaba otra vez a la enunciación general, diciendo, por ejemplo: Por consiguiente, en todo triángulo dos lados tomados juntos de cualquier manera son mayores que el restante5.
De modo que, en la geometría sintética, la actividad fundamental sobre la cual descansa cualquier demostración es la construcción, la cual, tanto entre los sofistas y Platón, como en Euclides mismo, debía proceder a través de la utilización de dos instrumentos fundamentales: regla y compás. Las construcciones con regla y compás implican las siguientes asunciones: (I) cualesquiera dos puntos pueden ser unidos mediante un segmento de línea; (II) cualquier segmento de línea puede ser extendido para formar una línea; y (III) un círculo puede ser trazado con cualquier centro y distancia dada. Estas tres asunciones, usualmente atribuidas a Platón, se corresponden con los primeros tres de los cinco postulados de Euclides. Los dos restantes son: (IV) cualesquiera dos ángulos rectos son iguales; y (V) si una línea m intersecta dos líneas p y q tal que la suma de los ángulos interiores sobre el mismo lado de m es menor a dos ángulos rectos, entonces las líneas p y q se intersectan sobre el lado de m en el cual la suma de los ángulos interiores es menor a dos ángulos rectos.
Estos dos postulados, y especialmente el último, han presentado problemas a los matemáticos. Dado que Euclides evitó usar el quinto postulado hasta que fue necesario en la prueba de la proposición 29 (del libro I), parece razonable asumir que él sintió alguna inseguridad respecto de él. Pero lo que me interesa mostrar aquí es que los cinco postulados de Euclides incluyen asunciones que subyacen a las construcciones con regla y compás.
Este énfasis en las construcciones es también evidente en las primeras tres proposiciones del libro I: Proposición I. Construir un triángulo equilátero sobre una recta finita dada Proposición II. Poner en un punto dado (como extremo) una recta igual a una recta dada Proposición III. Dadas dos rectas desiguales, quitar de la mayor una recta igual a la menor6. Las construcciones de líneas y figuras no son simples recursos materiales con fines didácticos, sino que sirven para establecer su existencia. Los géneros de existencia solo pueden ser claramente aprehendidos cuando son distinguidos claramente unos de otros y limitados a un círculo fijo de contenido. De este modo, cada forma geométrica posee un carácter aislado e invariable.
Ahora bien, como es sabido, la geometría de los siglos XVII y XVIII estuvo profundamente influida por los métodos analíticos. Descartes y Fermat, insatisfechos con los métodos de la geometría sintética, con su dependencia de la intuición, iniciaron un movimiento entre los matemáticos que los llevó a preferir el método de las coordenadas y la fuerza del cálculo para tratar las cuestiones geométricas.
Descartes había llevado las matemáticas al corazón de su filosofía. Su intento de reconstrucción del conocimiento desde cimientos inamovibles lo condujo a buscar un método nuevo para obtener conocimientos seguros y dignos de confianza. Este método era, justamente, el método analítico.
En la antigua Grecia, lo que se sometía a un análisis era una configuración geométrica ejemplificada por una figura. Las diversas partes del análisis iban desde un objeto geométrico hasta otro o quizás desde un número de objetos hasta un número de otros objetos. Las etapas de un objeto geométrico a otro estaban mediadas por su interdependencia dentro del marco del resto de la configuración. Al estudiar tales interdependencias, un analista analizaba la configuración en cuestión casi de manera literal en el significado, propio del sentido común, de separar sus partes. Descartes y sus contemporáneos generalizaron y desarrollaron esta idea de análisis como descomposición de una configuración. En la práctica de los geómetras de la antigua Grecia, estas interrelaciones son, típicamente, equivalencias simples entre las diferentes líneas y ángulos de la figura. Mediante un empleo mayor de métodos algebraicos por parte de los predecesores inmediatos a Descartes, estas interdependencias se tornaron cada vez más flexibles, hasta que, en la geometría analítica de Descartes, cualquier dependencia polinómica pudo ser representada de manera geométrica. De hecho, en su geometría, Descartes hizo mucho hincapié en esta representabilidad algebraica característica de una amplia variedad de diferentes tipos de interdependencias geométricas.
Vale la pena indicar la manera en la que Descartes se expresa sobre esta cuestión. No tenía a su disposición ningún concepto general de función (dependencia funcional); por lo tanto, para referirse a ello, tuvo que hablar de comparaciones. Con todo, su propósito es claro. De hecho, Descartes llega a afirmar que todo conocimiento que no se adquiere por la intuición pura y simple de un objeto aislado se adquiere por la comparación de dos o más objetos entre sí7.
No obstante la profunda influencia de la geometría analítica, la geometría sintética tuvo en los siglos XVII y XVIII sus defensores. El interés en este método geométrico se vio acrecentado por las necesidades de artistas y arquitectos, quienes requerían una técnica y un conjunto de convenciones apropiadas para representar figuras tridimensionales en un plano. Los dos primeros nombres de importancia involucrados en estos desarrollos fueron los de Desargues y Pascal, a los cuales luego se unieron los de Monge, Poncelet y Von Staudt. Desargues y Pascal visualizaron las secciones cónicas (círculo, elipse, parábola, hipérbola) como proyecciones de círculos, descubrieron otras propiedades de las cónicas y prepararon los fundamentos para la geometría proyectiva sintética. Monge hizo contribuciones importantes a la cuestión de los puntos imaginarios, las cuales fueron desarrolladas por Poncelet y Von Staudt8. Lo que es característico de estos nuevos desarrollos en geometría sintética es que los matemáticos implicados en ellos no volvieron al uso primitivo de los diagramas, sino que reinterpretaron su utilidad a la luz de los resultados de exactitud que la geometría analítica había demostrado tener. En efecto, el paso dado por Poncelet consistió en no tomar a un diagrama particular dado como el objeto de estudio de la geometría, sino, antes bien, como un signo complejo cuyos componentes pueden ser operados sin tomar en cuenta las particularidades que se siguen de sus caracteres visualizables, y de allí obtener propiedades generales de las figuras.
Lo que es importante destacar es que, no obstante el creciente nivel de formalización al que la geometría sintética fue conducida, el uso de las construcciones permaneció como su característica fundamental. Un último ejemplo mostrará esto. Permítaseme considerar la construcción del plano proyectivo y del espacio proyectivo de tres dimensiones. Como es sabido, en cualquier sistema lógico son necesarios ciertos elementos indefinidos. En la geometría proyectiva sintética los elementos indefinidos son puntos y líneas. El plano y el espacio proyectivo de tres dimensiones pueden luego ser construidos en base a los postulados de existencia e incidencia9.
-
Postulados de incidencia10:
-
P1. Si A y B son puntos distintos, hay al menos una línea que pasa por A y B.
-
P2. Si A y B son puntos distintos, no hay más que una línea que pasa por A y B.
-
P3. Si A, B y C son puntos que no pasan por una misma línea, y D y E son puntos distintos tal que B, C, y D están en una línea y C, A, y E están sobre una línea, hay un punto F tal que A, B y F están en una línea y también D, E y F están en una línea.
-
Postulados de existencia:
-
P4. Existe al menos una línea.
-
P5. Sobre cualquier línea hay al menos tres puntos distintos.
-
P6. No todos los puntos están en la misma línea.
-
P7. No todos los puntos están en el mismo plano.
-
P8. Si S3 es un espacio tridimensional, todo punto está en S3.
Permítasenos ahora construir una representación para los postulados P1-P8. Representaremos un punto mediante una letra mayúscula A, B, C ; una línea por dos letras mayúsculas que representan puntos distintos sobre la línea AB, AC, BC o por una letra minúscula simple a, b, c ; y un plano por tres letras mayúsculas que representan tres puntos no-colineales del plano ABC, BCF o por una letra griega minúscula α, β... π...
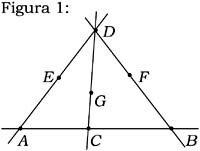
Existe una línea, digamos m, por el postulado P4, y por el postulado P5 esta línea contiene al menos tres puntos distintos, digamos A, B, C. También por el postulado P6 existe un punto D que no está sobre la línea m. Luego, por el P1 existen líneas DA, DB, DC y posiblemente otras que unen el punto D a los puntos de m. Más aun, por el postulado P5 cada una de esas líneas contiene otro punto, digamos E, F y G, como se muestra en la figura 1. En general, para cualquier AB y cualquier punto D que no está sobre AB, la totalidad de los puntos sobre las líneas que unen D a puntos de AB se llama el plano proyectivo ABD.
El postulado P7 indica que existe un punto H que no está sobre el plano ABD. Por el postulado P5 cada una de las líneas que unen H a puntos sobre ABD contienen al menos tres puntos distintos, como en la figura 2. En general, para cualquier plano proyectivo ABD y cualquier punto H que no es un punto sobre ABD, la totalidad de puntos sobre las líneas que unen H a puntos de ABD se llama el espacio proyectivo de tres dimensiones ABDH.
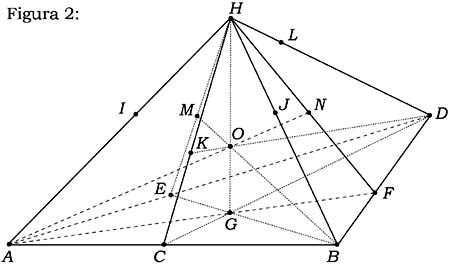
Como se expresó más arriba, aquí se procede desde unos pocos elementos primitivos y un puñado de reglas hasta construir el universo de las figuras geométricas que constituyen esta clase de geometría.
2. Geometría, unidad sintética y síntesis a priori
A lo largo de la historia de la filosofía, las matemáticas, y particularmente la geometría, han sido más que objetos de la curiosidad del filósofo. La lista más conocida de los que colocaron a esa rama de las matemáticas en el centro de sus reflexiones es aquella que va desde los pitagóricos, pasando por Platón, hasta Descartes y Spinoza. No obstante, esa lista puede ser ampliada significativamente incluyendo, en los siglos XVII y XVIII, claro está, a Leibniz, Hobbes y Kant, y en los siglos XIX y XX, a Helmholtz, Poincaré, Cassirer, Husserl y Carnap. Lo que tienen en común estos filósofos no es que simplemente se hayan ocupado de la geometría como objeto de estudio, sino que todos ellos consideraron que la geometría podía ser considerada como un verdadero modelo para todo conocimiento.
Ya ha sido mencionado cómo Descartes aplicó el método analítico de la geometría que él mismo desarrolló a las cuestiones de la teoría del conocimiento. Los casos de Leibniz, de Hobbes y de Kant son una expresión de la misma tendencia, pero con la diferencia de que vieron en los métodos de la geometría sintética un concepto que podían generalizar y trasladar a sus concepciones sobre la producción de todo el conocimiento humano, a saber, el concepto de construcción.
En Hobbes11 encontramos la afirmación de que las leyes del mecanismo que domina la naturaleza no son otra cosa que la expresión concreta de las leyes de la geometría. Por ello, sostiene que: Los que investigan la filosofía natural, si no toman de la geometría el principio de investigación, investigan en vano; y los que acerca de ella escriben o disertan, ignorantes de la geometría, abusan de sus lectores y de sus oyentes12. Y por el principio de la investigación geométrica no entiende otra cosa que el método constructivo, que llama método compositivo.
Spinoza, por su parte, además de su conocido esfuerzo por fundar la ética sobre bases geométricas13, intentó también una extensión de los principios de dicha disciplina, y en particular los de la geometría sintética, a la totalidad del conocimiento. En el Tractatus de intellectus emmendatione, en su doctrina de la definición14, sostiene que para que una definición sea perfecta, deberá expresar la esencia íntima de la cosa, es decir, no podrá incluir algo que no sea un atributo esencial de la misma. Y para que una definición tal sea posible, el intelecto procede forjándose causas internas en orden a su construcción. Dice Spinoza: Por ejemplo, para formar el concepto de la esfera decido figurarme una causa, a saber, un semicírculo que gira alrededor de su centro y que la esfera es como engendrada por la rotación15. Es decir, para Spinoza los conceptos no deben ser expuestos como conceptos acabados, como formas quietas, ya plasmadas, que nos limitamos a asimilar. La garantía incondicional de su verdad se obtiene únicamente en la medida en que hayamos penetrado en la ley de su devenir, de su génesis.
En el mismo contexto de la doctrina de la definición, Leibniz, quien, como los lógicos de Port Royal, distinguía entre definición nominal y definición real, sostiene que estas últimas son aquellas en las cuales debemos tener cuidado en establecer que la cosa es posible16, y esto solo puede hacerse procediendo a la construcción del objeto en cuestión. Dice Leibniz: El concepto de círculo propuesto por Euclides –a saber, que es la figura descrita por el movimiento de una línea recta en un plano alrededor de un punto fijo– proporciona una definición real, porque es claro que tal figura es posible17. Por lo que una definición real, desde su punto de vista, proporciona una regla mediante la cual construir un objeto desde una reunión de atributos y probar al mismo tiempo que este es posible. De acuerdo con Leibniz, este arte de construir, o, como él mismo lo llama, este arte de síntesis o combinación, es la ciencia que trata de las formas de las cosas, esto es, de la naturaleza cualitativa de los objetos, de lo semejante y de lo desemejante, y es justamente lo que hacen los geómetras cuando demuestran y ordenan proposiciones de acuerdo con su dependencia mutua18.
Ahora bien, el interés de Kant por las cuestiones geométricas se remonta a su juventud, a las obras que intentan resolver las disputas entre Newton y Leibniz sobre la naturaleza del espacio19, pero permanece en el centro de sus reflexiones durante toda su vida. En la Dissertatio (1770), no tiene dudas al afirmar que la geometría es prototipo de todo conocimiento sensible20, y que, como matemática pura, es el órgano de todo conocimiento intuitivo y distinto; y puesto que sus objetos no solo son los principios formales de toda intuición, sino que ellos mismos son intuiciones originarias, brinda un conocimiento en sumo grado verdadero, que es al mismo tiempo el modelo de la suma evidencia para los otros conocimientos21. ¿En qué radica, pues, que la geometría constituya un modelo para la evidencia de los otros conocimientos?
Permítaseme, para comenzar, considerar la conocida distinción kantiana entre juicios analíticos y sintéticos. De acuerdo con la elucidación que Kant provee de esta distinción en la introducción a la CRP, un juicio analítico es aquel que se obtiene mediante el análisis o descomposición de un concepto, colocando como predicado del juicio las notas obtenidas mediante dicho análisis. También llama a estos juicios explicativos, dado que lo único que hacen es desplegar o desarrollar22 el contenido del concepto del sujeto. Como afirmará más tarde (en la sección sobre El principio supremo de todos los juicios analíticos en A150-B190), el principio que rige la formación de los juicios analíticos es el principio de no-contradicción, pues este conduce a la afirmación del contenido del concepto del sujeto; es decir, dicho principio nos conmina a no colocar como predicado del juicio algo que contradiga el concepto del sujeto.
En cuanto a los juicios sintéticos, los cuales Kant también llama extensivos, la clave se encuentra precisamente en el hecho de que el predicado de dichos juicios agrega ciertas determinaciones al concepto del sujeto que no es posible encontrar en este mediante análisis conceptual. Aquí se da una composición genuina, una síntesis entre elementos heterogéneos. En la sección respectiva sobre El principio supremo de todos los juicios sintéticos (A154-B194), dice Kant: el principio supremo de todos los juicios sintéticos consiste en que todo objeto se halla sometido a las condiciones necesarias de la unidad que sintetiza en una experiencia posible lo diverso de la intuición23; es decir, que cualquier objeto que consideremos se constituye de acuerdo a una reunión sintética de caracteres que se dan en la intuición. Un objeto es, en este sentido, una construcción desde caracteres simples de acuerdo con una regla. ¿Dónde debemos buscar, de acuerdo con Kant, la clave de esta regla de unidad, y con ella la posibilidad de los juicios sintéticos? A esto responde: Es, pues, en el sentido interno, en la imaginación y en la apercepción donde hay que buscar la posibilidad de juicios sintéticos24.
De acuerdo con Kant, la conjunción de las representaciones, aquello que llamaremos propiamente un objeto, no puede venir ya dada a través de la sensibilidad, ni tampoco es obra de la forma pura de esta, esto es, ni espacio ni tiempo proveen de dicha conjunción, sino que obedece a un principio del entendimiento, es un acto de la espontaneidad de la facultad de representar25. Esta conjunción, que puede ser pura o empírica, sensible o intelectual, lleva, en la terminología kantiana, el nombre de síntesis (B130). Asimismo, al complejo constituido por la idea de una diversidad sometida a una función de reunión sintética lo llama Kant combinación. Pero esta combinación posee un elemento más que la distingue de una mera síntesis, y este es el concepto de unidad. Dice Kant: Combinar quiere decir representarse la unidad sintética de lo diverso26; es decir, combinar no es meramente sintetizar un conjunto de notas de una manera aleatoria, combinar es reunir sintéticamente cierta diversidad, pero acompañada de una unidad en la síntesis. En todos los juicios en los que se sintetizan ciertos elementos de acuerdo a conceptos existe una combinación en sentido estricto, pues la síntesis que allí opera es una síntesis acompañada de unidad.
Ahora bien, ¿en qué consiste dicha unidad? Consiste en que en cada acto de percepción reconozco a las representaciones que acuden a mi conciencia como mis representaciones, esto es, las refiero a una conciencia básica que las unifica y las conecta. Esta conciencia, el yo pienso, posibilita no solo la síntesis de la variedad de intuiciones que constituyen cada experiencia perceptiva, sino también la unidad de esas experiencias de modo tal que constituyen un conjunto unitario que reconozco como algo que me pertenece. Para ponerlo en otros términos, el yo pienso es un principio formal27 sintético originario responsable no solo de la constitución de nuestras experiencias perceptivas individuales, sino de la conjunción de las mismas en una totalidad ordenada, estable y consistente; es decir, es el principio responsable de la objetividad de nuestra visión del mundo. Como dice Kant: Como dada a priori, la unidad sintética de lo diverso de las intuiciones constituye, pues, el fundamento de la identidad de la misma apercepción que precede a priori a todo mi pensamiento determinado28.
Es esta facultad fundamental de enlace de las representaciones la que posibilita la construcción de juicios sintéticos y por ende la construcción de conocimientos. Conocer es, desde el punto de vista de Kant, construir un objeto mediante la reunión sintética de caracteres e introducirlo dentro de una totalidad consistente. Y no es casual que Kant ejemplifique este punto con un caso extraído de la geometría: Para conocer algo en el espacio, una línea, por ejemplo, hay que trazarla y, por consiguiente, efectuar sintéticamente una determinada combinación de la variedad dada, de forma que la unidad de este acto es, a la vez, la unidad de conciencia (en el concepto de línea), y es a través de ella como se conoce un objeto (un espacio determinado)29. Aquí se expone con claridad el procedimiento constructivo que señalamos como característico de la geometría sintética. Podría decirse que la variedad dada a la que se refiere Kant son los puntos, y la determinada combinación, los dos primeros axiomas de Euclides. Lo que interesa es que a continuación de este pasaje agregue Kant con énfasis: La unidad sintética de la conciencia es, pues, una condición objetiva de todo conocimiento30. En mi opinión, Kant eleva el método sintético de la geometría a principio universal de construcción del conocimiento.
Pero analicemos el otro componente importante que Kant menciona como clave de la construcción de juicios sintéticos, a saber, la imaginación. En la sección titulada La aplicación de las categorías a los objetos de los sentidos en general de la segunda edición, Kant distingue entre síntesis intelectual y síntesis figurativa. La primera es la que se refiere a la unidad de los objetos de la intuición en general, en relación a la unidad de apercepción. La segunda se refiere a la aplicación de la misma unidad de apercepción, y con ello de las categorías, pero concretamente a la diversidad de la intuición sensible a priori. Esta síntesis es, en sus palabras: la condición a la que necesariamente han de someterse todos los objetos de nuestra intuición31. Kant llama a esta síntesis síntesis trascendental de la imaginación.
Uno se pregunta de inmediato qué tiene que ver la imaginación en este punto, y Kant argumenta de una manera bastante oscura como para extraer una idea clara al respecto. Tal vez podríamos primero intentar hacernos una idea del proceso de síntesis que Kant está concibiendo y luego ver por qué la imaginación tiene un papel importante en él. Para ello, consideremos el ejemplo que Kant mismo propone en B154, donde dice: Esto lo percibimos siempre en nosotros. No podemos pensar una línea sin trazarla en el pensamiento, ni un círculo sin describirlo, como tampoco representar tres dimensiones del espacio sin construir tres líneas perpendiculares a partir del mismo punto. Desde mi punto de vista, no es casual que el ejemplo sea extraído de la geometría, como tampoco es casual que en él aparezca el verbo construir y otros dos términos en cursivas que entrañan la idea de construcción. Por ello, dirigiré mi atención hacia la forma en que Kant concibe la producción del conocimiento geométrico y veré si allí pueden encontrarse las claves de la síntesis figurativa.
En las Observaciones generales sobre la estética trascendental, Kant se pregunta acerca de las proposiciones de la geometría: ¿de dónde sacamos semejantes proposiciones y en qué se apoya nuestro entendimiento para llegar a tales verdades absolutamente necesarias y universalmente válidas?32. Y la respuesta es que un conocimiento de ese tipo solo podría obtenerse de dos fuentes, a saber, intuiciones o conceptos. Dado que ambos están dados a priori o a posteriori, debemos considerar cada una de estas opciones. Es claro que, si como Kant parece creer (y nadie en el siglo XVIII creería lo contrario33), la geometría es una disciplina constituida por verdades universales y necesarias, no podría derivar sus proposiciones de conceptos empíricos y de sus intuiciones correspondientes, pues dicha cosa convertiría a la geometría en una disciplina irremediablemente empírica. Solo quedan las opciones de que el conocimiento geométrico se derive o bien de conceptos puros, o bien de intuiciones a priori. Lo primero es desechado apelando a la definición de analiticidad y a la imposibilidad de explicar un juicio de la geometría en base a dicha idea. Entonces, la única opción que queda es considerar que las proposiciones de la geometría se derivan de intuiciones puras. Pero aquí Kant plantea una distinción, dice: Pero, ¿de qué clase de intuición pura se trata: a priori o empírica?34. En mi opinión, una intuición pura empírica sería una representación inmediata de un momento particular del tiempo o un espacio particular no actual, por ejemplo, la representación que puedo tener en este momento en que escribo este trabajo del aula de la universidad donde imparto un curso sobre la Crítica de la razón pura. Se trata de una representación independiente de la experiencia del caso, pero no independiente de toda experiencia. Y esto es posible por la intervención de la facultad de imaginación, aunque de una imaginación puramente reproductiva. Asimismo, se trataría de una representación que no es universalmente válida, sino de una que tiene una validez puramente subjetiva.
Por otro lado, una intuición pura a priori sería una representación que surge como una necesidad de la forma pura de la sensibilidad, independiente de los caracteres sensibles pasados o actuales, pero no completamente independiente de toda clase de representación sensible. No olvidemos que, para Kant, la geometría, y en general todo el conocimiento matemático, es conocimiento por construcción de conceptos, esto es, un conocimiento en el cual es imprescindible presentar la intuición a priori correspondiente al concepto. Se trata, según Kant, de una representación que, en tanto intuición, es una representación de un objeto singular. Sin embargo, en la medida en que se construye allí un concepto, dicha representación tiene que expresar las propiedades comunes a dicha clase de representaciones; es decir, debe tener validez universal. En A714-B742 dice: Construyo, por ejemplo, un triángulo representando, sea el objeto correspondiente a este concepto por medio de la simple imaginación, en la intuición pura, sea, de acuerdo con esta, sobre el papel, en la intuición empírica, pero en ambos casos completamente a priori, sin tomar el modelo de la experiencia. La imaginación, encargada de la construcción misma, procede no de una manera meramente reproductiva, sino esencialmente productiva, pues, como el propio Kant afirma, no toma el modelo de la experiencia; es decir, hace abstracción de las circunstancias específicamente sensibles que constituyen una figura geométrica concreta (por ejemplo, la magnitud de sus lados y ángulos), destacando las propiedades universales que la representación particular está instanciando. Para ponerlo en términos que serán más claros con posterioridad, las figuras geométricas construidas en la intuición pura constituyen representaciones de las propiedades invariantes que caracterizan a dicha clase de figuras.
Volvamos ahora a la síntesis figurativa. Tal vez ahora tenga más sentido la definición que Kant da de la imaginación como la facultad de representar un objeto en la intuición incluso cuando este no se halla presente35. En la síntesis figurativa, la imaginación es la única que puede suministrar a priori la variedad sensible en orden a que el entendimiento, a través de la unidad sintética de la apercepción, lleve a cabo la síntesis de la misma regida por las categorías. No obstante, según Kant, es la imaginación misma la que produce la síntesis, aunque regida por las categorías, y esto se justifica porque aquí estamos tratando de la aplicación de las categorías a la sensibilidad, no de la síntesis meramente pensada en la categoría (síntesis intelectual). Y nuevamente el caso de la geometría nos ilustra el punto: En esta síntesis sucesiva de la imaginación productiva se basan, para producir las figuras, las matemáticas de la extensión (geometría) con sus axiomas36.
Así, parece que la síntesis figurativa procede, en relación a todo el conocimiento sintético, bajo el modelo de construcción de conceptos que se lleva a cabo en las matemáticas y en especial en la geometría pura. La imaginación productiva, aquella que no sigue el modelo de la experiencia, no solo es capaz de presentar a priori las intuiciones correspondientes, sino que construye los objetos del conocimiento de acuerdo a una regla dictada por el entendimiento. De este modo, la idea de construcción, principio fundamental de la geometría sintética, se constituye como el principio fundamental de todo conocimiento sintético. Y esta es la razón por la que he estado hablando de juicios sintéticos sin distinguir, como lo hace Kant, entre juicios sintéticos a priori y juicios sintéticos a posteriori. Pues el principio que los hace posibles es exactamente el mismo, siendo la diferencia que, en el primer caso, las construcciones ocurren a priori y, en el segundo, a posteriori. Kant deja claro este punto en la sección 6 de los Prolegómenos, donde dice: Esta observación con respecto a la naturaleza de la matemática, nos conduce a la primera y superior condición de su posibilidad, a saber: debe haber en su fondo alguna intuición en la cual pueda presentar todos sus conceptos in concreto, y, sin embargo, a priori, o, como se dice, construirlos pues así como la intuición empírica hace posible, sin dificultad, que el concepto que nos formamos de un objeto de la intuición se amplíe sintéticamente en la experiencia por nuevos predicados que ofrece la intuición misma, así puede hacerlo también la intuición pura, solamente con esta diferencia: que, en el último caso, los juicios sintéticos habrán de ser a priori, ciertos y apodícticos; pero, en el primero, solamente a posteriori y empíricamente ciertos37.
Quisiera, para terminar esta sección, destacar un punto que no hice explícito en la exposición anterior, pero que resultará de crucial importancia para el problema que enfrento: desde el punto de vista de Kant, cabe distinguir entre el principio activo de constitución de la experiencia, esto es, la originaria unidad sintética de apercepción a través de la síntesis figurativa, y las reglas que dictan los criterios de unidad que dicha función sigue, la estructura de las intuiciones puras y las categorías. La relevancia de esta distinción quedará de manifiesto en lo que sigue.
3. La teoría de grupos y lo a priori constitutivo
En la sección anterior examinamos la concepción de Kant según la cual la función constitutiva del conocimiento descansa en un principio básico de unificación que tiene fuertes símiles con el método de la geometría sintética que describimos en la sección 1. Al igual que en el ejemplo allí considerado de la construcción del plano y el espacio proyectivo desde los elementos primitivos, y de acuerdo con los axiomas de incidencia y existencia, la constitución que lleva a cabo, según Kant, el entendimiento parte de la variedad a priori de la sensibilidad y, de acuerdo con reglas a priori, construye todo juicio sintético. Así, para Kant, la constitución de la experiencia procede a través de la combinación de regla y principio activo, axioma o concepto y unidad sintética de apercepción38. De acuerdo con las especificaciones que Kant dio a estos axiomas y conceptos y del alcance de su determinación sobre la función constitutiva, el resultado de dicha combinación es la construcción de un mundo de estructura euclideana y newtoniana39.
Sin embargo, desde el siglo XIX ocurrieron, tanto en las ciencias formales como en las fácticas, cambios de una magnitud tal que llevaron a cuestionar el modelo de explicación del conocimiento propuesto por Kant. Primero con el surgimiento de las geometrías no-euclideanas, lo cual hizo tambalear la noción kantiana de intuición, y luego con el surgimiento de la teoría de la relatividad, la cual definía un marco espacio-temporal radicalmente nuevo, afectando el contenido de la tabla de las categorías, poco parecía que podía rescatarse de la epistemología kantiana. No obstante, varios autores, tanto en el siglo XIX como a comienzos del XX, intentaron salvar parte del espíritu kantiano a la vez que reconocían los cambios profundos que las revoluciones en la ciencia traían consigo.
El desafío consistió en separar la función estrictamente constitutiva, el principio activo de la síntesis, de las reglas que condicionan los tipos de síntesis a efectuarse. Es decir, el reto consistía (y consiste) en retener como función constitutiva básica algo que no tuviera la forma de un principio o enunciado particular, porque cualesquiera de esos podrían ser transformados, o reemplazados, o rechazados.
En el siglo XIX, algunos filósofos relacionados a las matemáticas, como el caso de Helmholtz y Poincaré40, comenzaron a explotar las virtudes de un concepto fundamental: el concepto de grupo de transformaciones. Más tarde, y habiéndose ya trasladado ese concepto al seno de la geometría por parte de Klein, en lo que se llamó el programa de Erlanger o la teoría de los invariantes geométricos, otros filósofos como Cassirer y Husserl41 vieron allí una herramienta poderosa para capturar lo que se buscaba, a saber, una función de síntesis clara y separada de cualesquiera especificaciones.
Esas concepciones no fueron lo suficientemente valoradas en su momento, pero en mi opinión encerraban elementos que podríamos utilizar hoy en día para articular una noción amplia de a priori constitutivo42. El principio fundamental de esta posición es que en la cognición en general llevamos a cabo una búsqueda y constitución de invariantes; donde por búsqueda y constitución se entiende la aplicación, sobre una variedad dada, de un principio de síntesis fundamental que podemos identificar con el concepto matemático de grupo de transformaciones, el cual obedece ciertas reglas que determinan ciertos órdenes de invariantes, esto es, la forma de la experiencia. Tanto el principio responsable de la síntesis, como los conceptos fundamentales que dictan la regla de constitución son a priori, atributos de aquello que llamamos racionalidad.
Dado que excedería los límites y las pretensiones de este trabajo proveer de una teoría de la experiencia que haga uso de los conceptos de grupo de transformaciones y de invariantes, procederé en primer lugar a exponer el concepto de grupo de transformaciones para luego mostrar cómo en, por lo menos, tres áreas importantes de la cognición la aplicación de dicho concepto y la constitución de invariantes es fundamental, a saber, las matemáticas, la física y la percepción43.
Los conceptos de transformación y grupo de transformaciones se deben a dos prominentes matemáticos ingleses, Arthur Cayley (1821-1895) y James Sylvester (1814-1897). Pero antes de dar una definición precisa de transformación, es necesario explicar la idea de mapeo44.
Definición: Un mapeo de un conjunto A en un conjunto B es un emparejamiento de elementos de A y un subconjunto de B de modo que cada elemento de A es emparejado con exactamente un elemento del subconjunto de B, y cada elemento de tal subconjunto de B es emparejado con al menos un elemento de A. El caso especial de un mapeo de un conjunto A en un conjunto B para el cual cada elemento de B es emparejado con al menos un elemento de A se llama un mapeo del conjunto A sobre el conjunto B.
Definición: F es un mapeo de un conjunto A en un conjunto B si para todo elemento a de A existe un único elemento b de B que se empareja con a; este emparejamiento se denota por f(a) = b. El conjunto A se llama el dominio de f, y el conjunto B el codominio de f.
Definición: Un mapeo f de A a B es uno a uno si cada elemento en el rango de f es la imagen de exactamente un elemento de A. Esto es, si f(a) = f(c), entonces a = c.
Definición de transformación: Una transformación es un mapeo de A sobre B tal que cada elemento de B es la imagen de exactamente un elemento de A. Es decir, una transformación es un mapeo que es uno a uno y sobre. Definición de grupo de transformaciones: Un grupo de transformaciones de un conjunto A sobre sí mismo es un conjunto S no vacío junto con una operación tal que:
-
Si f y g están en S, entonces fg y gf están en S. (Cerradura)
-
Si f, g y h están en S, luego (fg)h = f(gh). (Asociatividad)
-
Hay un único elemento en S que satisface If = f I = f para todo f en S. (Identidad)
-
Dado f en S, existe un único elemento f -1 que satisface f -1 f = f f -1 = I. (Inverso)
La propiedad de cerradura significa que el producto de cualesquiera dos transformaciones en el conjunto es también una transformación en el conjunto.
La segunda de las propiedades es la de asociatividad. La notación de f(gh) y (fg)h indica el producto de las mismas tres transformaciones en el mismo orden. Por ejemplo, considérese las siguientes tres transformaciones que han sido definidas como sigue:
-
f : x ! x + 3
-
g : x ! x – 2
-
h : x ! 2x
-
f(gh) : x ! ([2x] – 2) + 3 = 2x + 1
-
(fg)h : x ! 2x + (– 2 + 3) = 2x + 1
La tercera propiedad establece la existencia de una única identidad. Dado que el producto de una transformación y la identidad es la transformación, el efecto de la identidad es dejar a cada punto invariante.
La cuarta propiedad establece la existencia de una única transformación inversa para cada transformación del conjunto. Dado que el producto de una transformación y su inversa es la identidad, el efecto de la inversa es deshacer la transformación, retornando cada punto a la posición original.
Al igual que ya lo había sido el número, el concepto de grupo es visto como un principio fundamental de orden, con la diferencia de que lo que se trae a una unidad no son elementos sino operaciones. La creación de la serie de los números naturales empezó con haberse fijado un primer elemento y con haberse dado una regla que permite generar siempre nuevos elementos mediante su repetida aplicación. Todos los elementos fueron unidos en una totalidad unitaria en virtud de que cada conexión efectuada entre elementos de la serie de los números define un nuevo número. Si formamos la suma de dos números a y b o bien su diferencia, su producto, etc., los valores a + b, a – b, a . b no salen de la serie básica sino que pertenecen a ella misma ocupando una posición determinada en ella, o bien pueden ser referidos indirectamente a los elementos de la serie básica de acuerdo con reglas fijas. Así pues, por más que avancemos a través de nuevas síntesis, tenemos la seguridad de que el marco lógico de nuestra investigación no será nunca completamente roto, por más que se tenga que ampliar. La idea del reino unitario de los números significa justamente que la combinación de operaciones aritméticas, por numerosas que sean, conducen siempre finalmente a elementos aritméticos. En la teoría de grupos se eleva el mismo punto de vista a un grado de estricta y verdadera universalidad, ya que en dicha teoría se ha eliminado, por así decirlo, el dualismo de elementos y operación; la operación misma se ha convertido en elemento. Así como Kepler llamó al número el objeto del espíritu que nos permite ver la realidad, podemos decir también válidamente de la teoría de grupos, la cual ha sido llamada el ejemplo más brillante de matemática puramente intelectual45, que ella ha hecho posible la interpretación de ciertas conexiones espaciales, físicas y perceptivas. Consideremos ahora estas diferentes aplicaciones.
Cuando es aplicado a la geometría, un grupo se forma por todas las transformaciones geométricas que resultan cuando permitimos que los elementos se muevan en el espacio tridimensional ordinario. En este concepto de grupo, se obtiene un principio general de clasificación mediante el cual los diferentes tipos de geometrías pueden ser unificados bajo un punto de vista simple. Si planteamos la pregunta acerca de qué debemos considerar como una geometría, la respuesta es: aquellas propiedades que permanecen invariantes a través de ciertas transformaciones espaciales; es decir, aquellas estructuras que persisten cuando variamos la posición absoluta de esta estructura en el espacio, cuando aumentamos o disminuimos proporcionalmente la magnitud absoluta de sus partes, o cuando finalmente revertimos la ordenación de las partes individuales, como cuando sustituimos la figura original por otra que se relaciona con ella como con su imagen en un espejo.
Felix Klein convirtió esta idea en el centro del llamado Erlanger Programm; podemos apreciarla en el siguiente pasaje: Dado cualquier grupo de transformaciones en el espacio que incluye el grupo principal como un subgrupo, la teoría invariante de este grupo proporciona un tipo definido de geometría, y toda posible geometría puede ser obtenida en esta forma46. El sentido de este pasaje puede ser explicado de la siguiente manera: las diferencias entre las geometrías son de hecho las diferencias entre las relaciones que ellas exploran. Las relaciones o propiedades que una geometría explora son aquellas que son invariantes bajo un conjunto o grupo de transformaciones; las propiedades invariantes y las transformaciones permitidas se determinan mutuamente una a otra, de modo que la geometría puede ser caracterizada por las propiedades invariantes o el grupo de transformaciones.
Los grupos de transformaciones a los cuales se someten las figuras geométricas varían en su grado de radicalidad, y, en la medida en que esta radicalidad es mayor, las propiedades invariantes son también más generales. Esto posibilita clasificar las geometrías en relación con este grado de generalidad producido por el grado de radicalidad en las transformaciones, cada una conteniendo a la anterior. En la cima de la clasificación encontramos a la topología, a esta le sigue la geometría proyectiva, y a esta, la geometría euclideana.
La geometría euclideana es el estudio de las propiedades invariantes bajo el grupo de los así llamados movimientos rígidos, a saber, traslación, rotación y reflexión. La propiedad esencial preservada por este grupo de movimientos es la distancia, es decir, la característica de la isometría.
La geometría proyectiva es el estudio de las propiedades de conjuntos de puntos que son invariantes bajo el grupo de transformaciones proyectivas. Estas transformaciones, que posibilitan las así llamadas figuras de perspectiva, constituyen un mapeo uno a uno sobre puntos, es decir, existe una correspondencia uno a uno de elementos correspondientes y una relación de incidencia compartida por dichos elementos. Las relaciones que se preservan bajo estas condiciones son las de incidencia y existencia, es decir, la copuntualidad de los puntos, la colinealidad de las líneas y la coplanalidad de los planos. De este modo, las relaciones que explora la geometría proyectiva son relaciones de incidencia, con independencia completa de las relaciones de magnitud.
Por último, la topología es el estudio de las propiedades de un conjunto de puntos invariantes bajo el grupo de transformaciones bicontinuas del espacio sobre sí mismo. Una transformación f es bicontinua, o se llama un homeomorfismo, si y solo si f y f-1 son ambas continuas. Una transformación de puntos en la región plana S1 sobre puntos en la región plana S2 es continua si para todo punto de S2 y cada número positivo å hay un número positivo ä tal que la imagen de cualquier punto de S1 que está en la vecindad de un punto A con radio ä está en la vecindad de la imagen de A con radio å. La propiedad invariante fundamental que arroja el conjunto de transformaciones topológicas es la de conectividad de un conjunto de puntos. Un conjunto está conectado si y solo si cualesquiera dos puntos del conjunto pueden ser unidos por alguna curva que está completamente en el conjunto.
Pasemos ahora al caso de la percepción. De acuerdo con una tesis sostenida ya por psicólogos de la talla de Katz, Buehler, Brunswik y Frischeisen-Koehler, y defendida en nuestros días por investigadores como Roger Shepard, entre otros, la percepción no se encuentra confinada a un aquí y ahora, sino que expande el dato particular y lo integra en una experiencia total, y es solo en virtud de esta integración que la percepción puede ejercitar su función propia como un factor objetivo en el conocimiento. Si la percepción estuviera limitada al flujo de las impresiones, se desintegraría, pues cada una de esas impresiones presenta la medida, la forma y el color de los objetos de una manera diferente.
Como una cuestión de hecho, sostienen los psicólogos, la percepción no se atiene a esta sucesión caleidoscópica de imágenes, sino que construye desde ellas la verdadera forma perceptual. Por ejemplo, dependiendo de las circunstancias en las que un objeto es visto, la iluminación solar se encuentra sujeta a una gran variación en composición espectral. La luz que golpea un objeto directamente desde el sol puede ser más fuerte en mediana longitud de onda (amarillos), la luz esparcida sobre un objeto desde un cielo claro puede ser más fuerte en longitud de ondas bajas (azules), y la luz desde un entorno solar puede ser más fuerte en longitudes de onda altas (rojos). Dependiendo de tales condiciones de la visión, la luz esparcida a nuestros ojos desde cualquier objeto dado puede estar fuertemente dirigida hacia longitudes de onda bajas, medias o altas, y así hacia amarillos, azules o rojos. Sin embargo, a pesar de esas grandes variaciones en la luz que una superficie esparce sobre nuestros ojos bajo esas diferentes condiciones, el color que percibimos en una superficie permanece como una propiedad fija y aparentemente inherente en la cosa misma47.
Así, desde el punto de vista de la evidencia suministrada por la psicología de la percepción, podemos decir con propiedad que esta se encuentra dominada por un factor constitutivo que se manifiesta en la posibilidad de formar invariantes. La inestabilidad original del flujo de nuestras impresiones es, en virtud de esta función de constitución de invariantes, sustituida por un mundo de objetos estables, permanentes, rasgos esenciales de lo que propiamente llamamos un mundo objetivo. La percepción es posible a través de un proceso que podemos propiamente llamar idealizatorio, en la medida en que se introduce en el flujo de las impresiones sensoriales una estructura que de manera alguna se encontraba determinada de antemano.
La ciencia física, por su parte, parece operar de una manera análoga: introduce, aunque en mi opinión ya no sobre el flujo de las impresiones, sino sobre el mundo de la percepción ordinaria, estructuras y determinaciones más refinadas que alcanzan cierta perfección en la forma. Quizás en la práctica científica idealizatoria encontremos la perfección en la búsqueda y constitución de invariantes, algo que no podemos sostener que sea el caso en la experiencia ordinaria, pues, como también ha enseñado la psicología empírica, hay límites a la constancia perceptual. En la física, por el contrario, una vez que el grupo de transformaciones se especifica, todas las modificaciones que son posibles con respecto a este grupo pueden ser determinadas por medio de leyes exactas.
Conocida es la importancia que la física ha concedido a las transformaciones de Lorentz48, que determinan que algo sea considerado más objetivo que otra cosa si es invariante bajo dichas transformaciones. Einstein nos enseñó que la medida temporal y espacial son relativas a un observador; sus magnitudes serán medidas diferentemente por diferentes observadores inerciales, y los intervalos espaciales y temporales no son invariantes bajo las transformaciones de Lorentz. No obstante, los observadores inerciales coincidirán acerca de otro intervalo entre sucesos que envuelve no solo separaciones temporales o espaciales, sino una mezcla de ambos, a saber, la raíz cuadrada del cuadrado de la separación temporal menos el cuadrado de la separación espacial. Este intervalo más complicado es invariante bajo las transformaciones de Lorentz. El principio de la relatividad de la teoría especial de la relatividad de Einstein sostiene que todas las leyes de la física son las mismas para todos los observadores inerciales; son las mismas en todo marco de referencia inercial y por ende son invariantes bajo las transformaciones de Lorentz. No es de extrañar, pues, que Einstein dijera que antes de llamar a su teoría teoría de la relatividad, la había llamado teoría de los invariantes49.
Conclusiones
Permítaseme, para concluir, volver un momento a Kant. En la Analítica de los principios, en el capítulo sobre El esquematismo de los conceptos puros del entendimiento, Kant enfrenta el problema de mostrar qué es lo que posibilita que los objetos sean subsumidos bajo conceptos; en otras palabras, se preocupa por elucidar la manera en la cual el ámbito conceptual a priori determina lo dado en la experiencia. De acuerdo con Kant, cuando decimos que un objeto está contenido en un concepto, lo que queremos decir es que el concepto debe incluir lo representado en el objeto que haya de subsumir. Ahora bien, los conceptos puros del entendimiento, que contienen las reglas a priori de la determinación de los fenómenos y por ello son libres de toda experiencia, necesitan un término que les provea del contenido empírico al cual van dirigidos. Este contenido, en su caso, no puede ser más que una condición formal de la sensibilidad que suministre la regla de síntesis de los fenómenos. Esta condición formal y pura de la sensibilidad es lo que Kant llama esquema de los conceptos.
Un esquema, de acuerdo con Kant, debe ser distinguido netamente de una imagen. Esta es un producto de la imaginación reproductiva, y, como tal, es siempre particular. En cambio, el caso del esquema, dado que tiene que posibilitar la aplicación de un universal, no puede ser una representación meramente particular, sino algo que al mismo tiempo sea intelectual y sensible. Si pensamos que un concepto, según Kant, es una regla a priori de síntesis de las representaciones, y que el esquema, siendo un producto de la imaginación, es por ende el producto de una facultad sensible, parece que lo que Kant estaría sugiriendo es que dicho esquema es una especie de imagen determinada por un concepto, lo cual la hace diferente de una mera imagen. Así parece pensar cuando dice: Así, si escribo cinco puntos seguidos..., tengo una imagen del número cinco. Si, por el contrario, pienso simplemente un número en general, sea el cinco, sea el cien, tal pensar es un método para representar, de acuerdo con cierto concepto, una cantidad en una imagen, más que esa imagen misma, que, en este último caso difícilmente podría yo abarcar y comparar con el concepto50. Lo que quiero sugerir es que por esquema Kant está entendiendo la imagen de aquellas propiedades comunes a varios objetos particulares, la cual es un producto de la imaginación productiva a priori regida por un concepto. De este modo, el esquema representa las propiedades invariantes o esenciales de un objeto, y surge de la determinación de las imágenes particulares de acuerdo a una regla a priori que es el concepto. En su opinión, esta función no está reservada a los conceptos puros, sino que incluye también a los conceptos empíricos. Dice Kant: El concepto de perro significa una regla conforme a la cual mi imaginación es capaz de dibujar la figura de un animal cuadrúpedo en general, sin estar limitada ni a una figura particular que me ofrezca la experiencia ni a cualquier posible imagen que pueda representar en concreto51. Entonces, parece que para Kant la aplicación de un concepto, y con ello la posibilidad del objeto mismo, depende de la búsqueda y constitución de invariantes en el flujo de la experiencia, lo cual procede mediante el recurso a los esquemas trascendentales.
En nuestra sección anterior hemos mostrado cómo las matemáticas, la física y la percepción misma exhiben, aunque con diferentes grados de precisión, una estabilidad y permanencia en sus respectivas estructuras. En mi opinión, esta invariancia, que constituye los rasgos más generales de aquello que llamamos el mundo objetivo, es resultado de la aplicación de un principio sintético formal y originario que se asienta en el entendimiento humano y que, conjuntamente con los principios que determinan el orden mismo de lo invariante, nos caracteriza como sujetos racionales. Los objetos matemáticos, así como los acontecimientos físicos y nuestros objetos de percepción ordinaria, son el resultado de una operación que, recorriendo una variedad de elementos simples, los unifica formando clases de objetos que comparten un mismo conjunto de propiedades estructurales y permanentes. El concepto de grupo de transformaciones puede verse como ese principio sintético fundamental responsable de las síntesis que se llevan a cabo en los diferentes dominios de la cognición. Queda, no obstante, el trabajo no menor de teorizar no solo sobre la naturaleza de esta función constitutivo-formal, sino también sobre las especificaciones o, por decirlo en la propia jerga de la teoría de grupos, sobre las transformaciones permisibles que determinan el conjunto de propiedades invariantes que atraviesan los diferentes dominios de la cognición. Es decir, quedan por especificar cuáles serían aquellas categorías más generales cuya regla obedece el principio formal de la síntesis. Y, en este asunto, tal vez podríamos identificar dos conjuntos de condiciones: uno a priori, universal y necesario, ahistórico y asentado en la estructura de nuestra racionalidad; y otro convencional e histórico. Pero el desarrollo de este punto es tema de otro trabajo.
-
1 En la nota al pie correspondiente a B134, Kant afirma, en una frase bien conocida, que: La unidad sintética de apercepción es, por tanto, el concepto más elevado del que ha de depender todo uso del entendimiento, incluida la lógica entera y, en conformidad con ella, la filosofía trascendental. Es más, esa facultad es el entendimiento mismo (Kant, I., Crítica de la razón pura, Madrid: Alfaguara, 1988; en adelante: CRP).
-
2 Euclides, Elementos de geometría, Madrid: Gredos, 2000, p. 43.
-
3 Ibid.
-
4 Ibid.
-
5 Ibid., p. 44.
-
6 Ibid., pp. 19-23.
-
7 Descartes, R., Reglas para la dirección del espíritu, México D.F.: Porrúa, 2001, p. 163.
-
8 Puede encontrarse una historia detallada de estos desarrollos en el capítulo II de mi disertación doctoral, De lo sintético a priori a lo a priori formal constitutivo. La geometría y la evolución de lo a priori de Kant a Carnap, México D.F.: UNAM, 2005 (inédito).
-
9 Es claro que dichos postulados pueden ser extendidos de tal manera que en función de ellos pueda definirse igualmente un n-espacio.
-
10 El término incidencia en esta frase se usa para indicar la propiedad de que una línea está sobre un punto o que un punto está sobre una línea.
-
11 Véase especialmente: Hobbes, T., Hobbes: Antología, Barcelona: Península, 1987.
-
12 Ibid., p. 112.
-
13 Su Ética demostrada según el orden geométrico fue erigida sobre el modelo de los Elementos de Euclides.
-
14 En las secciones 51ss.
-
15 Spinoza, B., Tratado de la reforma del entendimiento, Madrid: Tecnos, 1989, p. 36.
-
16 Leibniz, G.W., Of Universal Synthesis and Analysis; or, of the Art of Discovery and of Judgment, en: Parkinson, G.H.R. (ed.), Leibniz. Philosophical Writings, Londres: Rowman and Littlefield, 1983, p. 12.
-
17 Ibid.
-
18 Ibid., p. 10.
-
19 Entre estas obras podemos mencionar: Pensamientos sobre la verdadera estimación de las fuerzas vivas (1746), Nueva elucidación de los primeros principios de la cognición metafísica (1755), Historia natural universal y teoría de los cielos (1755), Monadología física (1756).
-
20 Kant, I., Principios formales del mundo sensible y del inteligible, Madrid: CSIC, 1996, p. 13.
-
21 Ibid., p. 16.
-
22 La raíz latina del término explicar puede ayudar a entender la idea subyacente. El verbo explico, explicare es un compuesto del verbo básico plico, plicare y de la preposición ex. Plico significa doblar, plegar; esto, unido a la preposición ex, significaría doblar hacia fuera o desplegar, también desarrollar.
-
23 CRP, A158-B197.
-
24 Ibid., A155-B194. No deseo entrar en una discusión aquí, pero debo apuntar mi discrepancia con J.A. Coffa, quien al comienzo de su ya famoso The Semantic Tradition from Kant to Carnap: To the Viena Station, Cambridge: Cambridge University Press, 1991, interpreta a Kant como sosteniendo que la base de los juicios sintéticos es la intuición. Es sobre este énfasis que Coffa sostiene su historia de la tradición semántica, la cual, en su opinión, recoge los resultados de la crisis a la que la revolución en geometría del siglo XIX condujo a la intuición, y con ello a la idea de lo a priori constitutivo. En mi disertación doctoral, ya citada en la nota 8, discuto pormenorizadamente este asunto con la interpretación de Coffa.
-
25 CRP, B130.
-
26 Ibid., B131.
-
27 Al referirme al yo pienso como principio formal, me hago eco de la propia distinción kantiana entre apercepción pura u originaria y empírica, dado que Kant define a la primera como aquella que debe poder acompañar a toda representación, pero que no puede estar acompañada por ninguna otra representación. Asimismo, es de fundamental importancia en este sentido la afirmación de Kant respecto de que dado que nuestro entendimiento no es productor de su propio contenido, se sigue su naturaleza típicamente sintetizadora (cf. ibid., B136).
-
28 Ibid., B134.
-
29 Ibid., B138.
-
30 Ibid.
-
31 Ibid., B151.
-
32 Ibid., B64-A47.
-
33 En el siglo XIX, en cambio, el surgimiento de las geometrías no-euclideanas hizo pensar a algunos que la geometría podría ser empírica. Gauss trató de determinar directamente, por medio de la triangulación ordinaria realizada con instrumentos topográficos, si la suma de los ángulos de un gran triángulo es igual a la suma de dos ángulos rectos o no. Ejecutó sus mediciones sobre un triángulo formado por tres montañas, la de Brocken, la de Hoger y Hagen, y la de Inselberg, cuyos lados miden 69, 85 y 107 kilómetros. Es innecesario decir que no detectó ninguna desviación de 180º dentro del margen de error, lo que debe haber desilusionado a Gauss.
-
34 CRP, A48-B65.
-
35 Ibid., B151.
-
36 Ibid., B204.
-
37 Kant, I., Prolegómenos a toda metafísica del provenir, México D.F.: Porrúa, 1991, p. 41.
-
38 En CRP, A116, Kant deja en claro que lo que allí llama apercepción pura debe presuponerse antes de hablar siquiera de intuiciones, pues estas solo tienen sentido en virtud de la necesaria conexión de unas con otras en una única conciencia.
-
39 Es claro que no podemos culpar a Kant por no haber presenciado más que lo que la ciencia de su época le mostraba. Esto lo condujo a tratar de probar la unicidad de nuestro esquema conceptual. Parte del esfuerzo de la Analítica consiste en mostrar que el mundo, tal como lo experimentamos, es posible por la conjunción de un único y determinado conjunto de condiciones subjetivas.
-
40 Para una exposición de la forma en que Poincaré hizo uso de este concepto véase mi Idealización, constitución y convención en la filosofía de la geometría de Henri Poincaré, en: Txapartegi, E. (comp.), Los objetos de la ciencia. El mundo que la ciencia construye, Córdoba: Brujas, 2005.
-
41 Para una elucidación de las concepciones de estos filósofos, aunque en relación a la influencia que ejercieron en el pensamiento temprano de Carnap, remito a mi artículo La teoría de grupos y el espacio intuitivo en Der Raum de Rudolf Carnap, de próxima publicación en Diánoia.
-
42 En años recientes han proliferado diversas e interesantes concepciones de lo a priori apoyadas en Kant o en concepciones racionalistas más tradicionales. Sin embargo, la mayoría de ellas o bien han trabajado dentro de la tradición semántica o, para usar una expresión de L. Bonjour, se han movido dentro de concepciones cuasiempiristas. Las visiones más cercanas a la concepción que estoy defendiendo son las de M. Friedman y A. Richardson, aunque el primero prefiere hablar de constitución semántica y el segundo de constitución de prácticas, donde yo prefiero hablar en un sentido más tradicional de constitución de la experiencia. Para una crítica de las posturas de Friedman y Richardson véase mi Reconsiderando a Friedman, Richardson y lo a priori constitutivo, en: Ideas y Valores, 131 (2006). Para una muestra comprehensiva de las concepciones contemporáneas de lo a priori, véase Boghosian, P.A. y C. Peacocke, New Essays on the A Priori, Oxford: Clarendon Press, 2000.
-
43 Esta tesis, defendida tempranamente por Cassirer, ha sido llamada por Thomas Mormann tesis de la identidad, aunque Mormann no considera el caso de la percepción. Véase su Idealización y matematización en el idealismo crítico de Cassirer, en: Txapartegi, E. (comp.), o.c.
-
44 Para una exposición detallada de estos conceptos véase Meserve, B., Fundamental Concepts of Geometry, Cambridge: Addison-Wesley Publishing Company, 1955; y Smart, J., Modern Geometries, Belmont: Brooks/Cole Pub. Company, 1994.
-
45 La expresión pertenece a H. Weyl. Véase su Filosofía de las matemáticas y de la ciencia natural, México D.F.: UNAM, 1965.
-
46 Klein, F., Elementary Mathematics from an Advanced Standpoint, Nueva York: The Macmillan Company, 1939, p. 133.
-
47 Para más detalles, véase Shepard, R., The Perceptual Organization of Colors: An Adaptation to Regularities of the Terrestrial World?, en: Barkow, J., L. Cosmides y J. Tooby (eds.), The Adapted Mind. Evolutionary Psychology and the Generation of Culture, Nueva York: Oxford University Press, 1992; Maloney, L.T. y B.A. Wandell, Color Constancy: A Method for Recovering Surface Spectral Reflectance, en: Journal of the Optical Society of America, III (1986), pp. 29-33.
-
48 Las transformaciones de Lorentz surgen en el contexto de las ecuaciones de Maxwell para el campo electromagnético. Dichas ecuaciones describen el comportamiento de dicho campo en cada punto del espacio y en cada instante de tiempo. Entonces surgió la pregunta: ¿se pueden cambiar la posición y el tiempo en las ecuaciones de Maxwell sin cambiar su forma? En el caso de las ecuaciones de la mecánica newtoniana, la respuesta es afirmativa debido al principio de relatividad de Galileo: se puede pasar de un sistema de referencia a otro sin cambiar la forma de las ecuaciones, si el tiempo medido en cada sistema es el mismo. En el caso del electromagnetismo, el problema es más complicado porque no se puede recurrir a la relatividad galileana. Sin embargo, Lorentz demostró que existe una transformación matemática que deja invariante la forma de las ecuaciones de Maxwell, siempre y cuando se cambie no solo la posición de un punto sino también el tiempo.
-
49 Para una elucidación profunda de estos temas, véase Friedman, M., Foundations of Space-Time Theories, Princeton: Princeton University Press, 1983.
-
50 CRP, A140-B179 (el énfasis es mío).
-
51 Ibid., A141.













