Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Areté
versión impresa ISSN 1016-913X
arete v.21 n.2 Lima 2009
ARTÍCULOS
El imaginario geométrico del hombre que delibera
. Esquemas de ejercicio de la φαυτασία βουλευτική en AristótelesThe geometric imagination of the deliberating man. Exercise schemes of the φαυτασία βουλευτική in Aristotle
Elisabetta Cattanei
Università degli Studi di Cagliari, Italia.
Resumen
El estudio parte de la discusión de De anima, III, 11, 434a7-10: a diferencia de las interpretaciones más difundidas del pasaje, que dependen considerablemente del comentario de Filopón, aquí se busca reconstruir la actividad de medición, planteada en relación de analogía con la "imaginación deliberativa", a la luz de procedimientos de descomposición y recomposición de figuras geométricas, muy difundidos en los siglos V-IV a.C., de los cuales se presentan también ilustraciones numismáticas. En la misma línea se puede situar tanto la referencia de Ética Nicomáquea, III, 5, 1112b20-21 al "análisis" de las figuras, como el de Ética Nicomáquea, VI, 9, 1142a23-29 al triángulo como "extremo". A este modelo metrético-espacial de la phantasia bouleutikē se añade uno de tipo logístico-temporal, que es mencionado en De anima, III, 7, 431b7-8 y en De memoria, 2, 453a15-16, con una interesante confirmación en Tucídides, I, 138, 3, donde Temístocles es comparado con un "habilísimo gnōmōn. En ambos casos, los modelos matemáticos en los que se inspira el hombre que imagina mientras trata de comprender qué es obrar bien, aquí y ahora, no son productos refinados de ciencia teórica, sino que pertenecen a aquellas "matemáticas de los mercaderes", que Platón desaconsejaba practicar para alcanzar la visión del verdadero bien.
Palabras clave: Aristóteles, deliberación, geometría, análisis,
έσχατουe
Abstract
The paper begins with the discussion of De anima, III, 11, 434a7-10:unlike the best known interpretations of the passage, which considerably depend on Philoponus commentary, here we try to reconstruct the measurement activity, presented in a relationship of analogy with the "deliberative imagination", in the light of procedures of decomposition and recomposition of geometrical figures, which were widely spread in the V-IV centuries B.C., of which numismatic illustrations are also offered. It is possible to understand in the same line the reference both to the "analysis" of figures in Nichomachean Ethics, III, 5, 1112b20-21, and to the triangle as an "extreme" in Nichomachean Ethics, VI, 9, 1142a23. To this spatial-metretic model of the phantasia bouleutikē, a logistic-temporal one is added, mentioned in De anima, III, 7, 431b7-8 and De memoria, 2, 453a15-16, with an interesting confirmation in Thucydides, I, 138, 3, where Themistocles is compared to a skillfull gnōmōn. In both cases, the mathematical models that serve as inspiration to the man that imagines while trying to understand what is to act well, here and now, are not refined products of theoretical sciences, but part of those "merchants mathematics" which Plato advised not to practice in order to gain the vision of the true good.
Keywords: Aristotle, deliberation, geometry, analysis, έσχατουe
1. La φαυτασία βουλευτική y sus esquemas de ejercicio
Hay un aspecto "fantástico" en la deliberación según Aristóteles. El proceso de bou¿leusij, o "deliberación", que consiste en la búsqueda y en la determinación de acciones individuales que sean medios para alcanzar un cierto fin, no parece ocurrir sin un aporte de la fanτasi/a: es decir, el hombre –que al razonar llega a establecer qué hacer, aquí y ahora, para obtener algo que se propone en la vida– debe también emplear la imaginación1.
La importancia de los roles que Aristóteles reconoce a la fanτasi/a, sea en la teoría del movimiento animal como en la de la acción humana, no se le ha escapado desde luego a los filósofos, que han prestado especial atención tanto a los lazos entre la imaginación y el deseo o "tendencia" (o)/recij) como motor de la acción, así como a las repercusiones que tales lazos tienen con la naturaleza humana y la estructura del razonamiento práctico2.
Los animales se mueven, y los hombres se mueven y actúan, cuando "buscan cosas vistas e imaginadas; no todas sino solo aquellas por las cuales, a causa de una necesidad, experimentan una tensión interior"3. Así, movimiento y acción presentan una "reactividad no al mundo simpliciter, sino a la visión que de él tiene el animal"4, producida en virtud de una actividad "crítica", de selección y distinción, a la que contribuyen sensación, imaginación y, allí donde exista, intelecto5.
También aquella que el De anima llama fantasi/a bouleutike/, "imaginación deliberativa"6, puede por lo mismo ser interpretada cuando menos como una presentación selectiva y discriminatoria a nuestra alma de imágenes de ciertas "cosas": las que vuelven al ámbito de la deliberación, es decir, acciones particulares y concretas, que apuntan a un determinado fin; el hombre, en otras palabras, se figura acciones distintas que pueden llevarlo a su objetivo y alcanza a "ver" cuál sería la mejor acción que puede llevar a cabo7. Esto lo hace el hombre, y solo el hombre: a diferencia de la fantasi/a ai)sqhtikh/, "la imaginación sensitiva", que "se encuentra también en los demás animales", la deliberativa pertenece "solamente a los animales dotados de razón (logistikoi=j)", porque "decidir si hacer esto o aquello es ya tarea del razonamiento (logismou= e)/rgon)"8. Por tal motivo, pues, por su cooperación con el logismo/j práctico, la imaginación deliberativa es –se lee siempre en el De anima– "racional" (logistikh/) y propia del hombre9. Ambas formas de fantasi/a –la racional y la sensitiva– constituyen aquello "sin lo cual" el animal no tiene la facultad de tender (o(rektiko/n) hacia algo ni, en consecuencia, la facultad de moverse a sí mismo hacia ese algo10. Y, sin embargo, únicamente la fantasi/a bouleutikh¿ tiene carácter racional y humano: un carácter que sin duda deriva del vínculo que tiene con el razonamiento que nos guía en la praxis, pero que también puede provenirle de un cierto modo de proceder, análogo al del "cálculo" práctico, si no emparentado con él11.
En efecto, ¿cómo funciona la imaginación deliberativa? ¿Es que se limita a seleccionar y distinguir datos para después transferirlos, separados entre sí, al intelecto que los conecta en un segundo momento, considerando las cosas que hay que hacer? Aristóteles dice muy poco a este respecto; sin embargo, de ese poco que sugiere surge una indicación de relativo interés: el ejercicio de la fantasi/a bouleutikh¿ se modela en esquemas que se remiten a procedimientos muy comunes de medición y descomposición de las magnitudes geométricas, no ignoradas por la geometría como ciencia teórica, sino compartidas por difusas aplicaciones de geometría empírica y "visiva"; y las actividades psicofísicas involucradas en estos procedimientos consisten en separar y discriminar figuras de figuras, en el curso de lo cual no se pierde una "visión de conjunto", lo que permite ponerlas en relación, confrontarlas, valorarlas, al apenas ser vistas.
2. "Medir con una unidad", "obtener una unidad a partir de más imágenes" (De anima, III, 11, 434a7-10)
A un esquema fundamental de ejercicio de la "imaginación deliberativa" –un esquema "metrético"– se alude al término de la afirmación de De anima, III 11, recordada hace poco, según la cual se trata de una forma de φαντασία que pertenece solo a los animales racionales, ya que se acompaña a aquella "obra del razonamiento" que consiste en establecer si se debe realizar una acción en lugar de otra. El argumento de Aristóteles parte de la consideración que los animales "imperfectos" (a)telw=n), provistos únicamente del sentido del tacto, se mueven, como los superiores, por causa del deseo y de la imaginación puesto que experimentan dolor y placer; en ellos, sin embargo, deseo e imaginación "están presentes de manera indeterminada" (a)ori/stwj d e)/nestin); tan cierto es esto que originan movimientos indeterminados12. En este punto, se lee la siguiente observación: "h( meìn ouån ai)sqetikhì fantasi/a, w(/sper ei)/rhtai, kaiì e)n toi=j a)/lloij z%/oij u(pa/rxei, h( deì bouleutikhì e)n toi=j logistikoi=j (po/teron gaìr pra/cei to/de h)ì to/de, logismou= h)/dh e)stiìn e)/rgon: kaiì a)na/gkh e(niì metrei=n: toì mei=zon gaìr diw/kei: w(/ste du/natai e(/n e)k pleio/nwn fantasma/twn poiei=n)"13.
El principal problema de traducción que conllevan estas líneas reside en una versión coherente del término e(/n en sus dos ocurrencias: en 1.8, es claro que Aristóteles hace referencia a "una unidad de medida", mientras que en 1.10, a lo más, se puede considerar que él tenga en mente "una única imagen", formada por muchas14.
Una de las traducciones italianas más acreditadas, por ejemplo, dice: "Limmaginazione sensitiva, come si è detto, si trova dunque anche negli altri animali, mentre la deliberativa soltanto in quelli forniti di ragione. Infatti, decidere se fare questo o quello è ormai compito del ragionamento, ed è necessario misurare con ununica cosa, poiché si persegue un bene più grande, e di conseguenza di più immagini si può formare una sola" (La imaginación sensitiva, como se ha dicho, se halla pues en los otros animales, mientras que la deliberativa solo en aquellos provistos de razón. En efecto, decidir si ha de hacerse esto o aquello es ya tarea del razonamiento, y es necesario medir con una única cosa, ya que se persigue un bien más grande y, en consecuencia, de más imágenes se puede formar una sola)15. Aquí, pues, se explicaría que "el hombre, con el razonamiento y el cálculo mental, elige los medios que parecen más adecuados para alcanzar el fin y el bien queridos. En tal elección o deliberación, él se sirve de un criterio que es justamente el de hallar los medios más idóneos para obtener el bien que considera mayor. De tal modo se demuestra capaz de sintetizar las diversas y posibles líneas de acción que ha imaginado, en una sola, y que es la que efectivamente se ejecuta"16.Esta reconstrucción, que converge con muchas otras, puede legítimamente suscitar dos interrogantes. En primer lugar, se considera del todo accesorio y vago remitirse a la medición con una unidad, lo que acaso Aristóteles lleva a cabo en un sentido y con intenciones bien precisas, dada la extrema escasez y la sorprendente precisión de todas sus alusiones al metrei=n y al gewmetrei=n en el ámbito de su reflexión psicológica y ética17; pero sobre todo, en el primer caso, se entiende e(/n como "unidad de medida", y entonces –en el sentido que explicaré mejor dentro de poco– como mínimo indivisible respecto de algo "más grande" que se quiere medir; mientras que en el segundo caso e/(n parecería él mismo algo "más grande", obtenido de la "síntesis" de la multiplicidad de phantasmata.
En todo caso, parecería más oportuno atenerse ambas veces al primer significado que e(/n asume al interior del pasaje, el de "unidad de medida", tanto más en cuanto que los comentaristas muestran un amplio consenso para referir el "e(niì metrei=n" de 434a8-9 a la teoría de la unidad de medida, que se encuentra en el primer capítulo del libro Iota de la Metafísica18.
Si cumple el papel de "unidad de medida", el "uno" sostiene con la cosa medida una relación bien precisa, que permite asir con mayor exactitud, sea la relación entre "e(niì" y "toì mei=zon" en las líneas 8-9, sea aquella entre "e(/n" y "e)k pleio/nwn fantasma/twn" en las líneas 9-10.
La unidad de medida antes que nada permite "conocer" el género de cosas del que es medida, y en particular conocer sus aspectos cuantitativos, es decir, saber "a cuánto asciende" una determinada cosa, "cuánto vale" y "qué tan grande es"19. Cada unidad es de la misma especie de aquello que mide –de ahí que una línea mida una línea, una superficie una superficie, un peso un peso, etc.–; sin embargo, existe un modelo de unidad de medida –que todas imitan–20 constituido por la mónada menor respecto al número21. En efecto, sabemos que aquel determinado grupo de cosas es, por ejemplo, de cuatro cosas cuando llevamos sus componentes a cuatro unidades, y esto vale para el número en cuanto tal, que por definición es "pluralidad compuesta de mónadas"22. Pero la mónada está en condiciones de desarrollar de manera perfecta y exactísima su función de medida porque presenta determinadas características esenciales: es "indivisible bajo todos los aspectos"23, es decir, "simple" según la calidad y la cantidad24; y es "aquello de lo cual resulta visiblemente imposible sustraer o añadir algo"25, un mínimo en que se detiene la división y que puede crecer solo por iteración26. Las unidades de medida de otro género no son de por sí indivisibles, simples en la cantidad y en la cualidad, ni incapaces de sufrir aumento o disminución como las mónadas, pero sí son usadas y puestas como tales por quien procede a la medición: "incluso entre las líneas –que en tanto continuas son divisibles al infinito– usan la línea de un pie como indivisible"27 y "todos consideran como medida –sea de líquidos o de sólidos, sea de un peso o de una magnitud– eso primero de lo que no es posible, según la sensación, sustraer y quitar algo"28; o sea, una cantidad mínima de líquido, sólido, peso o magnitud –o también de movimiento y de sonido– que de por sí es susceptible de aumento o disminución, pero cuyo aumento o disminución, a diferencia lo que sucede con las cantidades mayores, más difícilmente "podría escapar" a nuestros sentidos29.
Medir con una unidad significa por ello aplicar la unidad un determinado número de veces a la cosa sujeta a medición, y agotarla en un determinado número de unidades, obteniendo como resultado el número de cuantas unidades a las que ella ascienda, el número de unidades que ella "valga"; medir consiste, pues, en reducir lo más grande al mínimo mediante una progresiva comparación y balanceo entre mayor y menor, exceso o defecto30. No por casualidad Filopón, comentando 434a8-9, elige como ejemplo la aplicación del cubo, por parte de un arquitecto, a las vigas de madera a su disposición, que son medidas exhaustivamente, estableciendo cuáles son más grandes y cuáles más pequeñas31.
El ejemplo del cubo –más allá del uso poco diestro que de él hace Filopón–32 resulta muy feliz, y no solo porque es explícitamente citado por Aristóteles en Metafísica, Iota, 133. Se trata de una unidad de medida de la longitud, es decir, de las cantidades más simples que tienen naturaleza continua34: "medir con un cubo" significa, pues, medir un continuo, y el carácter de continuidad y divisibilidad es lo que Aristóteles trae a colación para justificar la aplicación de determinaciones cuantitativas –como exceso, defecto y medio– a las acciones35. Se puede, así, legítimamente imaginar "medir con una unidad" las acciones que de por sí no son cantidades pero sí movimientos, en virtud de su propiedad de ser continuas; pero esto implica que su "unidad de medida" –admitiendo que la hubiera– será entendida en analogía con la de las líneas, que es precisamente el cubo, o de las otras cantidades continuas, como lo son por ejemplo las superficies rectilíneas, cuya unidad está constituida por el triángulo36 y los sólidos. Además, la referencia al cubo no solo permite comprender cómo la geometría usa una unidad de medida establecida, sino también cómo la explora: en efecto, es notable y muy antiguo el problema de la "división del cubo", que remite a la búsqueda de una unidad de medida común entre dos líneas mediante el método de la "sustracción repetida y recíproca"37. Descrito brevemente en su forma más simple, este método consiste en medir dos segmentos de recta de diferente longitud sustrayendo el más pequeño del más grande un determinado número de veces; si de la sustracción no queda nada, evidentemente el segmento más pequeño es unidad de medida; si más bien produce un resto, se usa este resto como unidad de medida de los dos segmentos de partida, sustrayéndolo de ambos un determinado número de veces; la misma operación se repite, recurrentemente, para cada resto obtenido, que es siempre más pequeño, hasta que no se halle uno que esté un número preciso de veces en los dos segmentos de partida, midiéndolos exhaustivamente: este último será la unidad de medida común de los dos segmentos, siempre que ellos tengan una, o sea, que sean conmensurables38.
Según este modelo de medida basado en la sustracción, la cosa que se mide es siempre mayor, o más grande, que la unidad, puesto que debe contener una cantidad –lo más exactamente posible– de unidades, en las cuales se descompone, durante el proceso de medición. "Lo que es más grande", y que observa el hombre que delibera e imagina al mismo tiempo, se presenta pues como algo de lo que se llega a conocer a cuánto asciende o cuánto "vale", de por sí en relación a otro, gracias al hecho de que se compone de un determinado número de unidades, llegando a las cuales se detiene su proceso de descomposición39.
Pero entonces, dentro de este marco conceptual que no se ve por qué deba cambiar en el curso de unas pocas palabras, "las muchas imágenes" a partir de las cuales en II. 9-10 se dice que el mismo hombre puede obtener como resultado un e(/n, se presentan no tanto como imágenes independientes entre sí que son combinadas en una unidad más grande producida por síntesis, sino más bien como porciones en las que "lo que es más grande" es descompuesto hasta hallar –por análisis, no por síntesis– la unidad de medida, el extremo en el cual hay que detener su proceso de división y por cuyo medio se llega a conocer el monto, el valor y el orden del complejo de sus partes.
Las líneas donde se señala el modo como un hombre imagina mientras delibera pueden pues ser vertidas así: "En efecto, decidir si él hará esto o aquello es ya tarea del razonamiento práctico, y es necesario medir con una unidad de medida: efectivamente, él observa al más grande, de modo que puede obtener una unidad de medida a partir de muchas imágenes".
"El más grande", al que cada uno de nosotros observa, puede ser imaginado como una determinada extensión, por ejemplo como el área total de una figura limitada por un determinado perímetro, y puede ser entendido, adecuadamente, como la representación del final de nuestras acciones, que es sometido, mediante la deliberación, a un proceso de "análisis"40; pero también los primeros resultados de este análisis, las partes más amplias en las que se descompone el entero, que representan los medios o las acciones de naturaleza más genérica para obtener el fin, son, a su vez, sometidos a análisis, hasta ese mínimo indivisible –la acción que se debe realizar aquí y ahora– que es el justo "metro", al cual llevar el complejo de fines y acciones sobre el que estamos razonando41.
3. "Investigar y analizar como se hace con una figura geométrica" (Ética Nicomáquea, III, 5, 1112b20-21), advertir la sensación "con la que percibimos que, entre los entes matemáticos, el triángulo es un extremo" (Ética Nicomáquea, VI, 9, 1142a23-29)
Leído de la manera como se ha hecho, el esquema "metrético" según el que procede la "imaginación deliberativa" halla correspondencia y ejemplificación en un lugar del tercer libro de la Ética Nicomáquea, que a menudo es traído a colación para ilustrar su funcionamiento: un funcionamiento que se modela explícitamente en un esquema de tipo geométrico, vinculado al análisis de las figuras42.
Aristóteles precisa que nosotros "deliberamos no sobre los fines sino sobre lo que conduce al fin", como por ejemplo un médico no delibera sobre curar a un enfermo, sino sobre cuánto está en su poder hacer para ejecutar con éxito tal objetivo, es decir, sobre las acciones terapéuticas que concretamente puede realizar, aquí y ahora, para devolverle en verdad la salud43. Los médicos –y todos aquellos que deliberan– desarrollan pues una "indagación"44: en general, "planteado el objetivo, indagan sobre cómo llegar a él y a través de qué medios"45, pero más en particular, si resulta que es posible conseguirlo de diversas maneras, indagan "cuáles son las más rápidas y bellas"46; o si puede ser obtenido de un solo modo, buscan "cómo sucederá a través de él y él a través de qué cosa, hasta que no lleguen a la causa próxima" –o sea, a la acción más cercana al efecto–, "que es la última en el orden del descubrimiento"47. Teniendo fijado su objetivo –la salud del enfermo–, el médico se plantea diferentes líneas de acción que puedan llevarlo a cabo, las confronta y selecciona las más eficaces; o bien puede seleccionar una sola, que descompone en acciones individuales, como los eslabones de una cadena, hasta descubrir la acción correspondiente al último eslabón, que elige ejecutar, ya que considera que podría producir inmediatamente el efecto deseado.
Quien delibera se comporta de manera análoga a la del arquitecto de Filopón: quiere realizar concretamente algo; tiene a su disposición una serie de instrumentos: no vigas de madera de dimensiones diversas, sino otras realidades –como se decía– dotadas del carácter de la continuidad, es decir, acciones diferentes; las compara y las selecciona. Pero no se queda aquí: procede a descomponerlas en verdaderos "segmentos" hasta descubrir uno, extremo, en el que decide detenerse desde el momento en que le permitirá realizar lo que se había propuesto48.
En consecuencia, cuando delibera, el hombre somete las acciones que debe realizar a una indagación (zh/tesij), que es una suerte de análisis (a)na/lusij), "viéndolas" por ello de cierto modo, representándoselas según un esquema determinado. "Quien delibera parece indagar y analizar
(a)nalu/ein) en el modo mencionado, como se hace con una figura geométrica
(w(/sper dia/gramma). Es evidente que no toda indagación es una deliberación, como no lo son las indagaciones matemáticas, mientras que cada deliberación es una indagación, y el último paso en el análisis (toì e(/sxaton e)n t$= a)nalu/sei) es el primero en la realización (t$= gene/sei)"49.
Aristóteles tiene en mente, como término de analogía, un procedimiento, seguido por los matemáticos en sus pesquisas, que consiste en "analizar un diafragma" hasta hallar un "extremo en el análisis"; este procedimiento de "análisis matemático" se perfila como un método más zetético que apodíctico, y se aplica a la ilustración gráfica de las figuras, es decir, a los dibujos geométricos50.
La referencia más eficaz para comprender de qué pueda tratarse no tiene que ver tanto con el "analizar" (to a)nalu/ein) citado en el primer libro de los Analíticos segundos, 78a7-8, donde se alude –siempre con una explícita conexión con las matemáticas (78a11)– a un procedimiento demostrativo propio de la geometría, por el cual, a partir de las preposiciones que forman las definiciones, es decir, como dirá Papo, "suponiendo que está probado lo que se investigaba", se remite a la proposición antecedente, y a la antecedente de la antecedente, "hasta que, retrocediendo de este modo, llegamos a algo más destacado o que tiene la posición de principio"51.
Más que en otros lugares, y más que en la silogística, un paralelo del "análisis de los diagramas", puesto en relación de analogía con la deliberación puede ser hallado en el libro noveno de la Metafísica, donde Aristóteles explica que "en los diagramas se hacen descubrimientos mediante el acto, ya que hacen descubrimientos –y el sujeto son los geómetras que los dibujan– dividiéndolos"52.
Los ejemplos propuestos, expresados en forma muy sintética, son dos: que "el triángulo sea dos rectos" –es decir, que la suma de sus ángulos sea igual a dos ángulos rectos–, y que el ángulo "al interior de un semicírculo sea universalmente recto" –o sea, que todos los ángulos inscritos en un semicírculo son rectos53–. Ahora bien, la pertenencia de estas propiedades, respectivamente, a los ángulos internos de un triángulo y a los ángulos inscritos en un semicírculo, resulta "manifiesta"54, y es captada porque aparece "de pronto clara para quien la ve (i)do/nti)"55: para quien ve un diagrama sometido a una determinada división.
En el primer caso (fig. 1), se advierte al primer vistazo la igualdad de los ángulos internos del triángulo ABC con los tres ángulos "en torno a un punto" (C)56, que termina dividiendo dos rectas: se trata de uno de los vértices de la base del triángulo, que corta la prolongación de la base (BC, CD) y la "paralela al lado", oportunamente "trazada hacia arriba" (CE)57.
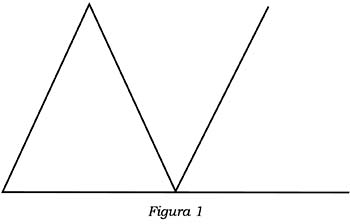
Para los ángulos en torno al punto C, se hacen efectivamente evidentes las propiedades de igualdad de los ángulos formados por líneas (AC, BD) que cortan dos rectas paralelas (AB, CE): la recta AC forma los ángulos alternos iguales BCA y ACE; la recta BD forma un ángulo externo ECD igual al ángulo opuesto interno ABC; pero dado que el ángulo ACE es igual a BAC, todo el ángulo externo ACD resulta igual a los dos ángulos internos opuestos BAC y ABC; si se añade el tercer ángulo interno ACB al ángulo externo ACD y a los dos ángulos internos BAC y ABC, se advierte inmediatamente que ACB + ACD, que es igual a dos ángulos rectos, es igual a ACB + BAC + ACB, es decir, a la suma de los ángulos internos del triángulo ABC58.
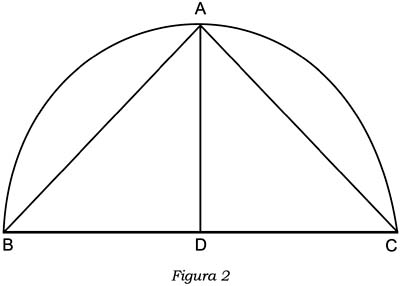
En el segundo caso (fig. 2), se obtiene el resultado dividiendo la base del semicírculo BC –y, por tanto, todo el semicírculo– en dos mitades (BD, DC), ya que se traza la perpendicular al centro (AD)59. "¿Por qué el ángulo en un semicírculo es invariablemente un ángulo recto? Porque ―así Heath resuelve las palabras de Aristóteles―, si llegara a haber tres líneas rectas, dos que forman la base (BD, DC), y la tercera dispuesta en ángulo recto en su centro (AD), el hecho resulta obvio en virtud de una simple inspección (by simple inspection) por parte de quien conoce la propiedad a la cual se nos refiere", es decir, "la propiedad que poseen los ángulos de un triángulo de ser iguales a dos rectos, mencionada dos líneas arriba"60.
En otras palabras, si se traza una perpendicular (AD) al centro de la circunferencia del semicírculo, y se obtiene así dos triángulos rectángulos isósceles (ABD, ACD), se halla que cada uno de los ángulos en el centro (ADB, ADC) asciende a la suma de dos ángulos, respectivamente DBA + DAB y DCA + DAC; pero cada uno de estos cuatro ángulos asciende a un cuarto de la suma de los ángulos del triángulo más grande (ABC), es decir, a medio ángulo recto; pero entonces, ADB y ADC son cada uno iguales a un ángulo recto61.
Los geómetras, en ambos casos ilustrados, "conocen produciendo"62, y su poiei=n puede entenderse como un "analizar diagramas", ya que consiste en dividir o descomponer figuras, trazando –con la línea y el compás– líneas que dividen líneas y superficies en determinados puntos: puntos en los cuales uno se detiene porque en ellos "quien observa" percibe visiblemente, y de ese modo "descubre" o "halla" una determinada propiedad de las figuras dibujadas, que era objeto de indagación63.
La indagación para el análisis de un extremo en el que se detiene la descomposición de un diagrama pertenece a una geometría "visiva" de base constructiva, que cronológicamente precede al desarrollo de la geometría teórica y científica, organizada deductivamente para acciones y teoremas; empero, la una queda fuertemente vinculada a la otra, aun en el edificio de los Elementos de Euclides, pese al notable esfuerzo teórico de separarlas, de lo cual se hizo cargo en primer lugar Platón64.
Aristóteles considera a las prácticas visivas y constructivas –de las cuales documenta su amplia difusión– como un auxilio indispensable para la geometría científica, que no es mellada, en el rigor y en la verdad de sus demostraciones, por el uso de líneas trazadas en la arena o de figuras dibujadas y construidas65. Por esta razón hace que el análisis de los diagramas recaiga entre las "investigaciones matemáticas" y, si bien la compara con la indagación desarrollada por quien delibera, se preocupa de subrayar que "no toda indagación es una deliberación, y las indagaciones matemáticas no lo son"66. A menudo, en efecto, él subraya que la ética y las matemáticas son diferentes y que se mantienen autónomas, fundamentalmente porque tienen objetos, principios y métodos diversos, dado que la una trata de cosas particulares, variables, contingentes, vinculadas al placer y al dolor –las acciones y los comportamientos del hombre–, mientras que la otra vierte sus entidades eternas, inmóviles, necesarias, incorruptibles: el triángulo y sus ángulos, el cuadrado y su diagonal67. Aunque no es raro, aspectos de las matemáticas de su tiempo, sobre todo de carácter paracientífico u obsoleto, le sirven a Aristóteles al menos como términos predilectos de comparación, y hasta como material terminológico, conceptual y argumentativo de recuperación para ilustrar y explicar realidades éticas e incluso psicológicas68.
No por casualidad, a la luz de los procedimientos de la geometría visiva y constructiva, otro pasaje de la Ética Nicomáquea, considerado por no pocos intérpretes fuera de lugar o irrelevante, llega más bien a constituirse en una descripción eficaz del último acto del trabajo "metrético" y "geométrico" al cual se dedica nuestra imaginación mientras deliberamos: es el momento final en que la fantasía y la deliberación ceden el paso a la sensación69.
Aristóteles está hablando de la sabiduría que, como se sabe, es la virtud de la facultad "calculadora" del alma racional: aquella antepuesta a la praxis, aquella con la que el hombre delibera70. Su argumento se condice con la naturaleza de "extremo" (e(/sxaton) propia del "objeto de la praxis" (prakto/n), que determina la distinción entre la sabiduría, de una parte, y la ciencia y el intelecto, de la otra: el intelecto se dirige a las definiciones, no sujetas a demostración, mientras que la sabiduría "tiene por objeto aquel extremo del cual no se produce ciencia sino más bien sensación (aiãsqhsij)"71. El "extremo" al que alude Aristóteles consiste justo en el término último de la cadena deliberativa, que es elegido y actuado; pero la cosa aquí más interesante es cómo se describe la "sensación" del extremo: "No la sensación que tiene que ver con los sensibles propiamente dichos, sino más bien aquella con la que percibimos que, entre los entes matemáticos, un triángulo es un extremo (e(/sxaton), dado que también en ese aquí uno se detiene"72.
El "extremo" en el que se detiene la deliberación es percibido sensiblemente, pero no como la vista ve un color o como el oído oye un sonido; se lo percibe como un triángulo: en efecto, un triángulo, en tanto figura, es un sensible común, no un sensible propiamente dicho73. Y, sin embargo, no es percibido como una figura cualquiera, como un triángulo cualquiera, como un acto cualquiera de "sentido común"; el acto perceptivo de sentido común, que lo aprehende, se escapa del punto en que se detiene un proceso de descomposición, análogo al operado "entre los entes matemáticos": la descomposición de superficies en superficies o, más en general, de magnitudes de una determinada especie en magnitudes de la misma especie (sólidos en sólidos, líneas en líneas, pesos en pesos, etc.) hasta un "extremo", constituido por la magnitud más simple en su especie; y entre las superficies rectilíneas –como Aristóteles recuerda también en Metafísica, Iota, I– el "extremo" en el que se detiene su descomposición coincide con la superficie triangular74.
Se señalaba antes que, gracias a operaciones de este tipo, los matemáticos indagan desde la época arcaica las unidades de medida, al interior de cada especie de magnitud y de cantidad; pero la operación, siempre de tipo constructivo y "visivo", retomada aquí por Aristóteles, es más precisa: se trata de la triangulación de las áreas, practicada ya en el antiguo Egipto con fines de medición, especialmente en la agrimensura y en la geodesia aplicadas al delta del Nilo, que consiste en la descomposición de un área en una red de triángulos adyacentes, que no admiten ulteriores fraccionamientos más allá de un determinado triángulo75.
Existen aplicaciones muy conocidas de la triangulación al interior de la resolución de problemas geométricos y, acaso, en la memoria de Aristóteles estaba presente la tercera parte del experimento mayéutico del esclavo en el Menón de Platón, donde se encuentra un ejemplo significativo de ello76. En el contexto de una discusión que aborda también la naturaleza de la virtud y la ciencia, Sócrates induce al esclavo a cambiar de método de indagación luego de que ha fracasado en su intento de determinar aritméticamente la medida de un cuadrado doble respecto a un cuadrado dado que tiene un lado de dos pies de largo77. Sócrates invita al joven a construir (fig. 3) un cuadrado cuádruplo (AEGI) respecto al de partida (ABCD), y después a dividirlo en ocho triángulos, logrando ver el cuadrado doble, formado por cuatro triángulos (BDHF), y a indicar su lado (BD) que coincide con la diagonal del cuadrado dado78. El "diagrama", producido y analizado por Sócrates y por el esclavo, resulta ser el siguiente:
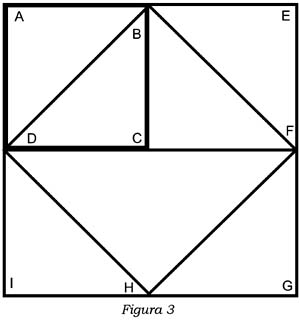
El esclavo termina su indagación de una medida –aritméticamente indefinida– de la diagonal del cuadrado de partida, porque, mediante la reducción de una superficie más grande a un retículo de superficies triangulares, ve un único triángulo en el que se detiene: su lado es el largo, la diagonal que está buscando; con un acto perceptivo del mismo tipo, el hombre que delibera –y lo puede hacer solo en casos "que no se sabe cómo terminarán y en aquellos en que hay algo indeterminado"79– percibe sensiblemente un extremo: el prakto/n, qué hacer aquí y ahora. Por lo demás, como los geómetras, que obtienen conocimientos analizando las figuras y descomponiéndolas en unidades, pone fin a su indagación, luego de que, con la fantasía, ha analizado, descompuesto y medido los fines que debe perseguir, las acciones que debe realizar.
4. "Calcular y deliberar, como si se las estuviera viendo, las cosas futuras en relación a las presentes" (De anima, III, 7, 431b7-8), "recurrir a la memoria" como "indagación de una imagen en un sustrato corpóreo" no afectado por la melancolía (De memoria, 2, 453a15-16).
En los pasajes que hasta aquí se ha examinado Aristóteles usa, para sugerir algo sobre los modos de proceder de la fantasi/a bouleutikh/, esquemas de referencia que, en tanto "metréticos" y "geométricos", presuponen el carácter de continuidad de aquello a lo que se aplican: un carácter que, como se señalaba, funda de hecho la analogía entre el mundo de la praxis y el mundo de la geometría, ya que las acciones y las magnitudes comparten tal propiedad80.
Desde otro punto de la reflexión del De anima sobre la imaginación propia de los animales racionales81 –un punto precedente a aquel que se ha discutido al inicio– emerge, empero, la pauta de un esquema de referencia no tanto de tipo "metrético-espacial" como de tipo "logístico-temporal", donde el término "logístico" remite al "arte del cálculo" (logistikh/) dominante en la segunda mitad del siglo V a.C., que consistía en establecer relaciones (lo/goi) entre unidades diversas y series ordenadas de estas relaciones82.
Las dos tipologías de esquemas no son incompatibles, ni siquiera en sus ascendencias técnicas, porque la "metrética" basada en la sustracción podía ser expresada numéricamente mediante las cadenas de relaciones entre números, estudiadas por la "logística"83. Si bien la segunda tipología, explicitando las coordenadas de tiempo dentro de las que se sitúan la deliberación y la fantasía que la acompañan, inserta en el continuum de su proceder elementos de discriminación entre las partes, que requieren la institución de una relación de las unas con las otras: las unidades en que se descomponen los fanta/smata de quien delibera son distintas por lo menos desde el punto de vista temporal, y por eso hay que, oportunamente, vincularlas34. En efecto, son "cosas futuras en relación con las presentes", como Aristóteles observa: " con las imágenes y los pensamientos que se hallan en el alma como si las viese (w(sper o(rw=n), uno calcula y delibera las cosas futuras en relación con las presentes (logi/zetai kaiì boule¯uetai taì me/llonta pro/j taì paro/nta): y en el caso que se diga que allí se halla lo agradable o lo doloroso, al punto lo rehúye o lo persigue: en general es así en la praxis"35.
La "visión fantástica" que tiene lugar, cuando pensamos e imaginamos en el curso de la deliberación, que es un proceso para el cual se requiere tiempo y calma36, no se limita a formar una "red" de figuras más pequeñas que componen figuras más grandes, sino que se insertan en una red de relaciones entre cosas diversas: ante todo, entre cosas presentes y cosas futuras; "descomponer" hasta el extremo algo más grande se vincula así, explícitamente, a una actividad psíquica de conexión e interrelación entre las partes descompuestas.
Estas operaciones psíquicas de conexión se extienden también al pasado, no solo al presente y al futuro, pero solo si el pasado se hace presente37. Y esto es posible mediante aquel tipo de "silogismo" y, una vez más, de "indagación", en que según Aristóteles consiste la anamnesis o el "recurrir a la memoria": facultad propia solo del hombre en cuanto delibera, ella puede ser entendida –análogamente a la deliberación– como "una especie de silogismo"
(sullogismo/j tij), porque quien apela a la memoria recupera mediante una serie de pasajes y asociaciones, similares a los de un razonamiento concatenado "que ha visto u oído algo, o que ha advertido una determinada sensación"38. No obstante, su "desarrollo de silogismos" no se identifica con una pura actividad intelectual, sino con "la indagación de una imagen (zh/thsij... fanta/smatoj) en el sustrato corpóreo"39: no es casualidad que uno se pueda aplicar con la mente a traer algo a la memoria sin tener éxito, o bien sujetos en condiciones somáticas de profunda agitación ―como lo son los melancólicos― no logran fijar ninguna imagen que pueda servirles para suscitar a otra90; en general, además, el exceso de bilis negra que provoca la melancolía produce movimientos de la imaginación de intensidad anormal, capaces de transmutarse, durante el sueño, en visiones oníricas monstruosas y desordenadas91.
A condición de no ser melancólicos, se puede entonces desarrollar silogismos e "indagar silogísticamente", con el cuerpo, mediante "imágenes". Por cierto, el cuerpo es un cuerpo humano: los demás animales no tienen esta facultad; y se trata de un cuerpo humano saludable, no afectado por desequilibrios orgánicos. Sin embargo, en el hombre sano, también el mundo físico de las imágenes –y es claro ejemplo de esto el caso de la anamnesis– admite concatenaciones e indagaciones de "tipo silogístico", así como las admite el mundo del razonamiento del cual es citado como ejemplo propio la deliberación92; y no es pues un caso que la misma patología en condiciones de inhibir el "silogizar por imágenes", la melancolía, comporte la incapacidad de deliberar, unida a un exceso de deseo, que se expresa en el e)/qoj del intemperante93.
Pero entonces, así como en concreto es bastante difícil realizar un acto de "imaginación deliberativa" sin recurrir a experiencias pasadas, que las haga presentes y nos permita llevarlas a acciones futuras, tal vez el modelo de indagación propio de la anamnesis, "silogístico" pero somático, y declaradamente afín a la bou/lesij, puede servir bien para comprender mejor en qué sentido "descomponer" y "analizar diagramas" que acompaña a esta última implique también "calcular relaciones", o, sobre todo, para comprender la naturaleza psicofísica, corpórea y al mismo tiempo "más bien intelectual", de todas estas operaciones en su complejo.
5. Temístocles, "habilísimo gnōmōn con deliberación fulmínea" (Tucídides, I, 138, 3)
La práctica de las operaciones deliberativas ensalza a sus héroes: en el desarrollo de la propia concesión de "cálculo práctico" y de hombre sabio, Aristóteles se alinea a una tradición que reconoce la excelencia de Temístocles94. La ilustración por parte de Tucídides de las "dotes naturales" que él "había demostrado poseer en grado sumo", resultando "más que otros digno de admiración por este aspecto", señala una que suscita una notable curiosidad: la capacidad extraordinaria de deliberación de Temístocles es un signo de su naturaleza "gnomónica". Escribe Tucídides: "De hecho, en virtud de su natural inteligencia, a la que no había provisto con el estudio ni ninguna preparación preliminar, ni incrementos sucesivos, era un habilísimo gnomon (kra/tistoj gnw/mwn), con deliberación fulmínea (di e)laxi/sthj boulh+=j), de las situaciones que había que afrontar al instante, y era muy bueno, en general, para conjeturar cuál de las cosas inminentes (tw=n me/llontwn) estaban por verificarse. Era capaz de explicar lo que caía en el ámbito de su experiencia, pero no eludía juzgar también aquello de lo que no tenía experiencia directa, y lo hacía de modo adecuado; era capaz de prever lo mejor y lo peor cuando no eran visibles. En suma, por sus dotes naturales y por su rapidez de ejercicio (mele/thj deì braxu/thti), él fue habilísimo para conjeturar lo que fuese cada vez apropiado"95.
De este pasaje se han propuesto diferentes y autorizados comentarios que subrayan, entre otras cosas, cómo el uso de gnw/mwn para indicar una actividad de "juicio", la de un krith/j, es más bien raro y difícilmente casual96.
Literalmente, el "gnōmōn" constituye un instrumento de medición, usado por la astronomía arcaica para medir el tiempo y construir las meridianas, que en seguida es aplicado a la medición de las áreas; en este segundo caso, coincide con una figura plana, doblada como un codo, cuya forma recuerda a una gamma mayúscula (G), que es oportunamente añadida a la superficie por medir, entre las cuales se buscan relaciones precisas de semejanza97. En sus aplicaciones elementales, también el método del "gnōmōn", como el de la triangulación, pertenece a la "geometría visiva" y "constructiva", y resulta que además de una difusión muy vasta, ha tenido además una evolución teórica notable a la que alude el mismo Aristóteles98. El Menón de Platón, siempre en lo concerniente al "experimento del esclavo", contiene una ejemplificación que, sobre todo, y según algunos intérpretes, corresponde a la primera etapa de un procedimiento igualmente difuso y estudiado: el de la "sustracción recíproca y repetida", aplicado al lado y a la diagonal del cuadrado99. Como último intento de determinar aritméticamente la longitud del lado del cuadrado de área doble respecto al cuadrado dado que tiene el lado de dos pies de largo (fig. 4: ABCD), Sócrates le propone al muchacho que indique un valor "mayor de dos pies, pero menor de cuatro"100; después de haber respondido "tres pies"101, Sócrates convence al joven de haber indicado erróneamente el lado de un cuadrado de área nueve, y no de área ocho, mediante la aplicación al cuadrado de partida de un gnōmōn, cuyo lado menor es de un pie (BE,DG), es decir, la mitad (AE, EB) del lado (AB) del cuadrado de partida:
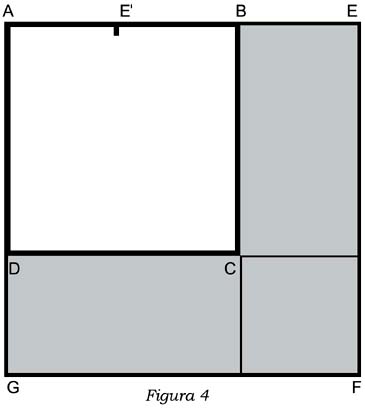
La medición gnomónica, en suma, pertenece en sus manifestaciones de base al mismo tipo de geometría de los procedimientos metréticos, de análisis y de "cálculo", a los cuales Aristóteles alude, allí donde habla de la "imaginación deliberativa"; no solo eso: su práctica históricamente parece vincularse, hasta sobreponerse, con estos procedimientos102. "La deliberación fulmínea", que Tucídides atribuye a Temístocles, evoca ella misma a un metrei=n, a un gewmetrei=n, y también a un logi/zesqai, en cuyo ejercicio él se demostró muy rápido, sin necesidad de conocimientos teóricos previos, destacando sobre todo en una actividad: una penetrante visión de las situaciones presentes, una eficaz previsión de los eventos futuros y de las "cosas que hay que hacer" (taì de/onta)103.
6. Moneda corriente
Si bien la habilidad gnomónica de Temístocles reposa en excepcionales dotes naturales de inteligencia y previsión, no hace falta pensar en ella ni en aquellos que han visto en los esquemas matemáticos de la "imaginación deliberativa" pensada por Aristóteles como refinados instrumentos teóricos de difícil aprendizaje, capaces de poner a prueba a las mentes más brillantes104. Pensando en la distinción que Sócrates hace con gran claridad en el Filebo entre las matemáticas "de los más" y las " de los filósofos"105, los modelos que se han visto de medición con una unidad, de análisis de los diagramas, de triangulación y de institución de "relaciones" entre unidades diversas, recaen sin duda en la primera categoría: una categoría que, en la República, Sócrates llama también "banáusica" y "rudimentaria", así como lo son los artesanos y los mercaderes que se sirven de "técnicas" allí comprendidas106.
En efecto, ¿dónde se puede encontrar ilustraciones originales y concretas de los esquemas matemáticos a los que Aristóteles se remite? Más que en cualquier otro lado, y con una difusión impresionante, en la moneda corriente; aquella "medida universal del valor", a la que se le ha reconocido un papel no secundario de "innovación mental" en el desarrollo de diversas formas de pensamiento racional y positivo entre los griegos107.
Por ejemplo, en el reverso, respectivamente, de dos diversas estateras de Egina (fig.5 y fig. 6), en cuyo anverso aparecía una tortuga (470-450 a.C.) se podía ver, acuñadas, las figuras de un cuadrado dividido en dos triángulos, que tenían como lado la diagonal, al interior de una construcción gnomónica:


Más simplemente, en el reverso de un tetradramo de Siracusa (510-500 a.C.), que presenta en el anverso una cuadriga al paso (fig. 7), se encuentra –como en muchísimas otras monedas también más recientes– un cuadrado dividido en cuatro cuadrados:

Pero entre los motivos más difundidos en el espacio no menos que en el tiempo, se encuentra un cuadrado dividido en triángulos, acuñados alternativamente (fig. 8), como aparece en esta dracma calcídica de Imera (520 a.C.):

¿De qué cosa, pues, tiene necesidad el imaginario geométrico del hombre que delibera para formarse? No requiere de grandes esfuerzos de aplicación, ni de un fino ejercicio intelectual, ni de conocimientos teóricos previos: de las descomposiciones de figuras sobre las que se modelan sus fanta/smata, mientras razona sobre lo que debe hacer, él puede tener experiencia empírica de manera cotidiana. Evidentemente, para que esta experiencia dé frutos se requiere de buenas condiciones psicofísicas y, en particular, no hay que ser melancólicos: los efectos de un exceso de bilis negra –que son somáticos, psíquicos y éticos al mismo tiempo– contrastan con la capacidad de evocar imágenes, o también con la de imaginar visiones ordenadas, no menos que en el poder de deliberar con eficacia. Pero en buenas condiciones de salud, los esquemas de medición, de análisis y de cálculo que para Aristóteles contribuyen mediante la fantasía a orientarnos en la praxis, no imponen de ninguna manera liberar "el ojo del alma" –como pedía Platón a las dia/noiai matemáticas– del "bárbaro pantano" del devenir, de la sensibilidad y de la vida cotidiana; todo lo contrario: más fácilmente que en otros lugares se puede encontrar ilustraciones de ello en aquellas bodegas y en aquellos mercados que Platón desaconsejaba vivamente frecuentar, a fin de aprender artes geométricas y de cálculo, que permitieran "ser un hombre" y tener una "visión del bien"108.
Traducción del italiano de Renato Sandoval Bacigalupo
-
Los principales pasajes de referencia sobre esta forma de "fantasía" en Aristóteles son: De anima, III, 7, 431b7-10; 11, 434a5-10. Sobre la "deliberación" en Aristóteles, ver: Natali, C., La sagezza di Aristotele, Nápoles: Bibliopolis, 1989, pp. 177-182.
-
Cf
. Nussbaum, M., The Fragility of Goodness. Luck and Ethics in Greek Tragedy and Philosophy, Cambridge: Cambridge University Press, 1986 (traducción al italiano de M. Scattola: La fragilità del bene.
Nussbaum, M., La fragilità del bene. Fortuna ed etica nella tragedia e nella filosofia greca, p. 511.
Ibid
Cf
Cf
Como la comunidad científica señala, no es simple deducir de lo que dice Aristóteles, especialmente en el libro III de De anima, una teoría orgánica y general de la "fantasía", que parece más oportuno considerar no tanto una facultad estante en sí misma, sino una "facultad parásita" de la sensación; como ha señalado D. Frede, "The Cognitive Role of Phantasia in Aristotle" en: Nussbaum, M. y A.O. Rorty (eds.), Essays on Aristotles De Anima, Oxford: Oxford University Press, 1992, pp. 297-311(traducción italiana: "La funzione conoscitiva de la phantasia in Aristotele", en: Cambiano, G. y L. Repici (eds.), Aristoteles e la conoscenza, Milán: Casa Editrice Ambrosiana/LED (Ed. Universitarie di Lettere Economia Diritto),1993, pp. 91-118, especialmente p. 94). Sin embargo, Frede defiende la pertenencia a la "fantasía" no solo de poderes discriminatorios, afines a los de la sensación, sino también de una función de "síntesis" de los datos perceptivos, análoga a la de la constitución de un "campo visivo", que es clara especialmente en su relación "con la razón práctica" (ibid., p. 104). Diversa es la opinión, por ejemplo, de H. Busche, "Hat Phantasie nach Aristoteles eine interpretierende Funktion in der Wahrnehmung?", en: Zeitschrift für Philosophie Forschung, LI (1997), pp. 565-589, que se añade al tratado más completo sobre la "fantasía" en Aristóteles publicado en los últimos años, a saber: Wedin, M.V., Mind and Imagination in Aristotle, New Haven/Londres: Yale University Press, 1988, especialmente. pp. 71-84. Para un más actualizado, aunque esencial, status quaestionis sobre la concepción de "fantasía" desarrollada por Aristóteles en el De anima, se puede consultar: Aristóteles, Lanima, editado por M. Zanatta con la colaboración de R. Grasso, Roma: Aracne, 2006, pp. 95-110, donde, sin embargo, no se toca el problema de la función y de la naturaleza de la "fantasía" en relación con la deliberación.
Aristóteles, De anima, III, 11, 434a5-8.
Cf
Cf
Sobre aspectos de la estructura de "cálculo" práctico, de los cuales se puede reconstruir una ascendencia vinculada al cálculo proporcional más difundido antes de Eudosio-Euclides, me permito recomendar: Cattanei, E., "Aristotele e i calcoli delluomo saggio", en: Migliori, M. (ed.), Non solo dialettica, non solo logica, Brescia: Morcelliana, Atti dei Convegni di Macerata 2002-2003 (en prensa).
Cf
Aristóteles, De anima, III, 11, 434a5-10.
Para una discusión de esta verdadera y auténtica tradición de la traducción, que se remonta a Filopón, ver Wedin, M.V., Mind and Imagination in Aristotle, p. 83, que la considera una traducción "not required" y "unnecessary".
Aristóteles, Lanima (1979), editado por G. Movia, Nápoles: Loffredo, 1991, p. 194. En la misma línea se encuentra M. Zanatta en: Lanima, p. 277. Cuando no se indique el nombre de los traductores, entiéndase que las traducciones son de quien escribe.
Cf
Este dato puede obtenerse fácilmente, más que de un reconocimiento lexicográfico, de: Heath, T., Mathematics in Aristotle, Oxford: Oxford University Press, 1949, capítulos IX, XVI.
Cf
Cf
Cf.
Cf
Ibid.
Ibid.
Cf
Ibid.
Cf
Ibid.
Ibid.
Cf. ibid.
En este sentido, la medición mediante unidades modeladas en las numéricas pertenece a aquellas a las que adecuadamente se ha denominado "técnicas para expresar el fenómeno de la invariancia", desarrolladas por la aritmética y la geometría "desde el antiguo pitagorismo", al tratar de "explicar cómo la transformación, el crecimiento y la disminución de las magnitudes podrían acompañar a la experiencia de la invariante y de lo idéntico", tratando de "definir relaciones homologantes, capaces de llevar lo diverso a lo idéntico" (Zellini, P., Gnomon.
Cf.
Cf
Cf
Lo "continuo" (toì sunexh=) a uno, dos, tres dimensiones constituye el objeto de la geometría plana y sólida según Aristóteles (cf. Cattanei, E., Enti matematici e metafisica, pp. 40-44). Sobre el carácter de continuidad –y de divisibilidad al infinito– de las magnitudes según Aristóteles, todas las referencias esenciales se encuentran en: Heath, T., A History of Greek Mathematics, 2 vols., Oxford: Oxford University Press, 1921; Nueva York: Dover,1981, pp. 342-344. Para un esudio más profundo sobre la concepción aristotélica de lo continuo desde el punto de vista de la investigación física, ver Wieland, W., Die aristotelische Physik (1961), Gotinga: Vandenhoeck & Ruprecht, 1970; traducción italiana de C. Gentili: La fisica di Aristotele, Bolonia: Il Mulino, 1993, pp. 351-399.
Cf
Cf
Véase Simplicio, In Arist. Phys., 454, 16ss Diels.
a)ntanai/resij, cf. Tópicos, VIII, 3, 158b29-35, junto a [ps.] Alessandro di Afrodisia, In Arist. Top. I, p. 545, especialmente ll. 15-19 Wallies. Se trata del "algoritmo euclideo", en torno al que gira la reconstrucción de las matemáticas de la Academia platónica propuesta por Fowler, D., The Mathematics of Platos Academy (1987), Oxford: Oxford University Press, 1990, y retomada, de manera más general, por Zellini, P., o.c., especialmente, pp. 162-207.
Al vínculo entre a)ntanai/resij e inconmensurabilidad está dedicada mucha literatura, señalada y discutida en: Cattanei, E., "Le matematiche al tempo di Platone e la loro riforma", en: Vegetti, M. (ed.), Platone, Repubblica, Libri VI-VII, Nápoles: Bibliopolis, 2003, pp. 473-539, especialmente pp. 500-509.
Además, Aristóteles (De anima, III, 11, 434a8), subraya que "es necesario" (a)na/gkh) que él proceda de ese modo para medir lo que se figura.
Este punto es adecuadamente puesto de relieve por Berti, E., "Differenza tra il metodo risolutivo degli aristotelici ela "resolutio" dei matematici", en: AA.VV., Aristotelismo veneto e scienza moderna, Pádua: Antenore, 1983, pp. 435-57, especialmente 442-445.
Sobre la relatividad entre fines y medios, basada en el hecho de que "a cada paso es posible redefinir el medio hallado, considerándolo como fin de un medio aun más particular", y sobre la consideración de los medios como "parte" del fin, cf. Natali, C., La sagezza di Aristotele, p. 173.
Cf.
Cf.
Cf
Ibid.
Ibid.
Ibid.
No solo las acciones poseen carácter de continuidad –y por lo tanto recaen en las "cosas cuyos extremos son uno" (Física, VI, 1, 231a22: sunexh= meìn wân taì e(/sxata, cf. Metafísica, I 1, 1052a19-21)–, sino que a partir de varias observaciones de Aristóteles –especialmente de De anima, III, 10, 433a15-17– surge que toda la dinámica interna de la acción humana es un continuo, definido por tres puntos: la cosa a la que tiende el deseo (o)/recij), la cual es "punto de partida del intelecto práctico" (a)rxh/ tou= praktikou= nou=), que alcanza un "extremo" (e(/sxaton), que a su vez es "punto de partida de la praxis" (a)rxh/ th=j pra/cewj). Véase que, si el intelecto práctico –como se está perfilando cada vez más claramente– alcanza desde su punto de partida a su extremo por "análisis" o descomposición, no procede en línea recta más allá del objeto del deseo, sino en sentido contrario a él, y justamente a lo largo del camino en sentido inverso, durante este "trayecto de retorno", su razonamiento se enlaza a la imaginación deliberativa.
Aristóteles, Ética Nicomáquea, III, 5, 1112b20-24 (traducción de C. Natali).
Para ese significado de dia/gramma es esencial referirse a Aristóteles, Sobre el cielo, 10, 279b34-280a10, donde él discute –en polémica con Jenócrates– sobre la "génesis" de las figuras, actuada en el contexto de un gra/fein (cf. ibid., 279b34), mediante una poi/hsij (cf. ibid., 280a3). Sobre el significado del pasaje en el marco de la discusión más amplia sobre la eternidad del cosmos, y sobre la referencia a Senócrates, cf. Aristóteles, Il cielo, edición de A. Jori, Milán: Bompiani, 2002, pp. 36-43, 201, 448.
Cf
Aristóteles, Metafísica, Q, 9, 1051a21-23: e)uri/sketai deì kaiì taì diagra/mmata e)nergei/#: diairou=ntej gaìr e)uri/skousin. Que en este pasaje Aristóteles tenga en mente no genéricamente "demostraciones geométricas", sino más exactamente "construcciones geométricas", es subrayado con claridad por D. Ross, en: Aristotles Metaphysics.
Cf
Cf
Ibid.
Ibid.
Cf
La construcción de Aristóteles –como Euclides, Elementos, I, 32– hace referencia a Elementos, I, 29 (una línea recta que corta dos rectas paralelas forma ángulos alternos iguales, el ángulo externo igual al ángulo interno opuesto, y los ángulos internos del mismo lado iguales a dos ángulos rectos), y a Elementos, I, 11 (dada una línea recta, se requiere trazar una línea perpendicular, que forme dos ángulos rectos en un punto de la línea dada).
Cf
Cf
Una fuente antigua –Pamfila en Diógenes Laercio– recuerda que Tales, luego de haber aprendido la geometría de los egipcios, "fue el primero en inscribir un triángulo rectángulo en una circunferencia y sacrificó un buey" (véase 11, A, 1 Diels-Kranz, II, 12-13); sin embargo, este "descubrimiento –como afirma Heath (Thirteen Books of Euclids "Elements", I, p. 317)– puede entenderse "en un sentido digamos que empírico (empirically, say)", y "por tanto es más natural suponer... que Tales lo haya probado (suponiendo que en verdad lo haya probado) prácticamente (practically), al igual que Euclides", en III, 31.
Aristóteles, Metafísica, Q, 9, 1051a31-32: poiou=ntej gignw/skousin.
La referencia al uso de la línea y del compás puede ser útil para comprender el pendant geométrico de la afirmación que Aristóteles hace a propósito de la prioridad "en la génesis" –o como oportunamnete traduce Natali, "en la realización"– del extremo alcanzado mediante análisis, citada en Ética Nicomáquea, III, 5, 1112b24 (cf. supra, n. 49): en el caso de la deliberación, esta prioridad es clara, en el sentido de que el extremo en el que ella se detiene es la acción que se elige y se realiza concretamente en lo inmediato; en el caso del análisis de los diagramas, la prioridad en el orden de la generación del extremo es que se detiene y puede ser entendida en relación al hecho de que la constucción gráfica de la figura –y por tanto su "génesis"– tiene su origen en el punto en donde se detiene la descomposición. Por ejemplo, en el caso ilustrado de la Figura 1, sea la génesis del triángulo ABC, sea de la paralela CE, parte del apoyo de la línea en el punto C, que es el extremo, en torno al cual se hacen evidentes las propiedades de los ángulos de ABC; o bien, en el caso ilustrado de la Figura 2, sea el semicírculo de partida, sea la perpendicular, son trazados a partir del D, el centro, sobre el que se coloca el compás y se apoya la línea, que es el punto en el que se descubre que todo triángulo inscrito en un semicircunferencia es rectángulo. Por lo demás –como en parte surge también del pasaje de Sobre el cielo, I, 10, 279b34-280a10, recordado anteriormente (cf. supra, n. 50)–, Aristóteles a menudo se pregunta sobre los significados de la ge/nesij de las magnitudes –que por sus contemporáneos es concebida, más o menos en sentido constructivo– indagando sobre los nexos de anterioridad y posterioridad, que ella tenía también entre las realidades no geométricas (cf. Cattanei, E., Enti matematici e metafisica, pp. 211-224). Además, en las Refutaciones sofísticas, 16, 175a27-30, hay una referencia a la recomposición por síntesis de los diagramas sometidos a análisis, lo que se puede interpretar como un proceso de "génesis" de las mismas figuras, a partir del último momento de su descomposición.
Sobre la geometría "visiva" –cuyo héroe puede ser considerado Hipócrates de Quíos, que propuso una demostración de la cuadratura de la lúnula dependiente de la observación de una figura (42 B 3 Diels-Kranz)–, y sobre la reforma a la cual la somete Platón, remito a: Cattanei, E., "Le matematiche al tempo di Platone e la loro riforma", pp. 473-539 , especialmente pp. 509-514, 534-539.
El ejemplo de la podi/aia, la "línea de un pie de largo", establecida como una unidad de medida, que, trazada en la arena, no carece de ancho, ni mide un pie de largo, y que por la tanto podría hacer falsas las demostraciones que se basan en ellas, es recurrente en Aristóteles; ver Analíticos primeros, I, 41, 49b33-37; Analíticos segundos, I, 10, 76b39-77a3; Metafísica, M, 3, 1078a19-21; N, 2, 1089a21-2, junto con: Cattanei, E., Enti matematici e metafisica, pp. 95-97; "Le matematiche al tempo di Platone e la loro riforma", pp. 488-493.
Aristóteles, Ética Nicomáquea, III, 5, 1112b22-23.
Cf
Cf
Cf.
Cf
Aristóteles, Ética Nicomáquea, VI, 9, 1142a26-27 (traducción de C. Natali).
Ibid.
Cf
Cf
El método de triangulación es practicado por la geometría griega, a la que se refieren Platón y Aristóteles, como método de comparación entre áreas, en las que se busca establecer relaciones de igualdad en el sentido explicado, por ejemplo, por D. Fowler (The Mathematics of Platos Academy, A new Recontruction (1987), Oxford: Oxford University Press, 1990, pp. 10-14), que de otro lado (cf. ibid., pp. 283-287), se muestra más bien escéptico con respecto a la herencia que las matemáticas griegas de la edad clásica habrían recibido de Egipto.
Cf
Cf
Cf
Aristóteles, Ética Nicomáquea, III, 5, 1112b7-9 (traducción de C. Natali).
Cf
Cf
Sobra la logistikh/ te/xnh, que es de fundamental importancia en Platón, remito a Cattanei, E., "Le matematiche al tempo di Platone e la loro riforma", pp. 500-509. Como disciplina matemática, ella desaparece en Aristóteles, quien además demuestra no ignorar sus términos, argumentos y procedimientos, incluso en la concepción de "cálculos prácticos", cf. Cattanei, E., "Aristotele e i calcoli delluomo saggio", § 3.
Cada sustracción del más pequeño al más grande, que se realiza durante la medición por sustracción repetida y recíproca (ver supra, n. 37), puede ser descrita mediante pares de números enteros –o lo/goi– dispuestos en una serie ordenada (ta/cij), que forman, en el caso de magnitudes conmensurables, una serie cerrada, que resulta en una unidad de medida; mientras que en el caso de magnitudes inconmensurables, la serie permanece abierta, aproximándose a un valor siempre más pequeño, que nunca es definido; cf. Cattanei, E., "Le matematiche al tempo di Platone e la loro riforma", pp. 505-507.
El tiempo que, como se sabe, es definido por Aristóteles como "número de movimiento según el antes y el después" (Física, IV, 11, 219b2), es una realidad en donde se encuentran lo continuo y lo discreto –lo continuo del movimiento, lo discreto del número que lo divide–, que, de lo contrario, quedan rigurosamente separados. Para una discusión del problema, que es muy antiguo, cf. Wieland, o.c., pp. 413-416; y, sobre todo, Sorabji, R., Time, Creation and the Continuum.
Aristóteles, De anima, III, 7, 431b7-9.
Cf
"Sobre el pasado no hay deliberación, si bien se delibera sobre el futuro y sobre lo que puede ser de otra manera", observa Aristóteles (ibid., 3, 1139b5-11, especialmente 7-9, en la traducción de C. Natali); pero, por otra parte, la experiencia es un requisito esencial para poder decidir bien, tanto así que difícilmente un joven puede ser sabio (cf. ibid., 9, 1142a11-16).
Aristóteles, La memoria y la reminiscencia, 2, 453a2-20, especialmente 10-12. Poco antes, en 452a3, Aristóteles ha elegido como ejemplo de anamnesis, en un contexto polémico en relación con el Menón de Platón, recurrir a la memoria por conocimientos matemáticos, que poseen una precisa ta/cij, tal como subraya R. Sorabji, Aristotle on Memory (1972), Londres: Duckworth, 2004, Chicago: University of Chicago Press, 2006, pp. 39-40, 102-103.
Aristóteles, La memoria y la reminiscencia, 2, 453a15-16, traducido por R. Laurenti en: Aristotele, Della generazione e della corruzione, Dellanima, Piccoli trattati di storia naturale, Roma/Bari: Laterza, 1983.
Cf
Cf
Sobre la relación entre deliberación y anamnesis, cf. Natali, C., La saggezza di Aristotele, pp. 145-149.
Cf
Cf
Tucídides, La Guerra del Peloponneso, I, 138, 3, especialmente 1-3 y 5, traducción de L. Canfora, Turín: Einaudi/Gallimard, 1996, p. 167.
Cf
Cf
En la Física, III, 4, 203a14-15 y en la Metafísica, N, 5, 1092b11-12, Aristóteles cita aplicaciones del gnōmōn a la aritmética de los números "figurados" de origen pitagórico, sobre los cuales véase Heath, T., A History of Greek Mathematics, pp. 76-77, 79. En Euclides, donde se señala (Elementos, II, def. 2) una extensión del significado geométrico del gnōmōn a partir de áreas cuadradas en paralelogramos (cf. Heath, T., The Thirteen Books of Euclids "Elements", I, pp. 370-372), se encuentra el llamado "Teorema del gnōmōn" (Elementos, I, 43). En efecto, se trata de una construcción que "se encuentra en el origen de una de las más importantes técnicas de las matemáticas griegas, a saber, la célebre aplicación de las áreas" (Zellini, P., o.c., p. 154). Consiste en aplicar en una recta dada, con un ángulo prefijado, la figura de un paralelogramo de área igual a la de un triángulo dado. Esta técnica lleva a cabo un principio de equivalencia de las áreas, en la medida en que permite construir (aplicándolo en una recta determinada) un paralelogramo o, en el caso más simple, un rectángulo de superficie igual a la de cualquier figura rectilínea dada (ya que una figura rectilínea puede ser resuelta en una composición de triángulos) (cf. ibid., p. 155).
Cf
Platón, Menón, 83d4-5, traducción de G. Reale, en: Platone, Menone, editado por G. Reale, Milán: 2000; y véase también sus notas de los comentarios ad loc.
Ibid.
Cf
Hornblower, S., A Commentary on Thucydides, 2 vols., Oxford: Clarendon Press, 1991, pp. 222-223, entiende la habilidad gnomónica de Temístocles como "actividades adivinatorias" de cara al futuro, conectadas con "new skills" –nacidas en el siglo V– "that claim to make inroads on the realm of the indeterminate", entre las cuales resalta la técnica de la que Aristóteles extrae más de un ejemplo para explicar la dinámica de la deliberación: la medicina.
Así Platón considera el ejercicio teórico de la logistikh/ –aplicada a la conmensurabilidad y a la inconmensurabilidad de las magnitudes– en República, VII, 526c6, sobre lo cual cf. Cattanei, E., "Le matematiche al tempo di Platone e la loro riforma", pp. 479, 506-509, 521-522.
Cf
Cf
Cf
Cf













