Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Areté
Print version ISSN 1016-913X
arete vol.23 no.2 Lima 2011
ARTÍCULOS
La crítica de Etchemendy al formalismo
Etchemendys critique to formalism
Matías Gariazzo
Universidad de la República, Uruguay
Resumen
John Etchemendy argumenta que, dado el fracaso del análisis tarskiano de la noción intuitiva de consecuencia lógica, no hay razones para considerar a la formalidad una condición necesaria para dicha relación. En el presente trabajo critico este argumento. Primeramente, busco mostrar que la crítica de Etchemendy al análisis tarskiano asume dos requisitos de éxito elucidatorio que no es razonable adoptar conjuntamente. En segundo lugar muestro que, rechazada la anterior asunción, dos argumentos a favor de la adecuación extensional de dicho análisis confieren apoyo al formalismo. Finalmente, menciono algunas conocidas consideraciones de índole pragmática en favor del formalismo.
Palabras clave: análisis, consecuencia lógica, formalismo, modelo, semántica.
Abstract
John Etchemendy claims that, given the failure of the Tarskian intuitive notion of logical consequence, there is no reason to consider formality as a necessary condition for this relationship. This paper critiques this argument. First, it seeks to show that Etchemendys critique to Tarskian analysis assumes two requisites of elucidatory success that cannot be held together reasonably. Secondly, it shows that, once the previous assumption is rejected, two arguments in favour of the extensional adequacy of the former argument actually support formalism. Finally, this paper reviews some well known pragmatic considerations in favour of formalism.
Key words: analysis, logical consequence, formalism, model, Semantics.
Tradicionalmente se ha considerado que una condición necesaria para que una oración sea una verdad lógica o una consecuencia lógica de un conjunto de oraciones es que tal verdad o relación sea, en un sentido a especificar, formal. A grandes rasgos, la condición de formalidad consiste en que una verdad lógica o un argumento lógicamente válido (esto es que exhibe la relación de consecuencia lógica entre sus premisas y conclusión) posea determinada forma lógica cuyas ejemplificaciones sean todas verdades o argumentos que preservan la verdad. Tales ejemplificaciones se obtendrían ya sea o sustituyendo ciertas expresiones de la oración o argumento por otras con distinto significado, pero igual categoría sintáctico-semántica, o reasignando valores semánticos (uniformemente y de modo apropiado a la categoría sintáctica y semántica de cada expresión) a estas expresiones. Aquellas expresiones que dejamos intactas al evaluar el estatus lógico de cualquier oración o argumento son las denominadas "constantes lógicas", las que constituirían una clase particular de expresiones por permitirnos abstraer la forma lógica de una oración o argumento. Consideremos un simple argumento considerado lógicamente válido:
-
Si Etchemendy trabaja en Stanford, entonces Etchemendy vive en Estados Unidos
-
Etchemendy trabaja en Stanford
Etchemendy vive en Estados Unidos
Resulta claro que al sustituir o reasignar valores uniformemente a las oraciones que arriba aparecen en letras cursivas, dejando intacta la expresión "Si , entonces", la preservación de la verdad de premisas a conclusión no se ve alterada. Así, usualmente se considera que la expresión "Si , entonces" es una expresión lógica y que las oraciones en cursivas son expresiones no lógicas.
Si sustituimos estas últimas oraciones por parámetros (esto es, expresiones que carecen de una interpretación previa) de oraciones y la anterior expresión por el conectivo veritativo funcional "→" (cuyo significado regimentaría el uso argumentativo dado a la anterior expresión del castellano), podemos obtener una representación de la forma lógica –a saber el Modus ponens– que se encontraría detrás de todos estos argumentos y explicaría su validez lógica:
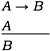
La correcta delimitación de los conjuntos de expresiones lógicas y de expresiones no lógicas resultaría así una cuestión crucial para la lógica. Por formalismo entenderemos aquí la posición que considera que la formalidad (la presencia de una forma lógica válida) es una condición necesaria para la verdad o consecuencia lógicas1.
John Etchemendy cuestiona esta posición tradicional. Según él, la formalidad no es ni una condición necesaria ni suficiente para que una oración sea una verdad lógica o un argumento sea lógicamente válido2. En el marco de su concepción –en la cual se acepta la noción de verdad o consecuencia en virtud del significado de ciertas expresiones– esta última tesis implica eliminar la distinción tradicional entre verdad o consecuencia lógica y verdad o consecuencia analítica. Estas últimas serían verdades o consecuencias en virtud del significado específico de cualesquiera expresiones (quizás todas las que figuran en una oración o argumento), no solo en virtud del significado específico de aquellas que tradicionalmente han sido consideradas constantes lógicas3. El argumento contra el formalismo que se desprende de la obra de Etchemendy se basa en su crítica a la tesis de que las definiciones de las nociones lógicas (verdad y consecuencia lógicas) propias de la teoría de modelos elucidan exitosamente las respectivas nociones intuitivas o preteóricas4.
Esquemáticamente, podemos reconstruir esta argumentación del siguiente modo: la razón fundamental para adoptar el formalismo es la corrección de las anteriores definiciones en tanto análisis conceptuales de las nociones preteóricas de verdad y consecuencia lógicas, pero, dado que dicho análisis es erróneo, no contamos con ninguna razón de peso para ser formalistas, y por ende para trazar una distinción entre verdades lógicas y analíticas o entre consecuencias lógicas y analíticas5. El propósito de este trabajo es mostrar que esta argumentación no es convincente.
En la primera parte presento a grandes rasgos la crítica de Etchemendy al análisis que supuestamente subyace a las definiciones de las nociones lógicas propias de la teoría de modelos, y busco mostrar cómo de esta crítica se desprendería un cuestionamiento al formalismo. En la segunda parte cuestiono la anterior argumentación de Etchemendy, aduciendo que ella se basa en un supuesto metodológico incorrecto consistente en exigir a un análisis la satisfacción conjunta de cierto par de requisitos. En la tercera parte muestro que, una vez abandonado este supuesto, dos conocidos argumentos a favor de la adecuación extensional de las definiciones de la teoría de modelos confieren apoyo al formalismo. Finalmente, en la cuarta y última parte considero una posible motivación de corte pragmático contra el formalismo que estaría implícita en la concepción de Etchemendy acerca del objeto de la lógica, concluyendo que carece de poder persuasivo debido a la existencia de consideraciones pragmáticas de mayor peso en favor del formalismo.
I
Como se indicó, Etchemendy cuestiona las definiciones de las nociones lógicas propias de la teoría de modelos en tanto análisis de las nociones intuitivas correspondientes (como se verá, para él tales definiciones pueden ser útiles para otros propósitos). El origen de estas definiciones, así como del análisis conceptual presuntamente subyacente a ellas, se encontraría en el artículo "On the Concept of Logical Consequence" escrito por Alfred Tarski en 1936. Según Etchemendy, es usual considerar que dichas definiciones logran, a diferencia de las caracterizaciones sintácticas, elucidar de forma matemáticamente precisa las nociones intuitivas de consecuencia y verdad lógica. Las caracterizaciones sintácticas no podrían elucidar estas nociones por el simple hecho de que están ligadas a un conjunto específico de reglas y a una clase particular de lenguajes; cualquier fórmula puede ser derivada de otras en algún cálculo, por lo que si queremos definir sintácticamente la relación de consecuencia lógica, debemos caracterizarla como derivabilidad en un cálculo correcto, lo que nos retrotrae directamente al concepto intuitivo que pretendíamos analizar6. Observaciones análogas pueden hacerse acerca de la noción de verdad lógica.
A continuación me centraré casi exclusivamente en la noción de consecuencia lógica debido a su particular importancia y al hecho de que las observaciones realizadas acerca de una de las nociones lógicas (verdad o consecuencia lógicas) pueden fácilmente extenderse, realizando modificaciones obvias, a la otra.
El concepto intuitivo o explicandum en el que se basa el análisis tarskiano coincide a grandes rasgos con las definiciones preteóricas de la noción de consecuencia lógica que encontramos en las introducciones de múltiples manuales de lógica. Ciertas notas que estas caracterizaciones atribuyen a la relación de consecuencia lógica darían cuenta de su especificidad, de aquello que permite diferenciarla de la mera consecuencia material7. Tarski caracteriza esta noción preteórica del siguiente modo: "Ciertas consideraciones de naturaleza intuitiva conformarán nuestro punto de partida. Considérese cualquier clase K de oraciones y una oración X que se sigue de las oraciones pertenecientes a esta clase. Desde un punto de vista intuitivo nunca puede suceder que la clase K consista solo de oraciones verdaderas y que la oración X sea falsa. Aun más, dado que estamos aquí interesados en el concepto de consecuencia lógica, i.e. de consecuencia formal, y así en una relación que se encuentra únicamente determinada por la forma de las oraciones involucradas en ella, la relación no puede ser influenciada por el conocimiento empírico, y en particular por el conocimiento acerca de los objetos referidos en la oración X o en las oraciones de la clase K. La relación de consecuencia no puede ser afectada por el reemplazo de las designaciones a los objetos referidos en estas oraciones por designaciones a cualesquiera otros objetos"8.
Este pasaje presenta tres rasgos comúnmente atribuidos de modo intuitivo a la relación de consecuencia lógica9: la preservación necesaria de la verdad de premisas a conclusión, a saber la imposibilidad de que las premisas sean verdaderas y la conclusión falsa; el carácter formal de esta relación, en la medida en que se encuentra únicamente determinada por la forma lógica de las oraciones involucradas (lo cual, según lo dicho al comienzo, presupone la existencia de cierta selección correcta de expresiones lógicas a partir de la cual abstraer la forma lógica de las oraciones); y, por último, la independencia de esta relación respecto al conocimiento empírico, rasgo que podemos denominar apriorismo. Como observa William H. Hanson10, debemos entender del siguiente modo esta última característica del explicandum: el conocimiento que podemos tener de los argumentos que exhiben la relación de consecuencia lógica lo podemos adquirir a priori, lo cual es consistente con que haya argumentos lógicamente válidos que no podemos conocer. Resulta natural vincular el primer y tercer rasgo: la validez a priori de un argumento puede ser una nota relevante para distinguir la necesidad propiamente lógica que este exhibe de otras clases de necesidad que podría exhibir, como la metafísica; a su vez, podríamos buscar dar cuenta del apriorismo a partir de tal transmisión lógicamente necesaria de la verdad11. Podríamos asimismo –siguiendo a Etchemendy– explicar estos dos rasgos a partir de una caracterización semántica intuitiva de la relación de consecuencia lógica, a saber aquella según la cual esta relación ocurre en virtud del significado específico de ciertas expresiones (aquellas consideradas lógicas) que intervienen en un argumento lógicamente válido. Finalmente, este conjunto de rasgos asociados a la relación de consecuencia lógica resulta indisociable de la siguiente característica epistémica: tal relación garantiza la preservación de la verdad de premisas a conclusión de modo independiente del efectivo valor de verdad tanto de las primeras como de la segunda.
No trataré aquí las complicadas cuestiones acerca de cómo entender exactamente el análisis tarskiano, y de si sus definiciones se corresponden con aquellas propias de la teoría de modelos12. A continuación simplemente explicaré a grandes rasgos las definiciones de la teoría de modelos y la mencionada crítica de Etchemendy a ellas.
En rigor, las definiciones de las nociones lógicas propias de la teoría de modelos se construyen para lenguajes formales particulares para los cuales se elabora una semántica formal particular13. Una semántica tal consiste en una clase de estructuras matemáticas denominadas modelos, y en una definición de la relación verdad en un modelo entre fórmulas y modelos (las fórmulas pueden o no ser verdaderas en un modelo). Dicho a grandes rasgos, los modelos asignan extensiones del tipo apropiado a las expresiones no lógicas de un lenguaje formal, asignaciones que permiten definir la relación verdad en un modelo. Como es sabido, para la teoría de modelos la caracterización general (no las definiciones construidas para lenguajes particulares) de la relación de consecuencia lógica es como sigue: una fórmula S es consecuencia lógica de un conjunto K de fórmulas si y solo si S es verdadera en todo modelo, en el cual todas las fórmulas del conjunto K son verdaderas. Puesto de otra forma, S es consecuencia lógica del conjunto K de fórmulas si y solo si el argumento conformado por el par ordenado <K, S> preserva la verdad (esto es, una de las fórmulas del conjunto K es falsa o S es verdadera) en todos los modelos. La caracterización general de verdad lógica propia de la teoría de modelos, por su parte, es la siguiente: una fórmula es lógicamente verdadera si y solo si es verdadera en todos los modelos14.
Las definiciones técnicas de las nociones lógicas construidas para lenguajes particulares constituyen así versiones rigurosas de la idea formalista preteórica de que un argumento es lógicamente válido si y solo si preserva la verdad bajo cualquier asignación intuitivamente realizada a las expresiones no lógicas, y una oración es lógicamente verdadera si y solo si es verdadera bajo cualquier asignación intuitivamente realizada a estas expresiones. Según estas caracterizaciones, la formalidad –entendida como verdad o su preservación bajo cualquier asignación– sería no solo una condición necesaria para que un argumento sea lógicamente válido o una fórmula lógicamente verdadera, sino también una suficiente. Así, según el análisis tarskiano, la satisfacción de la condición de formalidad por parte de un argumento o fórmula de algún modo garantiza la posesión de uno u otro de los rasgos ya sea modales, semánticos o epistémicos que intuitivamente consideramos notas esenciales de las verdades lógicas y de los argumentos lógicamente válidos.
Etchemendy observa que habría en principio dos modos distintos de entender la labor realizada por los modelos, modos que conducirían a delimitar de modo distinto la clase de todos los modelos al elaborar semánticas para ciertos lenguajes15. Es un lugar común considerar que la verdad de nuestras oraciones depende de dos parámetros: el lenguaje y el mundo. Consecuentemente, uno de los enfoques presupone un mundo o universo de discurso fijo, y entiende a los modelos como proveedores de distintos significados extensionales (construidos con los objetos del mundo actual) a las constantes no lógicas de un lenguaje, mientras el otro enfoque presupone un lenguaje cuyas expresiones no varían su significado de un modelo a otro, y concibe a los modelos como representaciones de las configuraciones posibles del mundo relevantes para los valores de verdad de las fórmulas de este lenguaje16. Así, mientras el primer enfoque explicaría el distinto valor de verdad de una fórmula en diferentes modelos a partir del distinto significado que ella adquiere en ellos, el segundo lo explicaría a partir de las distintas configuraciones posibles del mundo que representa cada modelo y en las que se evalúa la fórmula. Etchemendy denomina interpretacionales a las semánticas que suscriben el primer enfoque y representacionales a las que suscriben el segundo17.
Si bien Etchemendy considera que en ocasiones es posible entender como representacional una semántica de la teoría de modelos, observa que considerar las subsiguientes definiciones semánticas de las nociones lógicas como análisis de las correspondientes nociones intuitivas respecto al lenguaje que se está modelando supone entender dicha semántica como interpretacional18. La razón principal de esto es que un enfoque representacional utilizaría para delimitar la clase de todos los modelos (los cuales representarían todos los mundos lógicamente posibles relevantes) las propias nociones lógicas que buscamos analizar. Así, según Etchemendy, la semántica representacional no sirve para analizar las nociones lógicas, aunque sí podría ser utilizada con otros fines, como modelar las reglas semánticas de un lenguaje19.
Entendidas como el resultado último del análisis tarskiano, las semánticas propias de la teoría de modelos serían entonces interpretacionales. Buena parte de su virtud clarificadora residiría en que se habría operado una reducción de las nociones de verdad y consecuencia lógicas a las nociones –consideradas más claras y simples– de verdad y consecuencia material, dejando de lado nociones oscuras como las de necesidad lógica, apriorismo, preservación de la verdad en virtud del significado o garantía de tal preservación. Como se indicó, para una semántica de la teoría de modelos, una fórmula S es consecuencia lógica de un conjunto K de fórmulas si y solo si el argumento <K, S> preserva la verdad bajo todas las asignaciones a las constantes no lógicas avaladas por la teoría de modelos, y una fórmula es una verdad lógica si y solo si resulta verdadera en todas estas asignaciones. Si entendemos como interpretacional a una semántica formal, esto equivale a equiparar la validez lógica de un argumento a la mera preservación de la verdad de todas sus ejemplificaciones obtenidas mediante distintas interpretaciones, y la verdad lógica de una fórmula a la mera verdad de todas sus ejemplificaciones obtenidas del mismo modo.
La crítica de Etchemendy a las definiciones de la teoría de modelos admite ser explicada a grandes rasgos. El punto central es que si adoptamos una lectura interpretacional de estas definiciones, las verdades y consecuencias lógicas no tendrían por qué exhibir ninguno de los rasgos modales, semánticos o epistémicos señalados20. Consideremos la relación de consecuencia lógica. Para Etchemendy, la caracterización que la teoría de modelos ofrece de esta relación no brinda una garantía de que los argumentos considerados lógicamente válidos exhiban alguno de estos rasgos: el hecho de que un argumento preserve la verdad bajo todas sus interpretaciones puede simplemente deberse a ciertas características del universo de discurso. Según esto, la relación de consecuencia definida por una semántica de la teoría de modelos no ofrece una garantía de preservación de la verdad de premisas a conclusión que sea independiente del efectivo valor de verdad tanto de las primeras como de la segunda, ya que su interpretación actual es una de las interpretaciones a considerar21. Pero como hemos visto, el ofrecer una garantía tal es una característica central de la genuina relación de consecuencia lógica, y el análisis tarskiano pretendería capturarla. Lo único que garantizaría una definición de la teoría de modelos es que, dado un argumento con premisas verdaderas, si su conclusión es falsa el argumento es inválido, puesto que habría una interpretación de sus constantes no lógicas bajo la cual el argumento no preserva la verdad. Expresando el problema de un modo netamente epistémico: de acuerdo a una definición interpretacional de la relación de consecuencia lógica, dado un argumento válido (y una determinada interpretación de sus términos no lógicos) sería imposible inferir la verdad de la conclusión a partir del conocimiento de la verdad de las premisas, puesto que para determinar la validez del argumento habría que saber con antelación si su conclusión es materialmente verdadera22. Luego, se produciría una desconexión entre premisas y conclusión, en el sentido de que la relación de consecuencia lógica así definida no implica que las primeras, en caso de ser verdaderas, garanticen la verdad de la segunda. Esta situación, según Etchemendy, abre la posibilidad de que la configuración del universo de discurso influya en la delimitación de la extensión del concepto de consecuencia lógica23. Observaciones análogas pueden hacerse respecto a la noción de verdad lógica: la simple verdad de una fórmula bajo cualquier interpretación de sus constantes no lógicas no garantiza que esta posea alguno de los rasgos modales, epistémicos o semánticos intuitivamente atribuidos a las verdades lógicas. Según esto, una verdad lógica en la teoría de modelos no ofrece una garantía de ser verdadera que sea independiente de su efectivo valor de verdad, razón por la cual la definición permite la influencia de cuestiones ontológicas en la delimitación de la extensión del concepto considerado.
Ahora bien, el análisis tarskiano supone determinada selección de constantes lógicas, esto es, expresiones cuyo significado específico, podríamos decir, se mantiene fijo en el pasaje de un modelo a otro. Luego, resulta razonable considerar incompleto el análisis, en el sentido de que se encuentra necesitado de un análisis suplementario acerca de qué cuenta como una correcta selección de constantes lógicas. Este análisis debería explicar por qué determinada selección de expresiones lógicas permite a las definiciones de las nociones lógicas tener una correcta extensión, es decir sancionar como argumentos válidos y como verdades lógicas argumentos y fórmulas que posean los debidos rasgos epistémicos, semánticos o modales. Luego, se supone que la citada garantía distintiva de los argumentos intuitivamente válidos sería elucidada por una definición formal de consecuencia lógica suplementada con cierto análisis acerca de qué cuenta como una expresión de tipo lógico. Es fácil ver que si incluimos cualquier predicado o nombre en el conjunto de las constantes lógicas, la extensión dada a las nociones lógicas por una semántica interpretacional puede verse influenciada por cuestiones concernientes a la configuración particular del universo de discurso, a saber aquellas que tengan que ver con objetos que se encuentren en la extensión de un predicado o con el objeto denotado por un nombre24. A modo de ilustración, Etchemendy nos propone considerar argumentos como el siguiente, formulados en un lenguaje natural como el castellano:
-
Lincoln fue presidente de Estados Unidos
Lincoln fue un hombre
Si tomamos las expresiones "fue presidente de Estados Unidos" y "fue un hombre" como expresiones lógicas (manteniendo su interpretación intuitiva) y "Lincoln" como expresión no lógica, y consideramos al mundo real el universo a partir del cual construimos nuestros modelos, el argumento anterior sería, bajo una visión interpretacional de la semántica estándar, un argumento lógicamente válido. Por supuesto, si una mujer hubiera sido presidente de Estados Unidos tal argumento habría sido inválido, pero lo hubiera sido por cuestiones concernientes a los objetos del universo de discurso, no debido a que el análisis suplementado con esta selección de expresiones lógicas brinde alguna garantía intensional de corrección extensional25. Así, suele excluirse del conjunto de las constantes lógicas a los nombres y predicados (salvo el caso de la relación de identidad), y suele incluirse los conectivos veritativo funcionales, los cuantificadores universal y existencial, y el predicado de identidad, así como también todo término definible a partir de estas expresiones.
Etchemendy considera que no existe una selección de constantes lógicas que bloquee la influencia de la configuración del universo de discurso sobre la extensión de las propiedades lógicas definidas por una semántica interpretacional, y por ende tampoco un análisis exitoso de qué cuenta como una expresión de tipo lógico. La razón que presenta a favor de esta tesis es que, aun con la selección tradicional e incluso con otras más restrictivas, existen una serie de ejemplos de argumentos o fórmulas cuyo estatus lógico depende de cuestiones ontológicas, más precisamente de la cardinalidad (tamaño) del universo de discurso26. A modo de ilustración, considérese la fórmula P1a → P1b de un lenguaje formal de primer orden donde los conectivos veritativo funcionales son considerados constantes lógicas y los predicados y nombres expresiones no lógicas. Resulta claro que las ejemplificaciones interpretativas de esta fórmula no tienen por qué ser verdades lógicas, y que las ejemplificaciones interpretativas de los argumentos que tienen esta fórmula como conclusión no tienen por qué exhibir una garantía de preservación de la verdad independiente del efectivo valor de verdad de las fórmulas que lo componen. Sin embargo, al interpretar extensionalmente los predicados asignándoles conjuntos arbitrarios de objetos, en caso de que el universo conste de tan solo un objeto, esta fórmula sería verdadera bajo toda interpretación, por lo que sería declarada lógicamente verdadera, y los argumentos referidos serían por ende considerados lógicamente válidos. Según Etchemendy, si la fórmula anterior no es considerada una verdad lógica debido a que nuestro universo de discurso consta de más de un objeto, esto de todos modos revela una falla en el análisis tarskiano, ya que la correcta sanción se debería no a una garantía intensional de corrección extensional propia de sus definiciones, sino a la cardinalidad del universo. De hecho, según la teoría de modelos el argumento anterior es inválido, ya que una semántica formal construye los modelos para lenguajes de orden uno y superiores en base al universo de la teoría de conjuntos de Zermelo-Fraenkel, la cual acepta el axioma de infinitud. Este axioma garantiza la existencia de modelos con dominios con más de un objeto (de hecho, garantiza la existencia de modelos con dominios infinitos), en los cuales argumentos como el anterior no preservan la verdad. Pero, claro está, Etchemendy entiende que esta garantía no surge de un análisis provisto por las definiciones mismas de la semántica formal, sino de ciertos rasgos peculiares del universo de discurso27.
Ahora bien, según Etchemendy, si las definiciones de las nociones lógicas propias de la teoría de modelos, suplementadas con determinada caracterización o análisis de las constantes lógicas, ofreciera una garantía intensional de proporcionar una extensión correcta cuando una semántica interpretacional se construye para un lenguaje formal particular (en el sentido de no sobregenerar sancionando como lógicas y válidos verdades y argumentos que intuitivamente no lo son), contaríamos con una razón para considerar que existe una diferencia esencial entre expresiones lógicas y no lógicas que es crucial a la hora de definir el objeto de la lógica. Así, Etchemendy considera que su crítica socava la razón fundamental para considerar que existe una diferencia sustancial entre una y otra clase de expresiones. Por supuesto, podemos encontrar propiedades compartidas por las expresiones tradicionalmente consideradas constantes lógicas, como en principio podemos hacerlo con cualquier conjunto de expresiones; lo que la citada crítica socavaría es la idea de que estas propiedades contribuyen a definir, mediante un análisis interpretacional de las nociones lógicas, el objeto de estudio de la lógica.
A partir de estas observaciones, Etchemendy concluye que no contamos con razones para incluir la formalidad como una característica de nuestras nociones preformales de verdad y consecuencia lógica. Propone así que tomemos como objeto de la lógica toda verdad o consecuencia que exhiba los rasgos modales, epistémicos o semánticos comúnmente asociados entre sí y con las nociones lógicas. De acuerdo con esto, aquellas verdades y consecuencias tradicionalmente consideradas conceptualmente necesarias o analíticas, pero no lógicas, deberían considerarse lógicas28.
Una vez que tomamos en serio esta sugerencia podríamos afirmar no solo que una semántica propia de la teoría de modelos puede perfectamente sobregenerar, sino también que casi seguramente subgenerará (no sancionará como lógicas o válidos verdades y argumentos que intuitivamente lo son). En el marco de la concepción de Etchemendy es fácil ver cómo esto puede suceder: aquellas consecuencias y verdades en virtud del significado específico de expresiones que consideramos no lógicas (predicados y funciones) no serán consideradas verdades y consecuencias lógicas, ya que –tal como una semántica de la teoría de modelos delimita la clase de todos los modelos– siempre habrá alguna interpretación de estas expresiones bajo la cual las fórmulas en cuestión son falsas o los argumentos bajo consideración no preservan la verdad.
II
En esta sección buscaré mostrar que el cuestionamiento de Etchemendy a las definiciones de la teoría de modelos no es convincente. Como mencionamos al comienzo, el problema de la argumentación de Etchemendy contra el formalismo reside fundamentalmente en que se basa en cierto supuesto metodológico equivocado. Etchemendy cuestiona las mencionadas definiciones en tanto análisis conceptuales por no cumplir con cierto estándar de éxito elucidatorio. Más precisamente, asume dos requisitos controversiales para el éxito elucidatorio, el segundo de los cuales no sería cumplido por el análisis tarskiano29. Como se verá, es implausible que haya análisis formales30 propiamente dichos que satisfagan el segundo de los requisitos, y más implausible aun que haya o pueda haber análisis que satisfagan al mismo tiempo ambos requisitos.
El primero de estos requerimientos es el siguiente:
-
R1: Al construir el explicatum no debemos apelar de ningún modo a la noción que queremos analizar, so pena de circularidad.
Como se recordará, es aduciendo este requisito que Etchemendy descarta las definiciones semánticas representacionales como posibles análisis de las nociones lógicas. Etchemendy admite que esto no equivale a decir que una semántica representacional no puede proveer ninguna iluminación acerca de las propiedades lógicas de un lenguaje formal31. Una semántica tal nos proporcionaría un marco riguroso para caracterizar las reglas semánticas que gobiernan el uso de un lenguaje formal, mostrando cómo los valores de verdad de sus fórmulas dependen de las circunstancias no lingüísticas representadas por los modelos. Al delimitar la clase de modelos de una semántica representacional apelamos a la noción de necesidad que de algún modo pretendemos clarificar, pero esta noción oscura no es un componente del aparato técnico resultante. Ahora bien, es dudoso que esta distinción entre dos tipos de clarificación conceptual, una asociada a las definiciones resultantes de análisis conceptuales exitosos y la otra a otro tipo de definiciones o aparatos técnicos, sea significativa. Este requisito de Etchemendy se basa en cierta concepción tradicional del análisis conceptual, según la cual este debe ser rigurosamente reductivo, es decir, debe no presuponer de ningún modo las nociones que se pretenden clarificar. Esta concepción ha sido cuestionada por establecer un estándar de éxito analítico que no es razonable pedir en muchos contextos, y –como lo muestran las propias observaciones de Etchemendy acerca de la semántica representaional– por imponer un requisito que no es necesario cumplir para que haya algún tipo de clarificación conceptual32. De hecho, muchos filósofos interesados en el análisis tarskiano y en el análisis de las nociones lógicas en general rechazan tácitamente este criterio33. Así, aunque pueda trazarse la división mencionada entre dos clases de clarificaciones, no es claro qué tan significativa ella sea.
Como se habrá notado, el análisis tarskiano cumpliría con el primer requisito presentado (por más que su legitimidad sea dudosa) y Etchemendy lo entiende así. Es el segundo requisito el no satisfecho por el análisis tarskiano, y aquel en el que se basa la crítica de Etchemendy. Como sugiere Mario GómezTorrente34, este segundo requisito demanda que una oración que asevere que la extensión del explicatum se encuentra incluida en la del explicandum sea una verdad analítica o conceptualmente necesaria. Etchemendy correctamente señala que de acuerdo a las definiciones de verdad lógica propias de la teoría de modelos la siguiente oración, denominada por él principio de reducción, sería verdadera35:
-
PR: Si una fórmula universalmente cuantificada es verdadera, entonces todos sus casos son verdades lógicas.
Se sobreentiende aquí que las expresiones ligadas por cuantificadores universales son todas las expresiones no lógicas que figuran en la fórmula, y las expresiones no ligadas las constantes lógicas. Es claro que las definiciones de la teoría de modelos implican que PR es verdadero. Podemos asimismo formular el principio de reducción para el caso de los argumentos:
-
PR: Si todas las interpretaciones de las expresiones no lógicas de un argumento preservan la verdad, entonces el argumento es lógicamente válido.
Estos principios establecen la reducción, señalada en la primera sección, de las nociones de verdad y consecuencia lógica a las nociones –consideradas más claras y básicas– de verdad y consecuencia material36.
Como se indicó, Etchemendy correctamente señala que las definiciones de la teoría de modelos implican la verdad de estos principios. Pero él supone además que la tesis de que estas definiciones constituyen un análisis correcto de las nociones lógicas implica que estos principios son analíticamente verdaderos o conceptualmente necesarios. Una clara indicación de ello es su repetido reproche al análisis tarskiano por no ofrecer una garantía intensional de corrección extensional en su aplicación a lenguajes formales. Para Etchemendy, esta garantía debe provenir de las definiciones mismas de una semántica formal de modo independiente del universo con que se construyen los modelos, so pena de que el análisis fracase por depender de la influencia de cuestiones extra-lógicas para su corrección extensional. Resulta así difícil negar que si estas definiciones (el explicatum) ofrecieran garantías intensionales de que los conceptos que definen son extensionalmente adecuados a otros conceptos (el explicandum), entonces los principios PR y PR serían verdaderos analíticamente o por necesidad conceptual. ¿De qué otra manera podríamos entender el requerimiento de que el explicatum ofrezca una garantía intensional de corrección extensional? Así, el segundo requisito asumido por Etchemendy para el éxito elucidatorio es el siguiente:
-
R2: Las proposiciones que –como PR y PR– afirman que la extensión del explicatum se encuentra incluida en la del explicandum, deben ser verdaderas analíticamente o por necesidad conceptual.
Ahora bien, este segundo requisito es asimismo cuestionable: posiblemente no exista un análisis conceptual que, mereciendo ser así llamado, cumpla con él. El único caso de análisis exitoso que Etchemendy cita en su libro consiste en una definición que podemos afirmar que satisface este requisito, pero que no parece merecer el apelativo de análisis conceptual37. Etchemendy menciona determinada definición inductiva de N, el conjunto de números naturales, que sería un análisis correcto de la noción preteórica de número natural. La definición es la siguiente:
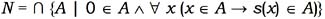
A pesar del lenguaje técnico en el que se encuentra formulada, esta definición tan solo dice que el conjunto de los números naturales es la intersección de todo conjunto (y por tanto el más pequeño) que satisface las siguientes dos condiciones: (i) contiene al cero y (ii) si contiene a un número x también contiene a s(x) = x + 1, esto es a su sucesor. Una vez que contamos con el método inductivo de definición, esta caracterización parece seguirse casi inmediatamente de la noción de número natural. Esto se debe no solo a que la definición no apela a grandes complejidades técnicas, sino también a que la noción preteórica de número natural no es una noción particularmente oscura o matemáticamente intratable. Esta última noción tiene una extensión precisa y necesaria (basta entender el concepto para conocer su extensión), y la definición inductiva se construye sobre ella. Consecuentemente, si bien podríamos decir en este caso que una oración que asevera que la extensión del concepto definido inductivamente está incluida en la extensión del concepto preteórico de número natural es una verdad analítica o conceptualmente necesaria, no parece que este sea un caso de análisis conceptual propiamente dicho. Por otra parte, nótese que si consideramos la definición de número natural de la teoría de conjuntos donde se asocia el cero con el conjunto vacío, el uno con el conjunto que contiene al conjunto vacío como único elemento, y así sucesivamente, ya no resulta claro que la oración correspondiente acerca de su adecuación extensional sea una verdad analítica o necesaria conceptualmente.
Pero –y esto es lo que ante todo quiero señalar– nótese además que resulta en extremo implausible, sino imposible, que pueda haber un análisis formal propiamente dicho que satisfaga los dos requisitos simultáneamente. R1 exige que el análisis sea reductivo, esto es que no presuponga de ningún modo en sus definiciones técnicas el concepto preteórico a analizar, mientras que R2 exige que haya una relación intensional entre el explicandum y el explicatum que haga a las oraciones referidas acerca de la adecuación extensional del primero verdades analíticas o conceptualmente necesarias. Es difícil ver cómo un análisis formal propiamente dicho podría ser al mismo tiempo no reductivo y garantizar que principios como PR y PR sean verdades de tal índole: presumiblemente el precio a pagar por satisfacer R1 es no satisfacer R2 y viceversa. El supuesto metodológico de que un análisis formal debe satisfacer conjuntamente estos requisitos no es entonces razonable38. Según esto, la crítica de Etchemendy resulta irrelevante, en tanto consiste en cuestionar el análisis tarskiano por no satisfacer simultáneamente dos requisitos que no es posible satisfacer en forma conjunta.
Etchemendy podría replicar que de todos modos podemos concluir que el análisis tarskiano, al igual que cualquier otro análisis, al no poder satisfacer conjuntamente estos requisitos (probablemente imposibles de satisfacer simultáneamente), no ofrece un fundamento último para el formalismo. Pero, dada la incorrección del supuesto metodológico de que un análisis formal debe conjuntamente satisfacer estos requisitos, no tiene sentido buscar en semejante análisis el fundamento último para definir el objeto de estudio de una disciplina. Luego, no podemos extraer consecuencias de peso a partir del hecho de que un análisis particular fracasa en satisfacer estos requerimientos y en proporcionar tal fundamento.
Por supuesto, siempre es posible reservar la expresión "análisis" para algo que satisfaga los dos requisitos de Etchemendy o tan solo el segundo. Pero al hacer esto volvemos a los análisis formales tareas intelectuales o bien imposibles o bien de poca relevancia filosófica. Como vimos, parece imposible que pueda haber análisis formales propiamente dichos que satisfagan simultáneamente los anteriores requisitos. Y, por otra parte, si junto a la aceptación de estos requisitos consideramos como análisis conceptual a cualquier definición que introduzca una dosis mínima de rigor (como en el caso de la definición inductiva de número natural), no parece que los análisis exitosos merezcan mayor atención filosófica. Quizás debido al carácter no razonable de estos requisitos a veces impuestos a un análisis conceptual, cierto número de autores han simplemente negado que una buena caracterización de una noción intuitiva deba consistir en un análisis conceptual39.
Ahora bien, como se mostrará en la siguiente sección, una vez admitida la incorrección del mencionado supuesto metodológico, puede argüirse que en caso de que las definiciones de la teoría de modelos sean correctas a la luz de criterios razonables, contamos con una razón –aunque no con un fundamento último– para adoptar el formalismo. Por otra parte, como se sugerirá en la cuarta y última sección, la tesis avanzada por Etchemendy de que la corrección del análisis tarskiano constituye la razón fundamental, o incluso la única razón a favor del formalismo, es falsa.
III
Como se vio en la primera sección, las caracterizaciones preteóricas de las nociones lógicas a veces incluyen la analiticidad como un rasgo central de estas nociones, y Etchemendy prioriza estas caracterizaciones informales sobre otras. La analiticidad es una propiedad que las fórmulas o argumentos poseen tan solo en virtud del significado de (al menos) algunas de sus expresiones, esto es, de modo independiente a la configuración del universo de discurso. La admisión conjunta de esta caracterización informal de las nociones lógicas y de R2 conduciría a Etchemendy a sostener que no podemos considerar que el universo de la teoría de conjuntos de Zermelo-Fraenkel se encuentre presupuesto por el análisis subyacente a las definiciones de la teoría de modelos.
Así, propone diversos contraejemplos al análisis donde el universo de discurso es el mundo empírico (recuérdese el argumento acerca de Lincoln). Ahora bien, en tanto rechacemos R2, nada nos impide evaluar las definiciones de la teoría de modelos –y por ende el análisis tarskiano presuntamente subyacente a ellas– tomando en cuenta el universo de la teoría de conjuntos a la que dicha teoría aplica estas definiciones; podríamos hacer esto incluso aceptando las caracterizaciones preteóricas recién mencionadas. Según esto, la evaluación de las definiciones consideradas puede ser extensional. A continuación presentaré dos argumentos en favor de la adecuación extensional de las definiciones de las propiedades lógicas en el marco de la teoría de modelos. Esta adecuación confiere apoyo al formalismo, en tanto muestra la viabilidad de un importante proyecto semántico que lo asume. Cabe indicar que el segundo argumento solo muestra la adecuación extensional de las definiciones aplicadas a lenguajes de primer orden, y que no existen argumentos definitivos en favor de su adecuación o inadecuación extensional respecto a lenguajes de órdenes superiores40.
Vann McGee41 presenta un argumento que mostraría que PR y PR, aunque no sean analítica o conceptualmente verdaderos, sí lo son por necesidad metafísica. Su idea central es que los modelos construidos a partir del universo de objetos matemáticos de la teoría de conjuntos de Zermelo-Fraenkel en cierto sentido modelan todos lo modelos posibles, incluidos aquellos construidos con elementos empíricos reales o posibles. Un modelo de una semántica de la teoría de modelos modela algún otro modelo si es isomorfo a él. Dado el hecho de que una fórmula de un lenguaje formal es verdadera en un modelo si y solo si es verdadera en todo modelo isomorfo a él, la extensión de las definiciones de una semántica de la teoría de modelos incluiría solo fórmulas y argumentos con el rasgo modal (preteórico) apropiado (el cual, como se vio en la primera sección, suele asociarse a otros rasgos preteóricos). Los modelos de una semántica tal son normalmente concebidos como necesariamente existentes, dada su condición de entidades puramente matemáticas. Dado que para cualquier modelo habría un modelo puramente matemático, construido a partir del universo de la teoría de conjuntos de Zermelo-Fraenkel, que resulta isomorfo a él, McGee concluye que si es posible que haya un modelo en que determinada fórmula sea falsa o determinado argumento no preserve la verdad, entonces efectivamente existe un modelo tal.
Un problema que puede señalarse sobre este argumento es que la colección de todos los modelos intuitivamente posibles, esto es aquella colección responsable de recoger el rasgo modal preteórico, incluye modelos con dominios demasiado grandes para ser conjuntos, y que por ende no resultan isomorfos a ningún modelo propio de una semántica de la teoría de modelos. Pero no es claro que estos modelos provean asignaciones legítimas (por más que intuitivamente lo parezcan), ya que, como es sabido, las colecciones de mayor cardinalidad que los conjuntos conducen a contradicciones. De todos modos, existe un argumento a favor de la adecuación extensional de las definiciones de la teoría de modelos aplicadas a lenguajes de primer orden que no es sensible a la anterior dificultad.
El argumento referido fue introducido por primera vez por Georg Kreisel42. Kreisel considera que la noción intuitiva de verdad o consecuencia lógica consiste en la noción formalista de verdad o su preservación bajo toda asignación intuitiva realizada a las expresiones no lógicas. Asimismo, considera que la noción preformal de asignación puede caracterizarse como la asignación a los lenguajes de modelos cuyos dominios pueden ser clases actuales, y no solo conjuntos actuales. Kreisel muestra que esta noción preformal de verdad y consecuencia lógica es coextensional con las nociones correspondientes de la teoría de modelos en su aplicación a lenguajes de primer orden, asumiendo todas las técnicas utilizadas por las semánticas de dicha teoría (estas incluyen el uso de la teoría de conjuntos ya mencionada, la selección tradicional de constantes lógicas y la variación de dominio de modelo a modelo).
Gómez-Torrente43 generaliza este argumento mostrando que lo mismo puede ser demostrado considerando como intuitiva la asignación de modelos cuyos dominios son clases o conjuntos posibles. Esto permite recoger el rasgo modal preteórico señalado en el párrafo anterior.
Consideremos la relación de consecuencia lógica44. Es claro que, tomando cualquiera de estas caracterizaciones de la noción preteórica de consecuencia lógica, si un argumento no es lógicamente válido según la teoría de modelos, entonces tampoco lo será intuitivamente. Por lo tanto, podemos afirmar lo siguiente:
(i) Para todo argumento <K, S> (<K, S> es VPT → <K, S> es VTM).
"<K, S>" representa aquí cualquier argumento concebido como un par ordenado, donde K es el conjunto de premisas y S la conclusión. Por su parte "VPT" significa lo mismo que "válido preteóricamente" y "VTM" lo mismo que "válido para la teoría de modelos".
La segunda observación de la que depende el argumento es que podemos convencernos de que un sistema deductivo es extensionalmente adecuado en el sentido de no sobregenerar (esto es permitir la derivación a partir de un conjunto de premisas de fórmulas que intuitivamente no son consecuencias lógicas de ese conjunto). Para lograr esto basta cerciorarse de que los axiomas del sistema son verdades lógicas preteóricas, y de que las reglas de inferencia son intuitivamente válidas. Así, supóngase que contamos con un cálculo deductivo estándar C correcto (en el sentido de no sobregenerar) para un lenguaje de primer orden. Podemos entonces aseverar lo siguiente:
(ii) Para todo argumento <K, S> (S es derivable en C a partir de K → <K, S> es VPT).
Para estos sistemas deductivos contamos con el célebre teorema de compleción, el cual prueba lo siguiente:
(iii) Para todo argumento <K, S> (<K, S> es VTM → S es derivable en C a partir de K).
A partir de las aseveraciones (i), (ii), y (iii) concluimos, aplicando transitividad, que las nociones VPT, VTM y derivable en C son coextensionales:
(iv) Para todo argumento <K, S> (<K, S> es VPT ↔ <K, S> es VTM ↔ S es derivable en C a partir de K).
Por supuesto, este argumento funciona en tanto aceptemos la idea formalista de que un argumento es válido si preserva la verdad bajo toda asignación extensional intuitiva realizada a sus expresiones no lógicas. Pero, según se vio, no hemos visto ninguna razón de peso para no aceptar esta concepción. Además, si aceptamos la caracterización preteórica de consecuencia lógica que apela a la asignación a los lenguajes de modelos no solo actuales, sino también posibles, no puede objetarse que el rasgo modal (y posiblemente los otros rasgos a él asociados) no resulte indirectamente recogido por las definiciones de la teoría de modelos. No obstante, aunque no aceptemos ninguna de estas nociones lógicas preteóricas, aún podemos –como muestra Etchemendy45– utilizar las observaciones de Kreisel para mostrar que una semántica de la teoría de modelos no sobregenera en su aplicación a lenguajes de primer orden. Si aceptáramos una noción preteórica de consecuencia lógica no formalista no podríamos aceptar (i), pero podríamos seguir aceptando (ii) y por supuesto también (iii). Ahora bien, a partir de (ii) y (iii) podemos concluir lo siguiente:
(v) Para todo argumento <K, S> (<K, S> es VTM → <K, S> es VPT).
Aquí "VPT" expresa cualquier noción preteórica (razonable) de consecuencia lógica.
IV
Tarski esperaba encontrar una caracterización en términos matemáticos de la noción de constante lógica que tuviera como extensión las expresiones comúnmente así consideradas, con el fin de prescindir de una noción intuitiva de expresión lógica en su análisis formal de las nociones lógicas. Muchos análisis o caracterizaciones de esta clase se han ensayado (el propio Tarski adelantó una propuesta), pero hay razones para pensar que ninguno de ellos es satisfactorio46. Consecuentemente, cierto número de filósofos han considerado que una caracterización correcta del conjunto de las constantes lógicas solo puede darse en términos pragmáticos47. Como observa Gómez Torrente48, dado que probablemente las expresiones lógicas han sido seleccionadas mediante la aplicación de complejos principios pragmáticos, no es razonable esperar que puedan darse condiciones necesarias y suficientes en términos matemáticos o semánticos para las constantes lógicas. Siendo así, la ausencia de una caracterización o análisis formal de la noción de constante lógica no invalida el análisis tarskiano. Sea como fuere, Etchemendy considera que el supuesto fracaso de este análisis justifica el abandono del formalismo. Aparentemente él entiende que, una vez admitido tal fracaso, contamos con cierta motivación de corte pragmático para abandonar toda distinción sustancial entre expresiones lógicas y no lógicas. Para terminar, quisiera sugerir que contrariamente a lo que Etchemendy piensa, existen mejores razones de tipo pragmático para aceptar el formalismo, a saber aquellas que se desprenden de los principios pragmáticos que ciertos autores han propuesto para seleccionar las constantes lógicas49.
Etchemendy considera que, dado el (supuesto) fracaso del análisis tarskiano, contamos con una motivación para ampliar el objeto de la lógica al estudio de cualquier inferencia o verdad que exhiba los rasgos modales, semánticos o epistémicos señalados en la primera sección, incluidas aquellas inferencias o verdades que involucran sistemas de representación como los diagramas o las bases de datos: al ampliar el objeto de la lógica de este modo, daríamos una visión unificada de un conjunto amplio de relaciones inferenciales y verdades para las cuales no contaríamos con razones para tratarlas por separado50.
Pero resulta que sí contamos con tales razones, por lo que este último supuesto de Etchemendy es falso. Tradicionalmente (posiblemente desde Aristóteles) se ha considerado que la utilidad de la lógica reside principalmente en que estudia aquellos principios del razonamiento aplicables a una gran diversidad de ámbitos, permitiendo de este modo ya sea la comparación entre teorías científicas o la clarificación de confusiones presentes en diversas esferas de la actividad intelectual51. De acuerdo con esto, la selección de las constantes lógicas está guiada por principios como el de generalidad, el cual exige que los términos lógicos sean expresiones utilizadas en una gran diversidad de esferas, o el de utilidad, el cual requiere que las constantes lógicas sean expresiones relevantes para el estudio del razonamiento en general y sus confusiones52. Dado que este modo de delimitar el objeto de la lógica al mismo tiempo cuenta con una larga tradición y no presenta ninguna inconsistencia interna, la propuesta de Etchemendy tiene la carga de la prueba. Y dado que Etchemendy no ofrece razones convincentes en favor de su propuesta, ella resulta en última instancia gratuita. En otras palabras, la existencia de relaciones inferenciales y verdades que no siendo formales exhiben los rasgos modales, semánticos o epistémicos asociados a las nociones lógicas no constituye una razón suficiente para cambiar el objeto de estudio de la lógica, en la medida en que este se encuentra razonablemente bien definido53.
-
1 La posición aquí caracterizada como formalismo es una concepción muy general acerca de la lógica. Existen muchos modos específicos de entender en qué consiste exactamente la forma lógica de una oración y, en consecuencia, diversas maneras particulares de entender la tesis de que la lógica es una disciplina formal (cf. McFarlane, J.G., What does it mean to say that logic is formal?, Pittsburgh: University of Pittsburgh, 2000, pp. 50-78).
-
2 Esto, claro está, no supone que Etchemendy no considere que la abstracción de formas oracionales o argumentales no sea una estrategia útil para estudiar simultáneamente innumerables verdades lógicas o argumentos válidos (cf. Etchemendy, J., "The Doctrine of Logic as Form", en: Linguistics and Philosophy, VI (1983), pp. 319-334, pp. 320-322).
-
3 Comúnmente se considera que una vez aceptada la noción de verdad en virtud del significado, las verdades lógicas serían un subconjunto de las analíticas. Un ejemplo conocido de una verdad que sería tan solo analítica es "todos los solteros son hombres no casados", mientras que, por otra parte, "Etchemendy es un hombre casado" sería una consecuencia tan solo analítica de "Etchemendy no es soltero". El carácter analítico de dicha verdad y consecuencia se debería a la relación entre los significados de "soltero" y "hombre casado".
-
4 Por las nociones lógicas intuitivas o preteóricas entendemos aquí aquellas nociones previas a las definiciones técnicas y que guían su elaboración. Las nociones lógicas intuitivas serían, por tanto, nociones surgidas en el desempeño de la disciplina lógica. Para identificar el explicandum –esto es la noción preteórica a analizar mediante una más precisa, a saber el explicatum– podríamos en principio, como sugiere William H. Hanson, apelar a las caracterizaciones que de estas nociones realizan los manuales de lógica para introducir a la disciplina a los no iniciados (cf. Hanson, W.H., "The Concept of Logical Consequence", en: The Philosophical Review, CVI (1997), pp. 365-409, p. 366).
5 Cf. Etchemendy, J., "The Doctrine of Logic as Form", pp. 319-334.
6 Cf. Etchemendy, J., The Concept of Logical Consequence, Cambridge, Mass.: Harvard University Press, 1990, pp. 2-3.
7 Esta expresión es usada por Tarski para referirse a la relación entre premisas y conclusión presente en argumentos que meramente preservan la verdad (tienen o al menos una premisa falsa o la conclusión verdadera) (cf. Tarski, A., "On the Concept of Logical Consequence", en: Logic, Semantics, Metamathematics, segunda edición, editado por J. Corcoran y traducido por J.H. Woodger, Indianápolis: Hackett, 1983, pp. 409-420, pp. 414-415).
8 Ibid. La traducción al castellano de la versión en inglés es nuestra. El pasaje en su versión en inglés es como sigue: "Certain considerations of an intuitive nature will form our starting-point.
9 Con adaptaciones triviales, estos tres rasgos también caracterizan la noción intuitiva de verdad lógica.
10 Cf. Hanson, W.H., o.c., pp. 377-378.
11 Existen autores que no entienden de este modo el vínculo entre estas características de la relación de consecuencia lógica. Por ejemplo, Hanson entiende que existe una única noción primitiva de necesidad (cf. ibid., pp. 380-390).
12 La teoría de modelos fue de hecho elaborada en los años cincuenta, en un período muy posterior al mencionado artículo de Tarski (cf. Tarski, A. et al., Undecidable Theories, Ámsterdam: North-Holland, 1953). Etchemendy, sin embargo, considera que en tanto haya un análisis de las nociones lógicas intuitivas subyacente en la teoría de modelos, este análisis será encontrado en el artículo de Tarski de 1936. Esta es una tesis filosófica que se desprende del hecho de que este autor considera que, como se verá, solo una semántica interpretacional como la que se desprende del mencionado artículo puede en principio proveer un análisis de las nociones lógicas. La concepción de Etchemendy también incluye cierta visión histórica controversial, según la cual las semánticas propias de la teoría de modelos habrían sido entendidas como interpretacionales, no como representacionales. No me centraré aquí en los aspectos históricos de la concepción de Etchemendy.
13 Propiamente hablando, entonces, no habría una definición de verdad y consecuencia lógica propia de la teoría de modelos, sino muchas definiciones relativas al lenguaje formal para el que se elabora una semántica formal. De todos modos, hay un método general para construir dichas definiciones.
14 Asimismo, es posible definir esta noción en base a la noción general de consecuencia lógica propia de la teoría de modelos: una fórmula S es lógicamente verdadera si y solo si es consecuencia lógica, según la teoría de modelos, de cualquier conjunto de fórmulas del lenguaje en cuestión (incluido el conjunto vacío).
15 Cf. Etchemendy, J., The Concept of Logical Consequence, pp. 12-26, 51-64.
16 Si la clase de todos los modelos proporcionada por una semántica representacional logra representar todas las posibles configuraciones del mundo relevantes para el valor de verdad de las fórmulas de un lenguaje, entonces resulta claro que las fórmulas que son verdaderas en todo modelo son todas las verdades necesarias, y los argumentos que preservan la verdad en todo modelo son todos aquellos que lo hacen necesariamente. En su ensayo de 1999, Etchemendy presenta un modo alternativo de entender el enfoque representacional, según el cual una semántica que se adhiera a él no busca modelar todas las configuraciones del mundo relevantes para los valores de verdad de las fórmulas de un lenguaje (cf. Etchemendy, J., Reflections on Consequence, Palo Alto: Stanford University Press, 1999, pp. 24-34).
17 Etchemendy muestra que, si bien algunas semánticas pueden entenderse ya sea como interpretacionales o como representacionales, esta situación es fortuita. Los criterios para delimitar la clase de todos los modelos en la construcción de una u otra clase de semántica difieren radicalmente, por lo que muchas posibles semánticas no admitirían ser entendidas tanto de un modo como de otro (cf. Etchemendy, J., The Concept of Logical Consequence, pp. 57-64; Reflections on Consequence, pp. 24-34).
18 El análisis de Tarski de 1936, por su parte, se inscribe claramente dentro del enfoque interpretacional. Esto resulta claro a la luz de la observación realizada por Tarski de que en el caso extremo en el que se consideren constantes lógicas todas las expresiones de un lenguaje, la noción de verdad lógica coincidiría con la de verdad material, y la noción de validez lógica de un argumento con la de mera preservación de la verdad de premisas a conclusión, lo que, en términos de Tarski, supondría la coincidencia del concepto de consecuencia lógica con el de consecuencia material (cf. Tarski, A., o.c., p. 419).
19 Cf. Etchemendy, J., The Concept of Logical Consequence, pp. 25-26; Reflections on Consequence, p. 33.
20 Cf. Etchemendy, J., The Concept of Logical Consequence, pp. 95-106; Reflections on Consequence, pp. 3-9.
21 En el caso en que esta interpretación sea intuitiva, se supone que una semántica formal provee un modelo que modela dicha interpretación.
22 Esto se tornaría evidente si todas las expresiones que ocurren en un argumento fueran constantes lógicas, ya que en tal caso su mera preservación de la verdad equivaldría a su validez lógica.
23 Por supuesto, habría formas argumentales –como el Modus ponens–, intuitiva y legítimamente válidas, que proporcionan una garantía de que todas sus ejemplificaciones preservan la verdad, que es independiente del valor de verdad de las fórmulas involucradas. El punto de Etchemendy es que tal garantía no puede provenir de la mera preservación de la verdad bajo toda interpretación asignada a un argumento con esta forma; tal preservación sería un efecto de la validez de la forma argumental en cuestión, no su causa (cf. ibid., p. 9).
24 Cf. Etchemendy, J., The Concept of Logical Consequence, pp. 107-135.
25 Las semánticas de la teoría de modelos adoptan un universo de objetos matemáticos (con los cuales construye los dominios de cada modelo), no de objetos empíricos. Las cuestiones concernientes a estos objetos matemáticos serían, en tanto ontológicas, sustantivas y no lógicas, aunque pueda ser razonable no considerarlas contingentes.
26 Cf. Etchemendy, J., ibid., pp. 111-135; Reflections on Consequence, pp. 10-20.
27 Etchemendy también observa que, dada la selección usual de constantes lógicas, si las semánticas de la teoría de modelos no variaran el dominio de cuantificación de modelo a modelo, tomando distintas subcolecciones del universo de la teoría de conjuntos de Zermelo-Fraenkel, declararían lógicamente válidas las siguientes fórmulas de un lenguaje de primer orden (las cuales aseveran que el universo tiene al menos cierto número i de elementos):
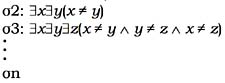
La razón de esto es que tales fórmulas –al igual que sus respectivas negaciones, a las cuales a continuación me referiré– solo constan de expresiones consideradas lógicas, por lo que su simple verdad equivale a su verdad lógica (la fórmula es trivialmente verdadera bajo toda interpretación). Por otra parte, dada la disponibilidad de modelos con dominios infinitos asegurada por el axioma de infinitud propio de la teoría de conjuntos en que se basa la teoría de modelos, las siguientes fórmulas (las cuales aseveran que el universo contiene menos de cierto número i de elementos) no son declaradas lógicamente válidas, lo cual es correcto:
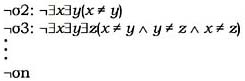
Pero, observa Etchemendy, una semántica formal no sobregenera en este caso (al igual que en el caso presentado en el texto principal) gracias no a la corrección de sus definiciones de las propiedades lógicas, sino al axioma de infinitud, el cual constituye una asunción extra-lógica acerca del universo de discurso. Podríamos considerar el predicado de igualdad una expresión no lógica, pero como muestra el ejemplo del texto principal, el problema de todos modos se presenta con otras fórmulas (cf. Etchemendy, J., The Concept of Logical Consequence, pp. 111-116).
28 El siguiente pasaje, donde Etchemendy trata una inferencia tradicionalmente considerada lógica y otra tradicionalmente considerada analítica, apoya claramente lo dicho en este párrafo: "Of course, most philosophers have been raised, under the influence of Quine, to say that the former inference is an instance of logical consequence, while the latter is something quite different: analytic consequence or something of the sort. But the idea that the justification underlying the first inference is different in kind from the second is supported by nothing more than the fact that the reductive account of consequence can be made to work in the first case but not in the second. Given the flaw in the reductive account, this is hardly a persuasive consideration" (Etchemendy, J., Reflections on Consequence, p.18). Asimismo, el siguiente pasaje donde Etchemendy se refiere a la teoría sintáctica (aquella que propondría sistemas deductivos como análisis de las nociones lógicas) y a la teoría tarskiana, muestra el mismo punto: "I have argued that there is no reason to think that either of these theories is a correct account of the logical properties, of the intuitive logical properties we recognize among sentences of our native language. Consequently, I see no reason, no reason stemming from the philosophy of logic, to adopt the doctrine of logic as form". A continuación, Etchemendy sugiere que no habría otro tipo de razones para aceptar el formalismo (Etchemendy, J., "The Doctrine of Logic as Form", pp. 333-334).
29 Por supuesto, hay criterios de éxito elucidatorio que serían aceptados por cualquiera, como que el explicatum sea más claro y riguroso que el explicandum o que exista cierta adecuación extensional del primero respecto del segundo.
30 Por análisis formal entiendo aquí todo análisis conceptual cuyo explicatum sea un concepto técnico o matemático.
31 Cf. Etchemendy, J., The Concept of Logical Consequence, pp. 25-26; Reflections on Consequence, pp. 33-34.
32 Cf. Wright, C., "Truth: A Traditional Debate Reviewed", en: Blackburn, S. y K. Simmons (eds.), Truth, Oxford: Oxford University Press, 1999, pp. 203-238.
33 Cf. Hanson, W.H., o.c., pp. 380-390; Shapiro, S., "Logical Consequence: Models and Modality", en: Schirn, M. (ed.), The Philosophy of Mathematics Today, Oxford: Clarendon Press, 1998, pp. 131-156. Hanson propone como análisis de las nociones lógicas intuitivas definiciones propias de una semántica de mundos posibles, y que por tanto son en parte representacionales (la propuesta de Hanson posee asimismo un componente interpretacional). Por su parte, Shapiro defiende una interpretación de las definiciones propias de la teoría de modelos según la cual estas involucran un aspecto interpretacional y otro representacional. Según esta interpretación, modelaríamos un lenguaje eligiendo un mundo posible y luego reinterpretando en ese mundo las expresiones no lógicas.
34 Cf. Gómez-Torrente, M., "Logical Truth and Tarskian Logical Truth", en: Synthese, CXVII, 9 (1999), pp. 375-408, p. 384.
35 Cf. Etchemendy, J., The Concept of Logical Consequence, pp. 95-124.
36 En The Concept of Logical Consequence, Etchemendy prefiere formular su crítica usando PR y no PR, ya que el primer principio, a diferencia del segundo, le permite considerar una propiedad lógica (la verdad lógica) a partir de la mera verdad de una fórmula universalmente cuantificada.
37 Cf. ibid., p. 9.
38 Según lo dicho, los requisitos de Etchemendy conducen a lo que puede considerarse una versión de la conocida paradoja del análisis. Dicho brevemente, esta paradoja consiste en que, al exigir una equivalencia conceptual entre explicandum y explicatum, el análisis resultará o bien trivial o bien incorrecto: si los dos conceptos son equivalentes, entonces son en última instancia el mismo concepto y el análisis es trivial; si, por el contrario, ambos conceptos son distintos, el análisis resultará incorrecto (cf. Coffa, J.A., "Dos concepciones de la elucidación filosófica", en: Crítica, VII, 21 (1975), pp. 43-65; Simpson, T.M., "Análisis y eliminación: una módica defensa de Quine", en: Crítica, VII, 21 (1975), pp. 69-83).
39 Cf. Shapiro, S., o.c.; Chihara, C., "Tarskis Thesis and the Ontology of Mathematics", en: Schrin, M. (ed.), o.c., pp. 157-172. A modo de ilustración, las definiciones técnicas de la clase de funciones computables usualmente son consideradas buenas caracterizaciones de la noción intuitiva de computabilidad, al mismo tiempo que se admite que no constituyen análisis conceptuales (cf. Etchemendy, J., The Concept of Logical Consequence, pp. 5-6; Gómez-Torrente, M., "Logical Truth", en: The Stanford Encyclopedia of Philosophy, verano de 2006 (http://plato.stanford.edu/entries/logical-truth/), editada por E.N. Zalta, p. 16).
40 Cf. Gómez-Torrente, M., "Logical Truth and Tarskian Logical Truth", pp. 383-395.
41 Cf. McGee, V., "Two Problems with Tarskis Theory of Consequence", en: Proceedings of the Aristotelian Society, XCII (1992), pp. 273-292, pp. 275-278.
42 Cf. Kreisel, G., "Informal Rigour and Completeness Proofs", en: Lakatos, I. (ed.), Problems in the Philosophy of Mathematics, Ámsterdam: North-Holland, 1967, pp. 138-171.
43 Cf. Gómez-Torrente, M., Forma y modalidad. Una introducción al concepto de consecuencia lógica, Buenos Aires: Eudeba, 2000, pp. 57-65.
44 Por supuesto, el argumento puede fácilmente formularse usando la noción más simple de verdad lógica.
45 Cf. Etchemendy, J., The Concept of Logical Consequence, pp. 148-150.
46 Cf. Gómez-Torrente, M., "The Problem of Logical Constants", en: Bulletin of Symbolic Logic, VIII (2002), pp. 1-37; McFarlane, J., "Logical Constants", en: The Stanford Encyclopedia of Philosophy, verano de 2005 (http://plato.stanford.edu/entries/logicalconstants/), editada por E.N. Zalta; Warmbrōd, K., Logical Constants, en: Mind, CVIII (1999), pp. 503-538.
47 Cf. Gómez-Torrente, M., "The Problem of Logical Constants", pp. 1-5; Hanson, W.H., o.c., pp. 378-379; Warmbrōd, K., o.c., pp. 511-522.
48 Cf. Gómez-Torrente, M., "The Problem of Logical Constants", p. 32.
49 Etchemendy sugiere que el formalismo no ha sido seriamente cuestionado debido a que el análisis tarskiano ha sido de hecho considerado un análisis exitoso a la luz de los dos requisitos referidos en la anterior sección (cf. Etchemendy, J., The Concept of Logical Consequence, pp. 156-159; Reflections on Consequence, pp. 21-24, 34-36). La tesis de que el análisis tarskiano ha sido así considerado es muy dudosa, y más dudosa aun es la tesis de que esta ha sido considerada –aunque sea solo implícitamente– la razón fundamental para aceptar el formalismo. De todos modos no me ocuparé aquí de estas tesis históricas. En cambio, sí quisiera comentar la tesis no histórica de que prácticamente la única razón que tenemos para aceptar el formalismo es el éxito del análisis tarskiano a la luz de los requisitos mencionados.
50 Cf. Etchemendy, J., Reflections on Consequence, pp. 21-24. Las relaciones inferenciales podrían darse incluso utilizando simultáneamente sistemas diferentes de representación. Por ejemplo, los diagramas podrían tener como consecuencias lógicas fórmulas de un lenguaje formal y viceversa.
51 Cf. Gómez-Torrente, M., "The Problem of Logical Constants", pp. 1-5; "Logical Truth", pp. 7-11; Hanson, W.H., o.c., pp. 373-380.
52 Este último principio permitiría excluir del conjunto de las expresiones lógicas a las preposiciones, a las cuales, a pesar de su generalidad, no se ha deseado incluir en este conjunto.
53 Etchemendy considera que el formalismo no es consistente con la inclusión de las lógicas modales dentro del objeto de estudio de la lógica. Pero los principios pragmáticos señalados bien pueden justificar la selección de constantes lógicas presente en estas lógicas, lo cual muestra que ellas son coherentes con el formalismo (cf. Etchemendy, J., Reflections on Consequence, pp. 19-20).