ARTÍCULOS

 

Mundos posibles y paradojas

Possible Worlds and Paradoxes

 

Guillermo Badía

Universidad de La Habana

 

---

Resumen

La definición de un "mundo posible" de Robert Adams es paradójica, de acuerdo con Selmer Bringsjord, Patrick Grim y Cristopher Menzel. Las pruebas de Bringsjord y Grim utilizaban el axioma del Conjunto Potencia; Cristopher Menzel objetó que, mientras este fuese el caso, todavía existía esperanza para la definición de Adams, pero Menzel desempolvó una vieja paradoja de Russell para demostrar que podíamos obtener las mismas conclusiones sin apelar a otra teoría de conjuntos que el Axioma de Separación. Sin embargo, el resultado de Menzel mostraba solo que no existía el mundo actual. En este trabajo intentamos generalizar la paradoja de Russell a mundos posibles arbitrarios sin necesidad de introducir conceptos modales en la discusión.

Palabras clave: paradojas; mundos posibles; teoría de conjuntos.

 

---

Abstract

Robert Adams' definition of a possible world is paradoxical according to Selmer Bringsjord, Patrick Grim and, more recently, Cristopher Menzel. The proofs given by Bringsjord and Grim relied crucially on the Powerset Axiom; Christoper Menzel showed that, while this continued to be the case, there was still hope for Adams' definition, but Menzel he undusted an old russellian paradox in order to prove that we could obtain the same paradoxical consequences without appealing to any other set theory than the Axiom of Separation. Nevertheless, Menzel's result only showed that there was no actual world. In this paper we try to generalize Russell's paradox to arbitrary possible worlds without introducing an irreducible modal component in the discussion.

Key words: paradoxes; possible worlds; set theory.

 

---

1. ¿Qué es un mundo posible?

La introducción en la literatura filosófica de la semántica de mundos posibles por Saul Kripke¹, y su éxito generalizado para dar cuenta de las condiciones de verdad de los enunciados modales, supuso para los filósofos un problema inmediato: si la semántica de Kripke era la adecuada, entonces ¿qué tipo de entidades en nuestra ontología² debían ser identificadas con estos "mundos"³? David Lewis, por ejemplo, propuso en los ochenta su extravagante teoría de los mundos como objetos concretos. Supongamos que un objeto se dice concreto si y solo si dispone de una ubicación espacio-temporal, siendo abstracto en caso contrario. De acuerdo con Lewis: "el mundo que habitamos es una cosa muy inclusiva... No hay nada tan lejos de nosotros como para no ser parte de nuestro mundo. Cualquier cosa, a cualquier distancia, debe ser incluida. De la misma forma, el mundo es inclusivo en el tiempo... Nada es de un tipo tan extraño como para no formar parte de nuestro mundo, bajo la condición de que exista en algún tiempo y a alguna distancia de aquí, o en algún tiempo anterior o posterior o simultáneo con el ahora"⁴. Para Lewis, un "mundo" es una entidad concreta de tal naturaleza que cualquier objeto con una ubicación espacio-temporal, relacionado de alguna manera a ella, constituye una de sus partes, es decir, está incluido por ella. Ahora bien, para Lewis existen "incontables mundos distintos, otras cosas muy inclusivas"⁵, el problema es que estos otros mundos se hallan desvinculados desde el punto de vista espacio-temporal del nuestro, por lo cual, de acuerdo a la última línea del párrafo de Lewis citado anteriormente, no son parte del nuestro.

Sea como fuera, la definición de un mundo posible que estudiaremos aquí, i.e., como un conjunto máximo y posible de proposiciones (o estados de cosas), surge en el contexto del llamado "abstraccionismo" (i.e., la posición filosófica que identifica un "mundo" con una entidad abstracta de cierto tipo contrario a la postura "concretista" de Lewis), y en particular de las manos de Alvin Plantinga y Robert Adams.

Plantinga sostiene que "un mundo posible es un estado de cosas máximo y posible, donde un estado de cosas S es máximo si y solo si para todo estado de cosas S*, ya S incluye a S* o S incluye el complemento ¬S* de S*", o de manera alternativa, indica que "un mundo posible es una proposición máxima y posible: una proposición que es posible, y para cualquier proposición p, ya implica (en el sentido lógico más amplio) a p o implica a ¬p"⁶. Si bien Plantinga, como puede verse, no es partidario de definir un mundo posible en términos de la teoría de conjuntos, sí acepta la existencia para cada mundo posible W del "libro sobre W", i.e., el conjunto de todas las proposiciones implicadas por W⁷, lo cual lo compromete con el mismo tipo de entidades atacadas en estas páginas. Es importante señalar aquí lo que se entiende en la literatura por una proposición y un estado de cosas. Ambas son entidades intensionales (como las propiedades o las relaciones), i.e., se trata de la intensión, el significado, el algo más que nos transmite una expresión lingüística de cierto tipo fuera de su extensión⁸. En el caso de las proposiciones, estas constituyen el significado de las oraciones declarativas. Por ejemplo a la oración "Jantipa es la esposa de Sócrates" le corresponde la proposición Jantipa es la esposa de Sócrates. A oraciones en distintos idiomas puede corresponderles una y la misma proposición si en sentido general ambas expresan el mismo pensamiento. Ahora bien, los estados de cosas son la intensión de expresiones como "Jantipa siendo la esposa de Sócrates" o "Existiendo solo una esposa de Sócrates"⁹. Por su parte, Adams elabora su definición de un "mundo posible" desde una posición "actualista" con respecto a los mundos posibles, i.e., "la postura de que si hay algún enunciado verdadero donde se diga que hay mundos posibles diferentes del actual, estos deben poder ser reducidos a enunciados en los que las únicas cosas que se diga que hay son cosas que hay en el mundo actual y que no son idénticas con objetos posibles no actualizados"¹⁰. En particular, el análisis de Adams consiste en una "reducción del discurso acerca de mundos posibles a un discurso acerca de conjuntos de proposiciones"¹¹. Para Adams las proposiciones son las entidades básicas (i.e., irreducibles) de su ontología, a diferencia de, por ejemplo, Lewis, quien las identifica con conjuntos de "mundos posibles"¹². Adams está en condiciones de realizar semejante reducción introduciendo la idea de un "relato del mundo", i.e., "un conjunto máximo consistente de proposiciones", lo cual para Adams es "un conjunto que tiene como sus elementos a un miembro de cada par contradictorio de proposiciones, tal que es posible que todos sus miembros sean verdaderos de manera simultánea". De esta forma, Adams identifica los "mundos posibles" con "relatos del mundo". Por último, Adams advierte ciertas consecuencias "paradójicas" de su definición: "Notablemente, el desarrollo de una teoría satisfactoria de las proposiciones (o de las intensiones en general) se encuentra también asediado por problemas formales y la amenaza de paradoja. Una de estas amenazas concierne particularmente a [nuestra] teoría de la actualidad. La teoría parece implicar que hay conjuntos consistentes compuestos de un miembro de cada par contradictorio de proposiciones. Es más, se sigue de la teoría, con la suposición de que todo mundo posible es actual en sí mismo, que todo relato del mundo, s, tiene entre sus miembros la proposición de que todos los miembros de s son verdaderos. Aquí nos estamos balanceando en el borde del precipicio de las paradojas"¹³. Es muy probable que el tipo de paradoja que Adams tuviese en mente sea en realidad distinto a las que de hecho se formularon luego, puesto que parece tratarse más bien de una paradoja semántica, como la del mentiroso (que surge de considerar el enunciado "este enunciado es falso") que le debemos al griego Eubulides. No obstante, el pasaje, sin lugar a dudas, sugiere que ciertos resultados (como, por ejemplo, el de Patrick Grim expuesto más abajo en 3) no son tan sorprendentes después de todo.

2. Las paradojas

La paradoja que en estas páginas llamaremos (B) fue expuesta hace varios años por Selmer Bringsjord en un artículo muy breve¹⁴. Se basa de modo crucial en el famoso Teorema de Cantor¹⁵, por lo cual resulta útil dedicar algunas líneas a enunciar este resultado para comodidad del lector. Un postulado elemental de la aritmética de los números cardinales estipula que todo conjunto M tiene una cardinalidad definida determinada por el menor ordinal¹⁶ α tal que existe una biyección de M a α, lo cual, desde un punto de vista intuitivo, equivale a decir que todo conjunto tiene una cantidad de elementos determinados¹⁷. El teorema de Cantor es un descubrimiento fundamental de la teoría de conjuntos con extraordinaria relevancia para la aritmética cardinal. En su forma más conocida, se presenta del modo siguiente: TEOREMA. Para cualquier conjunto M, card(M) < card(℘(M)), i.e., la cardinalidad de M es menor que la cardinalidad del conjunto potencia de M (uno puede convencerse de esto con facilidad si tenemos en cuenta que para un conjunto finito cualquiera de cardinalidad n, la cardinalidad de su conjunto potencia es de 2ⁿ). Ahora bien, lo que Bringsjord pretende demostrar mediante su resultado, valiéndose de una reductio ad absurdum con el teorema de Cantor, es que "simplemente no hay tal cosa como un mundo"¹⁸, al menos en el sentido en que lo define, utilizando la teoría de conjuntos, Robert Adams. En específico, Bringsjord ataca una síntesis de las ideas de Adams y Plantinga, y la formula tanto en términos de estados de cosas como de proposiciones.

Llamamos paradoja a una contradicción que puede ser demostrada (casi siempre a partir de la aceptación de ciertas premisas "plausibles"), de ahí su carácter problemático. En este caso, la paradoja surge de asumir la existencia de un "mundo posible", i.e., un conjunto máximo (i.e., que para cada proposición p, ya p o su negación sean miembros de nuestro conjunto) y posible (i.e., que todos sus miembros pueden ser verdaderos simultáneamente) de proposiciones (o estados de cosas), con el resultado inmediato de que nuestra suposición es absurda. El argumento, (B), es en realidad bastante simple. Si w es un "mundo posible" es obvio que debe tener alguna cardinalidad definida, y en particular card(w) < card(℘(w)). Pero consideremos cualquier subconjunto w* elemento de ℘(w); a w* le corresponde alguna proposición pw* de manera exclusiva (es decir, cualquier otro objeto al que le corresponda la misma proposición es idéntico a w*), e.g., la proposición de que w* es un conjunto (o de modo alternativo, el estado de cosas w* siendo un conjunto). Así pues, es posible definir una función inyectiva de ℘(w) a w tal que a cada w* ∈℘(w) le corresponda la proposición pw*o ¬pw*, de acuerdo a si pw* ∈ w o ¬pw* ∈ w. Se sigue enseguida que card(℘(w)) ≤ card(w), contradiciendo el teorema de Cantor.¹⁹

Como Cristopher Menzel²⁰ ha señalado, el punto esencial para que (B) sea un argumento conclusivo es la suposición de que para cualquier tipo de colección que sea w (ya un conjunto, o alguna otra colección "demasiado grande" para ser considerada un conjunto²¹), esta disponga de una colección de todas sus subcolecciones (y no que w tenga un número cardinal definido, contrario a lo que una inspección superficial de la prueba de (B) pudiese indicarnos). Pues de la existencia de esta colección se sigue que "uno puede deducir la negación del teorema de Cantor, que en su forma más común no dice nada acerca de la cardinalidad (solo dice que existe una función inyectiva deS a ℘(S), pero que lo inverso no es el caso), y es aplicable de manera general a cualquier colección que tenga una correspondiente "colección potencia"²². Resulta que la formulación del teorema de Cantor que hemos analizado en estas páginas no es la que Menzel tiene en mente en el pasaje anterior, pero podemos adaptarla con facilidad. Como un caso particular de otro famoso teorema de la teoría de conjuntos, denominado teorema de Bernstein²³ (por Felix Bernstein), tenemos que: si hay una inyección de S a ℘(S) y una de ℘(S) a S, entonces debe existir una biyección entre ℘(S) y S, lo que significaría que ℘(S) y S tienen la misma cardinalidad. Pero Cantor demostró en su teorema que de hecho existe una inyección de S a ℘(S), pero no una biyección entre ℘(S) y S, de modo que por contraposición y silogismo disyuntivo con el teorema de Bernstein, se sigue que no hay una inyección de ℘(S) a S.

Por su parte, Patrick Grim había publicado ya²⁴ una paradoja similar a (B)²⁵, que si bien encerraba una consecuencia más modesta con respecto a la discusión de los "mundos posibles"²⁶, parecía incluso filosóficamente más sugerente²⁷: no existe el conjunto de todas las verdades. Nótese que, de acuerdo a la teoría de mundos de Adams, este conjunto sería nada menos que el mundo actual, del cual cada uno de nosotros somos habitantes. Grim nos pide en primer lugar que consideremos el conjunto T de todas las verdades. Pero de la existencia de este conjunto se sigue que debe haber un conjunto potencia de T. Ahora bien, es fácil advertir que a cada elemento de este conjunto potencia, i.e., a cada subconjunto S de T, le correspondería alguna verdad, por ejemplo (siguiendo a Grim), t_i ∈S (o t_i ∉S según el caso), donde ti se trata de un elemento fijo cualquiera de T. Esta verdad le correspondería a cada S de forma exclusiva, de lo que se sigue que existe una inyección de ℘(T) a T, pero, como se ha visto en el párrafo anterior, eso es imposible de acuerdo al teorema de Cantor²⁸. Grim concluye que habría "más verdades que miembros de T", por lo cual "algunas verdades deben haber sido dejadas fuera, y por tanto T no puede, como hemos asumido, ser el conjunto de todas las verdades"²⁹.

El debate acerca de estos resultados continuó con Menzel³⁰ y Grim³¹. Menzel³² sostuvo que uno podía rechazar el Axioma del Conjunto Potencia³³ sobre el que depende (B), y adoptar una versión de la teoría axiomática de conjuntos Zermelo-Fraenkel (ZF) sin este axioma³⁴. Por su parte, Grim³⁵ intentó probar que su propia paradoja³⁶ podía obtenerse sin el Axioma, pero, como Menzel³⁷ ha señalado, la prueba de Grim era bastante dudosa (pues utiliza el Axioma del Conjunto Potencia de modo implícito, o, en su defecto, necesita una buena porción más de la teoría de conjuntos que hasta el momento había sido empleada en la discusión para demostrar su tesis). En este mismo artículo, Menzel reconoce haber estado equivocado, y rescata un resultado de Russell (no existe el conjunto de todas las proposiciones), modificándolo para demostrar que no existe el conjunto de todas las verdades (i.e., la paradoja de Grim³⁸) sin más teoría de conjuntos que el Axioma de Separación³⁹ de ZF. El argumento se construye sobre las siguientes premisas:

1. Existe un conjunto de todas las verdades T.

2. Para cualquier subconjunto S de T, hay una verdad que lo identifica ps.

3. Para cualesquiera subconjuntos S y S´ de T, si pS = pS´, entonces S = S´.

Ahora bien, supongamos que S es un subconjunto cualquiera de T, ya pS ∈ S o pS ∉ S. Definamos entonces un conjunto R que contenga a todas las pS del segundo tipo (i.e., todas las x tal que exista algún subconjunto S de T y x sea pS, y x no pertenezca a S; en símbolos, x ∈R si y solo si ∃S⊆T (x=pS & x ∉ S)). Como T es el mundo actual, R es un subconjunto de T, y de acuerdo a (ii) le corresponde una proposición pR. Si pR ∈ R, entonces pR ∉ R por la condición de membresía en R. Si pR ∉R, entonces como R es un subconjunto de T y para todo subconjunto S de T si pR=pS entonces pR ∈S, pR ∈R. Hemos demostrado que pR ∈R si y solo si pR ∉R, lo cual es una contradicción.

3. El resultado Russell-Menzel generalizado

Menzel⁴⁰ señala en una nota al pie que el argumento con el que hemos finalizado el apartado anterior puede generalizarse para "mundos posibles arbitrarios" solo si estipulamos que pS es alguna proposición necesaria acerca de S en (ii), lo cual garantizaría su pertenencia a cualquier conjunto máximo y posible de proposiciones. Esto se debe a que la semántica de mundos posibles de Kripke estipula que un enunciado es necesario en el mundo actual w si y solo si es verdadero en todos los mundos posibles w´ a los que tenemos acceso desde w. De modo que la elección de pS como una proposición necesaria de T (nuestro mundo actual) le permite a Menzel utilizar la paradoja de Russell en un mundo posible W (no-actual), puesto que pS tendría que ser un miembro de W por la semántica que hemos asumido. Lo que pretendemos demostrar aquí es que una versión de la paradoja de Russell puede elaborarse para mundos posibles arbitrarios, y no solo para el mundo actual, sin necesidad de introducir conceptos modales irreductibles en ella⁴¹, con lo cual cualquier posible alternativa de evasión para el ataque russelliano a la definición de Adams se desvanece. Esto revela, definitivamente, qué tipo de entidades no deberían ser identificadas con "mundos posibles". Nuestra prueba es bastante simple. Utilizando las premisas del argumento de Bringsjord, tal y como el propio Menzel⁴² las enumera –vale decir, (i) existe un mundo posible w, (ii) a cualquier subconjunto S de w le corresponde una proposición pS, (iii) cada proposición p tiene un complemento ¬p, y (iv) si pS' y pS son idénticas, o ¬pS' y ¬pS lo son, entonces S es idéntico a S'–, podemos definir por el Axioma de Separación el conjunto R donde para toda x ∈ w,

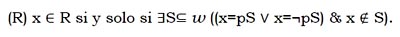
Pero R es un subconjunto de w, y de acuerdo a (ii) le corresponde una proposición pR, y por (iii), pR tiene un complemento ¬pR. Con lo cual, existen dos posibilidades: pR ∈ w o ¬pR ∈ w, por la maximalidad de w. Supongamos lo primero, i.e., pR ∈ w. ¿Es pR un miembro de R? Si lo es, entonces pR ∉ R según (R), y si no lo es, como pR ∈ w, por (R) para todo subconjunto S de w si pR=pS o pR=¬pS, entonces pR ∈S, y se sigue de inmediato que pR ∈R. Por lo tanto, hemos probado una contradicción, así que debe ser el caso que pR ∉ w. Como consecuencia de esto, ¬pR ∈w por silogismo disyuntivo y la maximalidad de w. Entonces, preguntémonos: ¿es ¬pR un miembro de R? Si lo es, entonces ¬pR ∉ R según (R), y si no lo es, como ¬pR ∈ w, para todo subconjunto S de w si ¬pR=pS o ¬pR=¬pS entonces ¬pR ∈S, de lo que se sigue que ¬pR ∈R. De esta forma, llegamos a la conclusión de que pR ∉ w y ¬pR ∉w, contradiciendo la maximalidad de w. Como nuestra suposición de la existencia de w nos ha conducido a una auténtica contradicción, la rechazamos. La conclusión evidente a extraer de nuestra discusión es que simplemente no todas la «colecciones» con las que tratamos en filosofía se comportan bien desde un punto de vista matemático. Uno no debería pretender "reducir" ciertas entidades (como los «mundos posibles») que pueden ser halladas en nuestra ontología a objetos matemáticos, ni siquiera en pos de la claridad y la precisión (sin dudas la definición de Adams es natural e intuitiva a la hora de considerar el concepto de "verdad en un mundo posible", el cual coincidiría en esta con el de membresía). La respuesta ha de encontrarse en otro sitio, fuera de la teoría de conjuntos⁴³.

 

---

1 Cf. Kripke, S. A., "A Completeness Theorem in Modal Logic", en: Journal of Symbolic Logic, XXIV, 1 (1959), pp. 1-14; "Semantical Considerations on Modal Logic", en: Acta Philosophica Fennica, 16 (1963), pp. 83-94.

2 En estas páginas debe entenderse "ontología" en el mismo sentido de la discusión metafísica contemporánea, como una respuesta a la pregunta ¿qué entidades son las que hay? Es probable que la exposición más famosa de esta idea sea la de Quine (cf. Quine, W.V., "On What There Is", en: From a Logical Point of View, 2da ed., Cambridge: Harvard University Press, 1961, pp. 1-19.)

3 De acuerdo con C. Menzel, a pesar de que la noción de mundo posible "ha estado en el vocabulario filosófico al menos desde Leibniz, solo ha quedado firmemente arraigada en la filosofía contemporánea con el desarrollo de la semántica de mundos posibles para los lenguajes de la lógica modal" (Menzel, C., "Possible worlds", manuscrito).

4 Lewis, D., On the Plurality of Worlds, Oxford: Blackwell, 1986, p. 1; el énfasis es nuestro.

5 Ibid., p. 2.

6 Plantinga, A., "Two Concepts of Modality", en: Davidson, M. (ed.), Essays in the Metaphysics of Modality, Nueva York: Oxford University Press, 2003, p. 195.

7 Cf. Plantinga, A., The Nature of Necessity, Oxford: Clarendon Press, 1974, pp. 44-46.

8 Por ejemplo, si decimos "Barack Obama es el presidente de los Estados Unidos", la extensión de dicha oración es el valor de verdad "verdadero", mientras que su intensión es la proposición que se expresa mediante la oración. O en el caso del predicado "_ es un filósofo", su extensión es el conjunto de los objetos que lo satisfacen, e.g. Sócrates, Platón, Aristóteles, etcétera, mientras que su intensión es la propiedad de ser un filósofo. En lógica esta distinción entre extensión e intensión adquiere la forma de la validez o no de ciertos principios de sustitución salva veritate en los lenguajes formales. Por ejemplo, en la lógica proposicional trabajamos con contextos extensionales, donde el principio de remplazo "a partir de la premisa φ ↔ ψ se sigue que χ[φ] ↔ χ[ψ]” es válido. Consideremos el siguiente ejemplo: la oración "(1) Barack Obama es el presidente de los Estados Unidos si y solo si (2) Jantipa era la esposa de Sócrates" es verdadera en la lógica proposicional puesto que tanto (1) como (2) lo son. Así pues, "no es caso que (1) si y solo si no es caso que (2)" también lo es, puesto que "no es caso que (1)" y "no es caso que (2)" son ambos enunciados falsos. Por su parte, en la lógica modal clásica este principio no es válido (está lejos de ser evidente que del hecho de que "(1) si y solo si (2)" se siga que "es necesario que (1) si y solo si es necesario que (2)"), y tiene que ser replanteado en la forma "si φ ↔ ψ es una verdad lógica, entonces χ[φ] ↔ χ[ψ] también lo es", i.e., nos enfrentamos a un contexto intensional. Este tema es bastante abordado en la literatura, e.g., Carnap (cf. Carnap, R., Meaning and Necessity, Illinois: The University of Chicago Press, 1948) lo trabaja ampliamente, Menzel (cf. Menzel, C., Possible Worlds (manuscrito), 2012), ofrece una ilustrativa introducción a sus complejidades filosóficas, y Kleene (cf. Kleene, S. C., Mathematical Logic, Nueva York: John Wiley and Sons, 1968) suministra un conciso resumen.

9 Ejemplos de Plantinga son: "No existiendo leones en Australia", "Sócrates siendo sabio", "7+5 siendo igual a 12" (Plantinga, A., "Two Concepts of Modality", en: Davidson, M. (ed.), Essays in the Metaphysics of Modality, Nueva York: Oxford University Press, 2003, p. 194).

10 Adams, R., "Theories of Actuality", en: Nous, 8 (1974), pp. 31-211, p.224.

11 Ibid.

12 Lo cual se inspira de manera evidente en la semántica de Kripke (cf. Kripke, S. A., "A Completeness Theorem in Modal Logic", en: Journal of Symbolic Logic, XXIV, 1 (1959), pp. 1-14; "Semantical Considerations on Modal Logic", en: Acta Philosophica Fennica, 16 (1963), pp. 83-94.).

13 Adams, R., o.c, p. 229.

14 Bringsjord, S., "Are There Set Theoretic Possible Worlds?", en: Analysis, 45, 1 (1985), p. 64.

15 Nombrado en honor de su descubridor: Georg Cantor (1845-1918).

16 En la teoría de conjuntos, el concepto de un "ordinal" es un artificio teórico diseñado para servir de análogo a la idea de "número natural" en la aritmética. Los ordinales son cierto tipo de conjuntos (en particular, conjuntos transitivos bien ordenados), por ejemplo ∅(el conjunto vacío) es el ordinal denotado por 0, {∅} el denotado por 1, {∅, {∅}} el denotado por 2, etcétera. Con su ayuda, es posible extender la idea de "número" en el reino de lo transfinito (para enumerar colecciones, por decirlo de algún modo, más grandes que las infinitas). De hecho, haciendo uso del mismo somos capaces de obtener una definición muy precisa de "número natural", viz., los ordinales finitos.

17 Por ejemplo, sea el conjunto M = {Sócrates, Platón, Aristóteles}, card(M) = 3. El número cardinal de un conjunto M es una noción que "abstraemos" de todos los conjuntos entre los que se puede establecer una correspondencia biunívoca con nuestro conjunto M (cf. Kleene, S. C., Mathematical Logic, Nueva York: John Wiley and Sons, 1967, p. 184).

18 Bringsjord, S., "Are There Set Theoretic Possible Worlds?", p. 64.

19 Un argumento similar surge en el contexto del ersatzismo lingüístico de David Lewis. Esta postura es simplemente el intento de Lewis de ofrecer una teoría menos "extravagante" que la de los mundos posibles como objetos concretos, y sugiere que quizá podrían tratarse de conjuntos de oraciones (mundos ersatz, i.e., sustitutos). El único problema es que, asumiendo que existiese un espacio euclidiano con todos sus puntos llenos por materia, si cada forma en que el mundo pudiera ser determina un mundo posible, la cantidad de mundos ersatz es insuficiente. Como lo explica Anthony Roy para "el conjunto de todos los números naturales N, la cardinalidad de los puntos en un espacio euclidiano, como la de los números reales, es card(℘(N))…; de modo que hay ℘℘(N) conjuntos de puntos en el espacio y, de acuerdo a nuestra suposición, la misma cantidad de formas para distribuir la materia. Pero solo existen N secuencias finitas de símbolos en un vocabulario finito; …de manera que el número de mundos es como máximo ℘(N). Así que mediante el Teorema de Cantor, existen más formas de las que puede ser el mundo que mundos ersatz" (Roy, A., "Modality", en: The Continuum Companion to Metaphysics, 2012, (en imprenta), pp. 46-66, p. 64).

20 Menzel, C., "On Set Theoretic Possible Worlds", en: Analysis, 46, 2 (1986), pp. 68–72, p. 9.

21 Por ejemplo, una "clase", que carece de una cardinalidad definida (ser "demasiado grande") en la teoría axiomática de conjuntos suplementada con términos para "clases", de acuerdo al postulado fundamental de la aritmética cardinal, no es un conjunto (cf. Menzel, C., "On the Iterative Explanation of the Paradoxes", en: Philosophical Studies, 49 (1986), pp. 37–61, p. 44).

22 Menzel, C., "On Set Theoretic Possible Worlds", p. 9.

23 La prueba de este resultado es algo compleja (cf. Kleene, S. C., Introduction to Metamathematics, Amsterdam: North Holland Pub. Co., 1952, pp. 11-12; Devlin, K., The Joy of Sets, Nueva York: Springer-Verlag, 1979, p. 77), por lo que no resulta pertinente exponerla aquí. El teorema básicamente dice lo siguiente (donde A y B son conjuntos): si A ≤ B y B ≤ A entonces A es equipolente a B, i. e., comparten la misma cardinalidad. Pero recordemos que A ≤ B si y solo si existe una inyección de A hacia B.

24 Cf. Grim, P., "There is No Set of All Truths", en: Analysis, 44, 4 (1984), pp. 206–208.

25 Dependiendo también de modo crucial sobre el Axioma del Conjunto Potencia.

26 De acuerdo a Bringsjord (Bringsjord, S., "Grim on Logic and Omniscience" en: Analysis, 49, 4 (1989), pp. 186–189, p. 186), la paradoja de Grim es en realidad una conclusión intermedia que se sigue de algunas variaciones en la prueba de (B).

27 Grim introduce su resultado apuntando que una "importante consecuencia filosófica del teorema de Cantor ha pasado inadvertida" (Grim, P., "There is No Set of All Truths", p. 206).

28 Grim originalmente plantea su razonamiento en términos de tamaño relativo. En primer lugar, de acuerdo a la aritmética cardinal, card(M) ≤ card(N) si y solo si M ≤ N, i.e., si y solo si existe una biyección entre M y algún subconjunto N1 de N; mientras que card (M) < card (N) si y solo si M < N, i. e., si y solo si M y N son tales que hay una inyección de M a N pero no hay ninguna inyección de N a M. Pero una biyección existe en el argumento de Grim entre ℘(T) y el subconjunto de T que comprende todas las verdades ti ∈S ∈℘(T) o ti ∉ S ∈℘(T), como las descritas arriba. Así, tenemos que ℘(T) ≤ T, lo cual contradice T < ℘(T) (el teorema de Cantor).

29 La aplicación a la discusión sobre la incoherencia de la definición de un mundo posible es solo una de las tantas que hace Grim de su resultado. Por ejemplo, en otro sitio propone un argumento basado en su paradoja para refutar la existencia de Dios. Grim sostiene que de "haber un ser omnisciente, lo que ese ser conociese constituiría un conjunto de todas las verdades. Pero no puede haber un conjunto de todas las verdades, de modo que no puede existir un ser omnisciente" (citado en: Bringsjord, S., "Grim on Logic and Omniscience", p. 186). El problema fundamental con este argumento, desde nuestro punto de vista, es que la primera oración de Grim está lejos de ser evidente. No hay ninguna razón por la cual de la existencia de un ser omnisciente se siga que el conjunto de todo lo que ese ser conoce existe, al menos no en la teoría axiomática de conjuntos ZF.

30 Cf. Menzel, C., "On Set Theoretic Possible Worlds".

31 Cf. Grim, P., "There is No Set of All Truths".

32 Cf. Menzel, C., "On Set Theoretic Possible Worlds".

33 Este axioma de ZF postula que si existe un conjunto M cualquiera, entonces también existe ℘(M).

34 En particular, Menzel propone como candidata la teoría presentada en Menzel, C., "On the Iterative Explanation of the Paradoxes", en: Philosophical Studies, 49 (1986), pp. 37-61.

35 Cf. Grim, P., "There is No Set of All Truths".

36 Cf. Grim, P., "On Sets and Worlds: A Reply to Menzel", en: Analysis, 46, 4 (1986), pp. 186-191.

37 Cf. Menzel, C., "Sets and Worlds Again", en: Analysis 72, 2 (2012), pp. 304-309.

38 Cf. Grim, P., "On Sets and Worlds: A Reply to Menzel".

39 Si se dan un conjunto M y una propiedad P, podemos "separar" de M el subconjunto de aquellas x ∈M que satisfacen la propiedad P (expresable en el lenguaje de ZF, el cual se compone del lenguaje de la lógica de primer orden con identidad y algún predicado distinguido representado como "∈", la relación binaria de pertenencia) significativa para los miembros de M (i.e., que para cualquier miembro x de M ya sea el caso que x satisfaga P o que x no satisfaga P).

40 Cf. Menzel, C., "Sets and Worlds Again", p. 6; Bueno, O. y otros, Avoiding Russell-Kaplan Paradoxes: Worlds and Propositions Set Free, 2012, (manuscrito), p. 5.

41 Nótese que la aparición de estos nos conduce, si no a un círculo vicioso, al menos a una situación indeseable, puesto que la discusión original se basaba por completo en el hecho de que la semántica de mundos posibles era la apropiada para dar cuenta de las condiciones de verdad de los enunciados modales.

42 Cf. Menzel, C., "Sets and Worlds Again", p. 2.

43 Por ejemplo, una sugerente solución metafísica al problema de los mundos posibles se encuentra en O. Bueno y otros, Avoiding Russell-Kaplan Paradoxes: Worlds and Propositions Set Free, 2012, (manuscrito).