Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista de Gastroenterología del Perú
versión impresa ISSN 1022-5129
Rev. gastroenterol. Perú vol.34 no.1 Lima ene. 2014
Artículo de revisión
Introducción al meta-análisis tradicional
Introduction to traditional meta-analysis
Rafael Bolaños Díaz 1,2a, María Calderón Cahua 2,3,a
1 Unidad de Análisis y Generación de Evidencias en Salud Pública (UNAGESP), Instituto Nacional de Salud. Lima, Perú.
2 Organización Médica para el Desarrollo de la Salud (ODDS PERU). Lima, Perú.
3 Universidad Peruana Cayetano Heredia (UPCH). Lima, Perú.
a MD, MSc
RESUMEN
Actualmente existe un crecimiento sostenido de la información científica en medicina que imposibilita que se tenga conocimiento de la totalidad de los artículos publicados. Los meta-análisis son estudios que tienen la finalidad de compilar toda la información disponible, agrupándola según un tema específico y evaluándola a través de herramientas de calidad metodológica. El objetivo principal consiste en estimar un tamaño de efecto resumen después de combinar los resultados individuales de cada estudio seleccionado bajo un análisis estadístico suficientemente válido. El siguiente artículo tiene por finalidad describir los conceptos básicos y fundamentales del meta-análisis tradicional, tomándose esta información como insumo para las próximas revisiones sobre “métodos avanzados en meta-análisis” que se están utilizando a partir de éste, tal como el meta-análisis indirecto o el meta-análisis network (meta-análisis en red).
Palabras clave: Metanálisis; Acceso a la información; Proteínas publicaciones científicas y técnicas (fuente: DeCS BIREME).
ABSTRACT
Currently there is a steady growth of scientific information in medicine which unable complete knowledge of all the articles published. Meta-analysis are studies that aim to compile all available information, grouping them according to a specific outcome, and evaluating it through methodological quality tools. Its main objective is to estimate a summary effect size after combining the individual results of each study selected under a sufficiently valid statistical analysis. The following article is to describe the basic and fundamental concepts of traditional meta-analysis, taking this information as input for future reviews of “advanced methods in meta-analysis”, such as indirect meta-analysis or network analysis.
Key words: Meta-analysis; Access to information; Scientific and technical publications (source: MeSH NLM).
INTRODUCCIÓN
En 1992 el grupo “Evidence-Based Medicine Working Group” introdujo el concepto de Medicina Basada en Evidencia (MBE) por primera vez (1). A partir de ese momento, la práctica médica ha sufrido cambios dramáticos en donde las decisiones clínicas son basadas en la mejor evidencia existente juzgada a partir de la calidad metodológica de ésta y no solamente en la experiencia del médico tratante (2). El resultado final es que los profesionales de salud nos enfrentamos día a día a una cantidad numerosa de información que hace imposible la lectura de ésta en su totalidad y una toma oportuna de las decisiones clínicas. Por ejemplo, sólo haciendo una búsqueda en Pubmed en los últimos 5 años se han encontrado 6426 artículos sobre adenocarcinoma pancreático (Palabra clave “pancreatic adenocarcinoma”) de los cuales 360 son ensayos clínicos (EC) y 150 son revisiones sistemáticas (RS) con o sin meta análisis (MA).
La investigación clínica tiene como objetivo obtener resultados claros y confiables que puedan ser utilizados para el manejo del paciente y posiblemente como base para guías de prácticas clínicas, pero los ECs unitariamente no siempre llegan a esta meta y dan resultados que frecuentemente se contrastan entre ellos (3,4). El MA, si es correctamente usado, contribuye a alcanzar dicha meta y permite una evaluación crítica de los estudios bajo consideración (4,5). Es decir, el MA proporciona un único resultado combinado basado en diferentes estudios sobre el mismo tema y con la misma metodología. Además el MA contribuye en muchos aspectos de la investigación clínica como por ejemplo: aumenta el poder estadístico de la comparación, mejora la estimación del efecto del tratamiento, combina resultados de estudios contradictorios, contesta nuevas preguntas, analiza subgrupos de sujetos seleccionados de diferentes estudios, analiza tendencias, define áreas en las que se necesita más investigación, entre otros (2). Sin embargo, aunque los meta-análisis están considerados dentro de los modelos de alta jerarquía epidemiológica es importante recordar que tienen algunas limitaciones propias del modelo observacional, incluyendo su naturaleza retrospectiva y agregada además de la pérdida de aleatorización.
El objetivo de esta serie de revisiones sobre MA es procede a realizar la llamada Revisión Sistemática (RS) proporcionar al investigador, que no necesariamente per se. En esta etapa se realiza un proceso de selección está familiarizado con matemáticas y estadística, los principios básicos para entender el poder del MA y los instrumentos esenciales para realizar uno. Dada la complejidad del tema, proporcionaremos ejemplos de MA basados en ECs con variables desenlace binaria (dos resultados, por ejemplo: Mejoró con el tratamiento, si o no). En este primer capítulo revisaremos los conceptos esenciales relacionados con MA tradicional, conceptos importantes que nos servirán para entender luego el MA indirecto y el MA network que se desarrollarán en las siguientes publicaciones
CÓMO PLANEAR UN METAANÁLISIS
El primer paso para realizar un MA es definir la variable desenlace que se analizará y que tiene que encontrarse en todos los EC seleccionados (6). Después se pueden incluir otras variables que son llamadas variables secundarias y que tienen la posibilidad de no ser consideradas en cada uno de los artículos a analizar
(6,7). El proceso general para la elaboración de un MA se resume en el Figura 1. 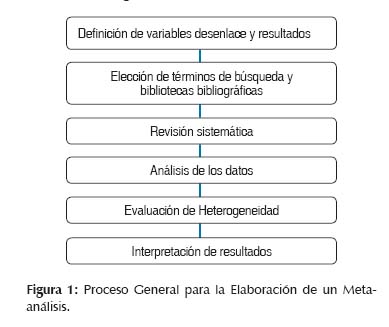
Es importante resaltar que en las primeras fases del MA se seleccionarán la mayor parte de artículos posibles y durante el proceso se irán discriminando según criterios específicos. Para este primer momento es importante definir además en donde se buscará la información y cómo se realizará esta búsqueda. Actualmente se cuenta con muchas bibliotecas de bibliografía médica, siendo las más reconocidas Medline, Embase y Pubmed (8). Con el objetivo de hacer una búsqueda efectiva es importante que se elijan las palabras clave precisas para identificar el tema de nuestra investigación. Una metodología siempre importante es definir la pregunta PICO (Población-Intervención-Comparación-Outcome) de cada estudio (9).
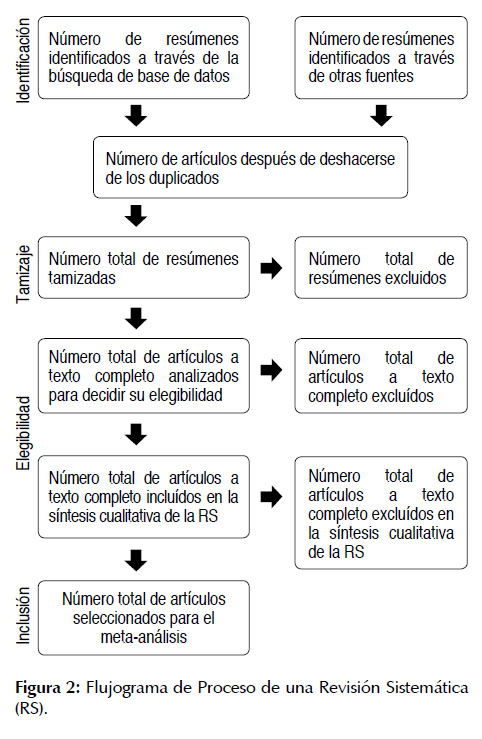
Después de haberse hecho la primera búsqueda tomando en cuenta lo anteriormente descrito, se procede a realizar la llamada Revisión Sistemática (RS) per se. En esta etapa se realiza un proceso de selección que se describe específicamente en la Figura 2.
PROCESAMIENTO ESTADÍSTICO
Después de haber concluido la RS, se pasa a elaborar una tabla en donde los resultados de cada estudio seleccionado se resumirán. Los resultados de un EC pueden ser expresados como Odds Ratio (OR), Riesgo Relativo (RR) o Diferencia de Riesgos (dR). Este será el insumo final para el MA (7).
Antes de combinar los resultados, se debe asumir que cada uno de los estudios tiene un tamaño de efecto. Como se dijo antes, el MA es un procedimiento que permite la agregación de resultados de múltiples estudios y proporciona pesos a los resultados de cada estudio de acuerdo a su precisión. Esta precisión es estimada de acuerdo a la amplitud de la dispersión, a la cual se le llama varianza (7).
Para entender la siguiente parte, es necesario detenernos a definir que es “tamaño de efecto”. El tamaño de efecto puede ser real u observado. El tamaño real es el tamaño de efecto en la población del estudio si esta fuera infinitamente larga (es decir si no tuviera error en el muestro), mientras que el tamaño observado es el que se obtiene de la muestra presentada en el estudio.
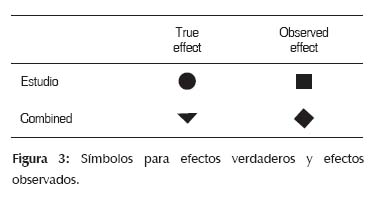
La mayoría de veces, el MA tradicional se sustenta en dos modelos estadísticos, el modelo de efectos fijos y el modelo de efectos aleatorios. A continuación explicaremos esto de forma gráfica y utilizando los símbolos presentados en la Figura 3.
Modelo de Efectos Fijos: (6,7)
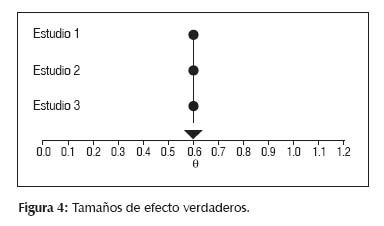
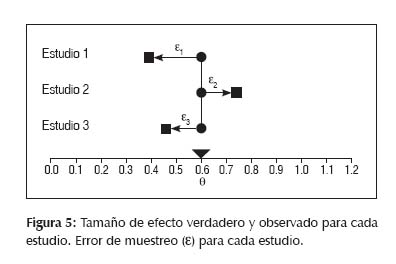
Bajo este modelo se asume que todos los estudios del MA comparte un tamaño de efecto común verdadero. Entonces el tamaño de efecto verdadero es el mismo en todos los estudios. En la Figura 4 se explica esto de una manera gráfica observando que los 3 estudios presentados tienen el mismo tamaño de efecto verdadero (θ) mientras que en la Figura 5 observamos que se grafican además los efectos observados de cada estudio (obtenidos del artículo seleccionado) y se ve que no son iguales a los efectos reales, dando esta diferencia un error considerado error de muestreo ε.
Modelos de efectos Aleatorios: (6,7)
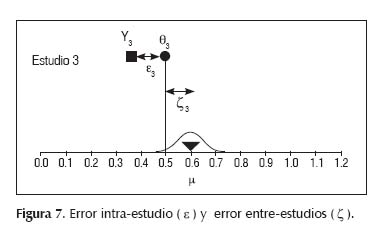
Como se describió en la parte anterior el modelo de efectos fijos empieza con asumir que el tamaño de efecto es el mismo en todos los estudios. Sin embargo, en muchas ocasiones asumir esto es imposible, ya que no podemos tener dos estudios exactamente iguales y generalmente no hay razón para asumir esto. Una manera para afrontar esta variación entre los estudios es la utilización del modelo de efectos aleatorios. En este modelo nosotros asumimos que los efectos verdaderos están bajo la distribución normal (Figura 6). De esta forma tenemos que los efectos observados de cada estudio caen dentro de una curva normal de efectos verdaderos en el rango de 0,5 a 0,7 (tomando el ejemplo empleado en la Figura 5 y teniendo un promedio de efectos verdaderos μ).
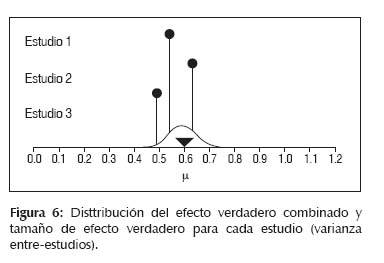
En este ejemplo, tomando sólo el estudio 3 podemos ver que éste tiene además un tamaño de efecto observado donde aparece el error de muestreo εdescrito anteriormente (varianza intra-estudio), pero además aparece otra variación ζ
producida por la diferencia entre el efecto verdadero del estudio y el promedio de efectos verdaderos de la distribución normal (varianza entre-estudios).La ponderación de los estudios es diferente según el modelo que se adopte para el meta-análisis. El peso de cada estudio depende de su tamaño de muestra (n) y de su varianza, según la siguiente ecuación:
Precisión = n / varianza
Por tanto, para el modelo de efectos fijos los estudios con mayor precisión serán los de mayor ponderación, y así el peso de un estudio i se relaciona inversamente con su varianza σ i 2 (VARi), producto del error de muestreo, de acuerdo a la siguiente ecuación (Figura 8):

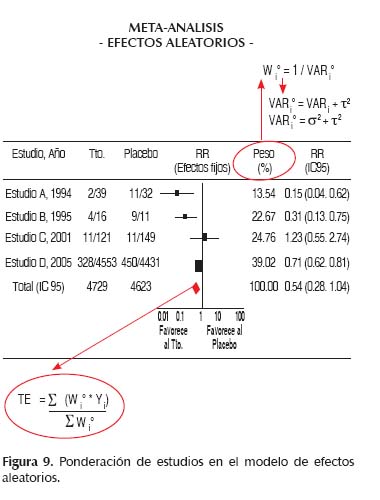
En el modelo de efectos aleatorios el peso de un estudio i dependerá de la suma de sus dos varianzas, tal como lo vimos en la Figura 7, es decir, la varianza intraestudio σ2 (error aleatorio de muestreo) y la varianza entre-estudios τ 2. Un método para estimar el τ2 es el método de momentos (o método de DerSimonian & Laird), tal como sigue:
Es decir, en el modelo de efectos aleatorios el peso de cada estudio (Wi) será inversamente proporcional a su varianza aumentada (VARi°), la misma que tiene dos componentes (σ2 y τ2).
En general, siendo Yi el tamaño de efecto del estudio i y Wi el peso del mismo estudio, el tamaño de efecto combinado (TE) será igual a la sumatoria de los productos Wi*Yi (∑Wi*Yi), dividido entre la sumatoria de los pesos Wi (∑Wi).
Como puede observarse en las Figuras 8 y 9, según el modelo del meta-análisis (efectos fijos o efectos aleatorios) el cálculo de TE varía según la forma de ponderar cada estudio, es decir, considerando sólo σ2 (efectos fijos) o la suma de σ2 y τ2 (efectos aleatorios).
SESGOS EN EL METAANÁLISIS
Hay múltiples sesgos que se deben tomar en cuenta al momento de realizar un MA. Entre éstos los investigadores sólo toman en cuenta el sesgo de publicación, mientras que los otros tipos de sesgos son ignorados o no tomados con importancia. Por esta razón en esta sección desarrollaremos los
métodos para detectar y controlar el sesgo de publicación (10,11).El sesgo de publicación básicamente consiste en la publicación o no de los datos obtenidos en un estudio de investigación científica. Entonces este sesgo representa un riesgo para la validez de cualquier MA por la publicación selectiva en base a sus hallazgos (11-13).
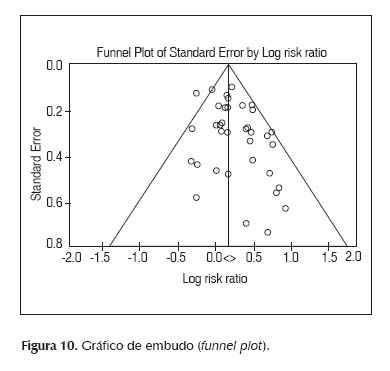
Hay muchas formas de evaluar el sesgo de publicación, ya que este efecto no puede ser eliminado. Entre los más usados están: el método gráfico de Light y Pillemer (funnel plot) en donde un gráfico es calculado usando los tamaños de efecto y los tamaños de muestra de cada estudio (7). De esta forma, los puntos tenderían a distribuirse en forma de un embudo invertido. Si, por el contrario, existiese un sesgo de publicación, de los estudios de menor tamaño muestral solo se publicarían aquellos que encontrasen diferencias significativas entre los grupos, de forma que la nube de puntos aparecería deformada en uno de sus extremos (14). Esta representación se observa en la Figura 10.
Existen otras técnicas estadísticas como la prueba de Begg o de Egger implementadas en la mayoría de los programas computacionales para la realización de MA que permiten evaluar de una manera más objetiva la existencia de un posible sesgo de publicación, pero no ahondaremos en estas.
Por otro lado, algunos expertos (15) consideran que vale más invertir en la actualización de las revisiones que en una búsqueda exhaustiva de la data no publicada. La inclusión de estudios con poca muestra y bajo poder estadístico aumenta la probabilidad de resultados no significativos y de su no-publicación, sin embargo, esta situación no desmerece los resultados ya que los MAs que incluyen estudios de bajo poder (50% en promedio) concuerdan estrechamente con la diferencia “real” en el tamaño de efecto de la intervención en estudio, aún en presencia de sesgo de publicación. Estudios previos han demostrado que los MAs de ensayos pequeños tienen resultados muy similares a aquellos provenientes de MA de grandes ensayos sobre la misma intervención. De acuerdo a Van Driel et al., la pregunta clave no debería centrarse en la existencia de sesgo de publicación sino en el verdadero impacto de este sesgo (15).
INTERPRETACIÓN DE LOS RESULTADOS
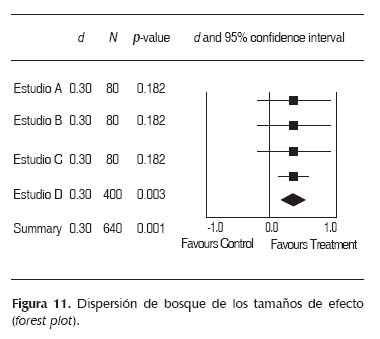
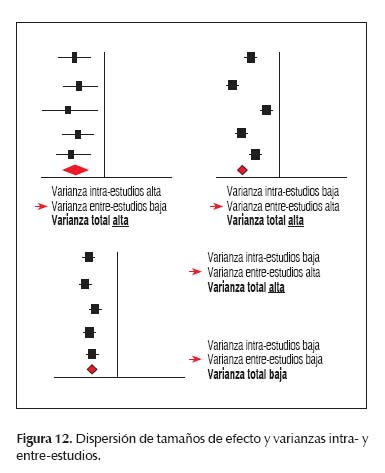
Los resultados obtenidos se presentan a través de un forest plot como se muestra en las Figura 11 y 12. Un forest plot es el resumen de todos los resultados en cada estudio y el resultado combinado final (16,17).
HETEROGENEIDAD
Después de obtener los resultados se debe analizar la heterogeneidad de los mismos. Se trata de analizar hasta qué punto los resultados de los diferentes estudios pueden combinarse en una única medida. Diferencias en el diseño del estudio, las características de la población, etc. pueden llevar a resultados muy diferentes y comprometer los resultados del MA (18).
La detección de la heterogeneidad se puede hacer a través del análisis de los intervalos de confianza, examinando la sobreposición de éstos a simple vista (Figura 12). También se puede utilizar un test formal como el chi cuadrado, utilizando una prueba de hipótesis, en donde se evalúa si las diferencias observadas son compatibles sólo con el azar. También se puede evaluar el impacto de la heterogeneidad en el estimado agregado de inconsistencia I2 (I2>50%) (19).
Para controlar la heterogeneidad primero se debe hacer una revisión de los datos y determinar si el MA se realizó de la forma correcta (17,19). Después se debe evaluar la causa de esta heterogeneidad realizando un análisis de subgrupos o una meta regresión (MR) entre otras (20). La MR es una extensión del MA tradicional que investiga básicamente la extensión en la cual la heterogeneidad estadística entre los estudio podría estar relacionada a una o más características del estudio (6).
Algunos autores consideran que el MA de estudios de intervención debería incluir solamente ensayos clínicos aleatorizados y controlados, ya que este tipo de estudios constituye un diseño más válido para la inferencia causal en comparación con el diseño observacional. Sin embargo, la revisión de los principales elementos que sustentan este concepto (que la aleatorización despeja la posibilidad de confusión, y que el doble-cegamiento minimiza el sesgo causado por el efecto placebo) sugiere que ambos tipos de diseño tienen fortalezas y debilidades, y que la inclusión de información a partir de estudios observacionales puede mejorar la inferencia basada solamente en ensayos clínicos aleatorizados. Más aún, una revisión de estudios empíricos sugiere que el MA basado en estudios observacionales produce una estimación de efecto similar a aquella proveniente del MA de ensayos clínicos aleatorizados. Las ventajas de incluir tanto estudios observacionales como estudios aleatorizados en un meta-análisis pueden superar a las desventajas en muchos casos, de manera que, los estudios observacionales no deben descartarse a priori (21). Así, la combinación de los resultados de ensayos clínicos (diseños experimentales) con los de estudios prospectivos de cohorte(s) (diseños observacionales) es un artificio al cual se recurre siempre que exista compatibilidad en los objetivos de estudio y siempre que cada diseño tenga la calidad suficiente para ingresarlo al análisis combinado. Esta tendencia epidemiológica actual es muy importante resaltarla, ya que la combinación de ambos diseños permite ganar información clave al respecto de los objetivos de estudio.
CONCLUSIONES
Este artículo nos permite tener una mayor comprensión sobre los fundamentos básicos del MA. Hay que tener en cuenta que esta revisión ha sido realizada de una manera amigable a través de gráficos tratando de tomar las principales definiciones que son pilares para la comprensión global de lo que es un MA, pero detrás de la metodología existe una amalgama de métodos matemáticos que no consideramos importantes para esta revisión. De esta forma entendemos cómo un MA se inicia luego de formular correctamente una pregunta de investigación, definir las variables, revisar sistemáticamente la literatura, y finalmente concluir en un resultado combinado a través de un análisis estadístico, teniendo en cuenta la evaluación de sesgo de publicación y heterogeneidad.
BIBLIOGRAFÍA
1. Evidence-Based Medicine Working Group. Evidence-based medicine. A new approach to teaching the practice of medicine. JAMA. 1992;268(17):2420-5. [ Links ]
2. Sackett DL, Rosenberg WM, Gray JA, Haynes RB, Richardson WS.
Evidence based medicine: what it is and what it isn’t. 1996. BMJ. 1996;312(7023):71-2. [ Links ]3. Blettner M, Sauerbrei W. [
Meta-analysis of epidemiologic studies]. Med Klin (Munich). 1998;93(7):442-5. [Article in German] [ Links ]4. Sacks HS, Berrier J, Reitman D, Ancona-Berk VA, Chalmers TC.
Meta-analyses of randomized controlled trials. N Engl J Med. 1987;316(8):450-5. [ Links ]5. Crowther M, Lim W, Crowther MA.
Systematic review and meta-analysis methodology. Blood. 2010;116(17):3140-6. [ Links ]6. Leandro G. Meta-analysis in Medical Research: The handbook for the understanding and practice of meta-analysis. Oxford: Blackwell Publishing, 2005. [ Links ]
7. Borenstein M, Hedges LV, Higgins JPT, Rothstein HR. Introduction to Meta-Analysis. United Kingdom: Wiley; 2009. [ Links ]
8. Bown MJ, Sutton AJ.
Quality control in systematic reviews and meta-analyses. Eur J Vasc Endovasc Surg. 2010;40(5):669-77. [ Links ]9. Guyatt GH, Oxman AD, Kunz R, Vist GE, Falck-Ytter Y, Schunemann HJ, et al.
What is “quality of evidence” and why is it important to clinicians? BMJ. 2008;336(7651):995-8. [ Links ]10. Dwan K, Gamble C, Williamson PR, Kirkham JJ; Reporting Bias Group.
Systematic review of the empirical evidence of publication bias and outcome reporting bias - an updated review. PloS One. 2013;8(7):e66844. [ Links ]11. Kicinski M.
Publication bias in recent meta-analyses. PloS One. 2013;8(11):e81823. [ Links ]12. Dickersin K.
The existence of publication bias and risk factors for its occurrence. JAMA. 1990;263(10):1385-9. [ Links ] 50 Rev Gastroenterol Peru. 2014;34(1):45-5113. Dwan K, Altman DG, Arnaiz JA, Bloom J, Chan AW, Cronin E, et al.
Systematic review of the empirical evidence of study publication bias and outcome reporting bias. PloS One. 2008;3(8):e3081. [ Links ]14. Egger M, Smith GD, Schneider M, Minder C.
Bias in meta-analysis detected by a simple, graphical test. BMJ. 1997;315(7109):629-34. [ Links ]15. van Driel ML, De Sutter A, De Maeseneer J, Christiaens T.
Searching for unpublished trials in Cochrane reviews may not be worth the effort. J Clin Epidemiol. 2009;62(8):838-44.e3. [ Links ]16. Sterne JA, Egger M.
Funnel plots for detecting bias in metaanalysis: guidelines on choice of axis. J Clin Epidemiol. 2001;54(10):1046-55. [ Links ]17. Hedges LV, Olkin I, Statistiker M, Olkin I, Olkin I. Statistical methods for meta-analysis. New York: Academic Press; 1985. [ Links ]
18. Blettner M, Sauerbrei W, Schlehofer B, Scheuchenpflug T, Friedenreich C.
Traditional reviews, meta-analyses and pooled analyses in epidemiology. Int J Epidemiol. 1999;28(1):1-9. [ Links ]19. Cooper H, Hedges LV, Valentine JC. Handbook of research synthesis and meta-analysis. New York: Russell Sage Foundation; 2009. [ Links ]
20. Higgins JP, Green S, Collaboration C. Cochrane handbook for systematic reviews of interventions: Wiley Online Library; 2008. [ Links ]
21. Shrier I, Boivin JF, Steele RJ, Platt RW, Furlan A, Kakuma R, et al.
Should meta-analyses of interventions include observational studies in addition to randomized controlled trials? A critical examination of underlying principles. Am J Epidemiol. 2007;166(10):1203-9. [ Links ] Todo el contenido de esta revista, excepto dónde está identificado, está bajo una Licencia Creative Commons
Todo el contenido de esta revista, excepto dónde está identificado, está bajo una Licencia Creative Commons













