Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO  uBio
uBio
Share
Revista de Investigaciones Veterinarias del Perú
Print version ISSN 1609-9117
Rev. investig. vet. Perú vol.26 no.2 Lima Apr. 2015
http://dx.doi.org/10.15381/rivep.v26i2.11095
http://dx.doi.org/10.15381/rivep.v26i2.11095
Una Aplicación del Muestreo de Gibbs en la Estimación de Parámetros Genéticos en Cuyes Utilizando MCMCglmm
An application of Gibbs sampling for genetic parameters estimation in guinea pigs using MCMCglmm
Ana Vargas P.1, Gustavo Gutiérrez R.2, Gerardo Mamani M.2
1 Departamento de Estadística e Informática, Universidad Nacional Agraria La Molina, Lima, Perú
2 Facultad de Zootecnia, Universidad Nacional Agraria La Molina, Lima, Perú
3 E-mail: anavargas@lamolina.edu.pe
RESUMEN
El objetivo de este estudio fue estimar parámetros genéticos para el peso al nacimiento y peso al destete en cuyes (Cavia porcellus) de una granja en Cieneguilla, Lima, Perú. Para el análisis se utilizó un modelo animal univariado que incluyó los factores sexo de la cría, número de parto, estación, animal y camada. Además, para el peso al nacimiento se incluyó como factor el total de nacidos y para el peso al destete se incluyeron como factores el número de nacidos vivos y la edad de la cría. Se estimaron los componentes de variancia utilizando el análisis bayesiano vía muestreo de Gibbs utilizando la librería MCMCglmm del software R. Se corrió una cadena de 100 000 iteraciones, de las cuales fueron descartadas las 10 000 primeras. El valor estimado de heredabilidad para el peso al nacimiento fue de 0.155 ± 0.036 y para el peso al destete fue de 0.246 ± 0.046, resultados similares a los reportados utilizando REML.
Palabras clave: heredabilidad, modelo animal, MCMCglmm
ABSTRACT
The aim of this study was to estimate genetic parameters for birth and weaning weight in guinea pigs (Cavia porcellus) reared in a farm in Cieneguilla, Lima, Peru. Univariate animal model that included sex of calf, parity, season of birth, animal and litter effect was used in the genetic analyses. In addition, the effect of number of newborns was included in the model for birth weight, and the number of born alive and age at weaning were included in the model for weaning weight. Variance components were estimated by Bayesian Gibbs sampling with a chain of 100 000 rounds with the first 10 000 rounds discarded for burn-in by using MCMCglmm library of R software. Heritability estimates for birth weight was 0.155 ± 0.036 and for weaning weight was 0.246 ± 0.046. These values were similar to those estimated by using REML.
Key words: heredability, animal model, MCMCglmm
INTRODUCCIÓN
La estimación de parámetros genéticos como la heredabilidad (proporción de la varianza fenotípica atribuida a factores genéticos aditivos) y correlación genética, los cuales son usados para predecir los valores de cría, son de gran interés en los programas de mejoramiento genético en animales. Los procedimientos estadísticos para realizar estas estimaciones se basan principalmente en dos grandes metodologías; una basada en máxima verosimilitud restringida, conocida como REML (Thompson, 2008), y otra basada en procedimientos bayesianos (Sorensen y Gianola, 2002).
Blasco (2001) señala que tanto la escuela frecuentista como la bayesiana están bien establecidas. Asimismo, se dispone de diversos programas de cómputo para analizar una gran variedad de problemas desde ambos puntos de vista. En general, los algoritmos para REML son más complicados de programar que los métodos vía muestreo de Gibbs (Misztal, 2008); sobre todo cuando los modelos son más complejos e involucran la estimación de varios parámetros y sus relaciones a partir de múltiples caracteres.
La metodología bayesiana está siendo aplicada en muchas áreas de interés en el mejoramiento genético animal. El trabajo de Wang et al. (1994) fue uno de los primeros en aplicar el análisis bayesiano vía muestreo de Gibbs, para estimar parámetros genéticos relacionados con el tamaño de la camada en cerdos ibéricos a partir de un modelo univariado. Ejemplos más recientes son los de Madureira et al. (2009), quienes estimaron el valor genético respecto al peso en bovinos utilizando metodología bayesiana a partir de modelos multicarácter, y los de Costa et al. (2009) y Cruz (2011), quienes aplicaron metodología bayesiana para la estimación de parámetros genéticos respecto al peso corporal en ganado de doble propósito y respecto al diámetro en la fibra de alpaca, respectivamente.
En cuyes, Solarte et al. (2002) y Cerón et al. (1998) reportaron valores de 0.12 y 0.27, respectivamente, para la heredabilidad respecto al peso al nacimiento, y de 0.13 y 0.24, respectivamente, para la heredabilidad del peso al destete, estimados a través de un modelo muticarácter bajo enfoque REML. Asimismo, Rodríguez (2013) estimó la heredabilidad del peso al nacimiento en 0.17 ± 0.05 y 0.26 ± 0.07 para la heredabilidad del peso al destete bajo el mismo enfoque. No se han encontrado trabajos que estimen parámetros genéticos en cuyes bajo un enfoque bayesiano.
El objetivo fue estimar la heredabilidad de las características peso al nacer y peso al destete en cuyes de una granja de la zona de Cieneguilla, Lima, a partir de modelos univariados utilizando métodos bayesianos implementados con la librería MCMCglmm del software R (R Core Team, 2013).
MATERIALES Y MÉTODOS
Se trabajó con datos existentes de cuyes (Cavia porcellus) mejorados sobre pesos al nacer y al destete (14 días en promedio) de 5120 crías en 1704 camadas, y de 117 progenitores machos y 868 progenitores hembras de la granja de cuyes de Cieneguilla de la Universidad Nacional Agraria La Molina, Lima, Perú. La información fue recolectada entre enero de 2009 y julio de 2011 (Rodríguez, 2013).
Según Sorensen y Gianola (2002) y Mrode (2014), el modelo animal univariado para datos de una variable fenotípica con distribución normal puede resumirse como:
y = Xß + Z1u1 + Z2u2 + ε, donde:
y es un vector que corresponde al peso al nacimiento o peso al destete;
ß es un vector que corresponde a los efectos del sexo de la cría, número de parto, estación y total de nacidos en el modelo que tiene como respuesta el peso al nacimiento, o a los efectos del sexo de la cría, número de parto, estación, nacidos vivos y edad de la cría en el modelo que tiene como respuesta el peso al destete;
u1 es el efecto genético aditivo del animal;
u2 es el efecto aleatorio de camada;
X, Z1 y Z2 son matrices de incidencia relacionadas con ß, u1 y u2, respectivamente; y
ε es el vector de error aleatorio.
La distribución condicional que generan los datos es:
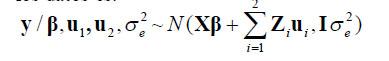
En los a priori para los componentes de varianza se asumió:
u1/A ~ N(0,As12), u2 ~ N(0, Is22) y ε ~ N(0, Ise2)
donde A es la matriz de covarianzas aditivas entre los individuos. Además, u1, u2 y ε son asumidas por ser independientes entre sí.
En los a priori para ß, como es usual, se asumió una distribución uniforme; es decir, p(ß)a constante, además de independencia entre ß, u1, u2 y ε.
Respecto a los a priori para las varianzas y covarianzas, se asumió una distribución inversa de Wishart; es decir, independientemente para cada componente de varianza corresponde una distribución gamma inversa parametrizada con dos parámetros.
La densidad posterior conjunta de todos los parámetros desconocidos es proporcional a:
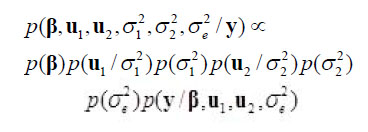
y a partir de estas se deducen las distribuciones posteriores completas de cada parámetro a estimar.
Para conseguir muestras de la distribución posterior conjunta, se aplicó el muestreo de Gibss con una sola cadena de 100 000 iteraciones y almacenadas cada 10 iteraciones, descartándose las 10 000 primeras (burn-in). Para ello se utilizó la librería MCMCglmm implementado en el paquete R (Hadfield, 2010).
Para estimar la heredabilidad del carácter en sentido estricto (Gutiérrez, 2010) se utilizó:
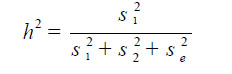
donde s12, s22 y se2 son la varianza aditiva, varianza respecto a la camada y varianza residual, respectivamente. Se asumió que las covarianzas entre los efectos aditivo, camada y residual fueron igual a cero.
RESULTADOS Y DISCUSIÓN
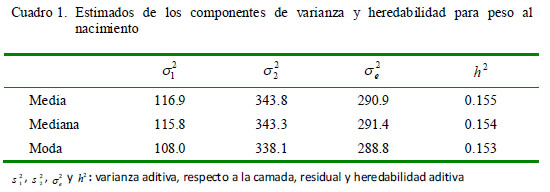
Los estimados de las medidas de centralidad (media, mediana y moda) de las distribuciones posteriores para los componentes de variancia y la heredabilidad para las características de peso al nacimiento y peso al destete se presentan en los Cuadros 1 y 2. Las estimaciones de las medias de la heredabilidad usando metodología bayesiana fueron de 0.155 ± 0.036 para el peso al nacimiento y 0.246 ± 0.046 para peso al destete. Las estimaciones de la heredabilidad, usando metodología REML, bajo modelos similares que la metodología bayesiana, fueron de 0.158 ± 0.037 y 0.245 ± 0.049 para el peso al nacimiento y peso al destete, respectivamente. Rodríguez (2013) consideró un modelo multicarácter para el peso al nacimiento y al destete y, utilizando REML, estimó la heredabilidad del peso al nacimiento en 0.170 ± 0.050 y del peso al destete en 0.260 ± 0.070, valores bastante similares a los obtenidos en el presente estudio.
Los resultados utilizando la metodología bayesiana y REML fueron similares, explicado por la coincidencia que existe entre los estimadores REML con la moda de la densidad posterior marginal conjunta de σ12, σ22 y σe2, cuando los valores priori son uniformes para ß y normales para los u1 y u2 (Blasco, 2001).
Los valores estimados pueden ser considerados bajos, indicando que la variabilidad fenotípica del peso al nacimiento y al destete se encuentran influenciados por factores diferentes a la acción aditiva, como el efecto genético materno y factores ambientales como la camada (Rodríguez, 2013). Sin embargo, Solarte et al. (2002), con un modelo también multicarácter, estimó valores ligeramente más bajos para la heredabilidad del peso al nacimiento (0.12 ± 0.05) y aproximadamente el 50% más bajo para la heredabilidad del peso al destete (0.13 ± 0.05) que los obtenidos en el presente estudio.
En el Cuadro 1 se puede observar que el componente de varianza que corresponde a la camada aporta aproximadamente el 46% de la variación total del peso al nacimiento y el 49% a la variación total del peso al destete, los cuales son más bajos en relación con las contribuciones obtenidas por Rodríguez et al. (2013) con 54 y 60% para el peso al nacimiento y peso al destete, respectivamente.
Además, estos autores encontraron contribuciones significativas de los componentes de varianza de las características en estudio, a través de modelos univariados para evaluar efectos de factores fijos y al azar.
El intervalo de credibilidad al 95% estimado para la heredabilidad del peso al nacimiento está entre 0.08 y 0.23, y para el peso al destete está entre 0.15 y 0.35, indicando que la heredabilidad es diferente de cero. Asimismo, indica que la heredabilidad del peso al destete es mayor que aquella del peso al nacimiento.
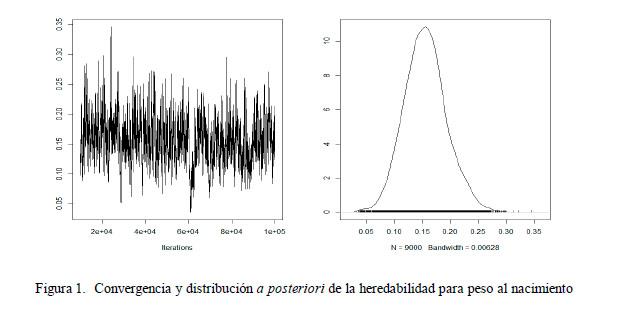
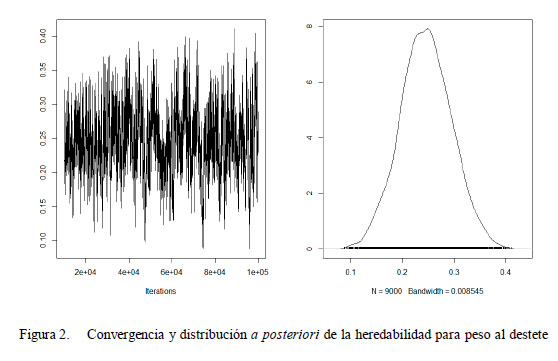
En las Figuras 1 y 2 se muestran las densidades marginales para las heredabilidades del peso al nacimiento y del peso al destete estimados de cada modelo; las cuales tienden a ser simétricas (media, mediana y moda son bastante cercanas), con un comportamiento prácticamente normal.
Las trazas (convergencia) muestran un comportamiento aparentemente aleatorio para los estimados de la distribución a posteriori de heredabilidad en cada uno de los caracteres; sin embargo, las correlaciones entre sucesivas muestras es alta (r>0.7), lo que podría indicar una débil convergencia de la cadena. Esto se refleja en el tamaño efectivo de la muestra no correlacionada que no es tan alta, tanto para la heredabilidad del peso al nacimiento como del peso al destete (Cuadro 3).
El error de Monte Carlo es bajo para las estimaciones de estos parámetros, pese a que no lo es para algunas estimaciones de componentes de varianza. Por otro lado, como el error de Monte Carlo está directamente relacionado con la inversa de la longitud de la cadena, este disminuirá cuando se aumente dicha longitud. En el presente estudio no se corrieron los modelos con mayores longitudes de cadena, puesto que los resultados fueron similares a los obtenidos por REML; además, las distribuciones posteriores de las características de interés mostraron ser bastante cercanas a la normal.
CONCLUSIONES
-
Las medias de los estimados de heredabilidad obtenidas vía muestreo de Gibbs en este trabajo fueron similares a los obtenidos vía REML, y a los obtenidos a estudios multicarácter con la misma información. Al compararla con estudios anteriores en cuyes, la heredabilidad estimada para el peso al destete fue algo mayor que con el peso al nacimiento aunque baja, por lo que se respalda la idea de que la variabilidad fenotípica de estas características están mayormente influenciadas por factores diferentes a la acción aditiva.
-
Podría recomendarse con fines explicativos y comparativos trabajar un modelo multicarácter desde una perspectiva bayesiana que permita además estimar la correlación genética entre ambas características, que en definitiva sería algo más cercano a la complejidad del problema y no solo de forma independiente.
Agradecimientos
Los autores agradecen al personal de la granja de cuyes de Cieneguilla de la Universidad Nacional Agraria La Molina por brindar las facilidades en la toma de datos.
LITERATURA CITADA
1. Blasco A. 2001. The Bayesian controversy in animal breeding. J Anim Sci 79: 2023-2046. [ Links ]
2. Cerón MF, Córdoba OA, Solarte CA, Delgado DE. 1998. Genetic and phenotypic parameters of some characteristics of economic importance in guinea pigs Cavia porcellus. En: 6th World Congress on Genetics Applied to Livestock Production. Armidale, NSW Australia. p 315-318. [ Links ]
3. Costa MTGP, Sanches A, Munari DP. 2009. Estimação bayesiana de parâmetros genéticos de pesos corporais em um rebanho da raça Guzerá. Nucleus Animalium 1(1): 1-13. doi: 10.3738/ na.v1i1.254 [ Links ]
4. Cruz LA. 2011. Estimación de parámetros genéticos para caracteres productivos en alpacas (Vicugna pacos), Perú 2011. Tesis de Magíster. Valencia, España: Univ Politécnica de Valencia. 66 p. [ Links ]
5. Gutierrez JP. 2010. Iniciación a la valoración genética animal. Metodología adaptada al EEES. UCM Ed Complutense. 355 p. [ Links ]
6. Hadûeld JD. 2010. MCMC Methods for Multi–response Generalized Linear Mixed Models: The MCMCglmm R Package. J Stat Software 33(2): 1-22. [ Links ]
7. Madureira AP, Oliveira HN, Rosa GJM, Bezerra LF, Marques LFA. 2009. Inferência bayesiana na predição de valores genéticos do peso aos 365 dias de bovinos de corte. Arch Zootec 58: 265-275. doi: 10.4321/S0004-05922009000200011 [ Links ]
8. Misztal I. 2008. Reliable computing in estimation of variance. J Anim Breed Genet 125: 363-370. doi: 10.1111/j.14390388.2008.00774.x [ Links ]
9. Mrode R. 2014. Linear model for the prediction of animal breeding value. 3rd ed. Edinburgh, UK: CABI. 343 p. [ Links ]
10. R Core Team. 2013. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. [Internet]. Disponible en: http://www.R-project.org/ [ Links ]
11. Rodríguez H, Palomino M, Hidalgo V, Gutiérrez G. 2013. Efectos de factores fijos y al azar sobre el peso al nacimiento y al destete de la costa central del Perú. Rev Inv Vet Perú, 24: 16-24. doi: 10.15381/rivep.v24i1.1647 [ Links ]
12. Rodríguez H. 2013. Evaluación fenotípica y estimación de parámetros genéticos en características productivas y reproductivas en cuyes de la granja de Cieneguilla. Tesis Doctoral. Lima: Univ Nacional Agraria La Molina. 79 p. [ Links ]
13. Solarte C, Imuez AM, Pérez T. 2002. Modelo animal multicarácter para la estimación de parámetros genéticos del Cavia porcellus en Colombia. Rev Cubana Cienc Agríc 36(1): 19-24. [ Links ]
14. Sorensen D, Gianola D. 2002. Likelihood, Bayesian and MCMC methods in quantitative genetics. New York, USA: Springer. 740 p. [ Links ]
15. Thompson R. 2008. Estimation of quantitative genetic parameters. P Roy Soc Lond B Bio 275: 679-686. [ Links ]
16. Wang CS, Rutledge JJ, Gianola D. 1994. Bayesian analysis of mixed linear models via Gibbs sampling with an application to litter size in Iberian pigs. Genet Sel Evol 26: 91-115. doi:10.1186/1297-9686-26-2-91 [ Links ]
Recibido: 20 de agosto de 2014
Aceptado para publicación: 25 de febrero de 2015