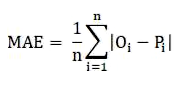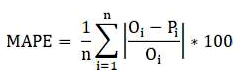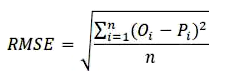INTRODUCCIÓN
Desde épocas ancestrales, los equinos han sido utilizados por el humano para el transporte y el trabajo; sin embargo, el equino también provee carne, pelo y cuero. En la actualidad, se estima que esta especie representa el 0.25% de la producción mundial de carne (Vanegas et al., 2016). Por otro lado, se tiene un creciente interés en la producción de leche equina por sus propiedades terapéuticas, conferidas por las altas concentraciones de lactoferrina, lisozima, ácidos grasos w3 y w6 (Uniacke-Lowe et al., 2010). La similitud en la composición entre la leche de la mujer y la leche de yegua hacen que esta última sea recomendada en la alimentación de neonatos prematuros y niños con alergia e intolerancia a la leche de vaca (Musaev et al., 2021).
La curva de lactancia en el mamífero representa el comportamiento de la producción de leche a través del tiempo (Noguera et al., 2011). Se dispone de valiosa información matemática de la curva de lactancia en vacunos; sin embargo, en equinos es limitada (Auclair-Ronzaud et al., 2022). Las características de la curva de lactancia están condicionadas por la especie, factores genéticos y ambientales (Quintero et al., 2007). La caracterización de las curvas de lactancia permite determinar la producción potencial de leche, la máxima producción de leche esperada (pico de producción) y la habilidad para mantener un rendimiento lechero relativamente constante durante la lactancia (persistencia) (Noguera et al., 2011). Esta información es útil para la gestión del criadero, permitiendo evidenciar el estatus sanitario y nutricional de la yegua y el potro, así como para la selección de animales por su habilidad materna y mayor producción de leche (Centoducati et al., 2012).
Diversos modelos matemáticos han sido propuestos para describir las curvas de lactancia en animales de interés zootécnico (Wood, 1967; Sikka, 1950; Singh y Gopal, 1982; Papajcsik y Bodero, 1988). Estos modelos pueden ser de tipo lineal o no lineal y estiman parámetros que buscan determinar la tasa de incremento en la producción láctea que ocurre después del parto, el punto de inflexión de la curva que se corresponde con el pico de producción y la tasa de descenso observado en la producción de leche que ocurre después de que los animales alcanzan el pico de producción. El objetivo de este trabajo fue comparar seis modelos matemáticos para describir la curva de lactancia en yeguas.
MATERIALES Y MÉTODOS
Se evaluaron seis modelos matemáticos frecuentemente empleados para describir la curva de lactancia en vacas lecheras.
El primer modelo correspondió a la función gamma incompleta propuesta por Wood (1967) (Modelo Wood): Y =an b exp(-c n), donde Y representa la producción de leche en el día n de lactancia y a, b y c son parámetros del modelo. Este modelo predice el pico de producción de leche (litros) como a(b/c) b , el cual ocurre a los b/c días después del parto.
Papajcsik y Bodero (1988) proponen una versión modificada del modelo propuesto por Wood (1967) (Wood modificado): Y=an exp (-c n). El modelo Wood modificado estima los litros de producción de leche al pico como a/c*0.3678 alcanzada en el tiempo 1/c.
Sikka (1950) propuso un modelo exponencial parabólico para describir la curva de lactancia (Modelo Sikka): Y= a exp(b n -c n 2 ). Este modelo se asemeja a la curva normal usada en estadística y el tiempo (días) y la producción al pico (litros) se estiman a través de las expresiones b/(2c) y a*exp((b (b-c))/ 2c) 1/2 , respectivamente.
Dave (1971) modelando la producción de leche en búfalos, propone un modelo cuadrático para ajustar las curvas de lactancia (Modelo cuadrático): Y=a+bn -c n 2 ). Este modelo carece de punto de inflexión; por tanto, el parámetro a, corresponde a la máxima producción de leche (litros) alcanzada en el tiempo -b/ 2c (días).
Singh y Gopal (1982) relatan el uso de un modelo lineal acumulativo logarítmico «linear-cum-log» para modelar curvas de lactancia en búfalos (Modelo Singh-Gopal): Y=a-bn+cln (n). El modelo no está definido para el tiempo n =0y predice que el pico de producción de leche ocurre a los c/b días después del parto.
El último modelo bajo evaluación fue el propuesto por Cobby y Le Du (1978). Se trata de un modelo exponencial con una disminución lineal después del punto de inflexión (Modelo Cobby): Y=a-bn+a exp (-c n). Este modelo predice que el pico de producción de leche ocurre a los c -1 ln(ac/b) días después del parto.
La base de datos empleada para la modelación corresponde a la reconstrucción por interpolación gráfica de 197 registros de producción de leche de yeguas lactantes entre los 2 y 190 días de lactancia reportados por Coenen et al. (2011). Los datos analizados tienen una media de producción de leche de 10.05 ± 4.2 L y valores mínimos y máximos de 1.99 y 28.81 L. respectivamente. Los modelos fueron ajustados empleando algoritmos de regresión no lineal dispuestos en la librería ‘stats’ de R Core Team (2022). El desempeño de los modelos fue evaluado empleando los siguientes criterios de comparación descritos por Rosero-Noguera et al. (2022) y Posada y Rosero (2007):
Error absoluto medio (MAE):
Error porcentual absoluto medio (MAPE):
Raíz del error cuadrático medio (RMSE):
donde Oi, Pi y n corresponden a los valores observados, valores predichos por el modelo y el número de observaciones, respectivamente.
Criterio de información de Akaike (AIC): AIC = -2 log lik + 2k; Criterio de información bayesiano (BIC): BIC = 2 log lik + log(m) k, donde log lik corresponde al logaritmo de máxima verosimilitud, k al número de parámetros del modelo y m es el número de observaciones.
Los residuales definidos como la diferencia entre los valores observados y predichos por el modelo fueron analizados para determinar normalidad de residuales, constancia de la varianza del error, independencia entre residuales y ausencia de datos extremos (outliers). La normalidad de residuales se evaluó a través de la prueba de Shapiro-Wilk (p<0.01), la constancia en la varianza del error se determinó graficando los residuales frente a los valores estimados por los modelos, buscando determinar si la magnitud del sesgo aumentó o disminuyó con la magnitud de los valores estimados. La correlación entre residuales es una medida de la independencia de los términos del error y fue estudiada graficando los residuales del tiempo (ti) contra aquellos del tiempo precedente (ti -1). Para determinar la ausencia de outliers se graficaron los residuales estandarizados frente al tiempo (Posada y Rosero, 2007). Se consideraron valores outliers aquellos puntos a dos o más desviaciones estándar del punto cero.
RESULTADOS Y DISCUSIÓN
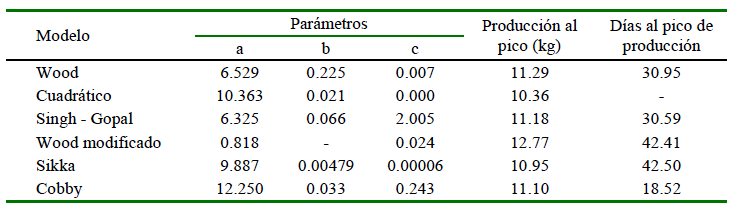
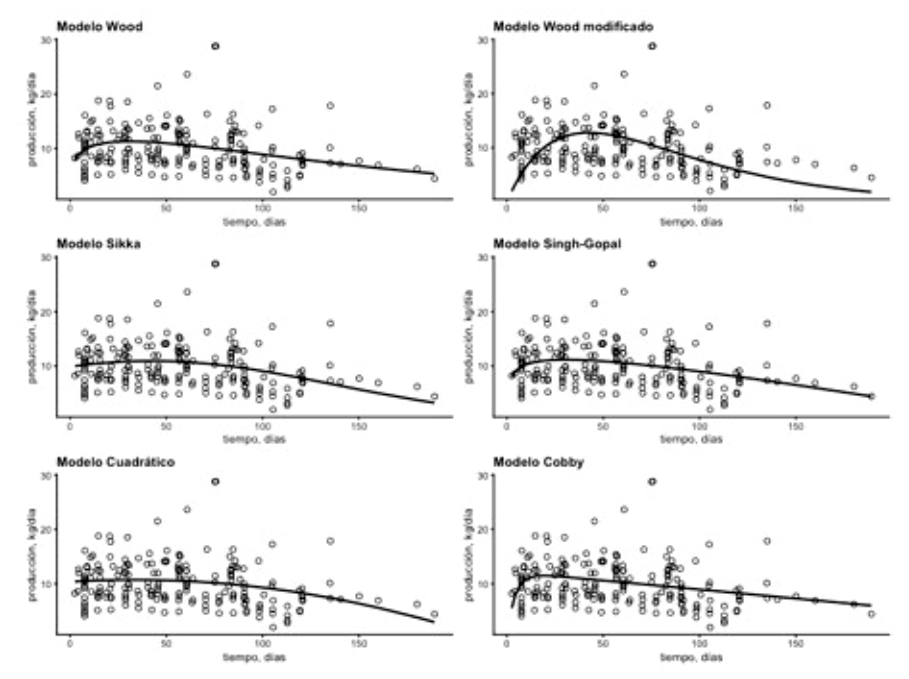
Los parámetros de ajuste para los modelos evaluados se describen en el Cuadro 1. En términos generales, los modelos predicen que la máxima producción de leche (pico de producción) esperada varía entre 10 y 13 kg, la cual ocurre entre los 18 y 43 días posparto. A excepción del modelo Cuadrático, todos los modelos permitieron estimar el tiempo requerido para que los animales alcancen el pico de producción de leche. En el caso de los modelos Singh-Gopal y Wood, el pico de producción de leche se presentan alrededor de los 30 días posparto, para los modelos Wood modificado y Sikka ocurre a los 42 días, mientras que para el modelo Cobby se presentaría alrededor de los 18 días posparto.
Según Miraglia et al. (2020), el volumen de producción de leche en yeguas reportado por la literatura varia ampliamente, debido principalmente a las metodologías empleadas para determinar la producción de leche, entre ellas el ordeño directo, peso del potro antes y después del amamantamiento y el empleo de isotopos radiactivos (deuterio y tritio) (Auclair-Ronzaud et al., 2022). Datos recopilados de la literatura reportan producciones diarias de leche 11.7 kg/día, con valores mínimos y máximos de 3.9 y 17.2 kg/día, respectivamente (De Palo et al., 2016; Iskhan et al., 2019; Akimbekov et al., 2017).
Centoducati et al. (2012), ajustando el modelo Wood a las curvas de lactancia de yeguas de tiro pesado encontraron que el pico de producción de leche ocurrió a los 69 días, con una producción de 17.01 kg/día. Santos y Silvestre (2008) modelaron la curva de lactancia de yeguas Lucitano reportando producciones máximas de 14 kg/día a los 31 días de lactancia. Doreau et al. (1990) empleando isótopos radiactivos encontraron incrementos en la producción de leche hasta los dos meses después del parto. En este estudio, cuatro de los modelos evaluados predijeron que la máxima producción de leche ocurrió entre los 30 a 42 días posparto.
La Figura 1 muestra el ajuste de los modelos evaluados a los datos observados de producción de leche. Claramente puede verificarse que las curvas de los modelos Wood, Wood modificado, Sikka, Singh-Gopal y Cobby presentan un punto de inflexión de la curva que es asociado al pico de producción de leche. El modelo Cuadrático carece de este punto de inflexión indicando que la máxima producción de leche ocurre al inicio de la lactancia.
Diferentes criterios de comparación entre modelos fueron establecidos (Cuadro 2). En el caso del MAE el error es calculado como el promedio de la diferencia entre los valores observados y predichos sin considerar su signo, de allí que, a menor valor, mejor será el ajuste del modelo. En este estudio el valor del MAE fue menor para los modelos Wood (3.07) y Singh-Gopal (3.08), mientras que los modelos Cuadrático y Sikka y Cobby presentaron un valor de 3.11 y el modelo Wood modificado un valor de 3.47.
Cuadro 2. Criterios de comparación de modelos
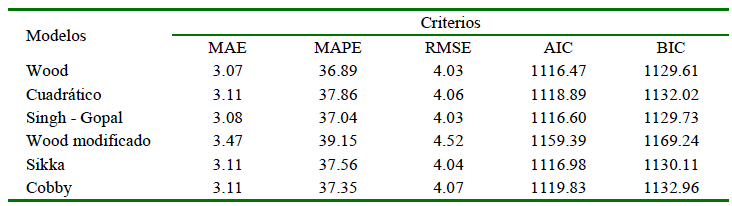
MAE: Error absoluto medio; MAPE: Error porcentual absoluto medio; RMSE: Raíz del error cuadrático medio; AIC: Criterio de información de Akaike; BIC: Criterio de información bayesiano.
Los valores de MAE fueron muy próximos entre los modelos (promedio: 3.16), valor que indica que la predicción realizada por los modelos se aleja de los valores observados en 3.16 kg de leche, que porcentualmente corresponde a 37.6% (promedio de los valores de MAPE). En este trabajo los valores de MAPE variaron entre el 36.9 y 39.2% (Cuadro 2). DeLurgio (1997) propone los siguientes criterios para interpretar los valores de MAPE: <10% corresponden a modelos de alta precisión de predicción, 10-20% se asocian con modelos de buena capacidad de predicción, 20-50% con razonable capacidad de predicción y >50% con limitada capacidad de predicción. De acuerdo con esta clasificación, los modelos evaluados presentaron una razonable capacidad de predicción.
El RMSE determina la desviación estándar de los valores residuales. Un mejor ajuste del modelo es indicativo de un menor valor de este criterio. En el presente estudio, los menores valores de RMSE se determinaron en los modelos Wood (4.03) y Singh-Gopal y Sikka (4.04) y el mayor valor correspondió al modelo Wood modificado (4.52). En valor promedio de RMSE fue 4.13, lo que significa que los valores predichos se alejan de los valores observados en ± 4.13 kg de leche.
Los criterios AIC y BIC son ampliamente utilizados para determinar la capacidad de ajuste de los modelos matemáticos. Cuanto menor sea el valor de estos criterios, mejor será el ajuste del modelo y mayor su exactitud de predicción. El menor AIC y BIC fue registrado para los modelos Wood y Sikka (Cuadro 2).
En el presente estudio se tomaron en consideración diversos criterios de evaluación de modelos, dejando de lado una de las métricas de más amplia utilización para determinar la bondad de ajuste de los modelos; es decir, el coeficiente de determinación (R2). Esta métrica es completamente válida para modelos lineales, pero inválida para modelos no lineales una vez que, para estos últimos, la suma de cuadrados de la regresión (SSR) + la suma de cuadrados del error (SSE) no es igual a la suma de cuadrados total (SST). Spiess y Neumeyer (2010) demostraron que emplear el R2 como criterio de comparación de modelos no lineales solo permite seleccionar los mejores modelos entre 28 y 43% de las veces. Estos mismos autores proponen emplear criterios alternativos como el AIC y el BIC.
Los criterios de evaluación de modelos empleados en este estudio presentaron valores muy próximos entre sí. Todos los modelos mostraron buena capacidad de ajuste (Cuadro 2); sin embargo, los modelos Wood, Singh-Gopal y Sikka presentaron los menores valores de MAE, MAPE, RMSE, AIC y BIC, razón por la cual se sugieren como adecuados para modelar curvas de lactancia en équidos.
A través de la prueba de Shapiro-Wilk pudo establecerse que los valores residuales en los seis modelos evaluados no siguen una distribución normal (Cuadro 3). La normalidad de residuales es importante puesto que los intervalos de predicción se calculan bajo la premisa de normalidad. Si los residuos no son normales, los intervalos de predicción pueden ser inexactos. De acuerdo con Coock y Weisberg (1982), la normalidad de residuales en modelos predictivos se torna más importante cuando el número de observaciones para construir el modelo es inferior a 15. Modelos construidos con tamaños muestrales superiores proporcionan predicciones confiables para cualquiera de las distribuciones no normales.
Cuadro 3. Test de normalidad Shapiro-Wilk (W) para seis modelos matemáticos de predicción de curvas de lactación de yeguas
| Modelo | W | p-valor |
|---|---|---|
| Wood | 0.91 | 0.01 |
| Cuadrático | 0.92 | 0.01 |
| Singh -Gopal | 0.92 | 0.01 |
| Wood modificado | 0.96 | 0.01 |
| Sikka | 0.92 | 0.01 |
| Cobby | 0.92 | 0.01 |
Para determinar la constancia en la varianza del error, los valores residuales fueron graficados frente a los valores predichos por los modelos (Figura 2). Pudo verificarse que los residuales se distribuyen a uno y otro lado del valor cero, sin que se pueda observar un patrón lineal entre ellos. En esta misma figura, puede observarse que los modelos Wood, Sikka, Singh-Gopal y Cuadrático claramente tienden a subestimar la producción de leche al inicio de la lactancia. Por su parte, el modelo Wood modificado realiza mejores predicciones de las etapas iniciales de la lactancia. La ausencia de un patrón en la distribución de residuales es un indicativo de homocedasticidad (Figura 3).
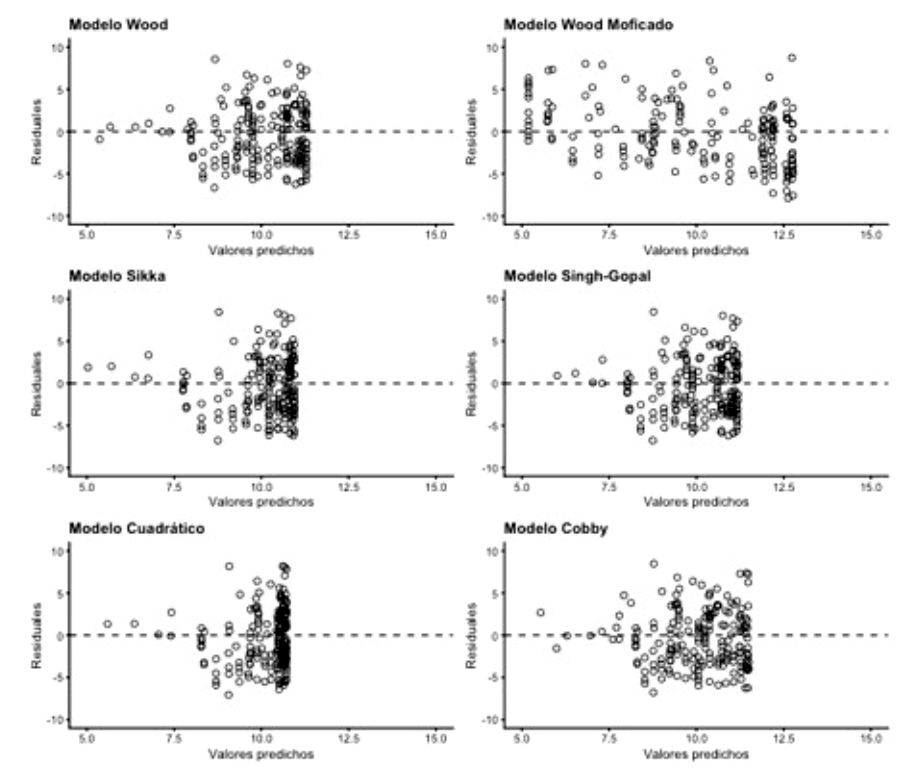
Figura 2. Análisis de dispersión de residuales para la curva de producción de leche de yeguas ajustada por los modelos Wood, Sikka, Cuadrático, Wood modificado, Singh-Gopal y Cobby
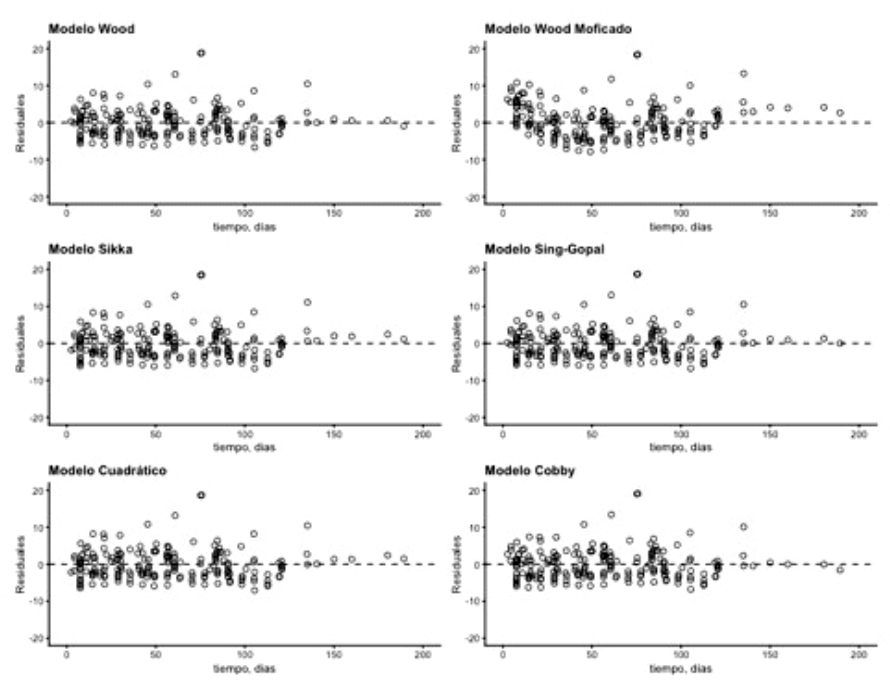
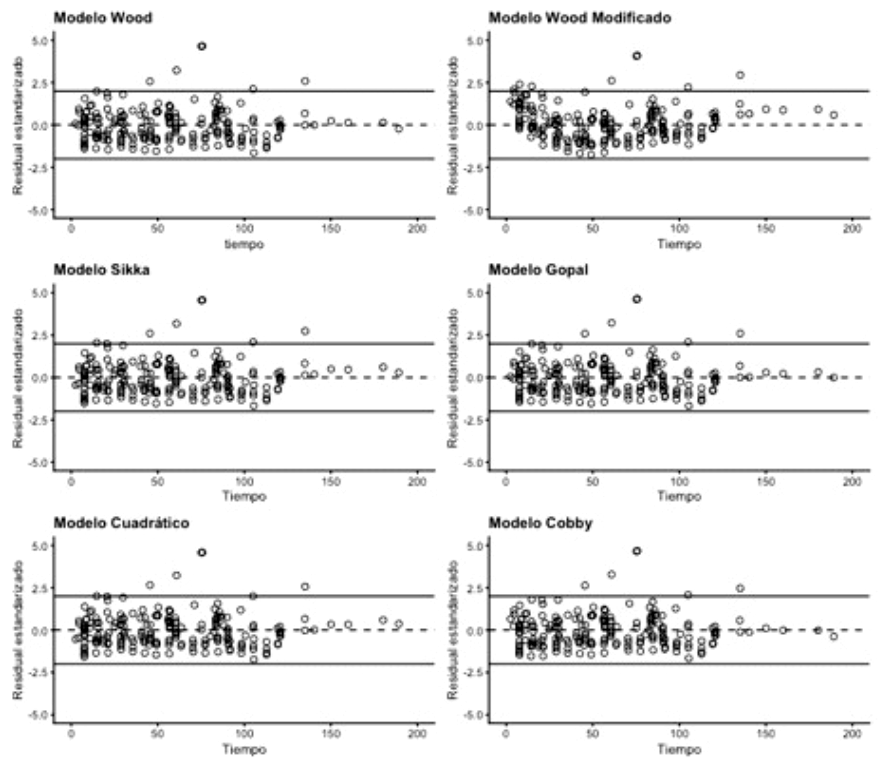
Figura 3. Distribución de los residuales a través del tiempo de los modelos Wood, Sikka, Cuadrático, Wood modificado, Singh-Gopal y Cobby, empleados para modelar la curva de lactancia en yeguas
Los residuales representan la variación que no puede ser explicada por el modelo. Si los residuales son aleatorios podemos suponer que representan un ruido aleatorio en el sistema. Si no son aleatorios, la implicación es que el modelo no explica alguna estructura en los datos, haciendo necesario incluir un parámetro adicional o una nueva variable al modelo.
La independencia entre residuales (ausencia de correlación) se determinó graficando la relación entre el residual actual (ti) y el precedente (ti-1) (Figura 4). Los puntos ubicados en los cuadrantes I y III indican que un residual positivo fue precedido por un residual negativo o viceversa, lo que sugiere ausencia de correlación serial. Residuales del mismo signo estarían indicando que el modelo sobre o subestima algunas secciones de la curva de lactancia. En general, todos los modelos registraron puntos ubicados en los cuadrantes I y III, lo que sugiere autocorrelación serial. Idealmente, la nube de puntos debería ubicarse lo más cerca posible del punto de coordenadas (0, 0) lo que sería un indicativo de residuales pequeños y mayor capacidad de predicción del modelo. En este estudio, los modelos evaluados tuvieron equiparable capacidad de predicción, razón por la cual determinar gráficamente que modelo presenta la mayor capacidad de predicción es difícil.
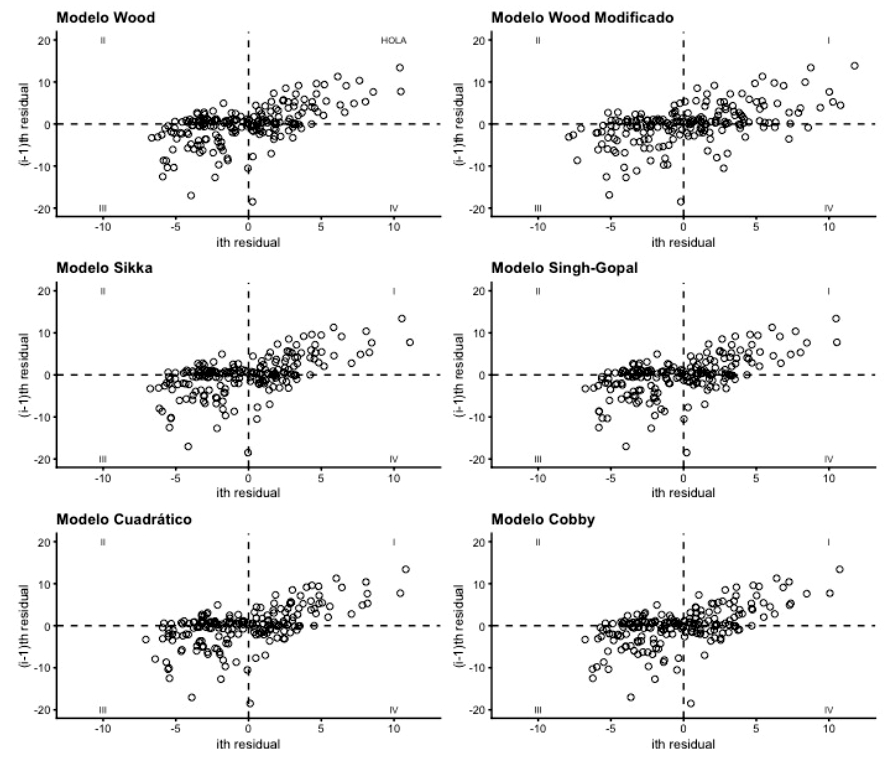
Figura 4. Relación entre el residual actual y precedente para los modelos Wood, Sikka, Cuadrático, Wood modificado, Singh-Gopal y Cobby en la predicción de la producción de leche de yeguas
Los valores atípicos (outliers) en la base de datos fueron determinados gráficamente (Figura 5). Se consideraron valores atípicos aquellos puntos a dos o más desviaciones estándar del punto cero. En la base de datos, solo cinco datos se alejaron a más de dos desviaciones estándar del punto cero. Por definición, un valor atípico es aquella observación que numéricamente es muy distinta del resto de los elementos de la base de datos. Los valores atípicos pueden deberse a errores asociados al proceso de medición, muestreo y determinación. De acuerdo con Kwak y Kim (2017), los datos atípicos son un indicativo de aleatoriedad de la variable de estudio y recomiendan varias alternativas para su manejo en el análisis de datos: eliminar el dato atípico, remplazar el valor del valor atípico y reducir la influencia de los valores atípicos mediante ajustes de peso de los valores atípicos.
CONCLUSIONES
Los criterios de comparación de modelos muestran que los modelos Singh-Gopal y Wood presentan una ligera superioridad para describir la curva de lactancia en yeguas, prediciendo una producción máxima de leche de 11.2 y 11.3 kg/día, respectivamente, a los 30.6 y 30.9 días, correspondientemente.
Los residuales de todos los modelos evaluados no se distribuyeron de forma normal, posiblemente porque el número de observaciones al inicio y al final de la lactancia en la base de datos es pequeño.












 uBio
uBio