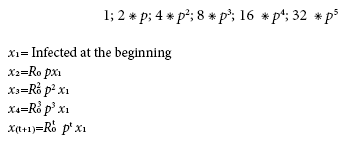Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Peruana de Medicina Experimental y Salud Publica
versión impresa ISSN 1726-4634
Rev. perú. med. exp. salud publica vol.37 no.2 Lima abr./jun 2020
http://dx.doi.org/10.17843/rpmesp.2020.372.5405
Original article
Estimated conditions to control the COVID-19 pandemic in peruvian pre- and post-quarantine scenarios
1 Hospital Nacional Adolfo Guevara Velasco, Cusco, Perú.
2 Universidad Andina del Cusco, Cusco, Perú.
3 Instituto de Evaluación de Tecnologías en Salud e Investigación, EsSalud, Lima, Perú.
INTRODUCTION
Controlling an epidemic depends, among other factors, on the current knowledge about the disease and how this information is used in decision-making. Therefore, knowing the contagion periods, the number of people susceptible, the spread speed, among others, is necessary to predict the progression of the disease. The problem with the coronavirus disease (COVID-19) pandemic is that such new information is being generated constantly and decisions are based on highly uncertain assumptions 1.
Once the epidemic in China was first reported, preventive measures took several weeks to be stablished worldwide. In Peru, social distancing was implemented once the first cases were detected 2. Other mitigation measures followed, but due to their low effectiveness, the Government was forced to decree national quarantine on March 16, 2020. These measures (mitigation and suppression strategies) were possibly implemented based on the recommendation of experts who generated mathematical models to simulate the impact of the epidemic 3. However, when the national quarantine was decreed, some local groups rejected the idea.
Mitigation and suppression measures proposed by the Government of Peru required citizen participation; nonetheless, there have been societal difficulties in complying with these. Other measures directed towards the health sector included increasing the number of hospital beds and health personnel, as well as the timely detection of people with COVID-19. Early diagnosis is intended to promote isolation in order to cut off the spread of disease and carry out contact tracing. Our study aims to determine the probability of controlling the COVID-19 outbreak in Peru, in a pre- and post-quarantine scenario with mathematical simulation models, and without the effect of social mitigation measures. Considering only the isolation of positive cases and the tracing of their contacts, in scenarios with greater or lesser supply of beds in intensive care units (ICU).
KEY MESSAGES
Motivation for the study: Mathematical modeling at the beginning of the COVID-19 pandemic was carried out to estimate the number of cases, but not the conditions for starting or suspending quarantine.
Main findings: The COVID-19 pandemic would only have been controlled if all patients were detected and isolated from the start. To be successful in controlling the post-quarantine pandemic, the spread of the virus must be significantly reduced, all cases must continue to be isolated, and the percentage of contacts traced must be close to 100%.
Implications: Control of the pandemic is not possible without slowing the spread of the disease. This is a matter of a societal nature. In the health sector, it is necessary to identify all cases, isolate them and trace their contacts. Scenarios with less active participation have a high probability of failure.
MATERIALS AND METHODS
The Centre for Mathematical Modelling of Infectious Diseases at the London School of Hygiene & Tropical Medicine 4 designed a model available for free download in the Rproject software, based on the disease assumptions known up to 5 February 2020 (Table 1).
Table 1 Assumptions used in mathematical modeling
| Concept | Values | Reference |
|---|---|---|
| Patients with subclinical infection | 18% and 40% | Mizumoto 9 , Nishiura 10 |
| Incubation time (days) | 5.8 ± 2.6 | Li 11 |
| Isolation time (days) | ||
| Early | 3.43 (2.02-5.23) | Donnelly 12 |
| Late | 8.09 (5.52-10.93) | Hellewell ( 4 |
| R0 | ||
| Pre-quarantine | 2.7 and 3.5 | Liu 7 , Chen 6 |
| Post-quarantine | 1.5, 2.0 and 2.7 | |
| Number of ICU beds | 50 or 150 | Assumed |
| Initial number of cases | ||
| Pre-quarantine | 1, 5 or 10 | Assumed |
| Post-quarantine | 20, 40 or 60 |
R0: basic reproductive number; ICU: intensive care unit
Stochastic differential equations
The study designed by Hellewel et al. 4 was based on a mathematical model which originated from stochastic differential equations, and has the following modeling concepts.
If x(t) is the number of infected persons in a day, the equation in linear stochastic difference associated with x(t) is described in Figure 1, where p+q=1. When in contact with an infected person; p represents the probability of a person becoming infected, while q is the probability of not becoming infected.
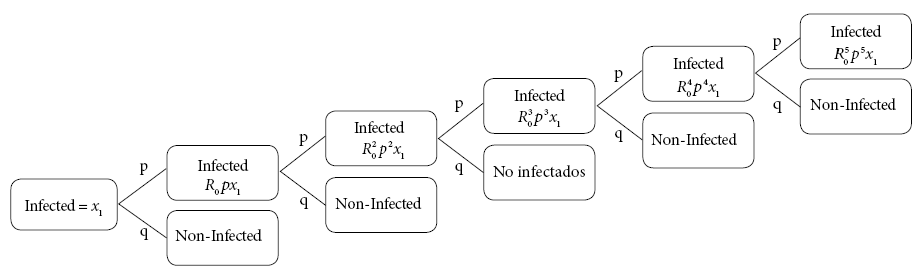
Figure 1 Disease spread according to the probabilities established in the stochastic difference equation model
This is one way of explaining the speed of the virus’ spread which is usually done using the R0 (basic reproductive number). That being said, the sequence for the number of new infections per day would be:
Infected at the beginning
Among other variables, the R0 varies according to the disease, the mechanism of contagion, and the population interaction 5. There are several R0 estimates for the COVID-19 epidemic, some studies indicate that it varies from 3.5 in person-to-person contact, or 2.5 in person-to-reservoir/fomite contact 6. R0 variability ranges from 1.4 to 6.5 (7.8), with a median of 2.7. When this study concluded, a Peruvian R0 was not yet available neither for the pre-quarantine or quarantine stage.
Assumptions for mathematical modeling
The study by Hellewell et al. 4 used the following assumptions for its mathematical modeling: 1) if a positive case was detected, it was sent into early isolation for 3.43 days; 2) the incubation period of the disease was 5.8 days; 3) the R0 was 2.5 in the community and 0 in isolation; 4) the percentage of subclinical infected cases was 0%; and 5) most importantly, they defined success in controlling an outbreak if the spread did not exceed 5,000 cases. These assumptions were tested in scenarios where positive case isolation measures were initiated after 5, 10 or 20 cases had been detected.
We updated the disease behavior data according to the new information available. While the spread of the disease and the response of the health system are variables. In Peru we do not have any data on this matter, so we carried out the modeling based on the following assumptions:
Pre-quarantine scenario: In which the R0 would be 2.7 and 3.5. The R0 of 2.7 corresponds to the median of the R0 values calculated from 12 studies 7. Nonetheless, a second R0 of 3.5 was posed ( 6, which would correspond to an adverse scenario. In this adverse scenario, the positive case isolation measures and the contact follow-up, are assumed to begin with 1, 5 or 10 cases. Higher values for R0 are not assumed, due to the fact that in such models, control of the outbreak would be unsustainable.
Post-quarantine scenario: A scenario where the R0 could be 1.5, 2.0 or 2.7. Starts with a R0 value of 1.5 because it would be the best-case scenario after quarantine (assuming that the learned and reinforced behaviors in quarantine will diminish the interaction with the decrease in the spread dynamic). Another modeling with a R0 of 2.7 was made, which would be the starting scenario with no learning from the pandemic. In the latter modelling it is assumed that the quarantine is lifted when 20, 40 or 60 cases are registered per day.
The percentage of patients with subclinical infection was modified in both scenarios, the current being 18 9. This information originates from what happened at the Diamond Princess Cruise, which was kept quarantined and tested every passenger. In a real scenario, the subclinical or asymptomatic infected cases would not be tracked, and could continue to spread the disease. On the other hand, symptomatic cases would spread the disease until being isolated. A second analysis is carried out, with 40% asymptomatic cases 10, which corresponds to a pretty bad asymptomatic infection scenario.
The incubation time estimates for the disease (5,8 ± 2,6 days) were maintained 11, as well as the fact that 15% of the contagion occurred before the symptom onset, and the assumption that isolation decreases the R0 to 0.
The duration of the time to isolation was chosen based on findings from the severe acute respiratory syndrome (SARS-CoV) pandemic and from the initial stage of the COVID-19 pandemic, both of these measures were used in the original study. The time to isolation in the SARS-CoV 2003 outbreak was of 3.43 days (2.02-5.23) 12 and it is referred to as “early isolation”. During the initial stage of the COVID-19 pandemic the time to isolation was of 8.09 days (5.52-10.93) 4 and is referred to as “late isolation”. Given that the first case in Peru was isolated 10 days after being reported, baseline calculations are made considering “late isolation”. In the post-quarantine analysis, “early isolation” is considered, as it is assumed that the epidemiological surveillance and control measures were improved, thus reducing the delay.
Finally, “outbreak control” was defined as the absence of new infections from 12 to 16 weeks after detecting the initial cases. The original study assumed that outbreaks reaching over 5,000 cumulative cases were too large to be controlled. However, this European assumption does not reflect the case-resolving capacity of Peru, where there are a limited number of ICU beds for management of patients with COVID-19.
The original study based the outbreak control on the maximum number of cases detected, we made the modeling considering the maximum number of beds in the ICU required, in scenarios where there are 50 or 150 beds in the pre-quarantine stage, and 150 beds in the post-quarantine stage. The modeling with 50 beds is done to try to reflect what could happen in provinces or cities other than Lima, with less case-resolving capacity.
RESULTS
Pre-quarantine scenario
Two scenarios are proposed according to the propagation dynamics, considering that the basal R0 is of 2.7 and the unfavorable R0 is of 3.5 (Figure 2).
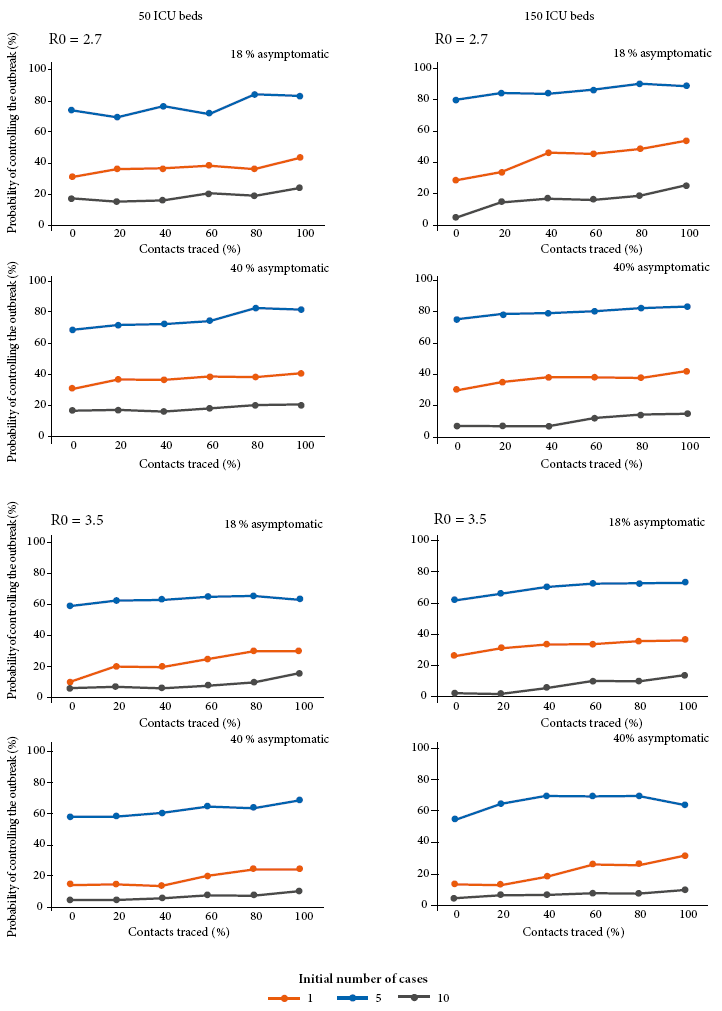
Figure 2 Probability of controlling simulated outbreaks according to different numbers of initial cases, different propagation scenarios (R0) and with different proportions of asymptomatic cases. The R0 used represents an ordinary (R0=2.7) or unfavorable (R0=3.5) scenario for Peru. Both scenarios are performed considering late isolation for positive cases (average 8.1 days), and 15% transmission before the onset of symptoms.
In the baseline scenario, if measures are implemented from the first case onward, the probability of success in controlling the outbreak is close to 80%, even without the need for contact tracing. If isolation measures are implemented when there are already 5 cases detected, 100% of the contacts should be traced to obtain a success rate of 40%. Implementing measures when there are more than 10 cases detected, in all scenarios, shows a probability of success in controlling the outbreak of less than 20%. The effect from the asymptomatic people percentage barely changes the outbreak control scenarios when measures are implemented from the first case detected.
In the worst-case scenario (R0=3.5), if measures are implemented from the first case onward, isolation measures by themselves would be enough to obtain a success rate of at least 60% in controlling the outbreak. Contact tracing increases the probability of success in controlling the outbreak up to 80%. But, if isolation measures are implemented when there are 5 or 10 cases detected, success rate decreases to less than 40%, even when tracing 100% of the contacts.
Post-quarantine scenario
It is assumed that when quarantine ends the R0 decreases to 1.5, 2 or 2.7 in the worst-case scenario, furthermore, the assumption of “late isolation” could be updated and changed to “early isolation”.
From all of the scenarios shown in Figure 3, the one with a success rate of 80% is the one that integrates early isolation of positive cases, 100% of contacts traced, and a R0 of 1.5; regardless if the quarantine ends with 20, 40 or 60 cases (Figure 3).
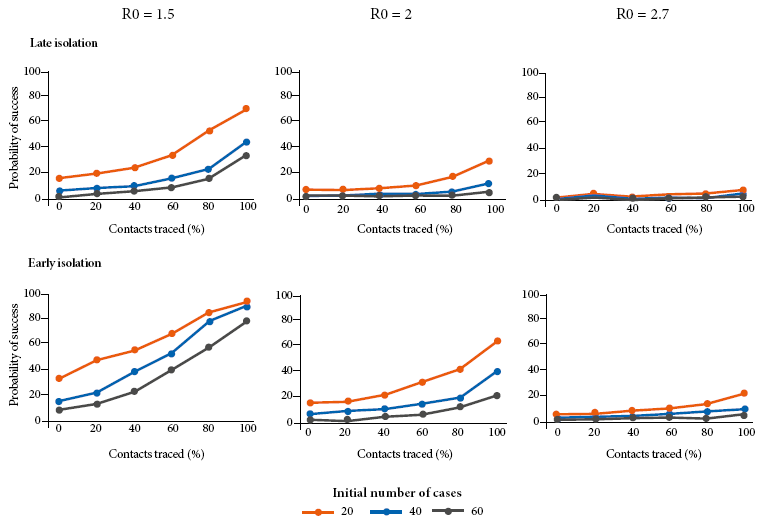
Figure 3 Probability of success in controlling the outbreak in different scenarios, starting with 20, 40 or 60 cases. In this differentiated propagation scenarios (R0), the percentage of asymptomatic people is 18%. It is differentiated according to early (average 3.4 days) or late isolation (average 8.1 days)
In a more conservative scenario, where the R0 decreases to 2, quarantine could end with 20 positive cases; but 100% of contacts traced should be guaranteed to obtain approximately a success rate of 60% in controlling the outbreak.
If early isolation of positive patients is not yet achieved, there would still be a 60% chance of success in controlling the outbreak if the R0 decreases to 1.5 and quarantine ends with 20 positive cases and 100% of contacts traced.
DISCUSSION
Public health decisions are recommended to be based on evidence and to have technical support. At the onset of the COVID-19 pandemic, information was either absent or uncertain 1, so several initiatives emerged to provide epidemiological and clinical information to help make better decisions. In this studies, mathematical modeling was used to simulate scenarios that predict the pandemic development to be able to make decisions ahead of time 13 14. We decided to show part of a scenario that is still under development. This scenario evaluates, in an isolated way, the effectiveness of epidemiological surveillance by identifying cases, isolating them and tracing their contacts. All of this depends on the health system logistics, so these would be scenarios where social participation would only be reflected in the R0 variation.
In Peru, although the first positive case was isolated and the contacts were traced, the process of identification and isolation of the case was late. In the ideal scenario of “early isolation” from the first positive case, a low percentage of contacts traced would have been required. But that ideal scenario would have involved a more rigorous migration control from the beginning and having the correct control of all possible suspects and their subsequent follow-up. Changing the scenario to five cases to implement the isolation or tracing of cases can be interpreted as if the detection measures were surpassed and five cases went undiagnosed, in this scenario the probability of controlling the outbreak would be less than 40%. Perhaps that is why countries such as Russia and South Korea, both of which took very quick but different decisions, such as closing borders or strictly monitoring confirmed and suspected cases 15 16, have had better results in controlling the pandemic.
European models about propagation dynamics represented by the R0 could not be applied to Peru, because it has greater social interaction and low healthcare case-resolving capacity. This is why a greater number of cases for a reduced supply of ICU beds is expected, therefore, the main objective would be to minimize the number of cases that require mechanical ventilation 17. Taking action with only a few cases detected could seem less important. Nonetheless, late decision-making has a low probability of success in controlling the outbreak, even at 20 cases. In this context, from a mathematical modeling perspective, a measure of mandatory social isolation such as quarantine was the only option for timely control of the epidemic 18, a measure that was finally adopted in Peru 19. Since this scenario is similar to several other countries with high social interaction and low case-resolving capacity 20, quarantine in countries like ours would be the only viable way to control the epidemic.
However, several questions remain. When is the right time to lift the quarantine or what conditions must be met to lift the quarantine? It is foreseeable that after quarantine ends many people will increase their social interaction disproportionately; if the control measures are decreased, it is possible that the post-quarantine R0 could be higher than pre-quarantine. In this case, the pandemic re-emergence would be uncontrollable, since it would no longer be based on one case, but on many more, as shown by some simulations in other contexts 21. What happened in China is a very instructive example, in this case the epidemic mitigation measures have not been lifted in a drastic, immediate manner, but rather gradually 22 23.
A very optimistic scenario is one where social interaction is reduced and accordingly the capacity of contagion decreases with R0 values of 1.5 or even less, this could be interpreted as a high probability of controlling of the epidemic post-quarantine. However, this optimistic scenario is not likely to take place, as it implies reducing social interaction and increasing case-resolving capacity in just a few weeks. In a more conservative scenario, where the R0 is 2, if we interrupt quarantine with 20 positive cases, we would need to track all contacts and early isolate people who test positive for COVID-19.
Therefore, it is understood that measures taken after quarantine will result in the control of the epidemic, or in the failure of the health system and the epidemic reemergence. Everything will depend on how much the value of the post-quarantine R0 decreases. In the conservative scenario, aggressive case and contact identification measures, border closure, home and hospital isolation, identification and quarantine of high-risk populations, and measures for mass events assessment may not increase the R0 after quarantine 24.
This analysis has several limitations, for example, it is based on a mathematical model that assumes that the disease spreads in a single closed society. On the contrary, Peru is divided into several regions that can be isolated from each other and thus, each one can have a different type of propagation dynamics. For each region, different problems arise when implementing and executing the control measures in a differentiated manner, which could generate confusion and inadequate preparation for the epidemic. Another limitation of this study is that it is based on assumptions that may not actually be verified, such as the number of cases. Without a mass screening test, the number of infected cases may not be accurate; however, such approximation can be determined by evaluating trends in epidemiological curves. This study recommends adequate logistics to guarantee effective contact tracing. This type of logistics varies in the case of a symptomatic or a non-symptomatic contact. Due to the lack of resources to guarantee such a measure, this is considered a limitation. Finally, the spread dynamics of COVID-19 in Peru is unknown, although the necessary calculations could be made. However, given the high level of under-report of COVID-19 cases, we would obtain an underestimated result. This is why we need to refer to values described in other studies.
The results are intended to be applicable to Peru, but are relevant for any region or country with similar case-resolving capacity, because the starting point is considering the maximum number of cases that can be supported and not the amount of affected population. Therefore, a region or country with less than 150 ICU beds will have to take more restrictive measures if it estimates to have over 3,000 cases. Likewise, the post-quarantine scenario we modeled could be equivalent to a pre-quarantine scenario in places with a late response.
In conclusion, social isolation of positive cases and contact tracing required many assumptions that were quickly exceeded, and if appropriate measures had not been taken, the probability of failing to control the epidemic would have been high. Our results justify the decision of implementing quarantine. The concern lies in the scenarios for the end of the quarantine. It is imperative that low social interaction is promoted in a sustained manner to avoid a new post-quarantine outbreak, as well as to continue with social isolation and the tracing of contacts of patients with COVID-19. Only then could there be a high probability of controlling the pandemic. In scenarios where mitigation measures are loosened and the spread of the disease returns to “normal” the probability of failure to control the pandemic is very high.
REFERENCES
1. Lazzerini M, Putoto G. COVID-19 in Italy: momentous decisions and many uncertainties. Lancet Glob Health. 2020. pii: S2214-109X(20)30110-8. doi: 10.1016/S2214-109X(20)30110-8. [ Links ]
2. Fong MW, Gao H, Wong JY, Xiao J, Shiu EYC, Ryu S, et al. Nonpharmaceutical Measures for Pandemic Influenza in Nonhealthcare Settings-Social Distancing Measures. Emerg Infect Dis. 2020;26(5):976-984. doi: 10.3201/eid2605.190995. [ Links ]
3. Walker P, Whittaker C, Watson O. Baguelin M, Ainslie K, Bhatia S, et al. Report 12:The Global Impact of COVID-19 and Strategies for Mitigation and Suppression [Internet]. London: WHO Collaborating Centre for Infectious Disease Modelling. Imperial College London; 2020. doi: 10.25561/77735. [ Links ]
4. Hellewell J, Abbott S, Gimma A, Bosse NI, Jarvis CI, Russell TW, et al. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob Health 2020;8(4):e488-e96. doi: 10.1016/S2214-109X(20)30074-7. [ Links ]
5. McBryde E. The value of early transmission dynamic studies in emerging infectious diseases. Lancet Infect Dis. 2020. pii: S1473-3099(20)30161-4. doi: 10.1016/S1473-3099(20)30161-4. [ Links ]
6. Chen TM, Rui J, Wang QP, Zhao ZY, Cui JA, Yin L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect Dis Poverty 2020;9(1):24. doi: 10.1186/s40249-020-00640-3. [ Links ]
7. Liu Y, Gayle AA, Wilder-Smith A, Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J Travel Med. 2020;27(2). pii: taaa021. doi: 10.1093/jtm/taaa021. [ Links ]
8. Park M, Cook AR, Lim JT, Sun Y, Dickens BL. A Systematic Review of COVID-19 Epidemiology Based on Current Evidence. J Clin Med. 2020;9(4). pii: E967. doi: 10.3390/jcm9040967. [ Links ]
9. Mizumoto K, Kagaya K, Zarebski A, Chowell G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Euro Surveill. 2020;25(10). doi: 10.2807/1560-7917.ES.2020.25.10.2000180. [ Links ]
10. Nishiura H, Kobayashi T, Miyama T, Suzuki A, Jung S, Hayashi K, et al. Estimation of the asymptomatic ratio of novel coronavirus infections (COVID-19). Int J Infect Dis. 2020. pii: S1201-9712(20)30139-9. doi: 10.1016/j.ijid.2020.03.020. [ Links ]
11. Li Q, Guan X, Wu P, Wang X, Zhou L, Tong Y, et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N Engl J Med. 2020;382(13):1199-1207. doi: 10.1056/NEJMoa2001316 [ Links ]
12. Donnelly CA, Ghani AC, Leung GM, Hedley AJ, Fraser C, Riley S, et al. Epidemiological determinants of spread of causal agent of severe acute respiratory syndrome in Hong Kong. Lancet 2003;361(9371):1761-6. doi: 10.1016/S0140-6736(03)13410-1. [ Links ]
13. Dong E, Du H, Gardner L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect Dis. 2020. pii: S1473-3099(20)30120-1. doi: 10.1016/S1473-3099(20)30120-1. [ Links ]
14. Xu B, Kraemer MUG, Xu B, Gutierrez B, Mekaru S, Sewalk K, et al. Open access epidemiological data from the COVID-19 outbreak. Lancet Infect Dis. 2020. pii: S1473-3099(20)30119-5. doi: 10.1016/S1473-3099(20)30119-5. [ Links ]
15. Fisher D, Wilder-Smith A. The global community needs to swiftly ramp up the response to contain COVID-19. Lancet. 2020;395(10230):1109-1110. doi: 10.1016/S0140-6736(20)30679-6. [ Links ]
16. COVID-19 National Emergency Response Center, Epidemiology & Case Management Team, Korea Centers for Disease Control & Prevention. Contact Transmission of COVID-19 in South Korea: Novel Investigation Techniques for Tracing Contacts. Osong Public Health Res Perspect. 2020;11(1):60-63. doi: 10.24171/j.phrp.2020.11.1.09. [ Links ]
17. Legido-Quigley H, Asgari N, Teo YY, Leung GM, Oshitani H, Fukuda K, et al. Are high-performing health systems resilient against the COVID-19 epidemic?. Lancet. 2020;395(10227):848-850. doi: 10.1016/S0140-6736(20)30551-1. [ Links ]
18. Wilder-Smith A, Freedman DO. Isolation, quarantine, social distancing and community containment: pivotal role for old-style public health measures in the novel coronavirus (2019-nCoV) outbreak. J Travel Med. 2020;27(2). pii: taaa020. doi: 10.1093/jtm/taaa020. [ Links ]
19. Decreto Supremo que declara Estado de Emergencia Nacional por las graves circunstancias que afectan la vida de la Nación a consecuencia del brote del COVID-19. Decreto supremo Nº 044-2020-PCM de 15 de marzo de 2020. El Peruano (15-03-2020). Disponible en: https://busquedas.elperuano.pe/normaslegales/decreto-supremo-que-declara-estado-de-emergencia-nacional-po-decreto-supremo-n-044-2020-pcm-1864948-2/. [ Links ]
20. Kandel N, Chungong S, Omaar A, Xing J. Health security capacities in the context of COVID-19 outbreak: an analysis of International Health Regulations annual report data from 182 countries. Lancet. 2020;395(10229):1047-1053. doi: 10.1016/S0140-6736(20)30553-5. [ Links ]
21. Ferguson NM, Laydon D, Nedjati-Gilani G, Imai N, Ainslie K, Baguelin M, et al. Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand [Internet]. London: Imperial College; 2020. doi: 10.25561/77482. [ Links ]
22. World Health Organization. Report of the who-china joint mission on coronavirus disease 2019 (covid-19) [Internet]. Geveva: OMS; 2020. Disponible en: https://www.who.int/docs/default-source/coronaviruse/who-china-joint-mission-on-covid-19-final-report.pdf. [ Links ]
23. Chen S, Yang J, Yang W, Wang C, Bärnighausen T. COVID-19 control in China during mass population movements at New Year. Lancet. 2020;395(10226):764-766. doi: 10.1016/S0140-6736(20)30421-9. [ Links ]
24. McCloskey B, Zumla A, Ippolito G, Blumberg L, Arbon P, Cicero A, et al. Mass gathering events and reducing further global spread of COVID-19: a political and public health dilemma. Lancet. 2020;395(10230):1096-1099. doi: 10.1016/S0140-6736(20)30681-4. [ Links ]
Received: March 24, 2020; Accepted: April 22, 2020










 texto en
texto en