Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Liberabit
versión impresa ISSN 1729-4827
liber. vol.22 no.1 Lima ene./jun. 2016
ARTÍCULOS
Discriminación de cantidad: efecto de la razón numérica sobre velocidad y precisión
Quantity discrimination: effect of number ratio over speed and accuracy
Jesica Formoso*, Juan Pablo Barreyro**, Silvia Jacubovich***, Marina Leiman**** e Irene Injoque-Ricle*****
*, **, ***, ***** Universidad de Buenos Aires (UBA), Argentina
**, ***, ****, ***** Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina
* jformoso@psi.uba.ar ** jbarreyro@psi.uba.ar *** sjacubov@psi.uba.ar **** marinaleiman@gmail.com
***** iinjoque@psi.uba.ar
RESUMEN
La habilidad de estimar y discriminar cantidades es de aparición temprana en el desarrollo y previa a la adquisición de un sistema numérico simbólico. El rendimiento en tareas de discriminación está modulado por la razón numérica que diferencia los conjuntos, de forma tal que razones más pequeñas resultan en comparaciones más lentas y menos efectivas. El objetivo del presente trabajo es analizar la precisión y velocidad con que niños de 4 y 6 años discriminan entre dos cantidades en función de la razón numérica que las diferencia. Método: se administró una tarea de discriminación no simbólica de cantidades (ad hoc) a 60 niños de 4 y 6 años de edad de la Ciudad Autónoma de Buenos Aires, Argentina. Se realizó un ANOVA de diseño mixto para analizar la cantidad de aciertos y los tiempos de reacción (TR) en función de la edad y la razón numérica que diferencia los conjuntos. Se utilizó la prueba de contraste de Bonferroni para detectar las diferencias en aciertos y TR entre cada razón. Resultados: (a) Los niños de 6 años mostraron TR más pequeños y mayor cantidad de aciertos que los niños de 4 años. Esto sugiere que la discriminación de cantidades atraviesa un proceso de desarrollo evolutivo. (b) Cuanto mayor fue la razón numérica en la diferenciación de los conjuntos, más efectiva fue la discriminación. Esto sugiere que la razón modula el rendimiento, independientemente de la edad del sujeto.
Palabras clave: Discriminación de cantidades, estimación, niños, razón numérica.
ABSTRACT
The ability to estimate and discriminate quantities is of early onset in the development and prior to the acquisition of a symbolic numerical system. The performance on tasks of discrimination is modulated by the number ratio that differentiates the sets, so that smaller reasons result in slower and less effective comparisons. The objective of the present study is to analyze the precision and speed by which 4 and 6 year old children discriminate between two quantities based on the number ratio that distinguishes them. Method: a discrimination task of non-symbolic quantities (ad hoc) was given to 60 children from 4 and 6 years old in the city of Buenos Aires, Argentina. A mixed ANOVA design was carried out to analyze the amount of hits and reaction times (RT) according to age, and the number ratio that differentiates the groups. The Bonferroni contrast test was used to detect the differences in hits and RT between each reasoning. Results: (a) children age 6 showed smaller RT and more hits than children age 4. This suggests that discrimination on the basis of quantities is undergoing a process of evolutionary development. (b) The greater the number ratio in the differentiation of the sets, the more effective the discrimination. This suggests that reason modulates performance regardless of the age of the subject.
Keywords: Quantity discrimination, estimate, children, number ratio
Introducción
La competencia matemática se define como la capacidad de entender, juzgar y hacer uso de habilidades matemáticas específicas en una variedad de situaciones de la vida cotidiana (Niss, 2003) y, en el ámbito escolar, es esperable que se vea reflejada en el desempeño del niño, no solo en el área de matemáticas, sino en su rendimiento general (Duncan et al., 2007). Es por ello que el conocimiento de las habilidades implicadas en esta competencia, así como su adquisición y desarrollo durante la infancia, permitirían ajustar la enseñanza de los conceptos matemáticos en el aula y, a su vez, la detección de posibles alteraciones.
Previamente a la adquisición de habilidades matemáticas complejas, como cálculo, la resolución de problemas aritméticos y la utilización de fracciones, los niños deben incorporar nociones acerca de lo que un número representa. En este sentido, se han identificado aspectos básicos de la cognición numérica que son de aparición temprana en la infancia, entre ellos, la habilidad de los niños de realizar una estimación aproximada de cuántos objetos conforman un conjunto finito que se les presenta sin necesidad de realizar un conteo verbal de los elementos (Dehaene, 2001; Feigenson, Dehaene y Spelke, 2004; Halberda, Ly, Wilmer, Naiman y Germine, 2012; Odic, Libertus, Feigenson y Halberda, 2013; Odic, Pietroski, Hunter, Lidz y Halberda, 2013; Xu, 2003; Xu, Spelke y Goddard, 2005). La habilidad de estimar cantidades, a diferencia de las habilidades matemáticas enseñadas en la escuela, es independiente de representaciones numéricas simbólicas, tales como los numerales arábigos (v. g., 4 u 8) o las palabras-número (v. g., cuatro u ocho), y la comprobación de la presencia de esta habilidad en niños preverbales y en algunos animales permite sostener esta hipótesis (Lipton y Spelke, 2004; McCrink y Wynn, 2004; Miletto Petrazzini, Agrillo, Izard y Bisazza, 2015; Miletto
Petrazzini, Agrillo, Piffer y Bisazza, 2014; Odic, Pietroski et al., 2013; Piffer, Agrillo y Hyde, 2012; Vallentin, Bongard y Nieder, 2012; Xu y Arriaga, 2007; Xu y Spelke, 2000). Este conocimiento intuitivo de magnitud se sustenta en un sistema cognitivo de representación de cantidades, denominado sistema numérico aproximado (ANS, del inglés aproximate number system), que permite al sujeto realizar una estimación rápida de cuántos elementos observa, así como discriminar entre conjuntos de objetos en base a su cantidad aun cuando no se trate de una apreciación exacta (Lindskog, Winman, Juslin y Poom, 2013; Mazzocco, Feigenson y Halberda, 2011a; Mazzocco, Feigenson y Halberda, 2011b). De hecho, el sistema posee una variabilidad que le es inherente y que genera determinados efectos: en primer lugar, la discriminación de magnitudes mediante el ANS tiende a ser más exacta y rápida cuanto más distantes son las cantidades a comparar (efecto de distancia) (Moyer y Bayer, 1976; Moyer y Landauer, 1967; Piazza, Izard, Pinel, Le Bihan y Dehaene, 2004). Asimismo, el grado de error y el tiempo de resolución del ANS aumenta cuanto mayor es el tamaño de las cantidades a evaluar (efecto de magnitud) (Cantlon y Brannon, 2006; Holloway y Ansari, 2009; Laski y Siegler, 2007; Nieder y Miller, 2003).
La conjunción de ambos efectos implica que la discriminación de cantidades se rige por la ley de Weber-Fechner, según la cual la mínima diferencia perceptible entre dos magnitudes resulta de una proporción constante entre las magnitudes a comparar (Dehaene, 2003; Starr, Libertus y Brannon, 2013). Se utiliza como constante la razón numérica que se obtiene de la división de la cantidad mayor sobre la menor. El rendimiento en tareas de comparación de cantidades se encuentra modulado por dicho valor. Es así que un sujeto discriminará más rápidamente y con mayor precisión entre dos cantidades diferenciadas por una razón de 2 (v. g., 4 y 8 elementos) que otras diferenciadas por una razón de 1.5 (v. g., 4 y 6 elementos) (Dehaene, 2003; Jordan y Brannon, 2006; Lindskog et al., 2013; Piazza et al., 2010).
Se ha observado también que la habilidad para estimar se desarrolla desde la infancia hasta la adultez. A medida que el niño crece puede comparar con efectividad cantidades diferenciadas por razones progresivamente más pequeñas (Cañizares y Reigosa-Crespo, 2011; Halberda y Feigenson, 2008; Halberda et al., 2012; Odic et al., 2013). Un adulto, por ejemplo, puede diferenciar un grupo de 7 elementos de uno de 8 elementos (razón 1.11) en más del 80 % de los casos (Halberda y Feigenson, 2008; Libertus, Odic y Halberda, 2012; Piazza et al., 2010). En cambio, para lograr el mismo nivel de efectividad, un bebé de 6 meses requiere que la diferencia entre los grupos se corresponda con una razón mínima de 2 (4 contra 8 elementos) (Xu y Spelke, 2000; Xu et al., 2005), mientras que un bebé de 10 meses ya es capaz de discriminar cantidades que se diferencian por una razón de 1.5 (8 contra 12 elementos) (Halberda y Feigenson, 2008; Lipton y Spelke, 2004; McCrink y Wynn, 2004; Xu y Arriaga, 2007).
A su vez, la precisión en la discriminación puede variar de un sujeto a otro. Incluso, ciertos estudios sugieren que estas diferencias individuales pueden predecir el rendimiento en tareas matemáticas simbólicas, tanto en niños como en adultos (Geary et al., 2009; Guillaume, Nys, Mussolin y Content, 2013; Halberda, Mazzocco y Feigenson, 2008; Inglis, Attridge, Batchelor y Gilmore, 2011; Libertus et al., 2013; Libertus et al., 2012; Mazzocco et al., 2011a; Sasanguie, Göbel, Moll, Smets y Reynvoet, 2013). Se ha observado, además, que si bien sería esperable que luego de la adquisición de un sistema simbólico de procesamiento numérico los sujetos adultos realizasen juicios exactos de cantidad y abandonasen el uso del ANS para la comparación de cantidades, este no parece ser el caso en tanto los sujetos continúan utilizando la estimación aproximada para la realización de todo tipo de tareas numéricas, incluyendo la discriminación (Lyons y Beilock, 2011; Park y Brannon, 2013). Estas apreciaciones permiten suponer que el ANS constituye la base semántica sobre la que posteriormente se asienta el sistema numérico simbólico que permite luego acceder al cálculo exacto (Barth, Beckmann y Spelke, 2008; Mundy y Gilmore, 2009).
Conocer en profundidad el desarrollo de la habilidad para estimar y discriminar cantidades desde la infancia hasta la adultez, así como los factores que inciden sobre esta, permitiría eventualmente precisar el abordaje de los conceptos matemáticos a nivel escolar y, al mismo tiempo, detectar posibles alteraciones previas al ingreso del niño en el sistema de educación formal.
El objetivo general del presente trabajo consiste en analizar la precisión y velocidad con que niños de 4 y 6 años discriminan entre dos conjuntos con distinta cantidad de elementos en función de la razón numérica que los diferencia. Para ello, se analizará la cantidad de respuestas correctas para los diferentes estímulos según la edad como medida de precisión. Está previsto observar diferencias significativas entre los grupos etarios a favor de los niños mayores. Se analizarán, además, los tiempos de respuesta de cada edad ante los diferentes estímulos como medida de velocidad. Se espera encontrar que los niños de 6 años tengan tiempos de reacción significativamente menores que los de 4 años. Asimismo, se prevé que la discriminación de cantidades se encuentre modulada por la razón numérica que diferencia los conjuntos a comparar.
Método
Participantes
La muestra estuvo conformada por 60 niños de ambos sexos divididos en dos grupos en función de la edad: 30 sujetos de 4 años [media de edad en meses = 51.70; DE = 2.54; 16 mujeres (53.30 %) y 14 varones] y 30 sujetos de 6 años [media de edad en meses = 77,53; DE = 3.80; 15 mujeres (50.00 %) y 15 varones], alumnos de dos escuelas de gestión privada de la Ciudad Autónoma de Buenos Aires, Argentina. Los niños participaron con el consentimiento escrito de los padres y la información recabada fue tratada de manera anónima y confidencial. Fueron excluidos del estudio niños con trastornos auditivos o del lenguaje, alteraciones neurológicas, psiquiátricas o con un CI inferior a 80.
Materiales
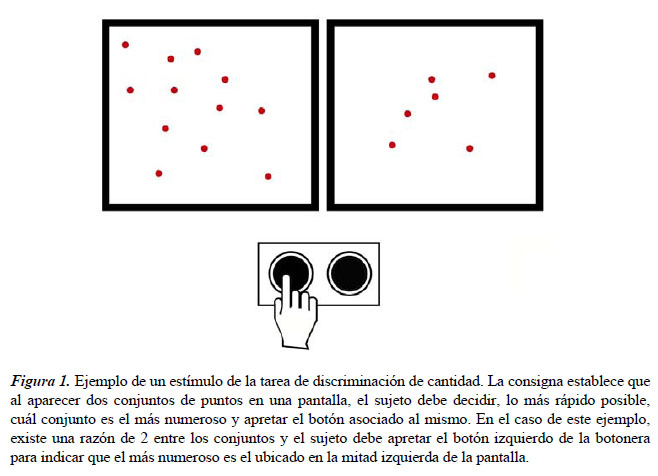
Tarea de discriminación de cantidades. Esta tarea forma parte de la Batería de Habilidades Matemáticas Básicas (ad hoc) y consiste en la presentación simultánea de dos conjuntos de puntos en la pantalla de una computadora, uno a cada lado de la misma (ver Figura 1). En cada ensayo, el niño debe decidir lo más rápido posible cuál de los conjuntos observados simultáneamente es el más numeroso e indicarlo presionando el botón izquierdo o derecho de una botonera, según corresponda a su ubicación espacial en la pantalla. Cada estímulo se presenta durante 3 segundos para evitar que los sujetos recurran al conteo verbal. Los conjuntos a comparar en cada presentación se diferencian por una de 4 razones numéricas: 3, 2, 1.50 y 1,15. Por ejemplo, para la razón numérica, 3 los sujetos deben comparar 4 vs. 12 puntos, 8 vs. 24 puntos y 16 vs. 48 puntos.
Se registra el tiempo de reacción (TR) como medida de velocidad de procesamiento (tiempo transcurrido entre la presentación de los estímulos en la pantalla y la presión la tarea se controla a través del paquete de software de del botón correspondiente por parte del niño) y la cantidad experimentación OpenSesame (Mathôt, Schreij y de respuestas correctas como medida de precisión. Toda Theeuwes, 2012).
Procedimiento
Se les administró a los participantes la tarea de discriminación de cantidades en una única sesión individual, en un ambiente libre de ruidos y distracciones dentro de la institución escolar. Los niños participaron con el consentimiento de los padres, quienes asistieron a una reunión informativa previa en la que se explicaron los objetivos de la investigación y el tipo de tareas a realizar y se les aseguró la confidencialidad de la información y el anonimato de la participación.
Análisis de datos
Para analizar los datos, se promediaron las respuestas a los estímulos con igual razón numérica entre la cantidad de puntos de los conjuntos. Con el fin de estudiar la presencia o ausencia de diferencias significativas en la cantidad de respuestas correctas en función de la edad y la razón numérica, se realizó un análisis de varianza de diseño mixto 4 x 2, tomando como variable independiente intersujeto la edad (4 vs. 6 años), y como variable independiente intrasujeto las diferentes razones numéricas (3, 2, 1.50 y 1.15). Para el análisis post hoc se empleó la prueba de contraste de Bonferroni. El mismo análisis se realizó sobre los TR.
Resultados
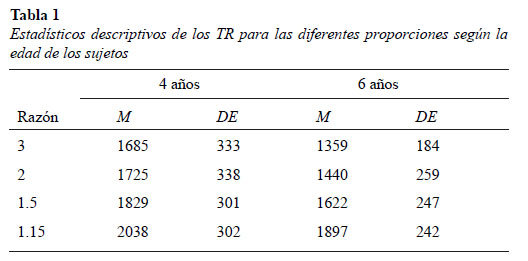
En primer lugar, se analizaron las distribuciones de los TR medidos en milisegundos para las diferentes razones (3, 2, 1.50 y 1.15), agrupando a los sujetos según su edad (ver Tabla 1).
Con el objetivo de estudiar el efecto de la razón sobre los TR en ambas edades, se realizó un análisis mixto de varianza que mostró un efecto principal significativo del factor edad sobre los TR (F(1, 58)= 30.14, MSE = 114 425, p < .001, η2 = .34), así como un efecto principal significativo del factor razón sobre los TR (F(3, 174) = 35.33, MSE = 66 471, p < .001, η2 = .38). Por otra parte, no se observó una interacción entre los factores razón*edad (F(3, 174)= 1.53, MSE = 66 471, p = .21, η2 = .03).
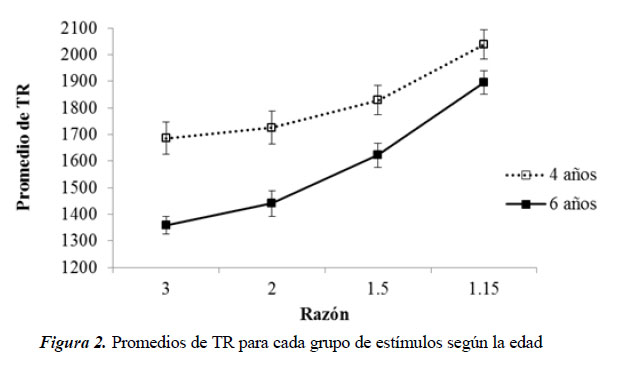
Se realizaron comparaciones por pares entre los diferentes niveles del factor razón. Para el control de la tasa de error, los niveles críticos y los intervalos de confianza fueron ajustados mediante la corrección de Bonferroni. El resultado de dichas comparaciones arrojó que no existen diferencias significativas en los TR entre las razones 3 y 2, pero sí entre estas y las razones 1.5 y 1.15, siendo los TR de estas últimas significativamente mayores (p < .01). A su vez, se observó que la discriminación de los conjuntos es significativamente más rápida para la razón 1.5 que para la razón 1.15 (p < .001). Estas diferencias se replican en ambas edades. En la Figura 2 se muestra el TR promedio para cada razón numérica por cada grupo de edad.
Al comparar el rendimiento por edades, se verificó que los niños de 6 años responden significativamente más rápido que los niños de 4 años en todas las razones.
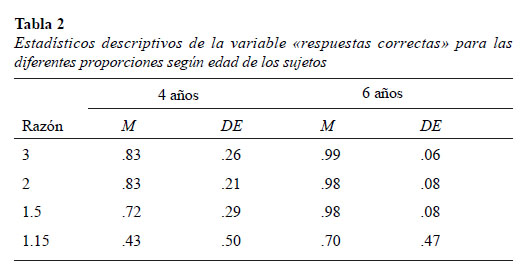
Posteriormente, se analizaron las distribuciones de las respuestas correctas para las diferentes razones agrupando a los sujetos según su edad (ver Tabla 2).
En el análisis mixto de varianza se encontró un efecto principal significativo del factor edad sobre la variable respuestas correctas (F(1, 58) = 20.39, MSE = .12, p < .001, η2 = .26), así como un efecto principal significativo del factor razón sobre la variable respuestas correctas (F(3, 174)= 22.04, MSE = 0.07, p < .001, η2 = .28). Por otra parte, no se observó una interacción significativa de los factores razón*edad en la variable respuestas correctas (F(3, 174)=.86, MSE = .05, p = .46, η2 = .02).
Para ambos grupos de edad se realizaron, además, comparaciones por pares de los diferentes niveles del factor razón. Para el control de la tasa de error, los niveles críticos y los intervalos de confianza fueron ajustados mediante la corrección de Bonferroni.
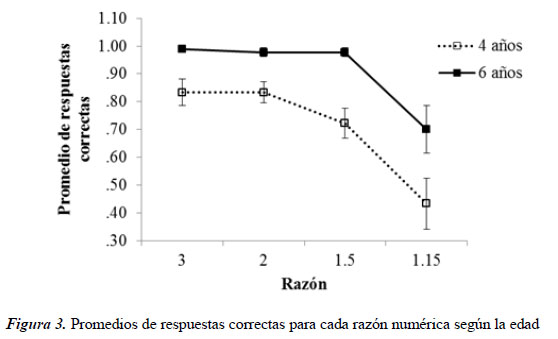
En las comparaciones por pares no se observaron diferencias significativas en las respuestas correctas entre las razones 3, 2 y 1.5, pero sí entre estas y la razón 1.15, para la cual la cantidad de respuestas correctas es significativamente menor (p < .001). Este comportamiento se reproduce en ambas edades. En la Figura 3 se muestran los promedios de respuestas correctas para cada razón numérica agrupados por edad.
Al comparar el rendimiento por edades en cada nivel del factor razón, se verificó que los niños de 6 años responden con mayor precisión, es decir, presentan mayor número de respuestas correctas que los niños de 4 años en todas las razones.
Discusión
La habilidad para estimar y discriminar cantidades de forma aproximada es un aspecto básico de la cognición numérica. Diferentes autores sostienen que esta habilidad de aparición temprana refleja el funcionamiento de un sistema cognitivo preverbal para el procesamiento de cantidades de forma aproximada (ANS), el cual se rige por la ley de Weber-Fechner (Dehaene, 2003; Jordan y Brannon, 2006; Lindskog et al., 2013; Piazza et al., 2010). Según esta, el rendimiento en una tarea de comparación de cantidades depende de la razón numérica que diferencia ambos conjuntos, lográndose estimaciones más precisas y rápidas cuanto mayor es la razón que los distingue (se discriminan más rápidamente conjuntos con una razón de 3 (v.g., 3 y 9 elementos) que aquellos con una razón de 2 (v.g., 3 y 6 elementos).
A su vez, se sostiene que esta habilidad atraviesa un proceso de desarrollo de la infancia a la adultez, y se observa que la velocidad y precisión en la comparación aumenta con la edad, por lo que el sujeto podrá discriminar efectivamente cantidades diferenciadas por razones progresivamente más pequeñas (Cañizares y Reigosa-Crespo, 2011; Halberda y Feigenson, 2008; Halberda et al., 2012; Odic, Libertus et al., 2013).
El objetivo del presente trabajo consistió en analizar la precisión y la velocidad con que los niños de 4 y 6 años discriminan conjuntos con diferente cantidad de elementos, en función de la razón numérica que los distingue.
Resultaba esperable que se observen diferencias significativas en la precisión y la velocidad entre los grupos etarios a favor de los niños mayores. A su vez, se esperaba que la discriminación de cantidades se encuentre modulada por la razón numérica entre los conjuntos a comparar. Para ello, se administró a los sujetos una tarea de discriminación de cantidades. Se registró la cantidad de respuestas correctas y los tiempos de reacción para cada edad, agrupados según la razón numérica de los estímulos.
Los datos arrojados por el análisis de varianza permitieron observar que la edad de los sujetos incidió tanto sobre la velocidad como sobre la precisión para discriminar cantidades. Los niños de 6 años mostraron TR significativamente menores y mayor proporción de aciertos que los niños de 4 años en todos los niveles del factor razón numérica. En ese sentido, el efecto de la edad sobre el rendimiento en esta tarea resultó ser independiente de la razón.
Estos resultados son congruentes con los obtenidos en estudios previos (Cañizares y Reigosa-Crespo, 2011; Halberda y Feigenson, 2008; Odic, Libertus et al., 2013). En tanto, la reducción en el tiempo de resolución y el aumento en la precisión en la tarea de discriminación de los 4 a los 6 años permiten inferir que la habilidad para estimar y discriminar cantidades evoluciona entre estas edades y que esta manifestación puede corresponderse con un desarrollo del ANS.
En relación al factor razón numérica, este mostró tener efecto tanto sobre la velocidad como sobre la precisión en la discriminación de cantidades. La distribución de los TR no mostró diferencias significativas entre las razones 3 y 2 (por ejemplo, 8 vs. 24 puntos y 8 vs. 16 puntos), pero sí entre estas y las razones 1.5 y 1.15 (8 vs. 12 y 7 vs. 8, respectivamente) y, simultáneamente, entre la razón 1.5 y la razón 1.15. Además, de acuerdo con la distribución de las respuestas, para la razón 1.15, la cantidad de aciertos fue significativamente menor que para las restantes en ambos grupos de edad. El efecto de la razón numérica sobre el rendimiento de los sujetos resultó ser independiente de la edad de estos; en tanto, no se observó una interacción entre ambos factores.
En este sentido, la evidencia obtenida es coherente con los estudios antes mencionados, mientras parece modular el rendimiento de los niños independientemente de la edad (Dehaene, 2003; Lindskog et al., 2013; Starr et al., 2013).
Si bien excede a los límites del presente estudio, sería de gran interés el análisis de la precisión y velocidad de estimación y discriminación de cantidades en otros grupos etarios para obtener mayor evidencia acerca de la noción de desarrollo de esta habilidad y poder establecer en qué momento los niños alcanzan el rendimiento observado en adultos. Además, considerando que esta habilidad, así como el sistema que le subyace, se encuentra en la base del conocimiento matemático que se adquiere posteriormente, resulta de central importancia entender el efecto de su desarrollo sobre el aprendizaje de las matemáticas formales. De igual manera, conocer el efecto del entrenamiento en tareas de estimación y discriminación numérica sobre el desarrollo del ANS podría, eventualmente, traducirse en estrategias concretas para la enseñanza de habilidades matemáticas básicas en la educación de nivel inicial y posibles técnicas para el tratamiento de alteraciones en esta área.
Referencias
Barth, H., Beckmann, L., & Spelke, E. S. (2008). Nonsymbolic, approximate arithmetic in children: abstract addition prior to instruction. Developmental Psychology, 44(5), 1466-1477. doi: 10.1037/a0013046
Cañizares, D. C. & Reigosa-Crespo, V. (2011). Calibrando la línea numérica mental: evidencias desde el desarrollo típico y atípico. Revista Neuropsicología, Neuropsiquiatría y Neurociencias, 11(1), 17-31.
Cantlon, J. F. & Brannon, E. M. (2006). Shared system for ordering small and large numbers in monkeys and humans. Psychological Science, 17(5), 401-406. doi: 10.1111/ j.1467-9280.2006.01719.x
Dehaene, S. (2001). Precis of the number sense. Mind & Language, 16, 16-36. doi: 10.1111/1468-0017.00154
Dehaene, S. (2003). The neural basis for the Weber-Fechner law: a logarithmic mental number line. Trends in Cognitive Sciences, 7(4), 145-147. doi: 10.1016/s1364-6613(03)00055-x
Duncan, G., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., … Japel, C. (2007). School readiness and later achievement. Developmental Psychology, 43(6), 1428-1446. doi: 10.1037/0012-1649.44.1.217
Feigenson, L., Dehaene, S., & Spelke, E. (2004). Core systems of number. Trends in Cognitive Sciences, 8(7), 307-314. doi: 10.1016/j.tics.2004.05.002
Geary, D. C., Bailey, D. H., Littlefield, A., Wood, P., Hoard, M. K., & Nugent, L. (2009). First-grade predictors of mathematical learning disability: A latent class trajectory analysis. Cognitive Development, 24(4), 411-429. doi: 10.1016/j.cogdev.2009.10.001
Guillaume, M., Nys, J., Mussolin, C., & Content, A. (2013). Differences in the acuity of the approximal number system in adults: the effect of mathematical ability. Acta Psychologica, 144(3), 506-512. doi: 10.1016/j.actpsy.2013.09.001
Halberda, J. & Feigenson, L. (2008). Developmental change in the acuity of the «Number Sense»: The approximate number system in 3-, 4- 5- and 6-year-olds and adults. Developmental Psychology, 44(5), 1457-1465. doi: 10.1037/ a0012682
Halberda, J., Ly, R., Wilmer, J. B., Naiman, D. Q., & Germine, L. (2012). Number sense across the lifespan as revealed by a massive Internet-based sample. Proceedings of the National Academy of Sciences, 109(28), 11116-11120. doi: 10.1073/ pnas.1200196109
Halberda, J., Mazzoco, M. M., & Feigenson, L. (2008). Individual differences in non-verbal number acuity correlates with maths achievement. Nature, 455, 665-668 doi: 10.1038/ nature07246
Holloway, I. D. & Ansari, D. (2009). Mapping numerical magnitudes onto symbols: the numerical distance effect and individual differences in children’s mathematics achievement. Journal of Experimental Child Psychology, 103(1), 17-29. doi: 10.1016/j.jecp.2008.04.001
Inglis, M., Attridge, N., Batchelor, S., & Gilmore, C. (2011). Non-Verbal number acuity correlates with symbolic mathematics achievemente: But only children. Pshyconomic Bulletin & Review, 18(6), 1222-1229. doi: 10.3758/s13423011-0154-1
Jordan, K. E. & Brannon, E. M. (2006). Weber’s Law influences numerical representations in rhesus macaques (Macaca mulatta). Animal Cognition, 9(3), 159-172. doi: 10.1007/ s10071-006-0017-8
Laski, E. V. & Siegler, R. S. (2007). Is 27 a big number? Correlational and causal connections among numerical categorization, number line estimation, and numerical magnitude comparison. Child Development, 78(6), 17231743. doi: 10.1111/j.1467-8624.2007.01087.x
Libertus, M. E., Feigenson, L., & Halberda, J. (2013). Is approximate number precision a stable predictor of math ability? Learning and Individual Differences, 1(25), 126-133. doi: 10.1016/j.lindif.2013.02.001
Libertus, M. E., Odic, D., & Halberda, J. (2012). Intuitive sense of number correlates with math scores on collage-entrance examination. Acta Psychologica, 141(3), 373-379. doi: 10.1016/j.actpsy.2012.09.009
Lindskog, M., Winman, A., Juslin, P., & Poom, L. (2013). Measuring acuity of the approximate number system reliably and validly: the evaluation of an adaptive test procedure. Frontiers in Psychology, 4, 510. doi: 10.3389/ fpsyg.2013.00510
Lipton, J. & Spelke, E. (2004). Discrimination of large and small numerosities by human infants. Infancy, 5(3), 271-290. doi: 10.1207/s15327078in0503_2
Lyons, I. M. & Beilock, S. L. (2011). Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition, 121(2), 256-261. doi: 10.1016/ j.cognition.2011.07.009
Mathôt, S., Schreij, D., & Theeuwes, J. (2012). OpenSesame: An open-source, graphical experiment builder for the social sciences. Behavior Research Methods, 44(2), 314-324. doi: 10.3758/s13428-011-0168-7
Mazzocco, M., Feigenson, L., & Halberda, J. (2011a). Preschoolers’ precision of the approximate number system predicts later school mathematics performance. PLoS One, 6(9), e23749. doi: 10.1371/journal.pone.0023749
Mazzocco, M., Feigenson, L., & Halberda, J. (2011b). Impaired Acuity of the Approximate Number System Underlies Mathematical Learning Disability (Dyscalculia). Child Development, 82(4), 1224-1237. doi: 10.1111/j.14678624.2011.01608.x
McCrink, K. & Wynn, K. (2004). Large-number addition & subtraction by 9-month-old infants. Psychological Science, 15(11), 776-781. doi: j.0956-7976.2004.00755.x
Miletto, M., Agrillo, C., Izard, V., & Bisazza, A. (2015). Relative versus absolute numerical representation in fish: Can guppies represent «fourness»? Animal Cognition. doi: 10.1007/ s10071-015-0868-y
Miletto, M., Agrillo, C., Piffer, L., & Bisazza, A. (2014). Ontogeny of the capacity to compare discrete quantities in fish. Dev Psychobiol, 56(3), 529-536. doi: 10.1002/dev.21122
Moyer, R. S. & Bayer, R. H. (1976). Mental comparison and the symbolic distance effect. Cognitive Psychology, 8(2), 228-246. doi: 10.1016/0010-0285(76)90025-6
Moyer, R. S. & Landauer, T. K. (1967). Time required for judgement of numerical inequality. Nature, 215(5109), 15191520. doi: 10.1038/2151519a0
Mundy, E. & Gilmore, C. K. (2009). Children’s mapping between symbolic and nonsymbolic representations of number. Journal of Experimental Child Psychology, 103(4), 490-502. doi: 10.1016/j.jecp.2009.02.003
Nieder, A. & Miller, E. K. (2003). Coding of cognitive magnitude: Compressed scaling of numerical information in the primate prefrontal cortex. Neuron, 37(1), 149-157. doi: 10.1016/ s0896-6273(02)01144-3
Niss, M. (2003). Mathematical competencies & the learning of mathematics: The Danish KOM project. Documento presentado en 3rd Mediterranean Conference on Mathematical Education, Atenas.
Odic, D., Libertus, M. E., Feigenson, L., & Halberda, J. (2013). Developmental change in the acuity of approximate number and area representations. Developmental Psychology, 49(6), 1103-1112. doi: 10.1037/a0029472
Odic, D., Pietroski, P., Hunter, T., Lidz, J., & Halberda, J. (2013). Young children’s understanding of «more» and discrimination of number and surface area. Journal of Experimental Psychology: Learning, Memory and Cognition, 39(2), 451-461. doi: 10.1037/a0028874
Park, J. & Brannon, E. M. (2013). Training the approximate number system improves math proficiency. Psychological Science, 24(10), 2013-2019. doi: 10.1177/ 0956797613482944
Piazza, M., Facoetti, A., Trussardi, A. N., Berteletti, I., Conte, S., Lucangeli, D., . . . Zorzi, M. (2010). Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition, 116(1), 33-41. doi: 10.1016/j.cognition.2010.03.012
Piazza, M., Izard, V., Pinel, P., Le Bihan, D., & Dehaene, S. (2004). Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron, 44(3), 547-555. doi: 10.1016/j.neuron.2004.10.014
Piffer, L., Agrillo, C., & Hyde, D. C. (2012). Small and large number discrimination in guppies. Anim Cogn, 15(2), 215-221. doi: 10.1007/s10071-011-0447-9
Sasanguie, D., Göbel, S., Moll, K., Smets, K., & Reynvoet, B. (2013). Approximate number sense, symbolic number processing, or number-space mappings: what underlies mathematics achievement? Journal of Experimental Child Psychology, 114(3), 418-431. doi: 10.1016/j.jecp.2012.10.012
Starr, A. B., Libertus, M. E., & Brannon, E. M. (2013). Infants Show Ratio-dependent Number Discrimination Regardless of Set Size. Infancy, 18(6). doi: 10.1111/infa.12008
Vallentin, D., Bongard, S., & Nieder, A. (2012). Numerical rule coding in the prefrontal, premotor, and posterior parietal cortices of macaques. The Journal of Neuroscience, 32(19), 6621-6630. doi: 10.1523/JNEUROSCI.5071-11.2012
Xu, F. (2003). Numerosity discrimination in infants: Evidence for two systems of representations. Cognition, 89(1), B15B25. doi: 10.1016/s0010-0277(03)00050-7
Xu, F. & Arriaga, R. L. (2007). Number discrimination in 10month-old infants. British Journal of Developmental Psychology, 25, 103-108. doi: 10.1348/026151005x90704
Xu, F. & Spelke, E. (2000). Large number discrimination in 6month-old infants. Cognition, 74(1), 1-11. doi: 10.1016/ s0010-0277(99)00066-9
Xu, F., Spelke, E., & Goddard, S. (2005). Number sense in human infants. Developmental Science, 8(1), 88-101. doi: 10.1111/ j.1467-7687.2005.00395.x
* Facultad de Psicología, Universidad de Buenos Aires (UBA), Argentina.
** Facultad de Psicología, Universidad de Buenos Aires (UBA), Argentina.
Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina.
*** Facultad de Psicología, Universidad de Buenos Aires (UBA), Argentina.
**** Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina.
***** Facultad de Psicología, Universidad de Buenos Aires (UBA), Argentina.
Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina.
La presente investigación fue financiada por la Secretaría de Ciencia y Técnica de la Universidad de Buenos Aires, Argentina.
Recibido: 19 de agosto de 2015
Aceptado: 02 de marzo de 2016