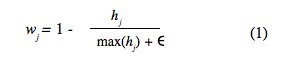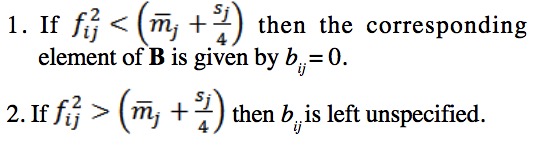Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Liberabit
versión impresa ISSN 1729-4827
liber. vol.25 no.1 Lima jun./dic. 2019
http://dx.doi.org/10.24265/liberabit.2019.v25n1.08
ARTÍCULOS DE INVESTIGACIÓN
Robust Promin: a method for diagonally weighted factor rotation
Robust Promin: un método para la rotación de factores de diagonal ponderada
Urbano Lorenzo-Seva a, *
http://orcid.org/0000-0001-5369-3099
Pere J. Ferrando a
http://orcid.org/0000-0002-3133-5466
a Department of Psychology, Universitat Rovira i Virgili, Spain
Autor corresponsal: *urbano.lorenzo@urv.cat
Abstract
Background: oblique rotation of factors is usually performed in exploratory factor analysis in order to achieve the best and simplest interpretation of the solution based on the prescribed number of factors. Currently available algorithms, however, do not take into account the fluctuation of the correlations on which the factor solution is based. If such correlations’ stability is low, the rotated solution obtained in a specific sample may substantially differ from the rotated solutions obtained in different samples from the same population. Objetive: the present paper proposes a modified version of the Promin rotation designed to achieve simple and stable rotated solutions through the samples. Conclusions: the usefulness of Robust Promin is illustrated by using an empirical example based on a real dataset. The procedure proposed in this paper has been implemented in the FACTOR factor analysis program version 10.9.
Keywords: oblique rotation, robust factor analysis, exploratory factor analysis, unrestricted factor analysis.
Resumen
Antecedentes: la rotación oblicua de los factores es una práctica habitual en el análisis factorial exploratorio. Habitualmente su finalidad es obtener la solución más interpretable y a la vez más simple con base en el número de factores prescrito. Los algoritmos actualmente disponibles, sin embargo, no tienen en cuenta la fluctuación de las correlaciones en las que se basa la solución factorial. Si la estabilidad de dichas correlaciones es baja, entonces la solución rotada obtenida en una muestra en particular puede diferir bastante de las que se obtendrían en diferentes muestras procedentes de la misma población. Objetivos: en este artículo se propone una versión modificada de la rotación Promin, cuyo objetivo es obtener soluciones que sean a la vez simples y estables a través de muestras. Conclusiones: el funcionamiento de Promin robusto se ilustra mediante un ejemplo empírico basado en datos reales. El procedimiento propuesto en el artículo ha sido implementado en la versión 10.9 del programa de análisis factorial FACTOR..
Palabras clave: rotación oblicua, análisis factorial robusto, análisis factorial exploratorio, análisis factorial no restricto
Introduction
Once a factorial solution with a specified number of factors has been obtained, it should be substantively interpreted. Unfortunately, the direct or canonical orthogonal loading matrix is obtained under convenience constraints aimed at achieving determinacy, and is in general substantively uninterpretable. In exploratory factor analysis, the factorial model in the population is unknown and any rotated solution can be considered to be interpreted (see, for example, Schönemann & Wang, 1972, or Browne, 2001). To arrive at a substantively interpretable solution, the orthogonal loading matrix is typically rotated to maximize the simple structure criterion (Thurstone, 1947). As Browne (2001) pointed out, the most advisable rotation approach is to allow factors to correlate (i.e., to rotate the factors by using oblique rotation methods).
Because all rotation approaches aim to maximize a loading simplicity index, the rotation procedure is expected to arrive at a simple and interpretable solution based on the data obtained in a specific sample. However, if the focus is only set on maximizing factor simplicity, the rotated solution can fit the sample data very well but misses the ‘true’ factor solution in the population. This is most likely when the correlations among variables are unstable and the sampling variability is larger. In turn, this basic instability is expected to lead to rotated solutions that are also unstable across samples.
Some direct factor procedures available at present take into account the differential stability of the inter- variable correlation matrix. These procedures are expected to be more robust than standard procedures to the problem of sampling variability, and are usually based on a minimization criterion in which the residual correlations are weighted by their estimated asymptotic variance. These procedures are expected to outperform standard procedures when (a) the sampling fluctuation (asymptotic variances) varies considerably among correlations, and (b) the asymptotic variances (i.e., the weights) can be estimated accurately. Condition (a) occurs in particular when the factor analysis is based on a tetrachoric/polychoric correlation matrix (see, e.g., Ferrando & Lorenzo- Seva, 2013).
In the present paper we extend the basic principle above to the rotation stage in order to obtain a rotated loading matrix that is more robust to (differential) sampling fluctuation. As we adapt our approach to the rotation method known as Promin (Lorenzo-Seva, 1999), we shall name the new rotation method Robust Promin.
Robust Promin rotation
One of the most popular oblique rotation hat first computes a perfectly simple matrix, and then uses this matrix as a target pattern in the rotation. Examples of this approach are Promax (Hendrickson & White, 1964), Simplimax (Kiers, 1994) and Promin (Lorenzo- Seva, 1999).
In order to build the target matrix, Promax first computes an orthogonal rotation (usually Varimax, Kaiser, 1958). Then each of the elements in the orthogonally-rotated loading matrix is manipulated so that they become either close to zero, or close to one. One of these manipulations increases each value to an arbitrary power (usually a power of four). Once the target is available, an oblique congruence rotation (Mosier, 1939) is computed. The major drawback of Promax is that the final position of the rotated factors depends on the power that is used when building the target matrix.
Simplimax shares some characteristics with Promax. For example, it is also a two-step rotation method, and it is recommended to carry out a previous Varimax rotation (clever start) in order to build a target matrix. In addition to the clever start, a large number of random orthogonal starts are computed. For each one of these previous rotations, a set of partially specified target matrices are computed: each target matrix is based on a different k number of specified values. For each target at hand, the k values that are closest to zero in the previously rotated loading matrix are set to zero in the target matrix. The other elements are set as non-specified values in the target. Each target matrix is used to compute a partially specified oblique Procrustes rotation (Browne, 1972) in which the specified elements are the ones set to zero in the target matrix. As a (large) number of targets are built, the rotation produces a (large) number of rotated solutions, and the optimal one has to be chosen. The major drawback of Simplimax is that it can sometimes be difficult to decide which solution has the optimal k number of zeros in the partially specified target, and non-expert researchers can find it complex to use. In addition to this problem of choice, it is also difficult to decide how many factors to retain when applying exploratory factor analysis. It must be noted that Simplimax can give good results even with complex solutions in which many of the variables have a complexity larger than one. The conclusion is that Simplimax is a powerful and efficient rotation method but not always easy to use.
Promin was proposed as an oblique rotation method that combines strategies already used in other rotation methods (like Promax and Simplimax) but adapted so that no decisions need to be taken. In this regard, Promin turns out to be a simple-to-use rotation method. Its usefulness in applied research has already been proved by the numerous researchers that use Promin in their daily analyses. In the original proposal, Promin focuses on maximizing the simplicity of the rotated solution, even when some of the variables are not simple but complex (i.e., some variables show a salient loading value on more than one factor; see Ferrando & Lorenzo-Seva, 2014). In our new proposal, we aim to propose a rotation method that focuses (1) on maximizing the simplicity of the rotated solution, and (2) on the loading values of the variables whose correlations with the remaining variables are the most stable. So, the rotated loading matrix obtained with Robust Promin is expected to be both simple and stable across samples.
Like Promin, Robust Promin is a two-step rotation method. The first step builds a partially specified target matrix; the second step rotates the loading matrix using the partially specified oblique Procrustes rotation.
First step: partially specified target matrix
Promin builds a partially specified target matrix using a previous Weighted Varimax rotation as a starting point (Cureton & Mulaik, 1975). In the context of Varimax rotation, Kaiser (1958) proposed to row-normalize the variables of the unrotated loading matrix so that all the variables have the same influence, and the final position of the rotated factors can be decided. In the context of Weighted Varimax rotation, Cureton and Mulaik proposed that the variables expected to be the simplest should be detected before the rotation is computed. On the basis of this previous information, the variables are weighted so that the simplest variables are precisely the ones that have the largest influence on the decision about the final position of the rotated factors.
In Robust Promin we propose using a weighted scheme, the aim of which is different from the one proposed by Cureton and Mulaik. Our aim is to give more influence to the variables that have the most stable set of correlations with the other variables. Given a particular variable vj in a set of m variables, this variable has m – 1 correlations with the other variables. The stability of the set of correlations related to vj can be quantified as the average of the m – 1 diagonal values in the asymptotic variance/covariance matrix in which the variable vj is involved. Let us refer to this average as hj . Then, the weight wj for variable vj is obtained as where E is a residual value (for example, E = .0001).
The variable with the largest average of asymptotic variances (i.e., the variable with the least stable set of correlations) will have a weight value (wj) close to zero. On the other hand, a variable with a mean asymptotic variance of zero (i.e., a variable with a set of perfectly stable correlations) will have a weight value (wj) of one.
In order to obtain the partially specified target B, an orthogonal loading matrix that maximizes factor simplicity must be computed. If W is a diagonal matrix which weights wj in the diagonal positions, A is the direct unrotated loading matrix, and S = varimax (WA), (2) then the product P = WAS is an orthogonal rotated loading matrix in which the simplicity is maximized for the variables that show the most stable set of correlations. Let V be a diagonal matrix that is computed as V = diag (PP ́) - ½ (3)
This means that the F matrix can be computed as the product F = VP (4) where F is now the corresponding row-normalized matrix of P. Finally, the mean and the standard deviation of the squared elements of each column in the F matrix is computed. Let m be the vector with these means, and s be the vector with these standard deviations. So the partially specified target matrix B is built as follows:
The target B has two kinds of values: zero and unspecified. The values equal to zero are the specified values, while the unspecified values are free values in the rotation. So, matrix B is a partially specified target matrix.
Second step: partially specified oblique Procrustes rotation
Once the simple partially specified target has been set, Promin minimizes the function g, g(T) = ||AT - B||2 (5) where T is constrained to diag ( T -1 T -1 ́ ) = I . Browne (1972) proposed the solution to this partially specified Procrustes rotation criterion. The final rotated loading matrix L is obtained as L = AT (6), and the inter-factor correlation matrix as Φ = T -1 T -1 ́(7)
Illustrative example
The Statistical Anxiety Scale (SAS; Vigil-Colet, Lorenzo-Seva and Condon, 2008) is a measure of anxiety towards statistics that assesses three related dimensions of anxiety: Examination anxiety (EX; 8 items), Asking for help anxiety (AH; 8 items) and Interpretation anxiety (IN; 8 items). All 24 items are positively worded and use a five-point Likert response format, ranging from «no anxiety» (1) to «considerable anxiety» (5). The SAS was administered to a sample of 384 undergraduate students.
As the distributions were generally skewed, the item scores were treated as ordered-categorical variables, and we chose to compute the factor analysis on the basis of the polychoric inter-item correlations. This model is an alternative parameterization of the multidimensional IRT-graded response model (see Ferrando & Lorenzo-Seva, 2013).
The inter-item correlation matrix had good sample adequacy (KMO = .930; 95% confidence interval = .928 and .935), and the Optimal Implementation of Parallel Analysis (Timmerman & Lorenzo-Seva, 2011) suggested that three factors should be extracted. Next, a factor solution was fitted using Robust Factor Analysis based on the Diagonally Weighted Least Squares (DWLS) criterion as implemented in the FACTOR program (Ferrando & Lorenzo-Seva, 2017). Goodness-of-fit levels were acceptable: RMSEA = .090 (95% confidence interval = .0424 and .100), CFI = .981 (95% confidence interval = .968 and .995) and WRMR = 0.071 (95% confidence interval = .064 and .075).
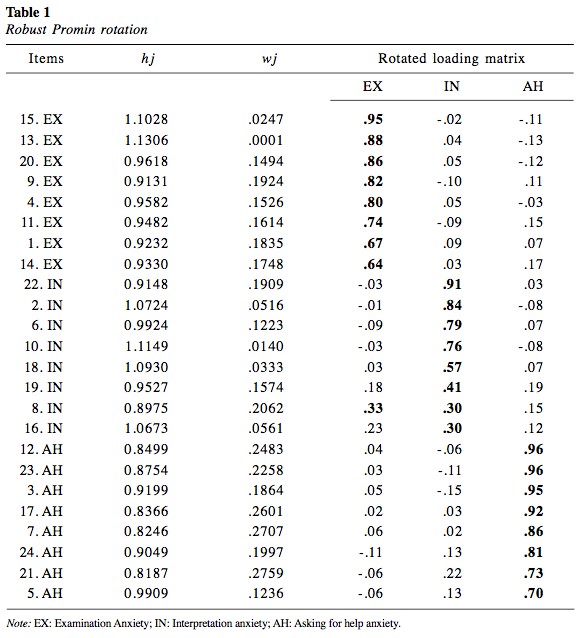
We computed the asymptotic variance/covariance matrix and observed that the variance values ranged between 0.15 (for the correlation of the pair of items 7 and 17) and 1.54 (for the correlation of the pair of items 10 and 13). The first column in Table 1 shows the averages of the 23 diagonal values for each item ( h j ). Interestingly, the items that were expected to measure Interpretation anxiety (IN) were the ones that generally produced the least stable correlations (i.e., correlations with the largest variances), while the items expected to measure Asking for help anxiety (EX) were the ones that produced the most stable correlations. So, it seems that the stability of the correlations was to some extent affected by the latent variables involved in the analysis. The second column in Table 1 shows the corresponding robust weights (wj). As can be observed, the item that produced the least stable set of correlations (item 13, which measures Examination anxiety) was given a weight of .0001, whereas the item that produced the most stable set of correlations (item 21, which measures Asking for help anxiety) was given a weight of .2759. None of the items was given a weight close to 1 because they all produced correlations with a considerable amount of sampling error. The last three columns in Table 1 show the rotated loading matrix after Robust Promin rotation. As can be observed, it is quite simple. Only a few items, like item 8 («Trying to understand a mathematical demonstration») related to Interpretation anxiety , had a complex structure. The value of the loading simplicity index (Lorenzo-Seva, 2003) was 0.655. Finally, the inter-factor correlation ranged between .35 and .52.
Robust Promin does not only focus on factor simplicity. It converges to a rotated solution that is assumed (a) to maximize factor simplicity, and (b) to be stable. This assumption implies that the rotated loading matrices obtained in different samples are more stable than the ones obtained with other rotation criteria. To determine whether this is so, we randomly split the sample into two halves, and replicated the same factor analysis in the subsamples using the same specifications as in the whole sample. For purposes of comparison, we rotated the loadings matrix obtained in each subsample using both Robust Promin and Promin. Table 2 shows the congruence and the Root Mean Square Residual (RMSR) values between subsamples. As can be observed, Robust Promin produced the most similar rotated solutions. In terms of congruence, Promin showed a congruence value that was slightly under the threshold of .95, which suggests that the rotated solutions may not have a perfectly identical interpretation in each subsample (Lorenzo-Seva & ten Berge, 2006). Finally, we repeated this last analysis 1,000 times, and observed that Robust Promin produced the most similar rotated solutions 68.9% of the times.
Discussion
The purpose of the present article was to present a robust modification of a well-known oblique rotation procedure, which is expected to lead to more stable across-sample solutions, and to maintain the simplicity and interpretability of the original Promin. As with weighted robust schemas in the extraction stage of factor analysis, Robust Promin is expected to be particularly advantageous when the sampling errors of the bivariate correlations are considerably different and these errors can be estimated with reasonable accuracy. Different sampling errors are more likely to occur if the input correlations are tetrachoric and polychoric, because in this case the correlation matrix is estimated not jointly but pairwise. The empirical example, which uses this type of correlation, shows that the asymptotic variances (and, therefore, the proposed weights) can vary considerably. It is also noteworthy that, with a sample size of only 384 respondents, the sampling errors are accurate enough to reveal the potential advantages of the method.
We have tested our diagonally-weighted factor rotation with Promin in order to propose Robust Promin. However, the same robust weighting scheme can be applied to other rotation methods that accept this sort of strategy. Some of the rotation methods for which our weighted schema are applicable are Weighted Varimax (Cureton & Mulaik, 1975) and Weighted Oblimin (Lorenzo-Seva, 2000), which would become Robust Varimax and Robust Oblimin when used with our approach.
Our experience suggests that proposals such as the present one can only be applied in practice when they are implemented in user-friendly and readily-available software. In this respect, the procedure proposed herein has been implemented in the 10.9 version of the FACTOR program (Ferrando & Lorenzo-Seva, 2017). In order to compute a diagonally weighted factor rotation with FACTOR, the user has to select (1) the robust factor analysis option, and (2) one of these three rotation methods: Promin, Weighted Varimax or Weighted Oblimin. The output of the program informs the researcher that a robust rotation has been computed.
Conflict of interest
The authors declare that there is no conflict of interest to be submitted to evaluation.
Acknowledgments
This project has been made possible by the support of the Ministerio de Economía, Industria y Competitividad , the Agencia Estatal de Investigación (AEI) and the European Regional Development Fund (ERDF) (PSI2017-82307-P).
Author contributions
ULS: conception and design of the study, interpretation of data and final revision of the manuscript.
PJF: discussion and final revision of the manuscript.
Para citar este artículo:
Lorenzo-Seva, U., & Ferrando, P. J. (2019). Robust Promin: a method for diagonally weighted factor rotation. Liberabit, 25(1), 99-106. doi: https://doi.org/10.24265/liberabit.2019.v25n1.08
Referencias
Browne, M. W. (1972). Oblique rotation to a partially specified target. British Journal of Mathematical and Statistical Psychology, 25, 207-212.
Browne, M. W. (2001). An overview of analytic rotation in exploratory factor analysis. Multivariate behavioral research, 36, 111-150.
Cureton, E. E., & Mulaik, S. (1975). The weighted varimax rotation and the promax rotation. Psychometrika, 40, 183-195.
Ferrando, P. J., & Lorenzo-Seva, U. (2013). Unrestricted item factor analysis and some relations with item response theory. Technical Report. Department of Psychology, Universitat Rovira i Virgili, Tarragona. Recuperado de http://psico.fcep.urv.es/utilitats/factor [ Links ]
Ferrando, P. J., & Lorenzo-Seva, U. (2014). El análisis factorial exploratorio de los ítems: algunas consideraciones adicionales. Anales de psicología, 30, 1170-1175.
Ferrando, P. J., & Lorenzo-Seva, U. (2017). Program FACTOR at 10: origins, development and future directions. Psicothema, 29, 236-240.
Hendrickson, A. E., & White, P. O. (1964). PROMAX: a quick method for rotation to oblique simple structure. British Journal of Statistical Psychology, 17, 65-70.
Kaiser, H. F. (1958). The varimax criterion for analytic rotation in factor analysis. Psychometrika, 23, 187- 200.
Kiers, H. A. L. (1994). Simplimax: oblique rotation to an optimal target with simple structure. Psychometrika, 59, 567-579.
Lorenzo-Seva, U. (1999). Promin: A method for oblique factor rotation. Multivariate Behavioral Research, 34, 347-365.
Lorenzo-Seva, U. (2000). The weighted oblimin rotation. Psychometrika, 65, 301-318.
Lorenzo-Seva, U. (2003). A factor simplicity index. Psychometrika, 6, 49-60.
Lorenzo-Seva, U., & Ten Berge, J. M. (2006). Tucker’s congruence coefficient as a meaningful index of factor similarity. Methodology, 2, 57-64.
Mosier, C. I. (1939). Determining a simple structure when loadings for certain tests are known. Psychometrika, 4, 149-162.
Schönemann, P. H., & Wang, M. M. (1972). Some new results on factor indeterminacy. Psychometrika, 37(1), 61-91. [ Links ]
Thurstone, L. L. (1947). Multiple Factor Analysis. Chicago: University of Chicago Press. [ Links ]
Timmerman, M. E., & Lorenzo-Seva, U. (2011). Dimensionality assessment of ordered polytomous items with parallel analysis. Psychological methods, 16, 209-220.
Vigil-Colet, A., Lorenzo-Seva, U., & Condon, L. (2008). Development and validation of the statistical anxiety scale. Psicothema, 20, 174-180.
Urbano Lorenzo-Seva
Department of Psychology, Faculty of Education Sciences and Psychology, Universitat Rovira i Virgili (Tarragona, Spain)
Doctor in Psychology and university professor. His work focuses on the proposal of methodological advances in the field of psyc hometrics.
ORCID: http://orcid.org/0000-0001-5369-3099
Correspondent author: urbano.lorenzo@urv.cat
Pere J. Ferrando
Department of Psychology, Faculty of Education Sciences and Psychology, Universitat Rovira i Virgili (Tarragona, Spain)
Doctor in Psychology and university professor. His work focuses on the proposal of methodological advances in the field of psyc hometrics.
ORCID: http://orcid.org/0000-0002-3133-5466
Este es un artículo Open Access bajo la licencia Creative Common (Atribución-NoComercial-CompartirIgual 4.0)
Recibido: January 9th, 2019
Aceptado: April 12th , 2019