Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Sociedad Química del Perú
Print version ISSN 1810-634X
Rev. Soc. Quím. Perú vol.81 no.3 Lima July/set. 2015
TRABAJO ORIGINAL
Computational study on second-order nonlinear optical properties of donor-acceptor substituted copper phthalocyanines
Estudio commputacional de las propiedades ópticas no lineales de segundo orden en ftalocianinas de cobre substituidas con ligandos donador-aceptor
Jean P. Inchaustegui1, Rodolfo Pumachagua1
1 Universidad Nacional Federico Villarreal, Facultad de Ciencias Naturales y Matemáticas, Laboratorio de Química Teórica, Jr. Chepén s/n (El Agustino) Perú. rpumachagua@yahoo.es
ABSTRACT
The second-order nonlinear optical properties (NLO) of a set of copper phthalocyanines have been studied based on density functional theory calculations. Our calculations show that they possess high value NLO properties. The first hyperpolarizabilities can be enhanced by position and number of donor-acceptor substituents along the phthalocyanine core.
Keywords: Phthalocyanine, hyperpolarizability, DFT.
RESUMEN
Las propiedades ópticas no lineales (NLO) de un grupo de ftalocianinas de cobre han sido estudiadas basadas en cálculos por teoría del funcional de la densidad. Nuestros cálculos muestran que éstas poseen altos valores en propiedades en NLO. La primera hiperpolarizabilidad puede ser mejorada por la posición y el número de sustituyentes donador-aceptor a lo largo del núcleo de ftalocianina.
Palabras clave: Ftalocianinas, hiperpolarizabilidad, DFT.
INTRODUCTION
In the field of nonlinear optics, organic materials on delocalized π-electron systems have attracted a great deal research interest in particular phthalocyanines1.
The family of phthalocyanines (Pcs) are based on 2-dimensional aromatic macrocycles that contain delocalized 18 π-electron clouds which exhibit a large number of unique properties, such as dying, molecular electronics and in the near future as a source of storage in quantum computing.
The rational design of new organic materials for nonlinear optics (NLO) represents a relevant and expanding topic that is reaching maturity because of their potential application in optoelectronics, particularly for the development of optical communications and computing technologies.
Metal phthalocyanines (MPcs) are planar fourfold-symmetry molecules characterized by a common electronic structure of the ligand independent from the metal in the center.
In recent years there has been a growing interest in the search for materials with large macroscopic second-order nonlinearities because of their practical utility as frequency doublers, frequency converters and electro-optic modulators. In order to optimize these effects, highly efficient materials have to be engineered. Second-order NLO effects are usually observed from noncentrosymmetric materials which are built up, for example, by incorporating donor-acceptor substituted organic molecules that have nonvanishing molecular hyperpolarizability. Thus, molecular engineering of one-dimensional (1-D) chromophores has been particularly active, leading to push-pull derivatives displaying huge first-order hyperpolarizabilities.
In accordance with their electronic structure, phthalocyanines present intense bands at the visible (Q band) and UV (B or Soret band) spectral regions that mostly determine the NLO response, for our purposes the first excited states are the most relevant which are established at the Q band. The Q band corresponds to transitions to the lowest excited state orbitals (eg) from the highest occupied orbital (au). The exact position of these bands depends on the particular structure, metal complexation and peripheral substituents2.
COMPUTATIONAL DETAILS
Calculations of geometry optimization, excited states properties, dipolar moment, polarizability and first hyperpolarizabilities were run using GAUSSIAN 09 program3. Molecular geometries were optimized with various DFT exchange correlation functionals such as B3LYP, HSE, MPW1PW91, CAM-B3LYP, TPSS and PBE. We have used the atom-centered split valence with polarization functions 6-31G(d, p) for C, H, O and N; and the LANL2DZ basis set with effective core potential (ECP) for electrons near the nuclei for the copper atom. Energetics of excited states were calculated using time dependent (TD) DFT with functionals mentioned above and also the 6-31G(d, p) basis set with LANL2DZ basis set on copper atom4-6.
Finite field method7, 8 has been widely used for computing the first hyperpolarizability β and the second hyperpolarizability γ. When a molecule is perturbed with a static electric field (F), the energy (E) of the molecule is expressed by the following equation:
E=E0–μiFi–(1/2)αijFiFj–(1/6)βijkFiFjFk–(1/24)γijklFiFjFkFl–… (I)
In this equation, E(0) is the energy of the molecules without an electric field, μi is the component of dipole moment vector, αis the polarizability tensor, β is the first hyperpolarizability tensor and γ is the second hyperpolarizability tensor; i, j, k are x, y and z components. The tensor components of the molecular dipole moment, polarizability, first and second hyperpolarizability are calculated by deriving the total energy with respect to the external electric field.
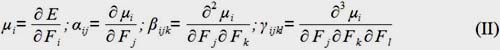
In this paper we use an electric field of 0.0010 Hartrees for determination of the static polarizability, first and second static hyperpolarizabilities.
For the dipolar moment, μ, and polarizability, α, have been calculated by using the following equations:
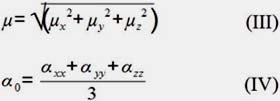
For the first hyperpolarizability, β, and second hyperpolarizability, γ, all components are calculated by the GAUSSIAN 09 program. The electron correlation effect has been considered by using DFT. We have employed PBE and HSE exchange correlation functional to calculate the nonlinear optical properties of the set of phthalocyanine derivatives for accurate predictions of the electronic excited states. The 6-31G(d, p) basis set is an appropriate choice for calculations of hyperpolarizability of molecules with atoms of more than 100 atoms hence it has been employed for the calculations in the current work.
RESULTS AND DISCUSSION
We have introduced four derivatives of copper phthalocyanine with donor-acceptor ligands studied in other works9-12. As shown in figure 1, four derivatives have been considered in this work; all of them have different positions of pair multiples of 4-nitrophenylethylvinyl as the acceptor group and cyanide as the donor group, those were denoted as 1, 2, 3 and 4, respectively.
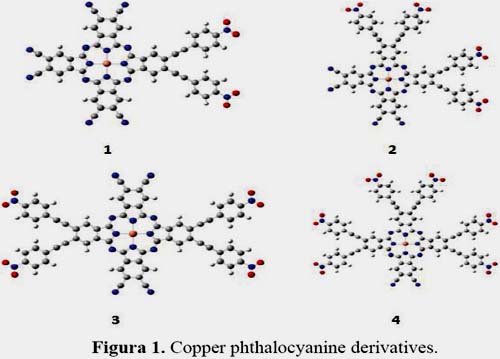
The copper atom is in the middle of the macromolecule, cyanide groups decrease with the numbers and nitrophenylethylvinyl increase.
For studying the phthalocyanine derivatives mentioned above we started calculating the optimized structure and energies of the orbitals of copper phthalocyanine; The Kohn-sham energy levels of CuPc were calculated with different exchange-correlation functionals: B3LYP, MPW1PW91, CAM-B3LYP, PBE, TPSS and HSE, spin unrestricted calculations were employed throughout and the geometry was optimized independently for each functional.
Copper phthalocyanine have a D4h symmetry in which 4 pyrrole rings are bridged assuming great electron delocalization due to the nature of the carbon-carbon and carbon-nitrogen bonds; All functionals described well the geometry with some slight considerations, GGA functionals yield slightly longer bond lengths comparing with the hybrids that yield shorter bonds, which is typical for this kind of organic molecules.
The data obtained from these calculations has been compared to the bibliography13, which corroborate previous studies, there is an underestimation in the spin splitting energy of the b1g orbital using GGA functionals due to self-interaction error around the copper center, this error is larger in localized orbitals, it is therefore that there is an alteration of the HOMO and LUMO levels, these functionals show that LUMO is well underestimated and this orbital is well organized using HSE screened hybrid functional which is the LUMO+1.
It is also noticed that hybrid functionals have the self-interaction error also; this problem is resolved by the inclusion of Fock exchange. This would explain the success of the hybrid functionals in predicting the energy levels of the occupied b1g orbitals of CuPc.
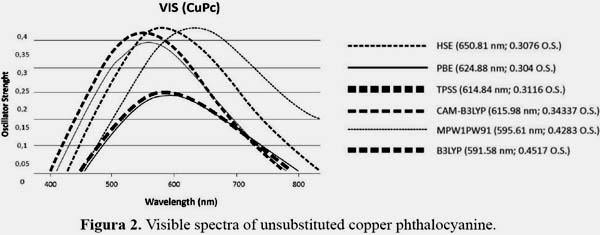
Time dependent Density Functional Theory studies were carried on using a set of functionals to evaluate the optical band gap which is shown in figure 2, according to experimental data in gas phase14, HSE is the more approximate to the experimental value of 656.2 nm (Q Band peak) with 650.81 nm, it has been also shown that this screened hybrid functional has been applied to organic and inorganic systems making a well-suitable functional to study electronic excitations in the phthalocyanine derivatives, PBE functional which is the second most accurate with a peak in 624.88 nm will be used to study the NLO also. Surprisingly CAM-B3LYP which is a long range functional does not show accurate data and even less B3LYP which is a not suitable functional for metal containing systems because they were not part of the data set against which B3LYP was parametrize. Hybrid functionals also lack accuracy for metal containing systems.
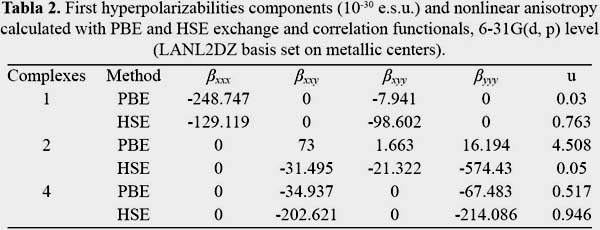
In order to know how the relation between structure and NLO properties is maintained, four structures have been studied as mentioned above, the second-order NLO properties of these copper phthalocyanine have been studies at HSE and PBE methods with 6-31G(d, p) basis set (LanL2DZ pseudopotential on the copper atom) in this work. The dipolar moment, polarizabilities and static first hyperpolarizabilities have been listed in table 1; most important tensor components have been listed in table 2. For complex 3 all values summed 0 with a little observation using HSE functional, the quasisymmetry of this system results in the vanishing of beta tensors.
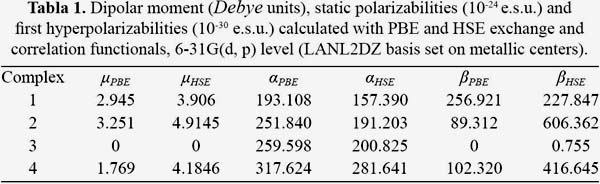
For the calculation of dipolar moment it can be observed that values evolve in the following order 3<4<1<2 those results are mainly observed by the non-symmetry of the molecules. For 3 the value is 0 due to its symmetry, and then it evolves as the molecules get more non-symmetric. Static values of polarizability evolve in the following order 1<2<3<4 due to the highly substitution pattern, 4 has maximum values, as more ligands are attached to the macrocycle, the molecule can be more polarized by an external field.
The introduction of PBE and HSE functionals greatly differs increasing the total hyperpolarizability values in all complexes, with the exception of 1, the ratio between HSE and PBE for 1 is 0.89, 6.79 for 2 and 4.07 for 4. Results show that there is no contribution of β zzz or z off diagonal tensors in the total hyperpolarizability, this is by the almost planar structure of the phthalocyanine derivatives. Contributions to the total hyperpolarizability are given by four tensors: β xxx, β yyy, βxyy and β xxy, the difference lies in the structures, in 1 β xxx and βxyy give the most important values, the long pi bridge from the acceptor group in the x axis enhances the contribution of these tensors, it has been shown that the ratio of the total static first hyperpolarizability between functionals is short but the mentioned tensors differs greatly, PBE gives higher results for the first component but not for the second one, HSE gives contrary results which can be explained by the long range exchange contribution. For 2 the difference is mainly addressed by the β yyy off diagonal tensor which is shown enhanced by the screened hybrid functional, the pi bridges are mainly the source of the high value which are 45 degrees inclined to the y axis. For 4 β yyy and β xxy gives the higher values, for both cases HSE enhances the first static hyperpolarizability, y axis gives a high value due to the acceptor-donor position.
For the studied systems exchange part of the functionals used can be regarded as an enhancement of the first static hyperpolarizability. The difference between ratios higher than 1 in most cases indicates the consideration of HSE as suitable for our studies.
In order to evaluate better the NLO character, the "in plane nonlinear anisotropy" concept u (depending on the ratio u =β xxy/βyyy) has been introduced in this work15. These values have been listed in table 2 and the results display considerable large values (from 0.517 to 4.508) which demonstrates that our structures possess good 2D second-order NLO properties. As shown in table 2 the calculated values are different and sensible to the donor-acceptor ligand axis bindings.
For good second order NLO responses of the studied systems, the properties of the most important excited states are studied. The most important for our purposes is the lowest excited states with large oscillator strength calculated with TDDFT. The oscillator strength, excited energy, transition dipole moment and orbital transitions have been listed in tables 3 and 4.
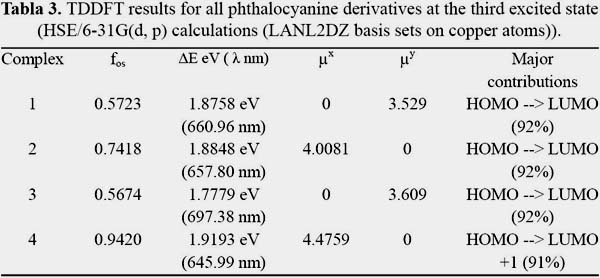
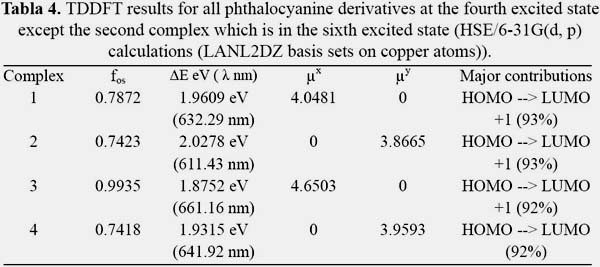
It is known that first hyperpolarizability is proportional to the oscillator strength and inverse proportional to the cube of excited state energy of the low-lying charge transfer excited state. It is shown in figures 3, 4, 5 and 6 the orbitals that feature the excited states charge transfer in complex 1, 2, 3 and 4. Only the x and y polarized transitions are allowed in all complexes, third and fourth excited states are associated with y and x transitions in 1 and 3 respectively, third and sixth are associated with x and y transitions in 2 respectively according to the transition dipole moment elements. For 1, 3 and 4 the Y-polarized transition arise from HOMO -> LUMO (92%) and X-polarized transitions from HOMO -> LUMO+1 (92%). For 2 the X-polarized transition arises from HOMO -> LUMO (92%) and Y-polarized transitions from HOMO -> LUMO+1 (92%).
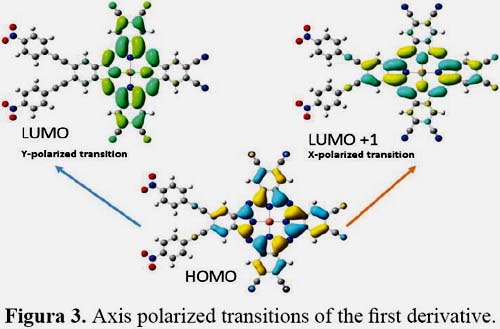
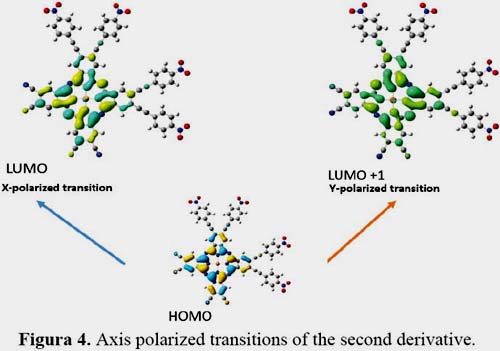
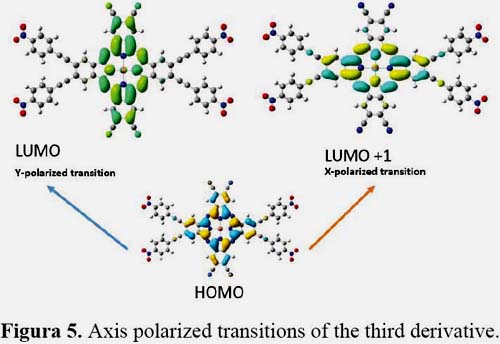
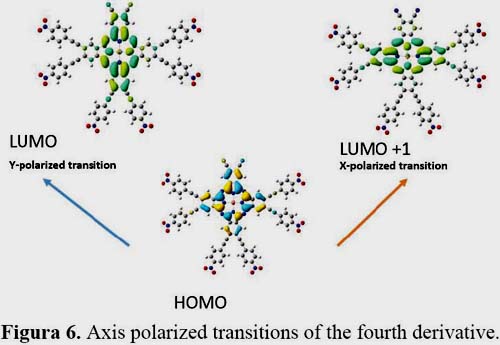
It can be found that HOMO is mainly polarized across donor ligands and phthalocyanine core, LUMO and LUMO+1 is mainly localized on the phthalocyanine core and the acceptor ligand, Thus these orbital transitions would generate charge transfer from electron donor to acceptor end and from phthalocyanine core to electron acceptor end. The phthalocyanine core not only acts as the p-conjugated bridge in all systems but also acts as the electron donor in this molecule.
CONCLUSIONS
DFT calculations have been performed on the second-order non-linear optical properties of a set of phthalocyanine donor-acceptor derivatives. Calculations show that second–order NLO properties of these molecules are sensitive to position of ligands along the phthalocyanine macrocyclic core. For 1, 2 and 4 have shown great first hyperpolarizability values that can be well used in second-order NLO applications. Our hyperpolarizability calculations show that position and number of donor-acceptor substituents have a strong contribution in nonlinear optical responses. TDDFT calculations show that the charge transfer corresponding to the most important excited states is mainly from electron donor to acceptor end and from phthalocyanine core to electron acceptor end.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the computational support of Andres Bello University for cover long time calculations and Catalina Pineda for her work on figures.
REFERENCES
1. J. S. Shirk, J. R. Lindle, F. J. Bartoli, C. A. Hoffman, Z. H. Kafafi & A. W. Snow, Off-resonant third-order optical nonlinearities of metal-Substituted phthalocyanines, Appl. Phys. Lett., 1989; 55: 1287-1288.
2. M. Blanchard-Desce, V. Alain, P. V. Bedworth, S. R. Marder, A. Fort, C. Runser, M. Barzoukas, S. Lebus & R. Wortmann, Large quadratic hyperpolarizabilities with donor–acceptor polyenes exhibiting optimum bond length alternation: Correlation between structure and hyperpolarizability, Chem. Eur. J., 1997; 3: 1091-1104.
3. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski & D.J. Fox, Gaussian09W, Revision A.02; Gaussian Inc., Wallingford CT, 2009.
4. P. J. Hay & W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg, J. Chem. Phys., 1985; 82: 270–283.
5. W. R. Wadt & P. J. Hay, Ab initio effective core potentials for molecular calculations. Potentials for main group elements Na to Bi, J. Chem. Phys., 1985; 82: 284–298.
6. P. J. Hay & W. R. Wadt, Ab initio effective core potentials for molecular calculations. Potentials for K to Au including the outermost core orbitals, J.Chem. Phys., 1985; 82: 299–310.
7. A. D. Buckingham, Permanent and induced molecular moments and long-range intermolecular forces, Adv. Chem. Phys., 1967; 12: 107–142.
8. A. D. Mclean & M. Yoshimine, Theory of molecular polarizabilities, J. Chem. Phys., 1967; 47: 1927–1935.
9. M. Tian, T. Wada, H. Kimura & H. Sasabe, Novel asymmetrically substituted metallophthalocyanines for nonlinear optics, Mol. Cryst. Liq. Cryst., 1997; 294: 271-274.
10. M. Tian, T. Wada, H. Kimura-Suda & H. Sasabe, Novel non-aggregated unsymmetrical metallopthalocyanines for second-order non-linear optics, J. Mater. Chem., 1997; 7: 861-863.
11. E. M. Maya, E. M. García-Frutos, P. Vásquez, T. Torres, G. Martín, G. Rojo, F. Agulló-López, R. H. González-Jonte, V. R. Ferro, J. M. Garcia de la Vega, I. Ledoux & J. Zyss. Novel push-pull phthalocyanines as targets for second-order nonlinear applications, J. Phys. Chem. A, 2003; 107: 2110–2117.
12. T. Torres, G. de la Torre & J. García-Ruiz, Synthesis of new push-pull unsymmetrically substituted styryl metallophthalocyanines: Targets for nonlinear optics. Eur. J. Org. Chem., 1999: 1999: 2323-2326.
13. N. Marom, O. Hod, G. E. Scuseria & L. Kroni, Electronic structure of copper phthalocyanine: A comparative density functional theory study, J. Chem. Phys., 2008; 128: 164107.
14. G. A. Kumar, G. Jose, V. Thomas, N. V. Unnikrishnan & V. P. N. Nampoori, NIR to UV absorption spectra and the optical constants of phthalocyanines in glassy medium, Spectrochimica Acta Part A, 2003; 59: 1-11.
15. S. Di Bella & I. Fragalá, Two-dimensional characteristics of the second-order nonlinear optical response in dipolar donor-acceptor coordinates complexes, New J. Chem., 2002; 26: 285-290.
Recibido el 06-08-2015
Aprobado el 25-08-2015