Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Journal of Economics, Finance and Administrative Science
versión impresa ISSN 2077-1886
Journal of Economics, Finance and Administrative Science v.15 n.28 Lima jun. 2010
Estimation of Discount Rates in Latin America: Empirical Evidence and Challenges*
Estimación de los ratios de descuento en Latinoamérica: Evidencia empírica y retos
Darcy Fuenzalida1; Samuel Mongrut2
1. Departmento de Industrias Universidad Federico Santa Maria, Chile. <darcy.fuenzalida@usm.cl>.
2. EGADE-ZC Instituto Tecnológico y de Estudios Superiores de Monterrey (ITESM) Campus Querétaro, Mexico. <smongrut@itesm.mx>.
Abstract
This paper compares the main proposals that have been made in order to estimate discount rates in emerging markets. Seven methods are used to estimate the cost of equity capital in the case of global well-diversified investors; two methods are used to estimate it in the case of imperfectly diversified local institutional investors; and one method is used to estimate the required return in the case of non-diversified entrepreneurs. Using the first nine methods, one estimates the costs of equity for all economic sectors in six Latin American emerging markets. Consistently with studies applied to other regions, a great deal of disparity is observed between the discount rates obtained across the different models, which implies that no model is better than the others. Likewise, the paper shows that Latin American markets are in a process of becoming more integrated with the world market because discount rates have decreased consistently during the first five-year period of the XXI Century. Finally, one identifies several challenges that have to be tackled to estimate discount rates and valuate investment opportunities in emerging markets.
Keywords: Discount rates, cost of equity, emerging markets.
Resumen
Este estudio compara las principales propuestas que se han dado para estimar las tasas de descuento en los mercados emergentes. Se han usado siete métodos para estimar el costo de capital propio en el caso de inversionistas globales bien diversificados; se aplicaron dos métodos para estimar dicho costo en caso de inversionistas corporativos locales imperfectamente diversificados; y se utilizó un método para estimar el retorno requerido en el caso de empresarios no diversificados. Aplicando los nueve primeros métodos, uno puede estimar los costos del capital propio para todos los sectores económicos en seis mercados emergentes latinoamericanos. Consistentes con estudios aplicados en otras regiones, se observó una gran disparidad entre las tasas de retorno obtenidas en los diferentes modelos, lo que implica que ningún modelo es mejor que el otro. De igual modo, el artículo demuestra que los mercados de Latinoamérica están en proceso de integración con el mercado mundial debido a que las tasas de descuento han decrecido sistemáticamente durante el primer lustro del siglo XXI. Finalmente, se identifican varios retos que deberán ser abordados para estimar las tasas de descuento y valorar las oportunidades de inversión en los mercados emergentes.
Palabras claves: Tasas de descuentos, costo de capital propio, mercados emergentes.
Introduction
When we wish to assess the value of a company or an investment project, it is not only necessary to have an estimation of the future cash flows, but also to have an estimation of the discount rate that represents the required return of the stockholders that are putting their money in the company or project. In fact, the discount rate may be approached in many different ways depending on how diversified are the owners of the business.
As a rule, in the literature of corporate finance it is normally assumed that these owners are none others than shareholders with a well diversified investment portfolio and, therefore, the discount rate could be understood as a cost of equity capital, which only depends on the market risk that is addressed by means of the well-known parameter beta. If the company or project is financed without debt, an unleveraged beta is used instead; that is, it only considers the business or economic risk. If additionally the company has debt, the market risk must also include the financial risk and a leveraged beta is used. Alternatively, it could also be possible to consider the required return by creditors too, in which case the discount rate is a weighted-average cost of capital.
The final objective is to estimate the value of the company or investment project as if were traded in the capitals market; in other words, we are looking for a market value. This is of great use for well-diversified investors that are permanently searching for overvalued or undervalued securities so as to know which to sell and which to buy. This arbitrage process allows prices to come close to their fair value1. However, in Latin American emerging markets, as well as in developed markets, there are local institutional investors (pension funds, insurance companies, mutual funds, among others) which do not hold a well-diversified investment portfolio for legal reasons or due to herding behavior2.
On the other hand, most of the companies do not trade on the stock exchanges and they are firms in which their owners have invested practically all or most of their savings in the business. Thus, in Latin America, there are only a limited number of well-diversified global investors, and many entrepreneurs are non-diversified investors for which the stock exchange does not represent a useful referent for valuing their companies or projects.
Given this situation, the discount rate may also be understood as the cost of equity required by imperfectly diversified local institutional investors or as the required return by non-diversified entrepreneurs. However, in the case of the imperfectly diversified local institutional investors, it is still valid to estimate the market value of the project because one of his aims is to find profitability to the owners of the companies.
In the case of the non-diversified entrepreneur, there is no need to estimate the value of the project as if it were traded on the stock exchange unless there is a desire to sell the business to well-diversified global investors or to institutional investors. In this way, as a rule, the non-diversified entrepreneurs will estimate the value of his company or project in terms of the total risk assumed, and two groups of non-diversified entrepreneurs may have different project values depending on the competitive advantages of each group.
Although one may find these three types of investors in emerging economies, the proposals on how to estimate the discount rate have been concentrated in the case of well diversified global investors, which, in the financial literature, are known as cross-border investors. The proposals have been few, and not theoretically sound, in the case of imperfectly diversified institutional investors, and almost non-existent in the case of non-diversified entrepreneurs (Mongrut & Ramirez, 2006).
In this paper, the aim is to compare the performance of the main models that have been proposed in the financial literature to estimate the discount rate in the case of well diversified global investors, imperfectly diversified investors and non-diversified entrepreneurs in six Latin American stock exchange markets that are considered as emerging by the International Finance Corporation (IFC)3: Argentina, Brazil, Colombia, Chile, Mexico and Peru. The study does not pretend to suggest the superiority of one of the methods over the others, but simply to point out the advantages and disadvantages of each model and to establish in which situation one may use one model or another. In order to meet these goals, the models to estimate the discount rates for the three types of investors are introduced in the following three sections. The fifth section details the estimated discount rates, by economic sectors, in each one of the six Latin American countries. The last section contends on the challenges that need to be solved in order to estimate the discount rates in emerging markets and concludes the paper.
MODELS TO ESTIMATE THE COST OF CAPITAL IN THE CASE OF WELL DIVERSIFIED INVESTORS
During the last ten years, a series of proposals have been put forward to estimate the cost of equity capital for well diversified investors that wish to invest in emerging markets. A compilation of these models may be found in Pereiro and Galli (2000), Pereiro (2001), Harvey (2001) and Fornero (2002). The proposals could be divided into three groups according to the degree of financial integration of the emerging market with the world: complete segmentation, total integration and partial integration. Two markets are fully integrated when the expected return of two assets with similar risks is the same; if there is a difference, this is due to differences in transaction costs. This also implies that local investors are free to invest abroad and foreign investors are free to invest in the domestic market (Harvey, 2001).
According to this definition, the Capital Asset Pricing Model (CAPM), as originally developed by Sharpe (1964), Lintner (1965) and Mossin (1966), is a domestic model that assumes complete segmentation. In the other extreme case, the global or world CAPM is found, a model that assumes complete integration. Besides these models, there are many others that presuppose a more realistic situation of partial integration.
Among the models of partial integration, the following ones have been chosen because they are either theoretically sound (given their assumptions) or popular among practitioners: the Mariscal and Lees or Goldman Sachs model, the Lessards model, the D-CAPM model, the Hybrid model and the Damodarans model. The differences among these models of partial integration lie on where one could include a critical variable named country risk, which is defined as the risk that private and public companies or agencies default upon their obligations (Fuenzalida, Mongrut & Nash, 2005). In this sense, the Goldman Sachs model assumes that the country risk could be included in the risk-free rate; the Lessards model and the D-CAPM assumes that it can be included in the market systematic risk (beta); the hybrid model and the Damodarans model assume that it can be included in the market risk premium. Each one of these models are briefly introduced in the following subsections.
The local CAPM
The local CAPM states that in conditions of equilibrium, the expected cost of equity is equal to (Sharpe, 1964):

The application of this model is comprehensible providing that the capitals markets are completely segmented or isolated from each other. However, this assumption does not hold. Furthermore, as Mongrut (2007) points out, the critical parameter to be estimated in equation (1) is the market risk premium. Unfortunately, the market risk premium is usually negative in emerging markets due to the markets high volatility with negative skewness, as well as the short time span for historical financial series. Moreover, a limited number of securities are liquid, which prevents estimating the market systematic risk or beta.
Global CAPM
The global or world CAPM was originally proposed by Solnik (1974). Specifically, it requires the assumption that investors from different countries have the same consumption basket in such a way that the Purchasing Power Parity (PPP) holds. Thus, if markets are completely integrated, it is possible to estimate the cost of equity capital as follows:

The global risk-free rate usually is approximated using the ten years return series the United States of America (US) Treasury Bonds.
If the US market is highly correlated with the global market, the above formula may be restated as follows:
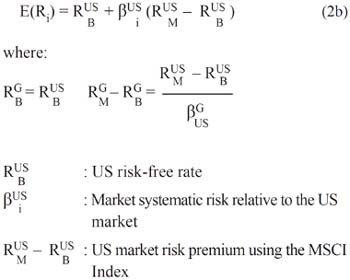
However, there usually are deviations relative to the PPP, either due to differences in the consumption tastes between the groups of individuals in different countries or to differences in prices of the goods to what they have access (Adler & Dumas, 1983). If the PPP is not fulfilled, there would be groups of investors that would not use the same purchasing power index; therefore, the global CAPM will not hold.
The Goldman Sachs model
One of the first models found in the literature of partial integration to estimate the cost of equity capital in emerging markets was the one suggested by Mariscal and Lee (1993). This model is also named the Goldman Sachs model because both authors proposed this model while they were working for that company. They suggested that the cost of equity capital could be estimated in the following way:

Note that in this specification the CAPM is estimated relative to the US Standard & Poors index and that to the sovereign risk is added to the risk-free rate. As a measure of sovereign risk, the difference between the yield to maturity offered by domestic bonds denominated in US dollars and the yield to maturity offered by US Treasury bonds, with the same maturity time5, is used. Despite its simplicity and popularity among practitioners, this model has a number of problems (Harvey, 2001):
-
A sovereign yield spread (debt) is being added to an equity risk premium. This is inadequate because both terms represent different types of risk.
-
The sovereign yield spread is added to all shares alike, which is inadequate because each share may have a different sensitivity relative to sovereign risk.
-
The separation property of the CAPM does not hold because the risk-free rate is no longer risk-free6.
Lessards hierarchical model
In 1996, Lessard suggested that the adjustment for country risk could be made on the stock beta and not in the risk-free rate as in the previous approach. In order to gain more insight into this proposal, it assumes that it is possible to state a linear relationship between the stock returns of the US and those of the emerging market (EM) through their respective indexes:
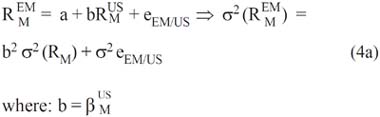
The stock beta relative to the emerging market is given by the following expression:
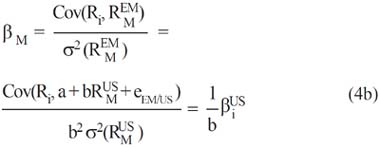
The latter expression may be written as:
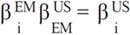
If, and only if, the following conditions are met:
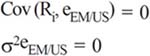
In other words, the return of the security should be independent of the estimation errors for the return of the emerging market and the latter should be well explained by the returns of the US market. With these assumptions in mind, the equation (2b) could be written in the following way (Lessard, 1996):
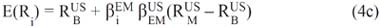
However, nothing warrants that both assumptions could hold, hence the following relationships between betas will not be fulfilled7:

Though this would be a serious limitation, Lessards model enjoys some popularity among investment analysts because it increases the beta of the security with respect to that of the emerging market adjusting it by the beta of the emerging market relative to the US. As in the case of the Local CAPM and the Global CAPM, they usually resort to Morgan Stanley Capital International (MSCI) indexes to make the calculations comparable.
The D-CAPM model
Estrada (2002) takes up the observation made by Markowitz (1959) three decades before: the investors in emerging markets pay more attention to the risk of loss than to the potential gain which they may obtain. In this sense, using a measure of total systematic risk as the stock beta is not adequate because it does not capture the real concern of the investors in these markets.
In this sense, Estrada (2002) suggested a variant of the CAPM, which he called D-CAPM (Downside Risk - CAPM). The D-CAPM uses the Global CAPM model and only substitutes the estimation of the securitys beta for the estimation of its D-Beta (Downside Beta) using the concepts of semi-standard deviation and cosemivariance. The Downside Beta is estimated as follows:

Hence, the cost of equity is established as a version of equation (2a):
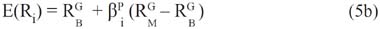
Even though the D-CAPM yields estimates of the cost of equity that are higher than those obtained with the Global CAPM, these still have a low magnitude for emerging markets. Despite this, the model is theoretically sound and represents a good alternative to the Local CAPM and Global CAPM. Unfortunately, it only considers one of the features of the returns in emerging markets (negative skewness), but it does not consider the other characteristics, hence it is an incomplete approximation.
The hybrid model
If emerging markets are partially integrated, then the important question is how this situation of partial integration can be formalized in a model of asset valuation. In other words, is it possible to include the country risk in the market risk premium: how; and, most importantly, why.
Bodnar, Dumas and Marston (2003) contend that a situation of partial integration may be stated in an additive way, meaning that local and global factors are important to pricing securities in emerging markets:

Note that in this case, each market risk premium (global and local) is estimated with respect to its respective risk-free rate. The world MSCI index is used to calculate the world premium and the local emerging market MSCI is used to estimate the local premium for market risk.
The estimation of the betas is carried out using a multiple regression model:
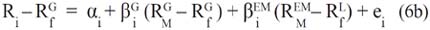
If the hypothesis that local factors are more important than global factors in estimating the cost of equity capital and considering that the market risk premium in Latin American emerging markets is usually negative, then a negative cost of capital ought to be obtained. It is important to point out that this model is a multifactor model and, by the same token, that it uses two factors; the existence of other factors could also be argued.
According to Estrada and Serra (2005), there is hardly any evidence that a set of three families of variables can explain the differences between the returns of the portfolios composed by securities from emerging markets. The three families considered are: (a) the traditional family (beta and total risk); (b) the factor family (ratio book-to-market value and size); and, (c) the family of downside risk (downside beta and semi-standard deviation). Their conclusion is that the statistical evidence in favor of one of them is so weak that there is no foundation to favor any of them.
Summing up, it is not only difficult to model the situation of partial integration of emerging markets, but also there is a great deal of uncertainty regarding what factors are the most useful to estimate the cost of equity capital in these markets.
Damodarans model
If the emerging markets are partially integrated and if the specification given by the equation (6a) is possible, one of the great problems to be faced is that the market risk premium in emerging markets is usually negative; so, the cost of equity instead of increasing will decrease. Damodaran (2002a) has suggested adding up the country risk premium to the market risk premium of a mature market, like the US. In order to understand his argument, let us assume that, under conditions of financial stability, the expected reward-to-variability ratio (RTV) in the local bond emerging market is equal to the RTV ratio in the local equity emerging market, so there are substitutes:
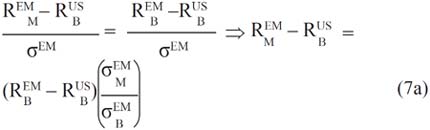
Note that one is working with US dollars returns and financial stability at a certain level of country risk for local bond and equity markets, hence: 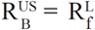
If one approximates the global market by the US market, and if equation (7a) and the previous condition are introduced in equation (6a), one obtains the general model proposed by Damodaran (2002a) to estimate the cost of equity capital:
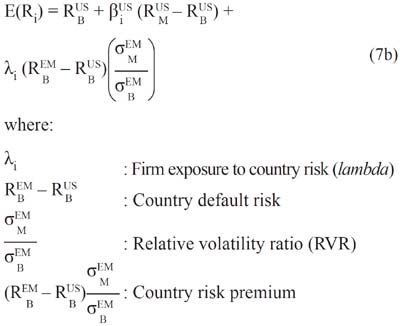
Note that the second slope (β) of the equation (6a) has been changed to a new slope denominated lambda (λ) in equation (7b). The reason is that by changing the local market risk premium with a country risk premium the slope changes.
This specification is useful because it directly avoids estimating the local market risk premium - the most important parameter in the estimation -, which displays the greatest estimation error (Ferson & Locke, 1998). Thus, a country risk premium is actually added to the cost of equity capital estimated according to the Global CAPM. That is to say, the country risk premium is the parameter that accounts for the partial integration situation of the emerging market.
Damodaran (2003) suggests two ways to estimate the security exposure to country risk (λ): (1) the resulting slope in the regression between the returns of the security with respect to the returns of bonds issued by the emerging country that are not guarantee; and, (2) the ratio between the percentage of revenues (I) that the company (j) obtains from the local market (L) divided by the percentage of income that companies obtain on average from the local market (P):
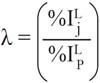
Despite these suggestions, the estimation of lambdas and the RVR ratio in emerging markets face several problems: the information with respect to the origin of revenues is private in many cases. Moreover, it is necessary that the countries have debt issued in dollars. Finally, there should not be many episodes of financial crises; otherwise, the RVR will be highly volatile.
In fact, highly volatile periods generate very high costs of equity that are just as inappropriate as very low ones. One way of overcoming this problem is to follow the suggestion that Walker (2003) has called the Damodarans conjecture that assumes a RVR equal to 1.50. Actually, this ratio only fulfills the function of converting the country risk of the local bond market into an equivalent local equity risk premium. Walker (2003) suggests that in order to test Damodarans conjecture the following model could be estimated:

If Damodarans conjecture is to be valid, the sensitivity of the returns of the security with respect to sovereign yield spread should not be statistically different from 1.5 since it is the relative volatility ratio (RVR). If the constant is not significantly different from zero then one has been built a mimicking portfolio of the securitys return by investing βusi in the US portfolio, in the sovereign bonds of the emerging market and the difference (1 –βUSi –βB,MEi ) in the US Treasury Bonds (Walker, 2003).
MODELS FOR ESTIMATING THE COST OF EQUITY IN THE CASE OF IMPERFECTLY DIVERSIFIED INSTITUTIONAL INVESTORS
The literature has neither established an adequate way to measure the degree of diversification of an investor portfolio nor whether a situation of imperfect diversification should bear a market price. Damodaran (2002b) has suggested that the situation of imperfect diversification should increase the cost of capital, so it must bear a market price and one way to take account of it is by means of the adjusted or total beta:

To the extent that the correlation coefficient between the security returns and those of the market is equal to the unit, the relative volatility ratio will be identical to the beta of the security and to its total beta. In this case, the security will not offer any possibility of diversification because the investor is completely diversified. To the extent that the correlation coefficient is lower than the unit, the investor will be less diversified, and there will be a market price for not being well-diversified; then, the total or adjusted beta will be higher than the normal beta.
In the literature, three models have been proposed to adjust for imperfect diversification: (a) the model of Godfrey and Espinosa (1996); (b) the Estradas model (2000); and (c) the Damodarans model (2002b). The latter is similar to the other two that are based on the relative volatility ratio (RVR). For this reason, this study only considers the first two models.
Godfrey and Espinosas model
Godfrey and Espinosa (1996) suggested using the so-called adjusted beta or total beta, which, as observed, is none other than the relative volatility ratio (RVR). The model is as follows:
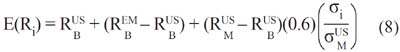
These authors accounted for the country risk in the risk-free rate. According to Erb, Harvey and Viskanta (1995), the volatility of the emerging stock markets explains at least 40% of the variation in the credit quality. Then, a way to avoid taking twice the country risk is to adjust ad hoc downwards the relative volatility ratio by 40%. This is the reason why the authors use an ad hoc correlation coefficient equal to 0.60. In this case, they are in fact lowering the beta, but their approach is considered as being an adjusted beta because they use ad hoc adjustments of it.
Finally, note that the sovereign yield spread is added to the risk-free rate without making any assumption. Furthermore, there is no theoretical foundation to make an arbitrary adjustment in the correlation coefficient. Despite these problems, this model gained some attention from practitioners at the end of the nineties.
Estradas model
In line with the argument that the downside risk is truly relevant for investors in emerging markets, Estrada (2000, 2001) proposes the following general expression to estimate the cost of equity using the relative volatility ratio (RVR):

In turn, the RVR may take one of the following specifications:
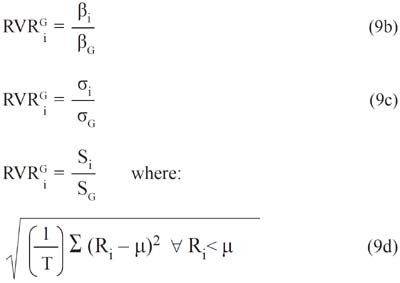
The three specifications may be replaced in the equation (9a) to obtain one of the three versions of Estradas model8. Despite this, it is important to point out that none of the three specifications has a sound theoretical foundation, and that they are ad hoc adjustments to estimate the cost of equity capital.
ESTIMATION OF REQUIRED RETURNS FOR NON-DIVERSIFIED ENTREPRENEURS
As Mongrut and Fuenzalida (2007) state, more than 95% of all the companies in Latin America are micro, small or medium companies. Thus, it is highly unlikely to find well-diversified investors among the owners; therefore, all the models studied above are inadequate. This is due to the fact that these investors are exposed to their investment total risk and not only to the systematic market risk.
Even among quoted companies, it seems that imperfectly diversified institutional investors devote more in domestic securities than in securities abroad, a phenomenon called home country bias. In this sense, one should expect that local factors influence more in the security pricing rather than global factors.
In fact, Koedijk, Kool, Schotman and Van Dijk (2002) carried out a study in order to find out whether local and global factors affected the estimation of the cost of equity capital. They concluded that the local factors accounted for a substantial part of the estimated cost of capital, which they attributed to the so-called home country bias.
More recently, Koedijk and Van Dijk (2004) have verified, from a sample of nine industrialized countries, that in the case of approximately 95% of this sample of 3,300 stocks the estimate of the cost of equity capital with the local CAPM does not differ significantly from that obtained with the International Capital Asset Pricing Model (ICAPM) that includes a premium for exchange rate risk. This indicates once again that local factors are sufficient to estimate the cost of equity capital in some developed markets.
Furthermore, Harvey (2000) showed that historical returns in emerging markets are explained by the total volatility of these returns, suggesting that total risk is one of the most important factors. Stevenson (2001), in turn, has shown that, if investors want to have an improvement in the performance of their international investment portfolio in emerging markets, it is useful to consider measures of downside risk in building such portfolio.
The relationship between total risk and returns is given not only in historical terms, but also this relationship persists with ex ante estimations of risk and profitability. Mishra and OBrien (2005) examined the relationship between ex ante estimates of cost of capital and total risk (volatility of returns) for a sample of securities in emerging markets during the period 1990-2000. They found that total risk was the most significant factor in explaining the ex ante estimations of cost of capital.
In a consistent way with this study, Harvey (2004) saw a significant relationship between the different components of country risk, estimated ex ante and the implicit estimation of the cost of capital in emerging markets9. This implies that not only total risk but also political, economic and financial risk - which are components of country risk - are associated to an ex ante estimation of the cost of capital. On the other hand, Erb, Harvey and Viskanta (1996a) have shown that these components are positively correlated to the measure of credit risk rating made by the Institutional Investor Magazine.
Twice a year, since 1979, this magazine publishes a Country Credit Rating (CCR) of each developed and emerging country, covering a total of 150 countries. To the extent that this CCR is closer to one hundred it means less credit risk for the country as a whole; and to the extent that it is closer to zero it indicates a greater credit risk. Erb, Harvey and Viskanta (1996b) have proposed the following model (EHV) to estimate the required return (based in the CCR) for the countries that are included in this credit risk ranking:

The two alpha parameters are estimated on the basis of the following cross-section and times series regression:
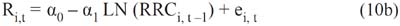
In this case, a cross-section time series regression analysis is performed between the series of the semi-annual market returns indexes for all countries (developed and emerging) against the natural logarithm of the CCR lagged one semester to avoid looking ahead bias. Once the required semi-annual return is estimated using equation (10a), the CCR from the contemporaneous semester is applied to estimate the forward looking required return. Finally, the equivalent annual figure is estimated for each country10.
A great advantage of this method is that it can estimate the forward looking required return for a country. Given that the number of countries that have a CCR is higher than the number of countries that have a stock exchange market, the model can be estimated with all the countries with CCR and capital market, and, then, substitute the corresponding CCR for a country in the equation (10a) without a capital market and obtain its corresponding required return.
Despite this advantage, the model also has some disadvantages; one of them is that the CCR is only developed twice a year by Institutional Investor. In this way, the rating exhibits little volatility, and the estimation of the model (10b) will have a low explanatory power (a low goodness of fit), even if the parameters obtained are statistically significant. A more serious disadvantage is that the model can only be applied to a country as a whole and not to an individual company. The CCR, which includes political, economic and financial risk, is expected to have a systematic component and a specific component. This implies that credit risk will not affect companies operating in the country in the same way and, therefore, required returns should be different for each company.
ESTIMATING DISCOUNT RATES IN LATIN AMERICAN EMERGING MARKETS
This section estimates the discount rates for the different economic sectors in six Latin American emerging markets: Argentina, Brazil, Colombia, Chile, Peru and Mexico. Venezuela was not included in the sample because it has very few liquid stocks. The following summarizes the result of seven models for estimating the cost of equity assuming global well-diversified investors, two models for estimating the cost of equity assuming imperfectly diversified institutional investors, and one model for non-diversified entrepreneurs.
Sample and methodology
We estimated costs of equity according to different models for six periods of five years: 1995-2000, 1996-2001, 1997-2002, 1998-2003, 1999-2004 and 2000-2005. We have avoided estimating the costs of equity for more recent periods because the goal is to find out what is the situation of Latin American markets at the beginning of the 21st Century.
One important filter for the data was liquidity. Table No. 1 shows the total number of liquid securities by country that had a stock market presence higher than 75% within each one of the periods of five years. Stock market presence is defined as the ratio between the days that the stock has traded divided by the total number of trading days at the stock exchange11.
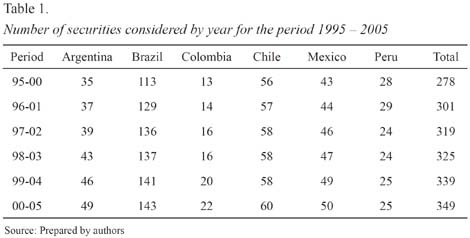
Thus, for the first period 278 securities were considered to estimate the cost of capital, whereas in the last period 349 securities were taken into account. It is worth mentioning that the number of liquid securities does not coincide with the number of different companies because sometimes there are two or three types liquid stocks attached to one company.
The next step was to estimate the cost of equity models for each liquid security using equations 1, 2a, 3, 4c, 5b, 6a, 7b, 8 and 9c. In the case of model 7b, the Damodarans conjecture was considered. The local risk-free rate was approximated using the shortest-term rate offered by the bill notes from the emerging markets Central Banks. In the case of the US, the return of the one-month bill notes was used. Due to the fact that the cost of equity at the end of every year was estimated, the risk-free rates values used to calculate the costs of equities were those from the end of each year.
With the exception of models 1 and 6a, all market risk premiums were estimated with respect to the US market, so the value of 5.5% was applied to compare this study with previous studies that used the same figure such as the ones of Stulz (1995), Lessard (1996), and Estrada (2000, 2001 and 2002). For models 1 and 6a, we used the average continuously compounded excess return of the MSCI local stock market index for the longest time-span12.
As it is standard in financial literature, the securities betas were calculated using linear regressions with monthly returns for the last five years. The estimations were updated each year using a rolling window of five years in a way that the variations in the cost of equity are due to variations in the securities betas through time. All the stock returns were continuously compounded returns and in US dollars.
Costs of equity in Latin American emerging markets
Tables A1 to A6 in the Appendix show the annual costs of equity for the different economic sectors in the six countries. To obtain these results, simple averages of the costs of equity of all the securities in the same sector within the same model were calculated. Also, the authors followed the industry classification given by Economatica.
In the case of globally well-diversified investors, under a completely integrated market and under a complete segmented market, the costs of equity were obtained through simple averages of the estimates by sectors using the Global CAPM and the Local CAPM models, respectively.
In the case of a partial integrated market, the costs of equity were estimated by averaging the results of the following models (Mariscal & Lee, 1993; Lessard, 1996, D-CAPM, & Damodaran, 2002, 2003)13. The results from the hybrid model were not considered to calculate the averages per sector because they were negative costs of equity for two markets (Argentina, Chile).
In the case of imperfectly diversified local institutional investors, the costs of equity were obtained by averaging the results of the Godfrey and Espinosas model and the Estradas model (2000, 2001)14. This procedure of averaging the resulting costs of equity through the different models per economic sector was proposed in the work of Fama and French (1997). These authors found that standard errors in the estimation of the Local CAPM and the Three-Factor Model of Fama and French (1993) could be higher than 3% on an annual basis, so one way to reduce these standard errors is by averaging the results from different models that assume the same degree of market integration15.
Table A1 to Table A6 may raise some observations. For instance, the estimated costs of equity for well-diversified investors under a total segmented market (Local CAPM) are extremely volatile, in many cases negative and in other cases excessively high such as in Argentina. This latter result could be explained because, under a situation of bear markets, emerging markets become more correlated with developed markets and, given the high volatility, it is not surprising to have high costs of equity estimations. However, if the crisis is more localized to a region, the low correlation between emerging market returns and developed market returns do not change and the costs of equity estimations tend to be small.
On the other hand, given the excessive volatility of Latin American emerging markets and the properties of their stock returns (negative skewness and excess of kurtosis), it is not surprising that in some cases there are negative estimations of the market risk premium and, consequently, of the costs of equity using the Local CAPM. Together, all these problems render the Local CAPM model useless for the estimation of the cost of equity in these markets.
In the case of complete integration, under either a regional contagion or financial markets stability, the estimation of the costs of equity are rather of low magnitude given the low correlation between emerging markets and developed markets. In other words, the estimated betas do not capture the complete systematic risk that a global investor faces when investing in Latin American emerging markets. In Chile, for example, there are a few sectors where the costs of equity are excessively volatile due to very high systematic risk estimations (betas).
When a situation of partial integration is considered, it can be seen that the costs of equity estimations are usually higher than the ones estimated under complete integration for all capital markets. However, the absolute magnitude of the estimated costs of equity is still quite low because they are on average in the neighborhood of 10%. This magnitude is counter intuitive because a global well-diversified investor probably will require a higher cost of equity to invest in Latin American markets.
Higher costs of equity are obtained using the models of imperfectly diversified institutional investors because, on average, they are higher than the costs of equity obtained in the case of partially integrated markets (with the exception of Brazil and Mexico). Unfortunately, the applied models lack sound theoretical foundation.
Note that all estimated costs of equity decrease across the six five-year periods for most of the economic sectors and in all countries (with the exception of the ones estimated using the Local CAPM). In other words, the cost of equity estimated at December 31st of the year 2000 decreased substantially when compared to the cost of capital estimated at October 31st of the year 2005. This fact indicates a process of financial integration with the world market.
Table A7 to Table A12 show the average statistical significance of the securities betas projected with each model by degree of investors diversification. Each beta was estimated with the continuous last sixty monthly compounded returns in dollars and adjusted by dividends within in each one of the following five periods: 1995-2000, 1996-2001, 1997-2002, 1998-2003, 1999-2004 y 2000-2005 16.
Table A7 shows that Local CAPM, on average, is the model that has a high proportion of significant betas at 95% confidence level in all countries: Argentina (86%), Brazil (90%), Colombia (77%), Chile (95%), Mexico (87%) and Peru (75%). This is consistent with the current literature that shows that local factors are more important than global factors to estimate the cost of equity. For instance, the betas significant proportion using the Global CAPM was Argentina (56%), Brazil (78%), Colombia (12%), Chile (75%), Mexico (79%), and Peru (40%). Note that this is a simple way to assess which country is more integrated than the other and the results are according to the intuition. Furthermore, it is possible to observe that in the case of Argentina the proportion of statistically significant betas decreases in the more recent periods, probably due to the Argentinean crisis, while the opposite occurs with Brazil and Chile. This shows that Latin American countries do not have the same degree of integration, and it also shows that the speed of integration is quite different.
In the case of those markets that are less integrated (Argentina, Colombia and Peru), the D-CAPM plays a very important role because the proportion of statistically significant betas increases if only the downside systematic risk is considered: Argentina (87%), Colombia (74%) and Peru (76%). In the same way, the use of the D-CAPM in the other three markets increases the proportion of statistically significant betas, but on average these are of a lower magnitude than those obtained with the Global CAPM.
In general, the majority of the estimated costs equity is statistically significant; this is even true in the case of partially integrated markets where global betas were used to estimate Damodarans model and global and local betas to estimate the Lessards model, which are not reported. Furthermore, in the case of imperfectly diversified local institutional investors, the relative volatility ratio with Estradas model and with the Godfrey and Espinosas model, on average, is statistically significant at 95% confidence level in all countries.
Required return in Latin American emerging markets
This section shows the results of estimating equation (10a) using the cross-section time series method of Erb, Harvey and Viskanta (EHV). First, the equation (10b) was estimated using the semi-annual returns of the MSCI stock market indexes and the semi-annual country credit rating (CCR) for each country from September 1987 to March 2005. Then, the estimated parameters were used to fill equation (10a) to estimate the forward looking semi-annual required return per country using the last CCR corresponding to September 2005. This figure was finally annualized.
Table A13 shows the estimated required returns (RR) for seven Latin American emerging markets (including Venezuela). The first table shows the results considering all markets (emerging and developed); the second table shows the results considering only emerging markets and the third table shows the results considering developed markets and only Latin American emerging markets jointly.
As can be seen, the best results are obtained in the third estimation implying that Latin America as a region is different from the remaining emerging markets regions in the world; so, it only makes sense to compare it, as a region, with developed markets. However, the three results of Table A13 are consistent in the sense that they show that Chile has the lowest required return, while Argentina has the highest required return. Furthermore, the required returns obtained are higher than the costs of equity obtained before, which must be the case because we are dealing with credit risk as a total risk.
Even though these required returns are appropriate in the case of non-diversified entrepreneurs, there are two problems associated with these estimations: the CCR is updated only twice every year, and the required returns could only be estimated for the whole country. In fact, it is important to state that the goodness of fit of the regression between the stock exchange returns of the 46 countries considered (25 classified as emerging economies and 21 as developed countries) with the corresponding CCR is practically null (1%) (not reported). This implies that the variability of the returns is poorly accounted by the variability of the CCR due to its low frequency.
CONCLUSION
Given the previous results, it is important to point out that none of the previous methods account for all the features that one could face in emerging markets when trying to assess an investment project. These features are associated with the non-normality of stock and bond returns (negative skewness and excess of kurtosis), the lack of an enough time span for historical market data, the fact that markets are incomplete, the situation of partial integration and the heterogeneous degrees of diversification among investors in emerging economies.
Given the fact that stock returns are not allocated according to a normal distribution, it is not possible to use this argument to apply the CAPM as asset pricing model in emerging markets. The other possibility would be to assume a quadratic utility function, but it is well known in the literature that this specification is not adequate because it requires that the representative investors have a constant absolute risk aversion (CARA), which, in turn, implies that they will not change its optimal decision across time. This is clearly an unrealistic assumption.
Alternatively, the Arbitrage Pricing Theory (APT) or the three factor model of Fama and French (1993) may be used. However, there is no clear guidance concerning what are the right factors to apply in the case of the APT, and the investor is looking for long-term capital asset pricing model to valuate real investments. Therefore, the three factor model of Fama and French cannot be used because it is a short-term asset pricing model that takes into account anomalies that, in the long-term, should disappear.
Concerning the short time span for the historical market data, the situation is not possible to solve because, in order to estimate a decent market risk premium, it is necessary to have a long time span; otherwise, the standard error will be of such dimensions that it will leave a lot of uncertainty around the estimation. However, the latter problem is not the most important; the real concern is the negative market risk premiums obtained given the stock returns properties. In this case, a negative market risk premium does not have any financial meaning. Unfortunately, the local CAPM, the Lessards model, and the hybrid model rely upon local stock market data, that usually is not available or it is biased, due to the problems discussed above.
A market is called complete when it is simple to find a twin security that spans the risk of the non-traded asset for every possible state of nature and future period. In other words, when finding a quoted stock that can be used as a benchmark for the non-traded asset is relatively easy. Mongrut and Fuenzalida (2007) have shown that Latin American emerging markets are highly illiquid and that liquid stocks are concentrated around certain economic sectors. Hence, for the vast majority of economic sectors, it is not possible to find a twin security. Besides, as Bodnar et al. (2003) pointed out, the option of completing markets using market data from other stock markets is not a good choice given the restrictive assumptions that must be imposed and the poor estimations for emerging markets. Furthermore, it is important to state that the use of the CAPM is not justified in incomplete markets, even if twin assets could be found.
In particular, Herings and Kluber (2000) showed that the CAPM did not adjust to incomplete markets even with different probability functions for stock returns and different utility functions. However, given the low magnitude of the estimation errors obtained, these authors suggest that it is possible to apply it in incomplete markets, although it does not produce the desired results. Unfortunately, none of the previous models tackle really the problem of the emerging market incompleteness because this would imply to have many possible values for the investment project instead of just one market value. Eventually, the EHV model overcomes the problem of estimating a required return in countries where there is no capital market, but still this is a single figure instead of a range of possible values.
Most of the models deal with the situation of partial integration. Certainly it seems that the literature has been focused in this important fact and that the main variable to characterize this situation has been the country risk premium. All models of partial integration took into account the country risk either in the risk-free rate, the estimation of betas or in the market risk premium. From these three ways of including the adjustment for country risk, the D-CAPM and the Damodarans models are the only ones which are theoretically sound, given their assumptions, and realistic. The Hybrid and the Lessards models are also theoretically sound, but somehow misspecified because the partial integration is not necessarily linear and additive, and the systematic risk is not a crucial risk in emerging markets but total risk.
Hence, although the Damodarans and the Estradas models (D-CAPM) are the ones which are theoretically sound, they do not cope with all the necessary issues that must be taken into account when evaluating investment proposals in emerging markets. They do not deal with the problem of imperfect or non-diversification. It could be argued that this criticism is somehow unfair because these two models were put forward for well-diversified investors, but the fact that practitioners are using a version of these models to estimate the cost of equity for imperfectly diversified institutional investors produces a mental bias.
The Godfrey and Espinosa model lacks a theoretical foundation and certainly is an ad hoc specification based upon circumstantial empirical evidence. The Estrada (2000, 2001) specification is well-grounded in the capital market line (CML) when using the specification (9c). In fact, the underlying assumption is that the stock is perfectly correlated with the market index. However, this fails to recognize that many investment projects are actually not perfectly correlated with the market and an entrepreneur must pursue this goal. A better application of the Estrada proposal would be for estimating the required returns of venture capitalists that could have already a diversified investment portfolio that is not correlated to the market portfolio, and in RVR would be between the project and the venture capitalist investment portfolio instead of that of the market.
All the models, with the exception of the EHV model, seek to estimate the value of the project as if it were traded on the capital market; that is, they seek to estimate a market value for the investment project. However, in Latin American emerging markets there are numerous non-diversified entrepreneurs (more than 95% of the total number of companies) that are not corporate firms. In this sense, the valuation task in emerging markets goes far beyond finding a value for the investment project; it must aim to anticipate contingent strategies to face possible future scenarios. It must recognize that to find a unique estimation of the cost of equity would bias the investor mentality towards the illusion of one possible future instead of many possible ones.
In this sense, there are four main challenges that financial valuators must face in emerging markets:
1. To move from single point estimates of discount rates and project values to a range of possible values given the anticipated scenarios and contingent strategies that have been devised.
2. To develop theoretically sound models for estimating the cost of equity for imperfectly diversified institutional investors in emerging markets.
3. To develop theoretically sound models for non-diversified entrepreneurs in emerging markets.
4. To search for a better specification to characterize the situation of partial integration of emerging markets.
Besides, it should be noted that country risk affects in a different way each company. As Sabal (2004) has pointed out, in the case that the country risk is completely unsystematic, it would be incorrect to include it in the estimation of the discount rate. This is precisely the case of the non-diversified entrepreneurs that are fully exposed to country risk through the unanticipated variations in the local interest rates.
In this sense, it would more convenient to incorporate the country risk in the estimation of cash flows of the project through a prospective and risk analysis process instead of trying to summarize it into the discount rate. It should be considered that the underlying rationality of non-diversified entrepreneurs is quite different from the underlying rationality of global well-diversified investor17. Hence, valuators should stop using versions of the CAPM for well-diversified investors in the cases where non-diversified entrepreneurs want to assess their investment opportunities.
In the latter case, the discount rate will have necessarily a strong subjective component and the same will occur with the value of the project. This implies that the same project could have different values depending on the competitive advantages that entrepreneurs bring with them to the project. In this sense, the value obtained will no longer be a market value, but a required value given the project total risk that the entrepreneur is facing.
Paradoxically, proposals about how to estimate discount rates when subjectivity becomes relevant (i.e. non-diversified entrepreneurs) are scarce. This lack of proposals is really striking considering that these cases are the most important ones in Latin American emerging markets. Unless financial valuators address seriously the previous challenges, the practitioners will continue to valuate companies and investment projects as they valuate the 0.03% of traded companies in Latin America.
References
Adler, M., & Dumas, B. (1983). International Portfolio Choice and Corporation Finance: A Synthesis. The Journal of Finance, 38, 925-984. [ Links ]
Bodnar, G., Dumas, B., & Marston, R. (2003). Cross-Border Valuation: The International Cost of Equity Capital (NBER Working Paper Series, No 10115). Cambridge, MA: NBER. [ Links ]
Collins, D., & Abrahamsom, M. (2006). Measuring the Cost of Equity in African Financial Markets. Emerging Markets Review, 7, 67-81. [ Links ]
Damodaran, A. (2002a). Estimating Equity Risk Premiums (Working paper). New York: NY University, Stern School of Business. [ Links ]
Damodaran, A. (2002b). Investment Valuation: Tools and Techniques for Determining the Value of any Asset. (2nd. Ed.). New York: Wiley Frontiers in Finance. [ Links ]
Damodaran, A. (2003). Measuring Company Exposure to Country Risk: Theory and Practice (Working paper). New York: NY University, Stern School of Business. [ Links ]
Dimson, E., Marsh, P., & Staunton, M. (2003). Global Evidence on the Equity Risk Premium. Journal of Applied Corporate Finance, 15(4), 27-38. [ Links ]
Erb, C., Harvey, C., & Viskanta, T. (1995). Country Risk and Global Equity Selection. The Journal of Portfolio Management, 21(2), 74-83. [ Links ]
Erb, C., Harvey, C., & Viskanta, T. (1996a). Political Risk, Financial Risk and Economic Risk. Financial Analysts Journal, 52, 28-46. [ Links ]
Erb, C., Harvey, C., & Viskanta, T. (1996b). Expected Returns and Volatility in 135 Countries. The Journal of Portfolio Management, 22(3), 46-58. [ Links ]
Estrada, J. (2000). The Cost of Equity in Emerging Markets: A Downside Risk Approach. Emerging Markets Quarterly, (Fall), 19-30. [ Links ]
Estrada, J. (2001). The Cost of Equity in Emerging Markets: A Downside Risk Approach (II). Emerging Markets Quarterly, (Spring), 63-72. [ Links ]
Estrada, J. (2002). Systematic Risk in Emerging Markets: The D-CAPM. Emerging Markets Review, 3(4), 365-379. [ Links ]
Estrada, J., & Serra, A. (2005). Risk and Return in Emerging Markets: Family Matters . Journal of Multinational Financial Management, 15(3), 257-272 [ Links ]
Fama, E., & French, K. (1993). Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics, 33, 3-56. [ Links ]
Fama, E., & French, K. (1997). Industry Cost of Equity. Journal of Financial Economics, 43, 153-193. [ Links ]
Ferson, W., & Locke, D. (1998). Estimating the Cost of Capital through Time: An Analysis of the Sources of Error. Management Science, 44(4), 485-500. [ Links ]
Fornero, R. (2002). Valuación de empresas en mercados financieros emergentes: riesgo del negocio y tasa de actualización (Working Paper). Mendoza, Argentina: Universidad Nacional de Cuyo. [ Links ]
Fuenzalida, D., Mongrut, S., & Nash, M. (2005). Riesgo país y riesgo soberano: Concepto y medición. Revista Mexicana de Economía y Finanzas, 4(4), 347-367. [ Links ]
Godfrey, S., & Espinosa, R. (1996). A Practical Approach to Calculating Costs of Equity for Investments in Emerging Markets. Journal of Applied Corporate Finance, 9(3), 80-89. [ Links ]
Harvey, C. (2000). The Drivers of Expected Returns in International Markets. Emerging Markets Quarterly, (Fall), 1-17 [ Links ]
Harvey, C. (2001). The International Cost of Capital and Risk Calculator (Working Paper). Durham, PA: Duke University. [ Links ]
Harvey, C. (2004). Country Risk Components, the Cost of Capital and Returns in Emerging Markets (ICCRC Working Paper). Durham, PA: Duke University. [ Links ]
Herings, J., & Kluber, F. (2000). The Robustness of CAPM- A Computational Approach. (Research Memoranda, No 035). Maastricht, The Netherlands: METEOR, Maastricht University. [ Links ]
International Finance Corporation. (1999). Emerging Stock Markets Factbook 1999. Washington D. C.: Author. [ Links ]
Koedijk, K., & Van Dijk, M. (2004). Global Risk Factors and the Cost of Capital. Financial Analysts Journal, 60(2), 32-38. [ Links ]
Koedijk, K., Kool, C., Schotman, P., & Van Dijk, M. (2002). The Cost of Capital in International Financial Markets: Local or Global?. Journal of International Money and Finance, 21(6), 905-929. [ Links ]
Lessard, D. (1996). Incorporating country risk in the valuation of offshore projects. Journal of Applied Corporate Finance, 9(3), 52-63. [ Links ]
Lintner, J. (1965). The Valuation of Risky Assets and the Selection of Risky Investment in Stock Portfolios and Capital Budgets. Review of Economics and Statistics, 47, 13-37. [ Links ]
Mariscal, J., & Lee, R. (1993). The Valuation of Mexican Stocks: An Extension of the Capital Asset Pricing Model. New York: Goldman Sachs. [ Links ]
Markowitz, H. (1959). Portfolio Selection. London. Yale University Press. [ Links ]
McMahon, R., & Stanger, A. (1995). Understanding the Small Enterprise Financial Objective Function. Entrepreneurship Theory and Practice, 19(4), 21-40. [ Links ]
Mishra, D., & O Brien, T. (2005). Risk and Ex Ante Cost of Equity Estimates of Emerging Market Firms. Emerging Markets Review, 6(2), 107-120. [ Links ]
Mongrut, S., Palacios, L, Rosales, L., & Fuenzalida, D. (2010). Performance of Peruvian Pension Funds: Do Limits for Foreign Investments Matter? (Working Paper). Mexico: ITESM. [ Links ]
Mongrut, S. (2007). Valuation of Investment Projects in Latin American Emerging Economies: The Case of Non-diversified Entrepreneurs. Unpublished Ph. D. thesis, University of Barcelona, Spain. [ Links ]
Mongrut, S., & Fuenzalida, D. (2007). Valoración de inversiones reales en Latinoamérica: hechos y desafíos. Académicos, 2(4), 67-80. [ Links ]
Mongrut, S., & Ramírez, D. (2006). Discount Rates in Emerging Capital Markets. ICFAI Journal of Financial Economics, 4(2), 35-55. [ Links ]
Mossin, J. (1966). Equilibrium in a Capital Asset Market. Econometrica, 34(4), 768-783. [ Links ]
Pereiro, L., & Galli, M. (2000). La determinación del costo de capital en la evaluación de empresas de capital cerrado: una guía práctica. (Monografía). Buenos Aires, Argentina: Instituto Argentino de Ejecutivos de Finanzas. [ Links ]
Pereiro L. (2001) The Valuation of Closely-Held Companies in Latin America. Emerging Markets Review, 2(4), 330-370. [ Links ]
Sabal, J. (2004). The Discount Rate in Emerging Markets: A Guide, Journal of Applied Corporate Finance, 16(2-3), 155-166. [ Links ]
Sharpe, W. (1964). Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. Journal of Finance, 19, 425-442. [ Links ]
Siegel, J. (2002). Stocks for the Long Run: The Definitive Guide to Financial Market Returns and Long-Term Investment Strategies. (3rd Ed.). New York: McGraw Hill. [ Links ]
Solnik, B. (1974). An Equilibrium Model of the International Capital Market. Journal of Economic Theory, 8, 500-524. [ Links ]
Stevenson, S. (2001). Emerging Markets, Downside Risk and the Asset Allocation Decision. Emerging Markets Review, 2(1), 50-66. [ Links ]
Stulz, R. (1995). Globalization of Capital Markets and the Cost of Capital: The Case of Nestlé. Journal of Applied Corporate Finance, 8(3), 30-38. [ Links ]
Walker, E. (2003) Costo de capital para empresas reguladas en Chile. Informe para el Ministerio de Economía, Fomento y Turismo del Gobierno de Chile. Santiago de Chile: Pontificia Universidad Católica de Chile. [ Links ]
NOTAS DE PIE
* The authors are grateful to the National Fund for Scientific and Technological Research (FONDECYT) and the National Research and Technological Committee (CONICYT) from Chile for funding this research (project No 1090440). We are also grateful to the participants at the VIIth International Conference of Finance in Monterrey, Mexico, for their valuable comments. Correspondence with authors: Samuel Mongrut, EGADE Zona Centro, Tecnológico de Monterrey, Epigmenio Gonzalez No 500, Fracc. San Pablo, C.P. 76120, Querétaro, México.
1 To obtain a fair value, the equilibrium model is generally used.
2 In several Latin American countries pension funds are legally limited to invest abroad. For example, the investment limit for foreign investments of Peruvian Pension Funds is 12.5% (Mongrut, Palacios, Rosales, & Fuenzalida, 2010).
3 In the year 2000, the IFC sold the rights of this database to Standard & Poors.
4 MSCI stands for Morgan Stanley Capital International, a large provider of data.
5 Fuenzalida, Mongrut and Nash (2005) discuss alternative ways to estimate the sovereign risk.
6 The separation property states that a combination of a risk-free portfolio with an efficient risky portfolio yields another efficient portfolio.
7 Bodnar, Dumas and Marston (2003) use a similar argument to arrive to the same conclusion.
8 Estrada proposed these measures for stock exchange indexes in his work of year 2000, and for industries in his paper of year 2001. Nevertheless, his argument can be extended to individual securities.
9 The implicit cost of capital is the discount rate that makes the present value of the expected cash flows of a company (based on the projections from analysts) equal to the current market value of the company (Harvey, 2004).
10 Upon estimating the alpha parameters in equation (10b) the last observation corresponding to the CCR must be left aside so that this value may be replaced in equation (10a).
11 The number of securities considered by economic sector and per country is available upon request.
12 Note that currently the estimated US annual market risk premium is around 3% using more than 200 years of data (Dimson, Marsh, & Staunton, 2003; and Siegel, 2002). This would be the most adequate US market risk premium to use instead of the 5.5% that it is used here for comparison purposes.
13 The estimated costs of equity using each one of these models are not reported in this work, but are available on request.
14 An alternative methodology is the one followed by Collins and Abrahamson (2006). These authors obtained a market index per sector and per country and then they estimated the cost of equity of each economic sector. This methodology is not adequate for Latin American capital markets because they are heterogeneous with respect to the number of liquid securities per sector.
15 The Three Factor Model is a multifactor model assumes that additionally to the market risk premium there are two other factors that help to explain the cross-sectional variation of stock returns: the book-to-market ratio and size. These latter two factors are being considered anomalies and are supposed to disappear in the long-term; this is the reason why one does not consider this model in this research.
16 All periods begin in January of the corresponding year and end in December of the fifth consecutive year, with the exception of the last estimation period that begins in January of the year 2000 and ends on October 31st, 2005.
17 McMahon and Stanger (1995) analyze the underlying rationality of small entrepreneurs, which turns out to be complicated.
Anexos
Consultar anexos completos en pdf