Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Journal of Economics, Finance and Administrative Science
versão impressa ISSN 2077-1886
Journal of Economics, Finance and Administrative Science v.16 n.31 Lima dez. 2011
ARTICLES
Análisis de comportamiento caótico en variables de la cadena de suministro
Analysis of chaotic behaviour in supply chain Variables
Sergio A. Ramírez1
; Gloria E. Peña21 Magíster en Sistemas. Universidad EAFIT – Bogotá, Colombia. <ramire@eafit.edu.co>
2 Doctora en Ingeniería de Organización. Universidad Nacional de Colombia, Escuela de Ingeniería de la Organización, Medellín. <gepena@unal.edu.co>.
Resumen
Este artículo desarrolla un modelo de cadena de suministro de cuatro niveles mediante la utilización de la dinámica de sistemas con el software Ithink® y Mathlab® para el análisis de los datos. La cadena de suministro se estudia a partir de la Teoría del Caos, teoría que ayuda a identificar cuáles son las variables más sensibles que puedan llevar a un estado de caos.
Se construye un modelo de estructura genérica que comprende los eslabones de fábrica, distribución, mayorista, minorista y cliente. Se simula la dificultad que los gerentes de operaciones y logística encuentran para decidir sobre cuánto ordenar y en qué momento, de acuerdo con lo que ocurre en los eslabones del nivel anterior y posterior, mediante dos parámetros de decisión: el primer parámetro denominado A indica la participación de la cantidad de unidades (entre 0 y 1) que se tiene en cuenta de los productos en el inventario actual y los pedidos pendientes, al momento de hacer el pedido. El segundo parámetro denominado B es la participación de la cantidad de unidades (entre 0 y 1) que se encuentran en la línea de suministro (en tránsito) al momento de hacer el pedido en cada uno de los eslabones de la cadena de suministros.
Palabras claves: Administración de la cadena de suministros, logística, Teoría del Caos, dinámica de sistemas, simulación, Juego de la Cerveza.
Abstract
In this article we develop a supply chain model of four levels through the utilization of system dynamics with Ithink® and Mathlab® softwares to analyze data. The supply chain is studied from the chaos theory perspective, which helps identifying the sensitive variables that can lead to a state of chaos. A generic structure model that comprehends factory links, distribution, wholesale, retail and the client is constructed. The difficulty of operations and logistics managers to decide how much to order and when to do it is simulated accordingly to what occurs in the links of the preceding and subsequent levels with two decision parameters: The first parameter denominated A indicates the participation (between 0 and 1) of the number of product units that are taken into account in the actual stock and the pending orders at the moment of performing an order. The second parameter, denominated B, is the participation (between 0 and 1) of the number of units in the supply line (in transit) at the moment of performing orders of each of the links of the supply chain.
Keywords: Supply chain management, logistics, Chaos Theory, system dynamics, simulation, Beer Game.
INTRODUCCIÓN
Las empresas de clase mundial fijan objetivos a corto, mediano y largo plazo, con el fin de adaptarse a los continuos cambios que el mercado exige. La administración de operaciones y la cadena de suministro tienen hoy gran importancia dentro de estas empresas en el sentido que se ha convertido en parte fundamental dentro del proceso de alcanzar los objetivos estratégicos. Las operaciones internas y externas que las empresas requieren para cumplir sus metas deben ser minuciosamente analizadas para que se cumplan de manera eficiente y rápida los compromisos adquiridos al exterior (con clientes, proveedores, etc.) y al interior de la empresa.
Este artículo plantea los efectos de la toma de decisiones a partir la Dinámica de Sistemas y del Pensamiento Sistémico, como una forma de conectar procesos y ejecuciones entre sí, y relacionarlos de tal manera que se entienda que cada proceso-acción-ejecución afecta al siguiente o al anterior (Sterman, 2000). Si se visualiza la cadena de suministro de una empresa y todos sus procesos internos y externos como una estructura en que el caos y lo impredecible pueden afectar las variables claves, es posible reaccionar de una manera más eficiente a los retos que esta complejidad genera, recomendar qué variables estimular e identificar tendencias y comportamientos (Mosekilde & Larsen, 1988).
Dentro de la cadena de suministro existen eslabones o niveles que interactúan y se afectan mutuamente, entre los que tenemos, por ejemplo: abastecimiento de materias primas, los procesos productivos, el almacenamiento, la distribución, comercialización y el cliente final (Chopra & Meindil, 2008). Aquí se muestra de manera sistémica la fábrica, el distribuidor, el mayorista y el minorista para el proceso de simulación. Al finalizar esta simulación, se identificarán las variables que integran la cadena de suministro que tienden a generar caos. De esta manera se identificará y recomendará cuáles podrían ser los fenómenos más importantes a evitarse y de esta forma evadir el caos y trabajar en toda la cadena de una manera más eficiente y ordenada.
El modelo muestra una gran variedad de comportamientos dinámicos incluyendo oscilaciones de ciclos limitados de diferente periodicidad y caos determinístico. En el marco analítico del trabajo también se aporta la bibliografía y las investigaciones que se han dado sobre el tema. Si bien la teoría del caos ha sido motivo de estudio a lo largo de la historia, su aplicación a la dinámica de sistemas y la cadena de suministro ha sido poco reseñada. Con las conclusiones y recomendaciones finales se pretende ampliar lo estudiado hasta ahora y suministrar a los gerentes de operaciones y logísticos información clave para reaccionar mejor ante los retos que implica el caos.
MARCO TEÓRICO
Durante los años 50 del siglo pasado se desarrolló la dinámica de sistemas y se han construido muchos modelos, siguiendo los principios de esta disciplina, en áreas tan diversas como las ciencias sociales, económicas, ambientales, administrativas y biológicas. A continuación, se hace una reseña de las investigaciones que han contribuido al desarrollo de las operaciones, la administración de la Cadena de suministros o Supply Chain Management, (SCM por sus siglas en inglés) y el caos.
Con la aparición de los computadores digitales y la dinámica de sistemas, el profesor Jay W. Forrester del Massachusetts Institute of Technology (MIT) publicó en 1961 el libro Industrial Dynamics. Esa misma obra se publica una versión revisada en el año 1971. Forrester es el primero en formalizar la dinámica de sistemas en problemas de la administración de la cadena de abastecimiento. En esta obra fundacional, Forrester describe un modelo de un sistema de producción – distribución en términos de seis flujos que interaccionan entre sí: información, materiales, órdenes, dinero, fuerza laboral y equipos. El modelo se construye mediante una fábrica, una bodega, un distribuidor y un minorista. Basado en este modelo, Forrester investiga los temas relacionados con la cadena de abastecimientos como, por ejemplo, las oscilaciones en los inventarios de los diferentes actores cuando ocurren cambios en la demanda del cliente y muestra la amplificación del fenómeno, desde el minorista hasta la fábrica, así como cuál es el impacto de las tecnologías de información en los procesos administrativos. Especialmente se centra en el carácter de la realimentación de la información (feedback) en el sistema industrial y usa un modelo para el planeamiento de la organización en una forma perfeccionada. También se refiere a las oscilaciones de las variables utilizadas, a través del tiempo, para analizar la estructura de la organización, la amplificación de las órdenes y las demoras (de decisiones y acciones). Forrester los toma en cuenta con el fin de mejorar tanto la toma de decisiones relacionada con los aspectos estratégicos y tácticos como para ayudar en la ejecución automática de un juicio de valor (1971).
El estudiante debe reconocer, localizar, y diagnosticar comportamientos caóticos; la pregunta del profesor es cómo se debe abordar la tarea pedagógica ante estos retos. Andersen y Sturis (1988) han propuesto que la manera más económica para enseñar principios generales en sistemas dinámicos es organizar un número pequeño de ejemplos cuidadosamente elegidos. A través de estos ejemplos se podrían ver las relaciones entre la estructura y comportamiento del sistema. Los autores también han propuesto la noción de estructuras por catálogos como una forma de organización de las clases introductorias a sistemas dinámicos.
Para demostrar el impacto en la cadena de abastecimientos, en 1989 Sterman condujo un experimento para simular el manejo de la producción y distribución industrial: el "Juego de la Cerveza". En este ahora clásico caso se incluyen varios actores, realimentaciones y retardos a lo largo de la línea de abastecimiento. En el juego se observa cómo el sistema exhibe tres comportamientos: oscilación, amplificación de las órdenes y retrasos en la cadena. Todo esto se debe a la poca percepción de realimentación; sin embargo, en la vida real es importante que los gerentes tengan acceso a más información de la que se dispone en el experimento. En el juego de la cerveza, las oscilaciones se deben a que las reglas de decisión no tienen en cuenta los retrasos de materiales e información que hay entre el momento en que se pone la orden y el momento en que se reciben los materiales; al mismo tiempo, se explica el razonamiento utilizado por las personas para la toma de decisiones (Sterman, 1989).
En el año 2005, la revista Systems Dynamics Review (2005) publicó una edición especial dedicada a las cadenas de suministros y redes de abastecimiento. En la publicación aparecen varios artículos, que a continuación se reseñan. Akkermans y Dellaert, por ejemplo, realizan un estudio sobre las contribuciones de la dinámica de sistemas al SCM hasta el 2005. Encuentran que las suposiciones más comunes en las investigaciones de modelación de cadenas de abastecimiento incluyen la acumulación de la demanda, funciones de costos lineales, capacidad infinita, los lead times constantes y demanda constante. Por otro lado, los autores llegaron a la conclusión de que por lo general la meta común de estas investigaciones es la minimización de los costos manteniendo el inventario con la condición de conseguir un cierto nivel de servicio para el cliente, o reducir las variaciones (oscilaciones) del inventario (Akkermans & Dellaert, 2005).
Por su parte, Goncalves, Hines y Sterman estudian el impacto de la demanda endógena en los sistemas de producción híbridos push-pull, para lo cual construyen un modelo de la cadena de abastecimientos de los semiconductores de Intel. Los autores analizan cómo responde la empresa a la demanda de los clientes con niveles de servicio variables teniendo en cuenta dos efectos: (1) el efecto de las ventas y (2) el efecto de la producción. En una realimentación negativa, el primero señala cómo la escasez de producto influye en los clientes que buscan otras fuentes de abastecimiento en la competencia, lo que redujo la demanda y disminuyó la escasez en Intel. El segundo efecto captura el impacto de los cambios en la demanda y, por ende, en las decisiones de producción del fabricante: menos demanda lleva a una reducción de la producción (de la utilización de la capacidad) para evitar tener excesos de inventario. Al bajar la producción se tendrán bajos inventarios y bajos niveles de servicio al cliente por escasez de producto. Esto deprime aún más la demanda en un ciclo de retroalimentación positiva. Es decir, que el efecto de la producción genera una reacción que ahonda la perturbación original. También muestra cómo el sistema híbrido se puede convertir en un sistema push, si se agotan los inventarios de productos terminados. (Goncalves, Hines, & Sterman, 2005).
Anderson Jr., Douglas y Lundeen estudian el manejo de la capacidad en cadenas de abastecimiento de empresas de servicio y de manufactura hechos a la medida. En este tipo de cadenas no existen inventarios de producto terminado, sino que los trabajos atrasados se van acumulando y únicamente se pueden manejar ajustando la capacidad. Para tratar este problema, los autores desarrollaron un modelo en dinámica de sistemas, en el que se determina que la reducción del lead time en las empresas de servicio puede reducir los trabajos acumulados a corto plazo si no se coordina con un ajuste de la capacidad, aunque se incrementen a largo plazo. (Anderson Jr., Morrice, & Lundeen, 2005).
Un componente importante en la efectividad de la administración de la cadena de abastecimiento, especialmente en las compañías basadas en sistemas push, es la planeación de la demanda. Una evaluación precisa de la demanda del cliente impacta en aspectos como los niveles de inventario, en el comportamiento de los proveedores y en el transporte. La demanda de los clientes genera gran impacto y complejidad en la administración de la cadena de abastecimiento, y algunos autores explican su comportamiento en la aleatoriedad. La teoría de caos puede ayudar a explicar el aparente comportamiento aleatorio y desordenado de la forma de pedir de los clientes (Drew, Joe, & Jonatha, 2006).
En la cadena de abastecimiento se presenta el efecto látigo, efecto que se investigó en el artículo de Seung-Kuk Paik, y Prabir K Bagchi (2007). En el artículo, los autores determinaron las contribuciones más representativas de cada una de las causas del efecto látigo, identificaron cuáles de éstas causas tienen un impacto significativo en la cadena de abastecimiento y los aspectos considerados más relevantes. Las posibles causas que dan origen al efecto látigo presentes en los modelos de simulación son nueve; de las cuales seis factores son estadísticamente significativos: (1) actualización del pronóstico de la demanda; (2) ordenamiento por lotes; (3) demoras del material; (4) demoras de información; (5) demoras de compras y, (6) nivel de escalones o eslabones. De estos seis factores, los más significativos son la actualización del pronóstico de la demanda, el nivel de escalones o eslabones y las demoras de compras (la variación de los precios) (Paik & Bagchi, 2007).
Estos comportamientos dinámicos y complejos mencionados pueden ser correctamente modelados adoptando un acercamiento a la dinámica de sistemas, particularmente bajo una perspectiva de caos. La Teoría del Caos es una evolución desordenada de largo término que ocurre en un sistema no lineal determinístico. Dicha teoría tiene relación con el comportamiento caótico (caos) en sistemas dinámicos no lineales. Según Hwarng & Xie (2008), un sistema bajo caos se caracteriza por lo siguiente
-
Aleatoriedad y no linealidad.
-
Desorden aparente: las variables se ven desordenadas e irregulares.
-
Atractores extraños: orden, estructuras o caminos que pueden ser encontrados en un espacio de fase.
-
Sobresaltos: los rangos de las variables tienen saltos finitos.
-
Sensibilidad a las condiciones iniciales del sistema: un cambio pequeño en las condiciones iniciales puede tener grandes efectos en la evolución del sistema.
MODELO DE CADENA DE SUMINISTROS PARA EL ESTUDIO DE CAOS
El modelo construido en el presente artículo utiliza la dinámica de sistemas y el muy popular "Juego de la Cerveza", sobre administración, operaciones y logística creado por un grupo de profesores de la MIT Sloan School of Management, Massachusetts. El juego consiste en una cadena de suministro (sistema) de cuatro niveles que incluye la fábrica, el distribuidor, el mayorista y el minorista que atiende la demanda externa.
El modelo se evalúa mediante diversas pruebas, y sus parámetros de decisión varían siguiendo el comportamiento de la cadena de suministro en el modelo de producción y distribución, similar al del juego de la cerveza realizado por Jarmain y Sterman (Larsen, Morecroft, & Thomsen, 1999). Además, se modifican las condiciones iniciales de la estructura, para así encontrar las variables que afectan la política de órdenes y de inventarios durante el estado de caos.
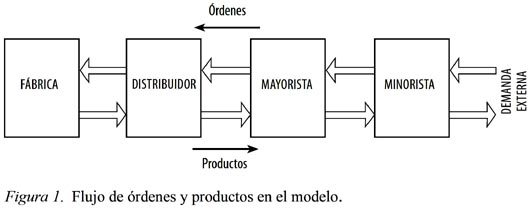
En el modelo propuesto, las órdenes circulan hacia la izquierda y el producto fluye hacia la derecha, como se muestra en la Figura 1 dependiendo de los requerimientos de los clientes finales, representados por la demanda.
En la Figura 2, la parte superior del modelo en línea de suministro del mismo. Finalmente, las ventas Ithink® se identifica como la zona de decisión, donde también se ven afectadas por la cantidad de inventario los agentes o individuos de cada nivel ejecutan el sistema mediante lo que piensan ordenar. Ellos deciden cuánto del inventario actual, o de lo que viene en camino, se utilizará de acuerdo con los parámetros A y B que se definieron en el resumen.
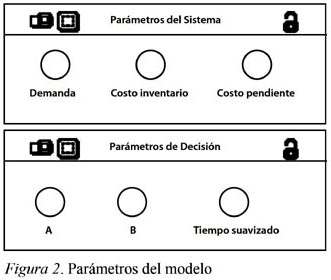
A continuación se explican las variables, los flujos y las conexiones del modelo. Los parámetros del modelo son representados mediante variables auxiliares tomando datos de entrada que sirven para realizan cálculos y se convierten en datos de salida como se muestran en la Figura 2. La demanda se conecta al flujo de venta del minorista y al flujo de pendientes del mismo. Luego, se crea un flujo de inventario que entra al minorista que va a afectar las ventas y al flujo de la línea de suministro del mismo. Finalmente, las ventas
también se ven afectadas por la cantidad de inventario en un momento t del minorista (ver Figura 3).
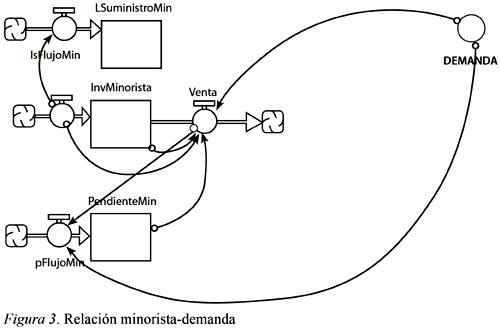
La red del minorista con la demanda externa se conecta al flujo de entrada del minorista con las ventas del mayorista; este es el inventario que llega al minorista para disponer de él con el fin de suplir la demanda (ver Figura 4).
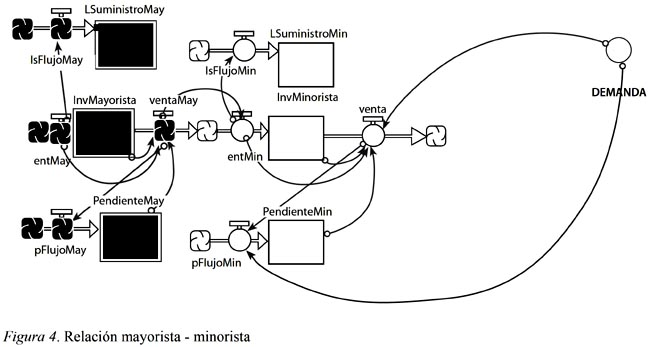
El flujo de entrada del mayorista es afectado por las ventas del distribuidor y el inventario de este es afectado por un nuevo flujo; esta vez es el flujo de ventas de la fábrica (ver Figura 5). La red del distribuidor se construye de la misma forma que las redes del minorista y del mayorista, con sus respectivos flujos de línea de suministro y de órdenes pendientes por despachar.
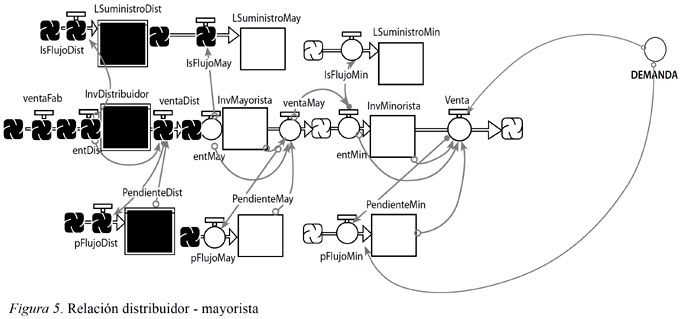
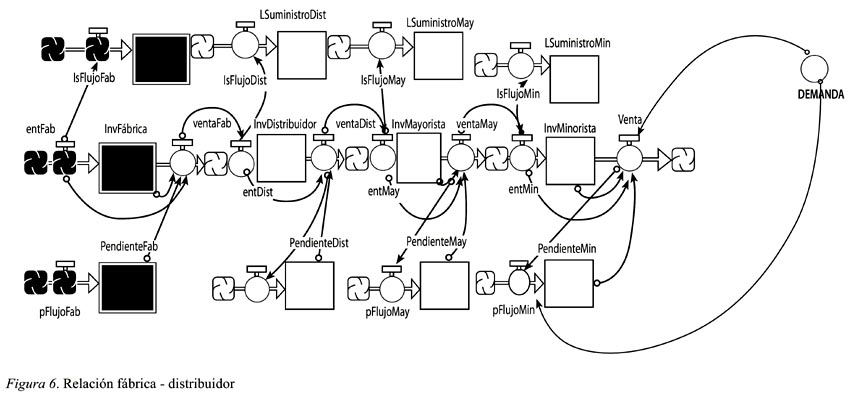
De la misma manera, las redes ya construidas de minorista, mayorista y distribuidor se adicionan a la red principal, que es la red de la fábrica, con sus flujos de línea de suministro, inventario y órdenes pendientes (ver Figura 6).
Los efectos de los parámetros de decisión A, B y el tiempo de suavizado (TiempoSuavizado) se agregan a las redes que, a su vez, afectan la cantidad a ordenar en cada nivel, en este caso, el pedido del minorista (ver Figura 7). El tiempo suavizado es un parámetro que indica durante cuánto tiempo se toma de la demanda actual y se da un peso para suavizarla. En el caso de nuestro modelo se utiliza una demanda semanal, por lo que se suaviza la función de demanda en el período de la modelación.
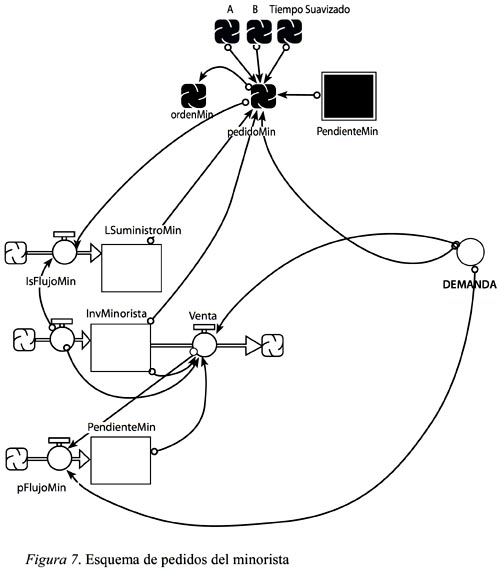
El pedido del minorista afecta el flujo de la línea de suministro en el momento en que la orden se genera (ordenMin).Asimismo, se ven afectados por la demanda, la línea de suministro, el inventario del minorista y las órdenes pendientes del mismo. El sistema se comporta de la misma forma en cada nivel (fábrica, distribuidor y mayorista). En otra palabras, las órdenes generadas afectan el eslabón anterior.
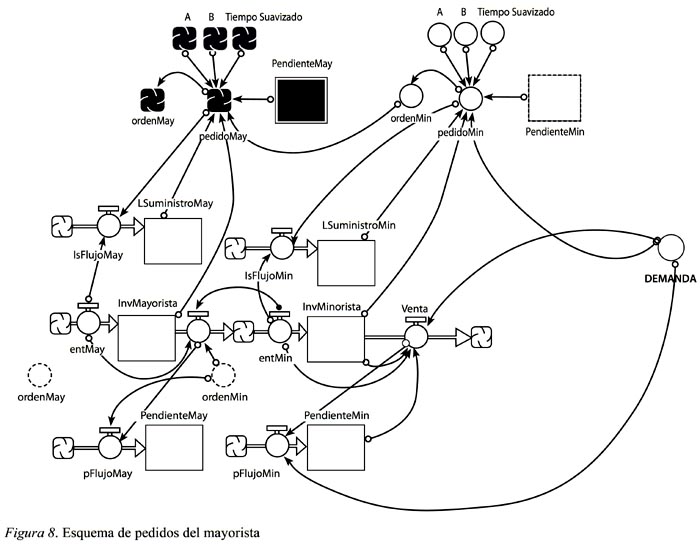
La orden del minorista influenciará la forma en que el mayorista hará su pedido; este, a su vez, afectará la red del mayorista (como se ve en la Figura 8), y la orden del minorista influirá en el flujo entrante del distribuidor. La orden del minorista estimula las ventas del mayorista y su flujo de órdenes pendientes.
A la red del distribuidor también se le agrega su respectiva red de decisión, afectada por los parámetros A, B y el Tiempo de suavizado. La orden generada por el distribuidor afecta el flujo de inventario que llega de la fábrica (ver Figura 9).
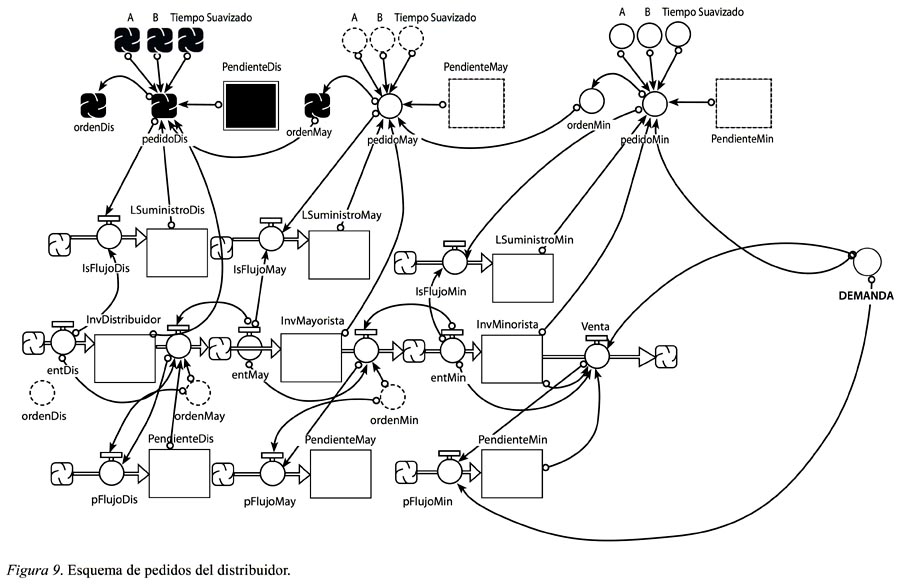
Finalmente la fábrica también se rige por los parámetros de decisión, y su pedido generará una orden de fabricación. Esta estará representada por la variable entrante que alimenta el flujo de producción que suple el inventario de la fábrica (ver Figura 10).
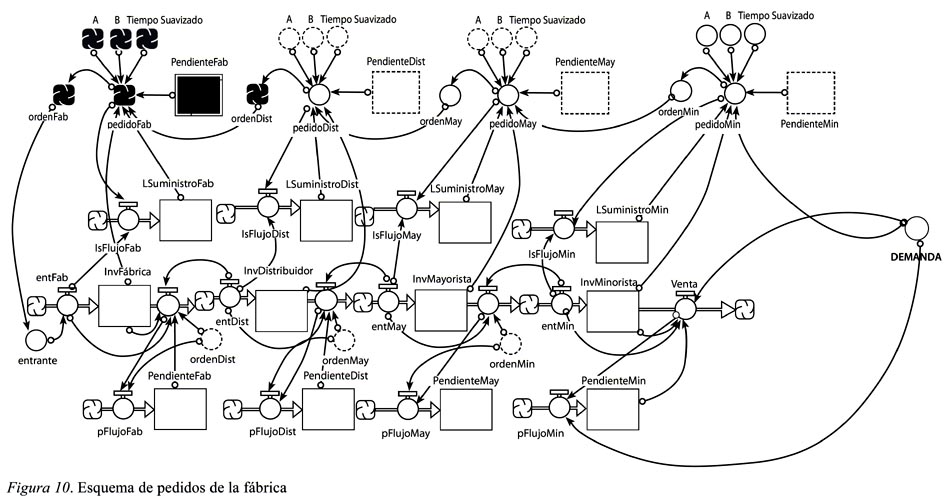
En la Figura 11 se observa el modelo completo con las zonas de decisión y del sistema que se delimitan para una fácil identificación.
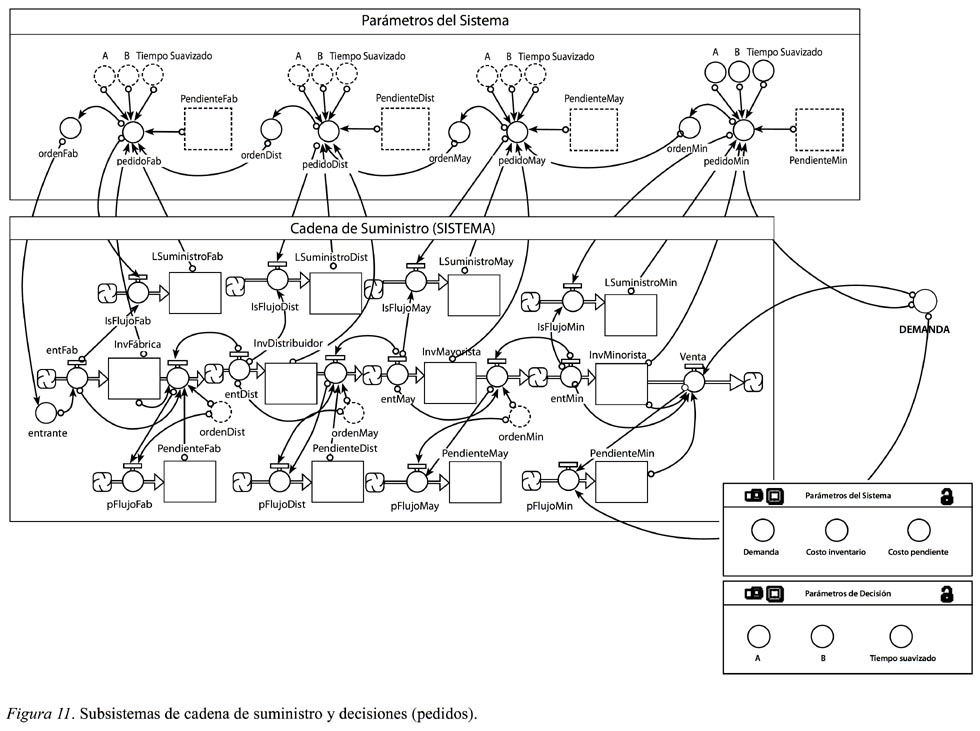
Es posible calcular la cantidad de inventario efectivo en cada nivel con las variables del inventario y de las órdenes pendientes. El inventario efectivo es de gran ayuda para la interpretación gráfica del efecto de los parámetros A y B en el sistema. En la red se calcula el costo total de mantener el inventario y el de venta perdida (no se tiene inventario disponible para satisfacer la demanda), representado por las variables de inventario y órdenes pendientes de cada nivel, como se ven en la Figura 12.
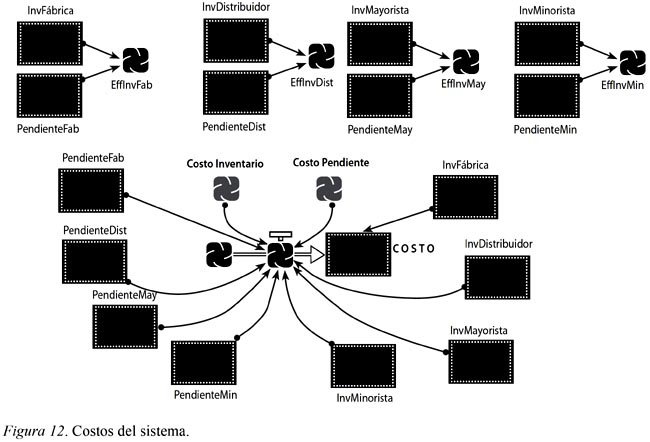
El modelo completo, como muestra la Figura 13, consta entonces de las tres zonas: parámetros, decisión y cadena de suministro, así como dos redes de inventario efectivo y costo total.
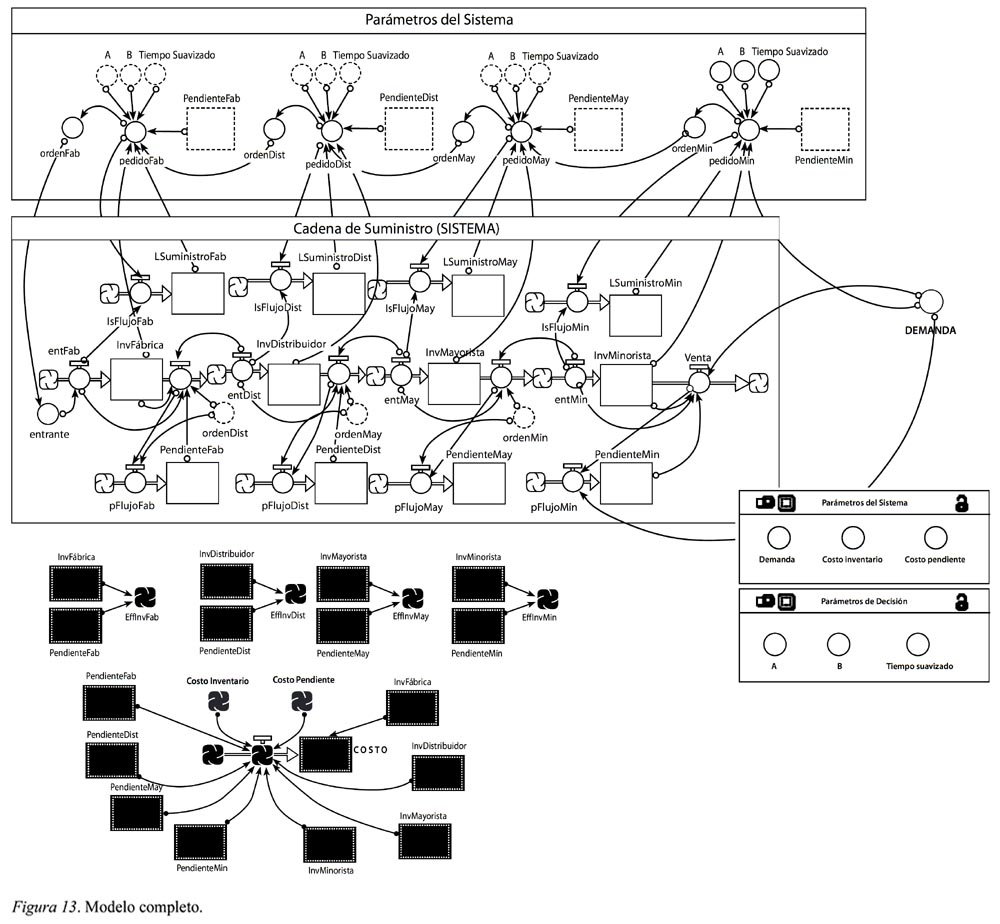
ANÁLISIS DE RESULTADOS
Después de construido el modelo, y con las ecuaciones ingresadas, se simula el funcionamiento de la cadena bajo unas condiciones iniciales variando los parámetros A y B explicados a continuación. Para escoger los parámetros se debe tener en cuenta que las decisiones de pedidos tomadas por los agentes de cada nivel de la cadena sean las variables que más influyen en el sistema. Los parámetros A y B son valores que representan al valor heurístico utilizado por algunos de los agentes (gerentes) que hacen los pedidos en cada nivel. Los criterios A y B significan la cantidad unidades que se tiene en cuenta en las decisiones. La variación de los parámetros se realiza de la siguiente manera:
A se varía con un ∆A de 0.01, tomando valores desde 0 hasta 1. Así se tiene valores para A de 0, 0.01, 0.02, , 0.99, 1.
Al mismo tiempo, se varía B con un ∆B de 0.01 en la región de 0 a 0.3 y con un ∆Bde 0.05en la región de 0.3 a 1. El cambio más pequeño en la región de 0 a 0.3 es porque los mayores cambios de los valores de las variables se presentaron para esos valores de B, debido a que se desea recoger un mayor nivel de detalle en el comportamiento de la variable.
Con las variaciones de A y de B se obtienen 4545 datos (101 en A y 45 en B) para las diferentes opciones (101 *45 = 4545) de las dos variable evaluadas. Dichos datos se tomaron de Ithink® con la ayuda de la opción de "Análisis de Sensibilidad" (SensiSpecs) que incluye la herramienta.
En sensi-specs se puede variar automáticamente un parámetro a la vez. En este caso, el parámetro escogido es A; es decir, dado un valor del parámetro B (introducido manualmente), se obtienen 101 resultados de la simulación mediante la opción de Variation Type: Incremental.
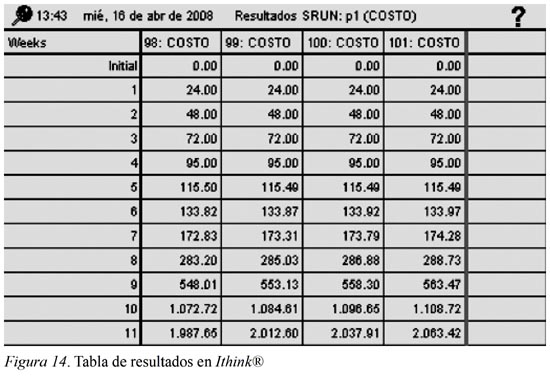
Se introduce un parámetro B cualquiera (por ejemplo B=0.01) y se corre el modelo con la opción S-RUN (Simulación teniendo en cuenta los parámetros de sensibilidad). Esta simulación guarda los datos de 101 corridas en una tabla de resultados. Los datos de cada corrida incluyen los valores en cada instante de tiempo (0 a 49 semanas) para las 5 variables escogidas para así obtener los resultados y realizar el análisis de caos: costo, PedidoMay, EffInvMay, InvMinorista, LSuministroDist. Al escoger el parámetro B=0.01 se tienen las variaciones de A=0,0.01, ,0.99, 1, por lo que para cada variable se obtendrían 101 variaciones de A por 50 semanas (desde la 0 a la 49), dando un total de 5050 datos por valor de B por variable. Así, con 45 valores de B (0, 0.01, , 0.29, 0.3, 0.35, , 0.95, 1) y 5 variables se obtiene un total de 1136.250 datos que se deben manejar.
La tabla con los resultados se llama "Resultados SRUN". En cada página de dicha tabla se guarda una variable para así comparar los resultados de las 101 corridas. De esta manera se puede escoger la opción Comparative que se encuentra en las opciones de de Ithink®.
Antes de hacer el análisis de resultados se obtienen los promedios entre las 50 semanas para cada valor de A y B, promedios dados en cada variable por cada corrida. Por ejemplo si B=0.01 y A=0.05 (corrida 6 de 101 con sensitive), para la variable costo se toman los valores de las 50 semanas y se promedian, dando como resultado el valor PROM_Costos(A=0.05, B=0.01) (Ver Figura 14).
Para obtener los datos resultantes de Ithink®, estos se promediaron por corrida y se llevaron a la hoja de cálculo (Ver Figura 15).
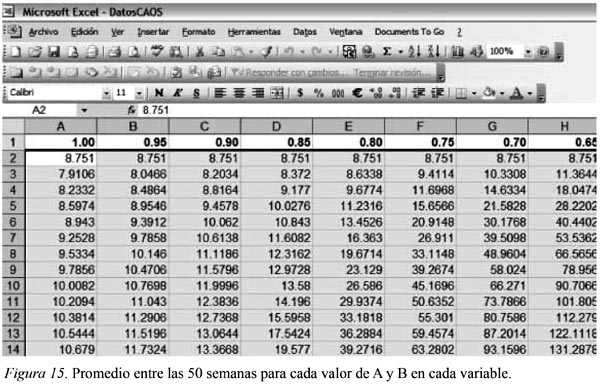
La totalidad de los datos se guardaron en un archivo temporal de Excel 2007®. Esto se guardó con el fin de obtener los promedios, para lo que se utilizó la función PROMEDIO sobre los datos de cada columna. Mediante la siguiente función en Matlab® se exportaron los datos de Excel para el análisis.
La capacidad gráfica del programa Matlab® se utiliza en los comandos de imagesc, que muestra los valores de la variable con un color particular o matiz de grises, el rojo o gris oscuro e indica valores grandes mientras que el azul o gris oscuro valores pequeños. Los comandos de surfc muestran una malla tridimensional junto con las curvas de nivel en el plano A,B para evaluar los valores de las variables gráficadas para un valor de A y B dados.
ANÁLISIS GRÁFICO PARA LA CARACTERIZACIÓN DEL CAOS
Existen dos maneras para identificar cuando un sistema es estable, periódico, cuasiperiódico o caótico. Estas se dan mediante métodos gráficos o mediante cuantificadores. Las gráficas o plots son visualmente eficientes para mostrar tendencias, patrones y comportamientos a partir de datos, de preferencia datos en gran cantidad.
Los gráficos pueden obtenerse a partir de series de tiempo, diagramas de fase, diagramas de fase-espacio o espectros de poder.Para el objeto del estudio se utiliza la simulación realizada en el modelo creado en ithink® y partir del análisis de sensibilidad, donde se pudieron variar los parametros A y B. Aquí se obtienen los resultados que no son nada más que miles de datos en cantidades según la variable que se analice.
En el programa Mathlab® se utilizan dos tipos de gráficas: una llamada imagesc de dos dimensiones con A y B en todo su rango como ejes. En la imagen se observa el área ocupada por los datos y el contorno que estos marcan en el plano. En este caso, los colores varían de azul oscuro, a amarillo y a rojo oscuro (o tonos de grises). Los azules (o grises oscuros) indican niveles bajos de unidades de variable; los amarillos (grises claros) niveles intermedios, y los rojos (grises oscuros) altos niveles de unidades de variable.
El otro tipo de gráfica utilizada es el surfc donde, con A y B en sus ejes Y y X y con las unidades de variable en el eje Z, se puede observar mejor la distribución de los datos y su comportamiento y variabilidad gracias a la adición del eje Z que permite tener una gráfica en 3D. Esta gráfica también muestra los contornos sobre el plano XY que las unidades de variable describen de acuerdo con su comportamiento. Los colores (o grises) exhibidos por la Figura 16 siguen los mismos parámetros de interpretación que los utilizados en la gráfica imagesc.
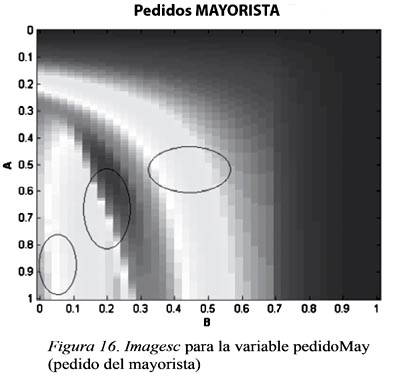
En la Figura 16 se observa un cambio brusco en los grises en la región A cercana a 1 y en los valores de B comprendidos entre 0.2 y 0.3 para los pedidos del mayorista (órdenes de unidades al distribuidor). Esto indica que al prestar más atención al inventario disponible que a lo que viene en la línea de suministro, en este caso A>B, se genera un cambio brusco en el comportamiento de las unidades que el mayorista ordenará para cambios ligeros en los parámetros. Es decir, el mayorista ordenará mucho más o mucho menos producto al distribuidor a partir de cambios no tan significativos en los parámetros de decisión. Las áreas de color negro, señaladas por las circunferencias, son las regiones donde el comportamiento caótico es evidente.
Para poder observar mejor estos comportamientos, se realiza una gráfica en tres dimensiones en esta región con Surfc entre 0 a 0.3 de la variable B. Vemos cómo hay un cambio significativo en el área demarcada por el recuadro en la Figura 17.
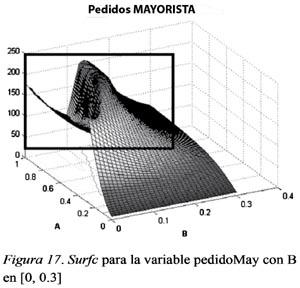
En la misma región observada en la Figura 17 se puede apreciar un comportamiento brusco en las unidades a ordenar por el distribuidor. Aquí el valor de la variable decae rápidamente en un intervalo muy pequeño en la región de los parámetros. De esta manera, por ejemplo, si se varía ligeramente el valor de B, como condición inicial del modelo, en los lugares con un valor pico (B entre 0.1 y 0.2), la cantidad de pedidos del mayorista cambiará drásticamente, dando lugar a un comportamiento caótico en esa región.
Con un A= 0.6 y un B= 0.1 en la simulación del modelo, el número de unidades a ordenar es un valor tope de 236.3704. Si el valor de B se substituye por 0.2, las unidades a ordenar disminuyen en un 48%, es decir, a un valor de 113.82, con tan solo un incremento del 10% en el parámetro de decisión tomando en cuenta las unidades del producto en tránsito. Es claro que con pequeños incrementos en los parámetros de decisión, se producen cambios significativos en las variables estudiadas, en este caso los pedidos del mayorista. (Figura 18)
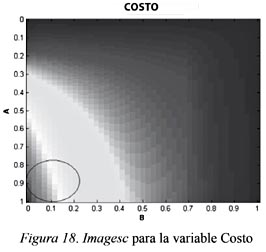
El comportamiento en los costos (el costo de mantener inventario) es estable y uniforme durante gran parte de la simulación. Sin embargo se identifica una región donde los cambios son significativos. Para valores de A cercanos a 1 y valores de B entre 0 y 0.2 se puede apreciar una variación en los colores (o tonos de grises) de la Figura 18. En la gráfica tridimensional de la Figura 19 se identifica un hundimiento en los costos y una zona donde estos decaen rápidamente.
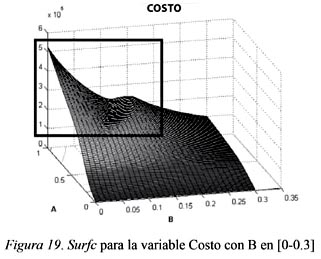
Las decisiones en los inventarios y en la línea de suministro afectan muy poco el comportamiento de los costos; tal vez se afecten en valores muy pequeños en cuanto a lo que viene en camino (B entre 0 y 0.15) En la gráfica se identifica un comportamiento descendente en los costos para la variableA=1 y los valores de B=[00.05], con pequeñas variaciones de B (ver Figura 20).
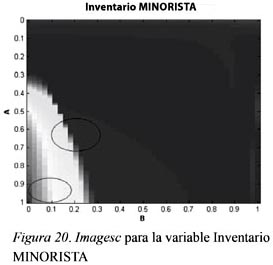
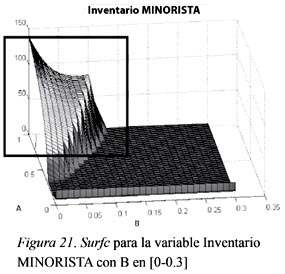
El inventario del minorista es el último nivel de la cadena. Este es el que suple la demanda externa y, como es de esperar, es una de las variables más susceptible de entrar en caos por todo lo que pueda ocurrir en los niveles previos (fábrica, distribuidor y mayorista). Sumado a esto están los parámetros A y B de decisión, que se observan en la Figura 20. Es obvio que estos tienen una gran inferencia en lo que pueda pasar con el comportamiento del inventario final que suministra la demanda externa.
En la Figura 21 se puede observar otro comportamiento tipo pared, para valores de decisión en la línea de suministro (B entre 0.05 y 0.15): una pequeña variación en estos valores resulta en un cambio brusco en inventario. Lo mismo ocurre para las decisiones en el inventario y su parámetro de decisión A: cuando A alcanza valores mayores a 0.3 y la decisión en la línea de suministro está entre 0 y 0.12, el inventario aumenta considerablemente.
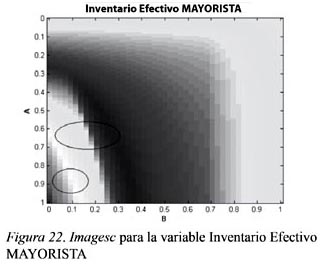
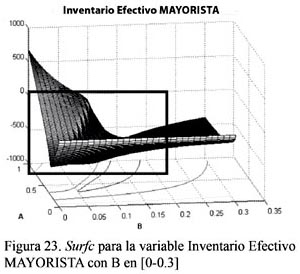
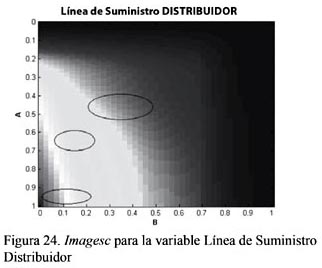
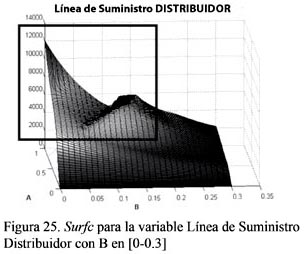
A continuación se mostrarán más gráficas Imagesc y Surfc para las otras variables analizadas: inventario efectivo del mayorista y línea de suministro del distribuidor, donde se señalan las regiones con comportamiento caótico (ver las Figuras del 22 al 25).
CONCLUSIONES
La cadena de suministro debe ser tratada como un sistema completo. Cualquier pequeño cambio que se haga para optimizar cualquier nivel en la cadena de suministros puede resultar en cambios significativos en otras partes dentro de la misma. Así vemos que cambios en A y B, que fueron los parámetros de decisión en este modelo, significaron alteraciones en niveles de inventarios, pedidos y costos.
En las graficas de dos y tres dimensiones existen momentos donde el sistema actuó caóticamente. Esta sensibilidad a las condiciones iniciales es la característica más importante de la Teoría del Caos y la cadena de suministro; como sistema, no es ajena a tal situación. En efecto, el uso de la Teoría del Caos aporta una base para describir e interpretar las interacciones dinámicas involucradas en la determinación de la estrategia a usar por los gerentes de operaciones y cadena de suministros. Los términos de condiciones iniciales, regiones inestables, aleatoriedad, complejidad, imprevisibilidad, entre otros, apoyan el desarrollo de un seguimiento coherente y significativo que ofrece descubrimientos muy valiosos en torno a las interacciones entre las cadenas de suministro, sus niveles y los sistemas de información. El estudio de las condiciones iniciales dentro de una cadena y su comportamiento, luego de ciertos estímulos, provee muchos indicios de por qué los fenómenos subsecuentes ocurren, y por qué el caos aparece.
Los parámetros A y B escogidos son los que, al variarse, generan caos en la cadena, como se pudo apreciar gráficamente. Éstos, como se explicó en el desarrollo del artículo, son valores que representan a la capacidad heurística utilizada por las personas encargadas de hacer los pedidos en cada nivel y determinan cuánto inventario o cuánto de lo que viene en tránsito se utilizará para cada caso en cada nivel.
En cualquier momento pueden ocurrir cambios dramáticos en el sistema sin previo aviso. Los cambios bruscos del inventario en los niveles de la cadena de suministros pueden ser generados por el sistema y no como resultado de eventos externos, tal como se aprecia en las gráficas de inventarios e inventarios efectivos del Mayorista.
Por otro lado, el software Ithink® no es lo suficientemente potente como para graficar los regímenes de caos, debido a la cantidad de datos que se manejan.
Por su parte, la opción de Sensi Specs permite variar sólo un parámetro automáticamente, el resto de las variaciones se deben realizar manualmente. No es recomendable para hacer análisis gráficos detallados, como se observó analizando los datos. El sistema Mathlab® se utiliza para visualizar la distribución de los mismos en el plano de los parámetros A y B y generar gráficas de superficie 3D. El uso de los colores (o matices de grises) y los contornos permitió identificar aquellas zonas donde las variables entraban en régimen de caos. Las cadenas de suministro no alcanzan un equilibrio constante, las perturbaciones en el sistema más pequeñas siempre van a dificultar la consecución de este equilibrio.
La simulación de los sistemas y el análisis de la dinámica no lineal, de acuerdo con el comportamiento de las variables más importantes dentro de una cadena, debe ser una parte fundamental de cualquier propuesta de reingeniería o mejoramiento para cualquier cadena de suministro.
RECOMENDACIONES
Para trabajos futuros se pueden utilizar cadenas con niveles múltiples, haciendo más compleja la simulación, aunque ampliando el campo de estudio del modelo. Este trabajo utilizó los valores de A y B comprendidos entre 0 y 1 como un solo conjunto de parámetros de decisión para todo el sistema en sus cuatro niveles. Para profundizar y acercarse a la realidad aún más, y así comprobar la existencia de regímenes de caos en las variables de la cadena de suministros, se recomienda variar estos valores dentro de cada nivel, lo equivalente para que cada nivel tenga su agente de decisión independiente.
REFERENCIAS
Special Issue: The Dynamics of Supply Chains and Networks. (2005). System Dynamics Review (Vol. 21). Norwich, Great Britain: Wiley.
Akkermans, H., & Dellaert, N. (2005). The Rediscovery of Industrial Dynamics: The Contribution of System Dynamics to Supply Chain Management in a Dynamic and Fragment World. System Dynamics Review, 21(3), 173-186.
Andersen, D. F., & Sturis, J. (1988). Chaotic Structures in Generic Management Models: Pedagogical Principles and Examples. System Dynamics Review, 4(1-2), 218-245.
Anderson Jr., E., Morrice, D. J., & Lundeen, G. (2005). The "physics" of Capacity and Backlog Management in Service and Custom Manufacturing Supply Chain. System Dynamics review, 217-247.
Chopra, S., & Meindl, P. (2008). Administración de la cadena de suministro. México: Pearson Educación.
Drew, S., Joe, B. H., & Jonathan, R. R. (2006). Enhancing Supply Chain Solutions with the Application of Chaos Theory. Supply Chain Management, 11(2), 108-114.
Forrester, J. W. (1971). Dinamica Industrial. Buenos Aires, Argentina: Ateneo.
Goncalves, P., Hines, J., & Sterman, J. (2005). The Impact of Endogenous Demand on Push-Pull Production Systems. System dynamics review, 187-216.
Hwarng, H. B., & Xie, N. (2008). Understanding Supply Chain Dynamics: A Chaos Perspective. European Journal of Operational Research, 184(3), 11631178.
Larsen, E. R., Morecroft, J. D. W., & Thomsen, J. S. (1999). Complex Behaviour in a Production-Distribution Model. European Journal of Operational Research, 119(1), 61-74.
Mosekilde, E., & Larsen, E. R. (1988). Deterministic Chaos in the Beer Production-Distribution Model. System Dynamics Review, 4(1-2), 131-147.
Paik, S. K., & Bagchi, P. K. (2007). Understanding the Causes of the Bullwhip Effect in a Supply Chain: International Journal of Retail & Distribution Management. Emerald Group Publishing Limited, 35(4), 308-322.
Sterman, J. D. (1989). Modeling Managerial Behavior: Misperceptions of Feedback in a Dynamic Decision Making Experiment. Management Science, 35(3), 321-339.
Sterman, J. D. (2000). Business Dynamics: Systems Thinking and Modeling for a Complex World. New York: Mc Graw Hill.
Recibido: 4 mayo, 2011
Aceptado: 7 julio, 2011