Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Journal of Economics, Finance and Administrative Science
Print version ISSN 2077-1886
Journal of Economics, Finance and Administrative Science vol.21 no.40 Lima June 2016
Article
Determining equivalent charges on flow and balance in individual account pension systems
Determinación de exacciones de efecto equivalente en el flujo y el balance de los sistemas de pensiones de cuentas individuales
Luis Chávez–Bedoya1
1Esan Graduate School of Business, Lima, Peru
Abstract
In this article, we determine a charge on balance that is equivalent to a certain fixed charge on flow for a particular utility–maximizer affiliate participating in a defined-contribution pension fund under the system of individual accounts. We also prove, under market completeness, that the equivalent charge on balance depends only on the current level of the charge on flow, the length of the accumulation period and the risk free rate of return.
Keywords: Pension fund. Defined benefit. Individual account. Charge on balance. Charge on flow.
Resumen
En este artículo se determina una exacción en el balance, que es equivalente a cierta tasa fija en el flujo de una empresa asociada particular maximizadora, que participa en un fondo de pensiones de aportación definida en el sistema de cuentas individuales. También se prueba, en la integridad del mercado, que la exacción de tipo equivalente en el balance depende solo del nivel actual de la tasa en el flujo, la duración del período de acumulación y un tipo de rentabilidad sin riesgo.
Palabras clave: Fondo de pensiones. Beneficio definido. Cuenta individual. Exacción en el balance. Exacción en el flujo.
1. Introduction
Two important characteristics of a defined–contribution (DC) pension fund are that affiliates borne the risk derived from fluctuations in the value of assets and that imposed administrative charges have a direct and significant impact on the terminal wealth of the corresponding individual account (IA). For example, Murthi, Orszag, and Orszag (2001) estimate that in the U.K. over 40% of the IA’s value is dissipated through fees and charges while Whitehouse (2001) determines that a levy of one per cent of assets adds up to nearly 20% of the final pension value. Administrative charges have also received a great deal of attention from the pension supervisory agencies, policy-makers and researchers, especially in countries that have partially or totally transformed their public defined-benefit pension systems into individual capitalization ones. The most familiar and documented example is Chile and the reader can find main aspects of such reform in Arrau, Valdés-Prieto, and Schmidt-Hebbel (1993), Diamond and Valdes-Prieto (1994), Edwards (1998), Arenas de Mesa and Mesa-Lago (2006). Also, Queisser (1998), Sinha (2000), Kay and Kritzer (2001), Mesa-Lago (2006), Kritzer, Kay, and Sinha (2011) and Marthans, J. and Stok, J. (2013) provide good references for the reform, situation and perspective of pension systems in Latin America.
As mentioned by Mitchell et al. (1998), James, Smalhout, and Vittas (2001) and Whitehouse (2001) the high charges of IA systems is one of their main criticisms since they discourage participation (as people consider contributions as taxes instead of savings), damage the reputation of the system, reduce future pensions, and increase future costs for the government whether there is guaranteed minimum pension. Devesa-Carpio, Rodríguez-Barrera, and Vidal-Meliá (2003) consider that the charge scheme adopted by the IA system is very important since fund accumulation process is exponential and targeted for long horizons. Following Kritzer et al. (2011), the most common administrative charges in IA pension systems are proportional on flow (or a percentage of the affiliate’s salary), fixed on flow, proportional on assets (balance) and proportional over excess returns. Analysis and comparison of administrative charges across different countries can be found in James et al. (2001), Whitehouse (2001), Devesa-Carpio et al. (2003), Corvera, Lartigue, and Madero (2006), Gómez-Hernandez and Stewart (2008), Tapia and Yermo (2008). Moreover, Sinha (2001), Masias and Sánchez (2007) and Martínez and Murcia (2008) analyze in detail the administrative charges in Mexico, Peru and Colombia, respectively.
However, this article will focus only on charges that are proportional on balance and flow since they are by far the most popular and important in Latin America1. Queisser (1998) considers that the charge on flow is more advantageous for the Pension Fund Administrator (PFA) in the initial stages of the system, and although the charge on balance aligns the PFA’s objectives in terms of increasing the fund’s profitability, it tends to be more expensive in the longrun as personal accounts grow in size. On the other hand, Shah (1997) mentions that the charge on flow generates distortions and undesirable tendencies like promoting high start-up costs for the PFAs, discouraging competition in the system and generating losses for older affiliates.
Asset allocation, performance and risk of a DC pension plan during its accumulation and decumulation phases have received a considerable attention in the literature. Blake, Cairns, and Dowd (2001) using different models for asset returns and portfolio strategies estimate the value-at-risk of the pension ratio. Poterba, Rauh, and Venti (2005) calculate the expected utility of retirement wealth for different investment strategies and assumptions. Devolder, Bosch Princep, and Domínguez Fabián (2003) derive several optimal portfolio strategies for different types of utility functions assuming the risky asset follows a geometric Brownian motion (GBM). Gao (2009) provides a similar analysis but under a constant elasticity variance (CEV) process for the risky assets. The efficiency of the mean-variance portfolio selection in a DC pension plan is studied in Vigna (2014) when the risky asset follows a GBM. Haberman and Vigna (2001) consider downside risk of an optimal asset allocation strategy derived from a discrete-time dynamic programming approach. Salary risk and inflation risk were incorporated in Battocchio and Menoncin (2004) and Han and Hung (2012) while maximizing the expected utility of terminal wealth. Battocchio, Menoncin, and Scaillet (2004) and Yang and Huang (2009) incorporate longevity risk in the optimal asset allocation of a DC plan; the former using as objective expected utility, and the latter deviation of terminal wealth with respect to a predetermined target. Stochastic lifestyling under terminal utility with habit formation is found and compared with other strategies in Cairns, Blake, and Dowd (2006). Finally, the reader interested in the analysis and optimal allocation during the decumulation phase can be referred, among others, to Blake et al. (2001), Gerrard, Haberman, and Vigna (2004), Horneff, Maurer, Mitchell, and Dus (2006) and Gerrard, Haberman, and Vigna (2006).
Nonetheless, methodologies to compare administrative charges in DC pension fund with IA during its accumulation period have not received that level of attention in the literature, especially in a continuous-time stochastic setting. Therefore, we fill such gap by developing a methodology, in the aforementioned environment, to determine equivalent charges on flow and balance. We consider a risk-averse affiliate who maximizes her expected utility of terminal wealth in a complete Black-Scholes market model2. Then, we determine the equivalent charges by equating the maximum terminal certainty equivalent that can be achieved under both kinds of charges. Moreover, under certain assumptions, we prove that the equivalent charges on balance and flow depend only on the length of the accumulation period and the risk-free rate of return; and, to the best of our knowledge this relationship between charges is new in the literature. This result is independent on the risky asset’s growth rate and volatility, as well as, the affiliate’s risk-aversion since the comparison of administrative charges can be performed by simple terminal wealth expectations under a risk-neutral probability measure.
The rest of the article proceeds as follows: Section 2 introduces a methodology to mathematically represent and compare charges on balance and flow. Section 3 discusses an application of the methodology to the Peruvian Private Pension System. Finally, Section 4 draws conclusions.
2. Methodology
Throughout this paper 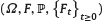 represents a filtered and complete probability space on which a standard
represents a filtered and complete probability space on which a standard 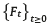 –adapted one-dimensional Brownian motion B(t) is defined. We denote by
–adapted one-dimensional Brownian motion B(t) is defined. We denote by 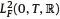 the set of all R -valued, measurable stochastic processes g(t) adapted to
the set of all R -valued, measurable stochastic processes g(t) adapted to 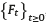 , such that
, such that 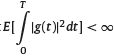 . For any
. For any 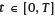 , we assume that the PFA can invest the affiliate’s contributions in only two assets which satisfy:
, we assume that the PFA can invest the affiliate’s contributions in only two assets which satisfy:
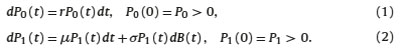
It is clear that r is the risk-free rate of return, and are the risky asset’s growth rate and volatility, respectively. The stochastic differential equation (SDE) in (2) generates a geometric Brownian motion (GBM) which is a common specification to model asset values and it is heavily utilized in stochastic control of DC pension funds as mentioned in the introduction. But most important, assets (1) and (2) generate a complete financial market and therefore it guarantees the existence of a risk-neutral probability measure. This property will be extremely useful to verify our theoretical results of Section 2.4.
2.1. The affiliate’s problem
Consider a particular PFA’s affiliate who has T > 0 months before retirement, i.e., T represents the length of her accumulation phase. She already has W0 > 0 ready to be invested in her individual account, and after that initial deposit she will contribute at a constant rate > 0 per month for the next T months. Also, for any 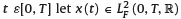 be the proportion of her IA that is invested in the risky asset. We also assume that the adjustments are performed instantly and free of charge. Let W(t) be the affiliate’s wealth in her IA at time t є [0, T]. If the PFA does not charge any administrative fees to the affiliate, then W(t) satisfies
be the proportion of her IA that is invested in the risky asset. We also assume that the adjustments are performed instantly and free of charge. Let W(t) be the affiliate’s wealth in her IA at time t є [0, T]. If the PFA does not charge any administrative fees to the affiliate, then W(t) satisfies
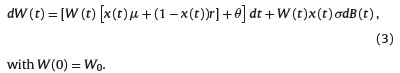
It is in the affiliate’s interest that the PFA will maximize her expected utility of terminal wealth, 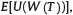 by determining an optimal proportion x* (t). We assume that U is strictly increasing, differentiable and concave in its domain. Therefore, the affiliate wants the PFA to solve problem (P) given by
by determining an optimal proportion x* (t). We assume that U is strictly increasing, differentiable and concave in its domain. Therefore, the affiliate wants the PFA to solve problem (P) given by

Following Vigna (2014), it is possible to find a closed-form expression for the value function and the optimal control under a general hyperbolic absolute risk aversion (HARA) class of utility functions. Because the main result of the paper regarding equivalent charges will be independent of risk-aversion, we choose for simplicity a particular case of the HARA class given by the exponential utility function.

The utility in (5) exhibits constant absolute risk aversion since 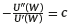 and it allows an explicit solution for (P). Following Devolder et al. (2003), the optimal proportion to be invested in the risky asset is
and it allows an explicit solution for (P). Following Devolder et al. (2003), the optimal proportion to be invested in the risky asset is
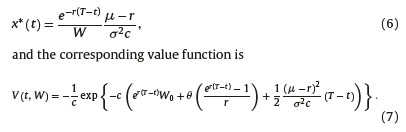
We can observe from (6) that the optimal control does not depend on the contribution rate θ. If we apply the optimal strategy x*(t) stated in (6), then 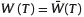 and the maximum expected utility of terminal wealth is
and the maximum expected utility of terminal wealth is
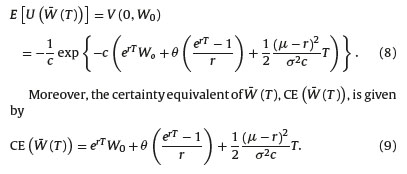
As we can notice from (9), 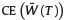 is the sum of the future value of W0, the future value of a continuous annuity with rate θ (both using the risk-free rate r) and a term depending on the market price of risk and the risk aversion parameter but independent of any contribution made to the IA. Next, we describe in detail the charges that the PFA will apply either on the affiliate’s IA or on her contributions. We will use a structure similar to the one considered in Shah (1997), Diamond (2000), Blake and Board (2000), Whitehouse (2001), Devesa-Carpio et al. (2003) and Gómez-Hernández and Stewart (2008).
is the sum of the future value of W0, the future value of a continuous annuity with rate θ (both using the risk-free rate r) and a term depending on the market price of risk and the risk aversion parameter but independent of any contribution made to the IA. Next, we describe in detail the charges that the PFA will apply either on the affiliate’s IA or on her contributions. We will use a structure similar to the one considered in Shah (1997), Diamond (2000), Blake and Board (2000), Whitehouse (2001), Devesa-Carpio et al. (2003) and Gómez-Hernández and Stewart (2008).
2.2. Charge on balance
Let 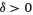 be the monthly charge on balance expressed in continuous time. It is also known as charge on assets or on stock and, in general, it is applied as a percentage of the value of assets under management. The affiliate wants to study the value of her IA under this type of charge. If we denote such wealth as Ws(t), it will satisfy the following SDE
be the monthly charge on balance expressed in continuous time. It is also known as charge on assets or on stock and, in general, it is applied as a percentage of the value of assets under management. The affiliate wants to study the value of her IA under this type of charge. If we denote such wealth as Ws(t), it will satisfy the following SDE
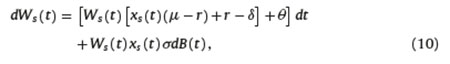
with Ws (0) = W0. Notice that the charge on balance will diminish the monthly growth rates µ and r by a quantity equal to ξ.We will use a control xs(t) to indicate the fraction of the IA invested in the risky asset under the charge on balance. In this case, the affiliate wants to solve problem (Ps) given by

Notice that the last term of (12) does not depend on the initial contribution (W0), the charge on balance (ξ), and the contribution rate (θ). Next, we describe the charge on flow.
2.3. Charge on flow
Let α>0 be the charge on flow and it could be applied as a fraction of the affiliate’s salary or contributions. Whether the affiliate makes a contribution X in a particular month, we assume the charge she will pay to the PFA (at the moment the contribution is made) will be 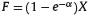 . Considering that F could have been invested in the fund, it is possible to express contribution X as
. Considering that F could have been invested in the fund, it is possible to express contribution X as 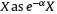 when adjusted for the opportunity cost of F. In the case of a constant rate of contribution, θ, the charge on flow will generate an adjusted contribution rate of
when adjusted for the opportunity cost of F. In the case of a constant rate of contribution, θ, the charge on flow will generate an adjusted contribution rate of 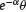 .
.
The affiliate wants to study the value of her individual account under this type of charge. We denote such wealth as Wf (t) and it will satisfy the following SDE:
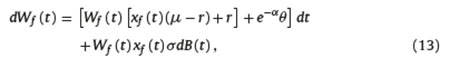
with 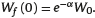 . Recall that Wf (T) does not represent the "true" wealth of the affiliate at the end of the accumulation phase but the final wealth adjusted by the opportunity cost of the charge on flow. Then, random variablesWf (T) andWs(T) can be compared.
. Recall that Wf (T) does not represent the "true" wealth of the affiliate at the end of the accumulation phase but the final wealth adjusted by the opportunity cost of the charge on flow. Then, random variablesWf (T) andWs(T) can be compared.
We will use a control xf (t) to indicate the fraction of the IA invested in the risky asset under the charge on flow. Thus, the affiliate wants to solve the problem (Pf) given by
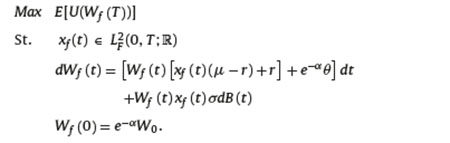
Based on the previous results and assumptions regarding the exponential utility function, the optimal control and the maximum certainty equivalent of (Pf) are
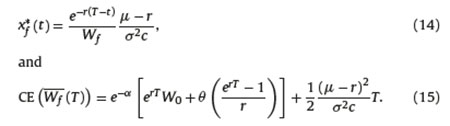
Similar to (12), only the last term of (15) depends only on the market price of risk 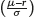 , the risk aversion parameter (c) and the length of the accumulation period.
, the risk aversion parameter (c) and the length of the accumulation period.
2.4. Comparing charges on balance and flow
The affiliate wants to compare her optimal expected utility of adjusted terminal wealth under the two types of charges considered. Therefore, it is appropriate to contrast both 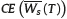 and
and 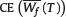 given by (12) and (15), respectively. Moreover, we define the following ratio to establish such comparison
given by (12) and (15), respectively. Moreover, we define the following ratio to establish such comparison

If Rsf > 1, the charge on balance will be preferred. If Rsf < 1 the charge on flow will be preferred. Finally, when Rsf = 1 the affiliate will be indifferent between both schemes.
We will consider W0 = 0, i.e., the accumulation phase begins with an amount equal to zero in the affiliate’s individual account. Under this assumption and considering all the other variables fixed, we can express ratio Rsf in (16) as a function of the charge on balance ξ. For the exponential utility function we have:
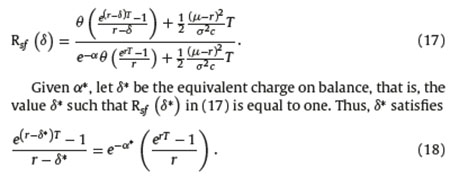
The left-hand side of (18) is the future value at T of a continuous annuity with unit rate and interest r − ξ*. The right-hand side corresponds to the future value at T of a continuous annuity with rate 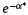 and interest r. If we denote the future values of such annuities as
and interest r. If we denote the future values of such annuities as 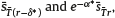 , then (18) is equivalent to
, then (18) is equivalent to 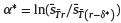 . Moreover, we can observe that ξ* will depend only on r, T and α*. Hence, it is independent of the parameters µ and σ of the risky asset, the contribution rate and the risk aversion coefficient c. Finally, notice from (18) that if T and r increases then ξ* decreases, improving the relative performance of the charge on flow with respect to the charge on balance.
. Moreover, we can observe that ξ* will depend only on r, T and α*. Hence, it is independent of the parameters µ and σ of the risky asset, the contribution rate and the risk aversion coefficient c. Finally, notice from (18) that if T and r increases then ξ* decreases, improving the relative performance of the charge on flow with respect to the charge on balance.
In the next section we generalize equation (18) for any riskaverse affiliate as described in Section 2.1.
2.5. Equivalent charges in a complete market
As mentioned before, the financial market consisting of the riskfree asset and the risky asset given by (1) and (2) is complete. Also, given 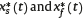 , the optimal controls of problems (Ps) and (Pf), we can determine both
, the optimal controls of problems (Ps) and (Pf), we can determine both 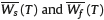 . The equivalent charges of flow and balance can be obtained by comparing the expected present values of their corresponding IAs under the risk-neutral probability measure Q. For that purpose we define the ratio Nsf as:
. The equivalent charges of flow and balance can be obtained by comparing the expected present values of their corresponding IAs under the risk-neutral probability measure Q. For that purpose we define the ratio Nsf as:

The ratio in (19) is equivalent to the expected present values of 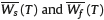 using probability measure Q since the factor
using probability measure Q since the factor 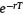 appears in both numerator and denominator of (19). Additionally, if Nsf > 1, the charge on balance will be preferred. If Nsf < 1 the charge on flow will be preferred; and, when Nsf = 1 the affiliate will be indifferent between both schemes.
appears in both numerator and denominator of (19). Additionally, if Nsf > 1, the charge on balance will be preferred. If Nsf < 1 the charge on flow will be preferred; and, when Nsf = 1 the affiliate will be indifferent between both schemes.
It is clear that both 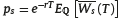 and pf =
and pf = 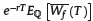 represent the current prices of the affiliate’s IA accounts under the corresponding charges. For example, ps is the amount of money that the affiliate will receive today in exchange of giving her IA (entirely) at the end of the accumulation phase, in this case it is assumed that the charge is on balance, and that she will continue to contribute to the fund at a rate θ until T.
represent the current prices of the affiliate’s IA accounts under the corresponding charges. For example, ps is the amount of money that the affiliate will receive today in exchange of giving her IA (entirely) at the end of the accumulation phase, in this case it is assumed that the charge is on balance, and that she will continue to contribute to the fund at a rate θ until T.
Under Q both the risk free rate and the risky assets grow at a rate r, then for fixed charges α and ξ we have:
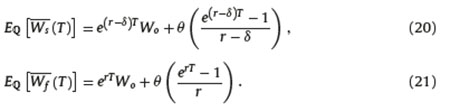
Given 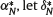 be the equivalent charge on balance, that is, the value
be the equivalent charge on balance, that is, the value 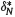 such that
such that 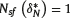 . Then, it is easy to verify that
. Then, it is easy to verify that 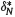 also satisfies equation (18) when W0 = 0. This framework is far more general than the particular case of the exponential utility function because the comparison of administrative charges performed through the ratio Nsf will be valid for any risk-averse affiliate.
also satisfies equation (18) when W0 = 0. This framework is far more general than the particular case of the exponential utility function because the comparison of administrative charges performed through the ratio Nsf will be valid for any risk-averse affiliate.
3. Numerical application
In this section, we present an application of the proposed methodology to the Peruvian Private Pension System. This application is relevant because the PPS is going through an important reform exactly 20 years after its creation. Part of the reform consists of replacing the charge on flow with a charge on balance, and this situation has partially motivated the present research article3.
We consider a retirement age of 65 years and ignore the mandatory insurance fee. We will work with three charges on flow (expressed as percentages of the affiliate’s salary): fmin = 1.47%, fmax = 1.69%, and favg = 1.58% which corresponds to the minimum, maximum and average PPS’s charges on flow as in May 2014. Since dependent workers in Peru have a mandatory contribution of 10% of salary and fi are applied to it, we have αi = −ln(1 − 10fi) and therefore αmin = 0.1590, αmax = 0.185 and αavg = 0.172. We will also assume that monthly risk-free is r = 0.037%, and it was estimated using the inflation-adjusted Peruvian bonds with maturity 30 days. The data series consists on daily observations of the corresponding yearly rate from 20/12/2005 to 16/05/2014.
Table 1 and Figure 1 show 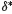 (annualized) for certain ages4 and three scenarios for the charge on flow: fmin, fmax and favg. As expected from (18), we observe that
(annualized) for certain ages4 and three scenarios for the charge on flow: fmin, fmax and favg. As expected from (18), we observe that  is strictly increasing in age (decreasing in T), and strictly decreasing in f for a fixed T. In the case of a 40-year-old affiliate, or equivalently T = (65 − 40) × 12 = 300 months,
is strictly increasing in age (decreasing in T), and strictly decreasing in f for a fixed T. In the case of a 40-year-old affiliate, or equivalently T = (65 − 40) × 12 = 300 months,  is 1.398% per year when favg is the corresponding charge on flow. This implies that a charge on balance smaller than 1.398% makes such scheme convenient for the 40-year-old affiliate. The corresponding values for fmin and fmax are 1.289% and 1.510% per year, respectively. An important age to consider is 37 years since half of PPS’s affiliates are younger than that age. The corresponding
is 1.398% per year when favg is the corresponding charge on flow. This implies that a charge on balance smaller than 1.398% makes such scheme convenient for the 40-year-old affiliate. The corresponding values for fmin and fmax are 1.289% and 1.510% per year, respectively. An important age to consider is 37 years since half of PPS’s affiliates are younger than that age. The corresponding  for favg is 1.245% per year. Consequently, if the charge on flow is the system’s average (or 1.58% of salary) and the charge on balance is greater than 1.245% per year, then the youngest half of the affiliates in the system will find the charge on balance undesirable.
for favg is 1.245% per year. Consequently, if the charge on flow is the system’s average (or 1.58% of salary) and the charge on balance is greater than 1.245% per year, then the youngest half of the affiliates in the system will find the charge on balance undesirable.
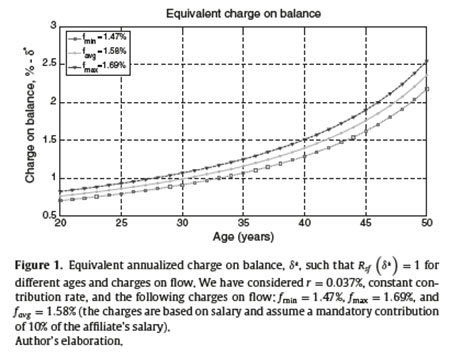
We can observe that 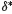 ≥ 0.704% for all cases considered in the example, and such level would make the charge on balance to be preferred for almost all PPS’s affiliates. Recall that we are considering r = 0.037%; however, an increment in r will make the values of
≥ 0.704% for all cases considered in the example, and such level would make the charge on balance to be preferred for almost all PPS’s affiliates. Recall that we are considering r = 0.037%; however, an increment in r will make the values of 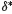 smaller and therefore the charge on balance will become less attractive.
smaller and therefore the charge on balance will become less attractive.
4. Conclusions and further research
We have developed a methodology to determine equivalent charges on flow and balance for individual account pension systems. We have considered a risk-averse affiliate who wants to maximize her expected utility of adjusted terminal wealth in acomplete financial market. Then, we need to solve the corresponding stochastic control problems to find and compare the maximum terminal certainty equivalent (CE) which can be achieved under both charge schemes. Under a fixed contribution rate, an exponential utility function and no initial amount in the IA, we are able to find the equivalent charges (those whichmakeboth schemes indifferent in terms of terminal CE) by solving a nonlinear equation involving only the future values of two continuous annuities. Moreover, the results will hold for any utility function and investment strategy since market completeness allows us to work in a risk-neutral environment.
The methodology was applied to the Peruvian Private Pension System (PPS) in order to determine the equivalent charge on balance for different accumulation horizons and three scenarios for the charge on flow. We found that a charge on balance lower than 0.704% per year would make such scheme preferable to the one based on flow for almost all PPS’s affiliates. However, such threshold assumes a monthly risk-free rate of 0.037%, a constant contribution rate and a fixed charge on flow greater than 1.47% of the affiliate’s salary. It is possible to extend this methodology to consider a time-varying contribution rate, risk-free rate and charge on balance, as well as other modifications preserving market completeness. Finally, it will be worth to perform a complete analysis in a general equilibrium environment considering a welfare target; but, this is beyond the scope of the paper.
References
Arenas de Mesa, A. & Mesa-Lago, C. (2006). The structural pension reform in Chile: Effects, comparisons with other Latin American reforms, and lessons. Oxford Review of Economic Policy, 22(1), 149–167. [ Links ]
Arrau, P., Valdés-Prieto, S. & Schmidt-Hebbel, K. (1993). Privately managed pension systems: Design issues and the Chilean experience. Washington DC: Technical report, World Bank. [ Links ]
Battocchio, P., Menoncin, F. & Scaillet, O. (2004). Optimal asset allocation for pension funds under mortality risk during the accumulation and decumulation phases. Annal of Operations Research, 152(1), 141–165. [ Links ]
Blake, D. & Board, J. (2000). Measuring value added in the pensions industry. Geneva Papers on Risk and Insurance-Issues and Practice, 25(4), 539–567. [ Links ]
Blake, D., Cairns, A. J. G. & Dowd, K. (2001). Pensionmetrics: Stochastic pension plan design and value-at-risk during the accumulation phase. Insurance: Mathematics and Economics, 29(2), 187–215. [ Links ]
Cairns, A. J. G., Blake, D. & Dowd, K. (2006). Stochastic lifestyling: Optimal dynamic asset allocation for defined contribution pension plans. Journal of Economic Dynamics and Control, 30(5), 843–877. [ Links ]
Corvera, F., Lartigue, J. & Madero, D. (2006). Análisis comparativo de las comisiones por administración de los fondos de pensiones en los países de América Latina. Mexico City: Mimeo. [ Links ]
Devesa-Carpio, J., Rodríguez-Barrera, R. & Vidal-Meliá, C. (2003). Medición y comparación internacional de los costes de administración para el afiliado en las cuentas individuales de capitalización. Revista Española de Financiación y Contabilidad. XXXII, 116, 95–144. [ Links ]
Devolder, P., Bosch Princep, M. & Domínguez Fabián, I. (2003). Stochastic optimal control of annuity contract. Insurance: Mathematics and Economics, 33(2), 227–238. [ Links ]
Diamond, P. (2000). Administrative costs and equilibrium charges with individual accounts. In J. B. Shoven (Ed.), Pages 137-172 of: Administrative aspects of investment-based social security reform (pp. 137–172). University of Chicago Press. [ Links ]
Diamond, P. & Valdés-Prieto, S. (1994). Social security reforms. In B. Bosworth, R. Dornbusch, & R. Laban (Eds.), The Chilean economy: Policy lessons and challenges (pp. 257–328). Washington DC: Brookings Institution. [ Links ]
Edwards, S. (1998). The Chilean pension reform: A pioneering program. In M. Feldstein (Ed.), Privatizing social security (pp. 33–62). University of Chicago Press. [ Links ]
Gao, J. (2009). Optimal portfolios for DC pension plans under a CEV model. Insurance: Mathematics and Economics, 44(3), 479–490. [ Links ]
Gerrard, R., Haberman, S. & Vigna, E. (2004). Optimal investment choices post retirement in a defined contribution pension scheme. Insurance: Mathematics and Economics, 35(2), 321–342. [ Links ]
Gerrard, R., Haberman, S. & Vigna, E. (2006). The management of decumulation risk in a defined contribution pension plan. North American Actuarial Journal, 10(1), 84–110. [ Links ]
Gómez-Hernández, D. & Stewart, F. (2008). Comparison of costs and fees in countries with private defined contribution pension systems. Paris: Working paper 6. International Organisation of Pension Supervisors. [ Links ]
Haberman, S. & Vigna, E. (2001). Optimal investment strategies and risk measures in defined contribution pension schemes. Insurance: Mathematics and Economics, 31(1), 35–69. [ Links ]
Han, N. & Hung, M. (2012). Optimal asset allocation for DC pension plans under inflation. Insurance: Mathematics and Economics, 51(1), 172–181. [ Links ]
Horneff, J., Maurer, R., Mitchell, S. & Dus, I. (2006). Optimizing the retirement portfolio: Asset allocation, annuitization, and risk aversion. Technical report National Bureau of Economic Research. [ Links ]
James, E., Smalhout, J. & Vittas, D. (2001). Administrative costs and the organization of individual retirement account systems: a comparative perspective. World Bank Policy Research Working Paper 2554. [ Links ]
Kay, S. & Kritzer, B. (2001). Social security in Latin America: Recent reforms and challenges. Federal Reserve Bank of Atlanta Economic Review, 86(1), 41–52. [ Links ]
Kritzer, B., Kay, S. & Sinha, T. (2011). Next generation of individual account pension reforms in Latin America. Social Security Bulletin, 71(1), 35–76. [ Links ]
Marthans, J. & Stok, J. (2013). Una propuesta para reformar los sistemas privados de pensiones: el caso peruano. Documento de trabajo, Universidad de Piura. [ Links ]
Martínez, O. & Murcia, A. (2008). Sistema de comisiones de las administradoras de fondos de pensiones en Colombia. Reporte de estabilidad financiera, Banco de la República de Colombia. [ Links ]
Masias, L. & Sánchez, E. (2007). Competencia y reducción de comisiones en el sistema privado de pensiones: el caso peruano. Documento de Trabajo. Superintendencia de Banca, Seguros y Administradoras de Fondos de Pensiones (SBS). [ Links ]
Mesa-Lago, C. (2006). Private and public pension systems compared: An evaluation of the Latin American experience. Review of Political Economy, 18(3), 317–334. [ Links ]
Murthi, M., Orszag, J. M. & Orszag, P. R. (2001). Administrative costs under a decentralized approach to individual accounts: Lessons from the United Kingdom. In R. Holzmann & J. Stiglitz (Eds.), New ideas about old age security (pp. 308–335). The World Bank. [ Links ]
Poterba, J., Rauh, J. & Venti, S. (2005). Utility evaluation of risk in retirement saving accounts. In D. A. Wise (Ed.), Analyses in the economics of aging (pp. 13–58). University of Chicago Press. [ Links ]
Queisser, M. (1998). Regulation and supervision of pension funds: Principles and Practices. International Social Security Review, 51(2), 39–55. [ Links ]
Shah, H. (1997). Towards better regulation of private pension funds. World Bank Paper 1791. [ Links ] Sinha, T. (2000). Pension reform in Latin America and its lessons for international policymakers. Kluwer Academic Pub 23. [ Links ]
Sinha, T. (2001). Analyzing management fees of pension funds: A case study of Mexico. Journal of Actuarial Practice, 9, 5–43. [ Links ]
Tapia, W. & Yermo, J. (2008). Fees in individual account pension systems: A crosscountry comparison OECD Working Papers on Insurance and Private Pensions 27. OECD Publishing. [ Links ]
Vigna, E. (2014). On efficiency of mean-variance based portfolio selection in defined contribution pension schemes. Quantitative Finance, 14(2), 237–258. [ Links ]
Whitehouse, E. (2001). Administrative charges for funded pensions: comparison and assessment of 13 countries. In Private pension systems: Administrative costs and reforms. pp. 85–154. OECD. [ Links ]
Yang, S. & Huang, H. (2009). The impact of longevity risk on the optimal contribution rate and asset allocation for defined-contribution pension plans. The Geneva Papers on Risk and Insurance-Issues and Practice, 34(4), 660–681. [ Links ]
E-mail address: lchavezbedoya@esan.edu.pe
Received 17 July 2014
Accepted 14 March 2016
NOTAS DE PIE
1 On the one hand, Bolivia, Colombia, Chile, El Salvador, Peru, and Uruguay have charges on flow. On the other hand, Mexico, Bolivia, Costa Rica, and Uruguay have charges on assets. Notice that in Bolivia and Peru both type of charges coexist.
2 This market consists on a risky asset following a geometric Brownian motion and a risk-free asset. Both assets can be traded continuously and frictionless.
3 Peruvian Law No.29903 contains the main aspects of the reform. One is that affiliates will migrate to a mixed charge that has a 10-year transient flow component, and from year 10 onwards the charge will be only on balance. The reform also includes a bidding mechanism on charges to allocate new affiliates and norms to incorporate independent workers.
4 If E is the affiliate’s age, then T = (65 − E) × 12 months will be the length of the accumulation phase.