Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista Digital de Investigación en Docencia Universitaria
versión On-line ISSN 2223-2516
Rev. Digit. Invest. Docencia Univ. vol.11 no.1 Lima ene./jun. 2017
http://dx.doi.org/10.19083/ridu.11.486
ARTÍCULO METODOLÓGICO
Aproximación conceptual y práctica a los Modelos de Ecuaciones Estructurales
Conceptual and Practical Approach to Structural Equations Modeling
Aproximação conceitual e prática aos modelos de equações estruturais
Leonardo Adrián Medrano* (http://orcid.org/0000-0002-3371-5040)
Roger Muñoz-Navarro** (http://orcid.org/0000-0002-7064-3699)
* Facultad de Psicología, Universidad Siglo 21, Córdoba, Argentina
** Facultad de Psicología, Universidad de Valencia, Valencia, España
RESUMEN
En el presente trabajo se expone una aproximación conceptual y práctica a los Modelos de Ecuaciones Estructurales o Structural Equation Modeling (SEM). Los SEM están considerados entre las herramientas más potentes para el estudio de relaciones causales en datos no experimentales. Son una combinación del análisis factorial y la regresión múltiple y están compuestos por dos componentes: el modelo de medida y el modelo estructural. El modelo de medida describe la relación existente entre una serie de variables observables; mientras que en el modelo estructural se especifican las relaciones hipotetizadas entre las variables, es decir, se describen las relaciones entre las variables latentes mediante el uso de flechas. Llevar a cabo un SEM involucra cinco etapas: 1) Especificación del Modelo; 2) Identificación del Modelo; 3) Estimación del Modelo; 4) Evaluación del Modelo y 5) Re-especificación del Modelo. El presente artículo provee una serie de guías de "buenas prácticas" para realizar análisis SEM, con ejemplos utilizando el programa AMOS.
Palabras clave: Modelos de Ecuaciones Estructurales, AMOS, análisis factorial, regresión múltiple
ABSTRACT
This methodological article explains a conceptual and practical approach to Structural Equation Models or Structural Equation Modeling (SEM). SEMs are considered among the most powerful tools for the study of causal relationships in non-experimental data. They are a combination of factor analysis and multiple regression and are composed of two components: the measurement model and the structural model. The measurement model describes the relationship between a series of observable variables; while in the structural model the relationships between variables are hypothesized; i.e., the relationships between latent variables are described with the use of arrows. Performing a SEM involves five stages: 1) A specification of the Model; 2) Identification of the Model; 3) Estimation of the Model; 4) Evaluation of the Model and 5) Re-specification of the Model. This article provides a series of guidelines on "best practices" for SEM analysis, with examples using the AMOS program.
Key words: Structural Equation Modeling, AMOS, factor analysis, multiple regression
RESUMO
Neste trabalho expõe-se uma aproximação conceitual e prática aos Modelos de Equações Estruturais ou Structural Equation Modeling (SEM). Os SEM estão considerados entre as ferramentas mais potentes para o estudo de relações causais em dados não experimentais. São uma combinação da análise fatorial e a regressão múltipla e têm dois componentes: o modelo de medida e o modelo estrutural. O modelo de medida descreve a relação existente entre uma série de variáveis observáveis; enquanto que no modelo estrutural especificam-se as relações hipotéticas entre as variáveis; ou seja, descrevem-se as relações entre as variáveis latentes através do uso de conjuntos. Realizar um SEM envolve cinco etapas: 1) Especificação do modelo; 2) Identificação do modelo; 3) Estimativa do modelo; 4) Avaliação do Modelo e 5) Reespecificação do Modelo. Este artigo fornece uma série de guias de "boas práticas" para realizar SEM com exemplos utilizando o programa AMOS.
Palavras-chave: Modelos de equações estruturais, AMOS, análise fatorial, regressão múltipla
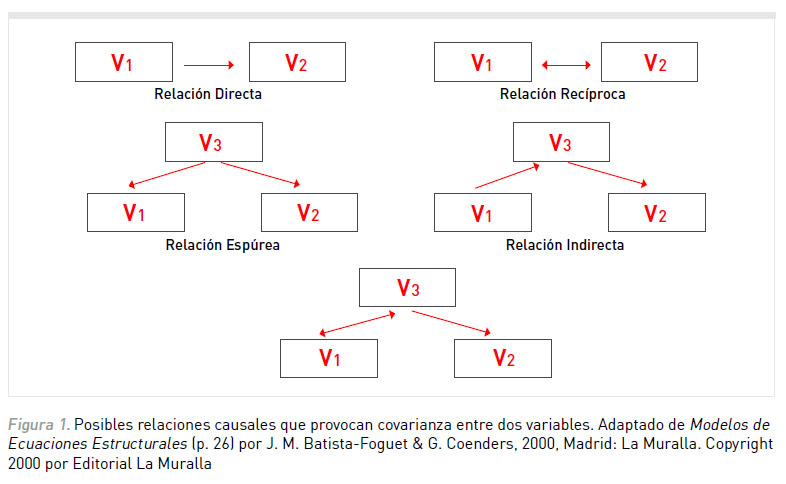
Inferir la existencia de una relación causal a partir de una correlación supone un error lógico. La covariación entre dos variables solo indica que los cambios de una variable (V1) se dan al mismo tiempo que los cambios en otra variable (V2). Por el contrario, en una relación causal se supone que todo cambio en una de las variables (causa), necesariamente provocará una variación en la otra (efecto). Por lo cual, para inferir que V1 sea causa de V2, además de la covariación entre las mismas es necesario establecer la dirección (si V1 antecede a V2) y el aislamiento de la relación (descartar causas alternativas de los cambios en V2).
En la investigación experimental es posible evaluar si una variable antecede a la otra manipulando la variable independiente, y controlando la influencia de variables alternativas mediante el uso del control experimental (León & Montero, 2003). En la investigación no experimental, por el contrario, no es posible garantizar la direccionalidad y aislamiento de una relación, ya que no existe manipulación ni control experimental. Sumado a ello, debe considerarse que frente a la covarianza de dos variables pueden establecerse diferentes direcciones o tipos de relaciones causales (ver Figura 1).
Frente a esta situación cabe preguntarse: ¿es posible analizar la existencia de relaciones causales en diseños no experimentales? La respuesta no es simple, ni se encuentra libre de controversia. Sin embargo, existe acuerdo en la comunidad científica al considerar que los Modelos de Ecuaciones Estructurales (Structural Equation Modeling; SEM) constituyen la metodología más potente y adecuada para analizar la plausibilidad de una relación causal, aun cuando se estén utilizando diseños no experimentales. La clave de esta metodología consiste en analizar la viabilidad de una dirección causal y sustituir el control experimental por un control estadístico, permitiendo así un seudoaislamiento de las variables en estudio.
El número de trabajos científicos que apelan al uso de SEM ha crecido de manera sostenida, sin embargo, también se observa un uso inadecuado de esta metodología (Jackson, Gillaspy & Purc-Stephenson, 2009). Diferentes revisiones sistemáticas indican problemas recurrentes en los trabajos con SEM, como, por ejemplo, no examinar los supuestos de normalidad, no reportar todos los parámetros involucrados, considerar un único índice de ajuste u obviar información sobre el método de estimación utilizado (DiStefano & Hess, 2005; MacCallum & Austin’s, 2000).
El presente artículo tiene por objetivo presentar una aproximación conceptual y práctica a los SEM. Si bien en la literatura científica abundan trabajos sobre esta metodología de análisis (Bagozzi & Yi, 2011; Iacobucci, 2009; Martens & Haase, 2006), son pocos los artículos en castellano que brindan una explicación clara y simplificada que permita a lectores no especializados introducirse en este tema. De esta manera se pretende brindar una aproximación al SEM más centrada en la explicación de la lógica subyacente, que en sus fundamentos matemáticos. Asimismo, se intentará describir de manera simple y didáctica los pasos implicados en la realización de SEM mediante el uso del programa AMOS. A partir de ello nos proponemos: (a) explicar los fundamentos conceptuales y lógicos del SEM; (b) describir los pasos principales del método utilizando el software AMOS, y (c) brindar una guía de buenas prácticas en el reporte de información para trabajos que utilicen SEM. Se espera así brindar a los lectores una serie de pautas que orienten el proceso de toma de decisiones implicados en el SEM.
LÓGICA SUBYACENTE DE LOS MODELOS DE ECUACIONES ESTRUCTURALES
Los SEM son considerados las herramientas más potentes para el estudio de relaciones causales en datos no experimentales (Aron & Aron, 2001). No obstante, a pesar de su sofisticación dichos modelos no prueban la causalidad, solo permiten seleccionar hipótesis causales relevantes y desechar aquellas no soportadas por la evidencia empírica. De esta manera, y siguiendo un principio falsacionista, las teorías causales son susceptibles de ser estadísticamente rechazadas si se contradicen con los datos observados.
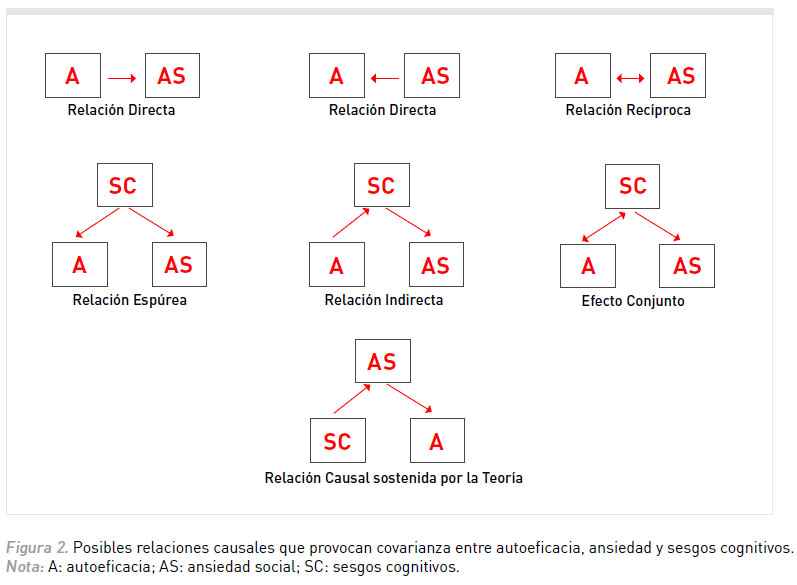
El análisis de ecuaciones estructurales parte de la siguiente premisa: las covarianzas pueden proporcionar información sobre las relaciones causales. Aunque la existencia de covarianza brinda información insuficiente, dado que existe una multitud de efectos posibles que pueden provocarla (ver Figura 1), se considera que es posible dilucidar la causalidad mediante el uso del control estadístico y la selección de efectos guiada por criterios teóricos. La lógica subyacente consiste en descomponer la covarianza entre las variables para obtener información sobre los parámetros del proceso causal subyacente. De esta manera, utilizando reglas de descomposición y seleccionando posibles fuentes de covariación, se establece de forma intuitiva la relación entre los parámetros y las covariaciones. Por ejemplo, si se observa covarianza entre ansiedad (A) y autoeficacia social (AS), esta relación podría deberse a que la ansiedad influye sobre la autoeficacia social, que la autoeficacia social influye sobre la ansiedad o que otras variables están afectando la covariación entre las mismas (por ejemplo, un sesgo cognitivo; SC). Dado que existen muchas relaciones causales que podrían explicar la covarianza entre A y AS (ver Figura 2), por medio de criterios teóricos se elige uno de los posibles nexos causales. Por ejemplo, un modelo que plantea que los sesgos cognitivos afectan la autoeficacia social y esto aumenta la ansiedad.
Es importante destacar que, aunque resulte atractivo establecer una relación causal, los análisis mediante SEM no proporcionan evidencias suficientes para "demostrar" la existencia de una relación causal. A pesar de su sofisticación los análisis basados en SEM no son otra cosa que estimaciones sobre la base de datos transversales. Solo los diseños experimentales con grupo control y asignación aleatoria brindan suficientes garantías para corroborar una relación causal (Ruiz, Pardo & San Martin, 2010). No obstante, los diseños SEM sí permiten "contrastar" hipótesis causales, ya que de no corroborarse el ajuste del modelo se puede descartar la hipótesis causal propuesta.
Una vez seleccionada la posible relación causal entre las variables, se procede a estimar los parámetros de la relación considerando las reglas de descomposición de la varianza y utilizando métodos de estimación (máxima probabilidad, por ejemplo).
Básicamente existen dos reglas de descomposición: (1) la covarianza entre dos variables es igual a la suma de los efectos directos, indirectos, espurios y conjuntos; y (2) la varianza de una variable dependiente es igual a la varianza debida a la perturbación, más la varianza explicada por otras variables del modelo. Mediante el uso de dichas reglas se construye un sistema de ecuaciones estructurales que expresa cada elemento de la matriz de covarianza en función de los parámetros del modelo. En otras palabras, dichas ecuaciones imponen una forma o estructura determinada a la matriz de varianza y covarianza de la población bajo estudio (Batista-Foguet & Coenders, 2000). La lógica del SEM sería que: es posible derivar las medidas de covariación esperadas entre las variables a partir de los efectos causales que se especifican en el modelo. De esta forma, si el modelo causal que se propone es correcto, las medidas de covariación esperadas y las observadas deberían ser semejantes (Ruiz et al., 2010).
Generalmente es preferible la utilización de diagramas para representar teorías que involucran muchas relaciones, dado que el uso de ecuaciones matemáticas puede dificultar la visualización del proceso causal involucrado. Para representar adecuadamente las ecuaciones mediante el uso de grafos se debe atender a ciertas convenciones:
- La relación causal entre variables se indica con una flecha cuyo sentido indica la dirección de la relación
- La covariación entre variables, sin interpretación direccional, se representa por medio de una flecha bidireccional
- Cada flecha presenta un coeficiente path que indica la magnitud del efecto entre ambas variables
- Las variables que reciben influencia por parte de otra se denominan endógenas y aquellas a las que no llega ninguna flecha exógena
- Las variables observables se enmarcan en cuadrados y las variables latentes en círculos.
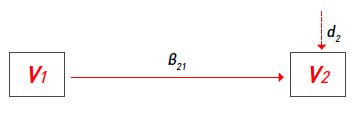
Por ejemplo, para representar un efecto causal de V1 en V2 se puede emplear una ecuación del tipo:
V2= β21 . V1+ d2
Donde d2 representa la perturbación aleatoria (disturbance) o variación de V2 por causas distintas a V1. Esta misma ecuación puede ser representada gráficamente en un diagrama path, de la siguiente manera:
Una vez elaborado el conjunto de ecuaciones o diagramas, se calcula para cada sendero un coeficiente similar al coeficiente de regresión que indica en qué medida los cambios de una variable se encuentran relacionados con los cambios en la otra variable (Aron & Aron, 2001). Hasta aquí el proceso se asemeja bastante a un análisis de regresión múltiple, sin embargo, los análisis basados en SEM poseen dos ventajas adicionales: (1) permite trabajar con variables latentes e incluye el error específico de medición del constructo, y (2) permite evaluar la concordancia de los datos estimados por el modelo con los datos observados mediante el uso de índices de ajuste, y de esta manera, pone a prueba el modelo causal postulado.
COMPONENTES DEL SEM: MODELO DE MEDIDA Y MODELO ESTRUCTURAL
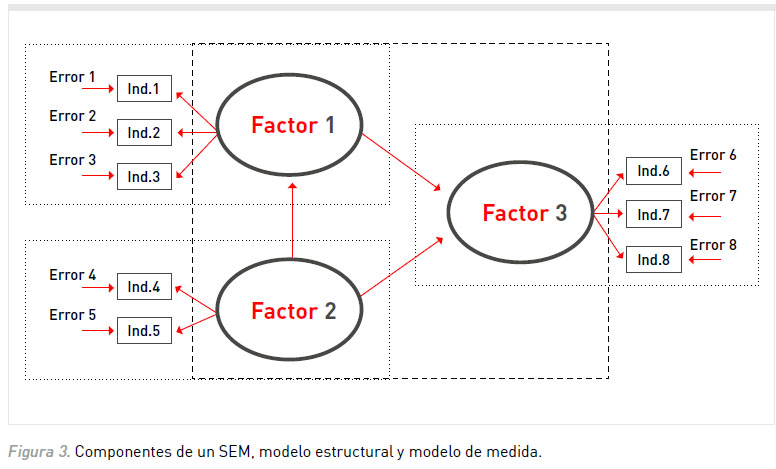
Es posible pensar al SEM como una combinación del análisis factorial y la regresión múltiple, lo que lleva a diferenciar dos componentes: el modelo de medida y el modelo estructural. En el modelo estructural se especifican las relaciones hipotetizadas entre las variables, es decir, se describen las relaciones entre las variables latentes mediante el uso de flechas. Por ejemplo, en el modelo ilustrado en la Figura 3 los factores 1 y 2 influyen directamente sobre el factor 3, y a su vez el factor 2 ejerce un efecto indirecto sobre el factor 3 a través del factor 1. Por otra parte, el modelo de medida describe la relación existente entre una serie de variables observables (por ejemplo, escalas de autoeficacia que miden el mismo constructo) y el constructo hipotéticamente medido (Byrne, 2001). Ambos componentes son diferenciados en la Figura 3, en el recuadro más grande se encierra al modelo estructural, mientras que en los recuadros más pequeños se señalan los modelos de medida.
De esta manera, la principal diferencia entre el SEM y la regresión múltiple radica en el modelo de medida, el cual evalúa qué tan bien las variables observables (o indicadores) se combinan para identificar el constructo subyacente hipotetizado. En este modelo se utiliza el análisis factorial confirmatorio para verificar si los indicadores seleccionados representan adecuadamente la variable latente de interés (Weston & Gore, 2006). La literatura recomienda utilizar al menos tres indicadores por factor, o en su defecto, llevar a cabo un path análisis (Batista-Foguet & Coenders, 2000).
Como se señaló con anterioridad, una segunda ventaja del SEM es la posibilidad de evaluar la concordancia de los datos estimados por el modelo con los datos observados mediante el uso de índices de ajuste, y de esta manera, poner a prueba el modelo causal postulado. Por ello el SEM es una técnica de gran utilidad para el desarrollo de modelos conceptuales, ya que permite poner a prueba modelos hipotéticos y mediante el contraste empírico adquirir nuevos insights teóricos que depuren el modelo inicialmente especificado. A su vez, el uso de teorías bien fundamentadas y sostenidas por la evidencia empírica favorecen una mejor aproximación a la realidad. De esta manera el SEM podría conceptualizarse como una técnica que mediatiza el proceso de ida y vuelta entre el desarrollo teórico y los hechos de la realidad (Blalock, 1964).
CINCO PASOS PARA LLEVAR A CABO UN SEM
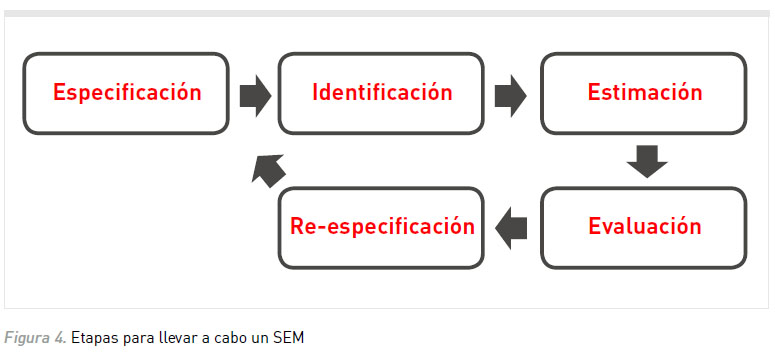
Llevar a cabo un SEM involucra básicamente cinco etapas (ver Figura 4):
1. Especificación del Modelo: En esta etapa el investigador establece cuáles serán las variables que se incluirán en el modelo explicativo y cuál es la relación que existe entre ellas. Esta primera etapa depende fundamentalmente del conocimiento teórico sobre el fenómeno por abordar. Un error frecuente en esta etapa es el de no incluir en el modelo variables relevantes o de importancia teórica, es por ello que antes de especificar un modelo debe efectuarse una revisión exhaustiva de la literatura. Por otra parte, la mera inclusión de variables sin un sustento teórico claro también constituye un error de especificación, ya que puede llevar a desarrollar modelos poco parsimoniosos y de bajo valor explicativo.
2. Identificación del Modelo: Antes de recolectar los datos se debe determinar si un modelo está correctamente identificado. Esta etapa consiste en examinar si se cuenta con la cantidad suficiente de información para contrastar el modelo. Cabe recordar que el SEM se basa en la estimación de covariaciones a partir de las relaciones causales que se especificaron en el modelo. Esto implica que cada parámetro por estimar debe ser derivable de la información contenida en la matriz de varianza-covarianza (Ruiz et al., 2010). Para determinar si el modelo está identificado los investigadores deben calcular los grados de libertad (gl), que se obtienen restando el número de parámetros a ser estimado, del número de elementos conocidos de la matriz de varianza-covarianza. Esto se logra mediante la siguiente fórmula:
gl= ½ x (Nº de variables observadas x (Nº de variables observadas + 1)) – Nº parámetros a estimar
Según los valores de gl obtenidos, el modelo puede clasificarse como subidentificado (gl < 0), identificado (gl = 0) o sobreidentificado (gl > 0). Solo aquellos modelos con menor cantidad de parámetros que varianzas y covarianza en la matriz observada (gl > 0) son susceptibles de ser estimados y contrastados. Además, la existencia de grados de libertad implica la parquedad o sencillez del modelo, en el sentido de que este explica la realidad a partir de un menor número de parámetros. Ello se debe a que los modelos con grados de libertad imponen restricciones en el espacio de las posibles matrices de covarianzas. Por el contrario, los modelos sin gl (sub-identificados o identificados) al no imponer estructura a la matriz de varianza/covarianza observada, se ajustan perfectamente a cualquier conjunto de datos y por tanto nunca pueden contrastarse.
3. Estimación del Modelo: La etapa de estimación consiste en obtener los valores de los parámetros especificados en el modelo a partir de las varianzas y covarianzas muestrales. Tal como se mencionó al inicio del artículo, con el SEM es posible estimar una covariación desde la descomposición de la covarianza, es decir que podría estimarse la covariación si se especifican correctamente los efectos causales que la provocan. El proceso de estimación consistiría en determinar cuáles serían los valores que deberían asumir los parámetros del modelo para obtener covariaciones que se asemejen a las covarianzas observadas en la muestra. Básicamente los diferentes métodos de estimación que se pueden utilizar comparten la misma lógica: obtener los valores de los parámetros (coeficientes de regresión o varianza de error, por ejemplo) que maximizan la igualdad entre las covarianzas pronosticadas por el modelo y las observadas en la muestra. Las diferencias entre los diferentes métodos de estimación radican fundamentalmente en la "función de ajuste" que utilizan, es decir, el método que utilizan para minimizar las diferencias con las covarianzas muestrales. El método más común de estimación es del de máxima probabilidad (ML, Maximum Likelihood) siempre que se cumplan los supuestos estadísticos, tales como disponer de una muestra de tamaño adecuado, medidas al menos de nivel intervalar, y distribución normal multivariada (Schermelleh-Engel, Moosbrugger, & Muller, 2003). No obstante, este método es robusto a ligeras desviaciones de la distribución normal (valores de hasta 70 en el coeficiente Mardia; Rodríguez Ayán & Ruiz, 2008). En caso de trabajar con datos ordinales o existir mayores alejamientos de la distribución normal se sugiere transformar los datos, utilizar métodos de bootstrapping o aplicar métodos de estimación alternativos como el Método de Estimación por Mínimos Cuadrados o el de Distribución Asintótica Libre (Flora & Curran, 2004), aunque este último requiere de tamaños muestrales superiores (de al menos 4000; Finch, West & MacKinnon, 1997) y no ha mostrado un buen funcionamiento (Hu, Bentler & Kano, 1992). Como regla general se recomienda utilizar ML (Iacobucci, 2010).
4. Evaluación del Modelo: La evaluación del ajuste tiene por objeto determinar si las relaciones entre las variables del modelo estimado reflejan adecuadamente las relaciones observadas en los datos (Weston & Gore, 2006). Esta aclaración es importante dado que en la regresión múltiple la idea de "ajuste" refiere a si el modelo estimado minimiza los errores de predicción cometidos (método de mínimos cuadrados). En SEM en vez de evaluar la diferencia entre los valores pronosticados y los observados, se evalúa la diferencia entre las covarianzas observadas en la muestra y las pronosticadas por el modelo especificado (Ruiz et al., 2010). Existen tres tipos de estadísticos de bondad de ajuste: (a) los de ajuste absoluto (chi cuadrado, por ejemplo), que no utilizan un modelo alternativo para contrastar sino que directamente analizan el ajuste entre la matriz de covarianza observada y la reproducida por el método de estimación; (b) los de ajuste relativo que comparan el ajuste respecto de otro modelo (CFI, por ejemplo) y, (c) los de ajuste parsimonioso (NFI, por ejemplo), que valoran el ajuste con respecto al número de parámetros utilizados. Ninguno de estos estadísticos de ajuste aporta toda la información necesaria para valorar el modelo, por lo cual se recomienda utilizar múltiples indicadores de ajuste. En una revisión realizada por Jackson et al. (2009), se observó que los índices más utilizados en la literatura especializada eran el índice de ajuste comparado (CFI), el índice de ajuste no normado (TLI), la raíz cuadrada media del error de aproximación (RMSEA) y el índice de bondad del ajuste (GFI).
Los valores críticos utilizados para evaluar el ajuste de un modelo han ido variando a lo largo del tiempo. Por ejemplo, para el índice CFI, Bentler y Bonett (1980) recomendaron un punto de corte de .90, posteriormente Hu y Bentler (1999) elevaron dicho valor a .95, e incluso algunos autores sugirieron un punto de corte de .97 (Schermelleh-Engel et al., 2003). Probablemente los puntos de corte más utilizados para evaluar los índices de ajustes sean los propuestos por Hu y Bentler (1999), considerados por muchos investigadores como la "biblia" de los puntos de corte (Barrett, 2007). Dichos autores recomiendan valores superiores a .95 para los índices CFI, TLI y GFI para considerar un ajuste óptimo, y superiores a .90 para un ajuste aceptable. Por otra parte, valores inferiores a .06 para el RMSEA se consideran óptimos e inferiores a .08 aceptables. Sin embargo, algunos investigadores han criticado la adopción de límites tan estrictos (Barrett, 2007; Marsh, Hau & Wen, 2004; Yuan, 2005), y otros han planteado una postura intermedia, reconociendo la utilidad de dichos puntos de corte, pero recomendando su utilización con cautela o bien contemplando el tamaño muestral involucrado (Bentler, 2007; Miles & Shevlin, 2007; Sivo, Fan, Witta & Willse, 2006).
Chi cuadrado (χ²) es una medida fundamental para valorar el ajuste global del modelo, y es el único índice que posee una prueba de significación estadística asociada. En caso de no obtener resultados estadísticamente significativos (valores p superiores a 0.05) se acepta la hipótesis nula de igualdad entre las matrices de covarianza observada y reproducida. Sin embargo, este índice tiene algunas dificultades. En primer lugar, los valores de χ² tienden a disminuir en la medida en que se suman parámetros al modelo. Los valores de χ² tenderán a ser inferiores en modelos más complejos que en modelos simples por la reducción de grados de libertad (Hooper, Couglan & Mullen, 2008). En segundo lugar, cuando el tamaño muestral es mayor y manteniendo constantes los grados de libertad, los valores de χ² tienden a aumentar. Esto implica que cuanto mayor sea el tamaño de la muestra peor será el ajuste. Es decir que incluso leves diferencias entre las matrices generarán resultados estadísticamente significativos (p<.05). Por ello no se recomienda utilizar χ² como prueba estadística, sino simplemente como una medida descriptiva de ajuste. Una versión alternativa que permite ponderar el tamaño muestral es la división del coeficiente χ² por los grados de libertad (χ²/gl). De acuerdo con la literatura, valores inferiores a 3 indican un buen ajuste (Iacobucci, 2010; Kline, 2005).
Por otra parte, el coeficiente χ² resulta especialmente útil cuando deben compararse modelos rivales. De esta manera, si estamos en presencia de dos modelos teóricos que presentan un ajuste aceptable, debemos inclinarnos por el que posea menores valores de χ². Además del χ² es habitual que se recurra a índices o criterios alternativos como el Criterio de Información de Akaike (AIC). Este índice ajusta el estadístico chi-cuadrado al número de grados de libertad del modelo. Valores inferiores de AIC para un modelo indican su relativo mejor ajuste respecto de los modelos alternativos.
Finalmente resta por señalar que la evaluación de un modelo no se restringe al examen de los índices de ajuste, sino que deben analizarse también la magnitud de los parámetros estimados y la varianza explicada por las variables.
5. Re-especificación del Modelo: El análisis del ajuste del modelo no acaba con el examen de los índices de ajuste. Un análisis pormenorizado de los residuos permite detectar problemas inadvertidos en el diagnóstico global, y sugerir posibles modificaciones del modelo para mejoralo. De esta manera, residuos elevados entre parejas de variables implican la necesidad de introducir parámetros adicionales susceptibles de explicar la relación entre las variables en cuestión. A partir de la inspección de dichos residuos es posible efectuar re-especificaciones en el modelo para mejorar su ajuste. Es importante que las decisiones de añadir o eliminar parámetros sean coherentes con la teoría subyacente al modelo.
Una inspección de los índices de modificación suele resultar de mucha utilidad en esta etapa. El valor del índice de modificación corresponde aproximadamente a la reducción en el c² que se produciría si el coeficiente fuera estimado. Un valor > 3.84 sugiere que se obtiene una reducción estadísticamente significativa en el c² cuando se estima el coeficiente. Es importante no efectuar re-especificaciones que no pueden sustentarse a nivel teórico. De lo contrario se derivará en un modelo ajustado a la muestra en estudio, pero de pobre fundamento teórico.
Si bien los análisis mediante SEM pueden sintetizarse grosso modo en estas cinco etapas, conviene tener en consideración algunos aspectos adicionales. Un aspecto de importancia es el tamaño muestral. Según Barrett (2007) el tamaño muestral no puede ser inferior a 200 e incluso otros autores sugieren valores superiores a 400 cuando se utiliza máxima probabilidad como método de estimación (Boomsma & Hoogland, 2001; Schermelleh-Engel et al., 2003). Sin embargo, también se plantea la posibilidad de alcanzar un buen ajuste a pesar de tener un tamaño muestral inferior a 200 (Hayduk et al., 2007; Markland, 2007). Si bien un tamaño muestral grande es deseable, ya que aumenta la potencia de las pruebas, debe reconocerse que hay otros factores que pueden afectar la potencia, como por ejemplo poseer pequeños errores de medición o trabajar con variables observables que tengan pequeñas varianzas únicas y mayor varianza compartida (Browne, MacCallum, Kim, Andersen & Glaser, 2002). Como regla general puede decirse que poseer muestras grandes siempre es mejor, pero si el modelo es simple, cuenta con mediciones limpias (ítems con elevadas cargas factoriales y factores confiables), y posee efectos fuertes, pueden utilizarse muestras más pequeñas (Bollen, 1990; Iacobucci, 2010).
Otro aspecto para considerar es el de trabajar con variables que no presenten una distribución normal. Como se mencionó con anterioridad, en el contexto del SEM es habitual la asunción del supuesto de normalidad multivariada. Es importante recordar que la distribución de muestreo de un estadístico es clave cada vez que se efectúe un proceso de inferencia estadística. Por ejemplo, para estimar un intervalo de confianza debemos conocer el parámetro (se puede obtener a partir de los datos muestrales) y disponer de una estimación del error típico (la cual depende de la distribución de muestreo en cuestión). Algunos procedimientos estadísticos efectúan inferencias asumiendo que los datos se distribuyen normalmente. Por ejemplo, el test de Sobel, utilizado para evaluar la significación estadística de los efectos indirectos, asume normalidad. Esto quiere decir que el incumplimiento de dicho supuesto puede mermar el control del error tipo 1 (Preacher & Hayes, 2008).
En este escenario han cobrado popularidad los métodos de re-muestreo de datos, entre los que se encuentran el Jacknife y el bootstrap. La lógica subyacente de esos métodos es la de extraer un gran número de muestras repetidas con reposición a partir de los datos observados (Ledesma, 2008). La ventaja de estos procedimientos es que permite estimar estas propiedades aproximando empíricamente la distribución de muestreo del estadístico en cuestión, es decir sin los supuestos habituales de normalidad (Enders, 2005). En términos simples, el bootstrap consiste en crear un gran número de submuestras con reposición de los mismos datos (mil muestras, por ejemplo) y, posteriormente, calcular para cada muestra resultante el valor del estadístico en cuestión. Se obtiene así una aproximación a la distribución de muestreo del estadístico, a partir de la cual podemos realizar inferencias (por ejemplo, construir un intervalo de confianza). De esta manera es posible prescindir de supuestos relativos a las distribuciones, ya que en vez de asumir a priori una determinada distribución teórica el bootstrap genera una distribución empírica a partir del re- muestreo. De esta manera se puede examinar la estabilidad de los parámetros estimados y reportar estos valores con mayor nivel de precisión (Byrne, 2001). Esta metodología ha demostrado ser eficiente en una gran variedad de situaciones (como por ejemplo análisis de correlación y regresión), y en particular en análisis basados en SEM (Fan, 2003). En la siguiente sección se ilustrarán las cinco etapas descritas para realizar un SEM, así como la utilización del bootstrap mediante el programa AMOS.
LOS 5 PASOS DEL SEM UTILIZANDO EL PROGRAMA AMOS
Los análisis basados en SEM pueden llevarse a cabo con diferentes programas. En 1973, Jöreskog desarrolló el programa LISREL (Linear Structural Relations), siendo este el primer software que permitía realizar SEM (Ruiz et al., 2010). Otro programa utilizado tradicionalmente es el EQS (abreviatura de Equations), desarrollado por Bentler (1985). Ambos programas son muy utilizados, pero requieren el uso de sintaxis, lo cual puede resultar problemático para usuarios noveles. Como alternativa Arbuckle (1997) desarrolló el AMOS (Analysis of Moment Structures) el cual posee un entorno gráfico que resulta más amigable, aunque también permite especificar modelos utilizando sintaxis. A continuación, se ejemplifica el uso de SEM en 5 pasos utilizando la interfaz gráfica de AMOS.
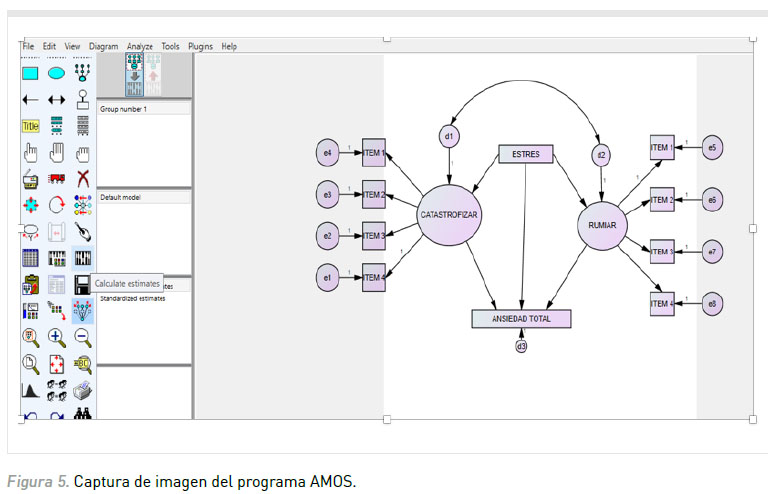
Para ilustrar el uso de AMOS se utilizará el ejemplo de una investigación en que se evaluó si el estrés percibido y los procesos cognitivos de rumiación y catastrofización, predecían los niveles de ansiedad de una persona. Desde este modelo se plantea que frente a una situación de estrés se inician de manera automática procesos cognitivos de rumiación (tendencia a perseverar en pensamientos negativos y preocupaciones excesivas) y catastrofización (tendencia a exagerar o ampliar las consecuencias negativas de un evento) que aumentan los niveles de ansiedad y los perpetúan (Medrano, Muñoz & Cano-Vindel, 2016). Luego de administrar una serie de instrumentos a una muestra de 386 participantes se procede a realizar los análisis con SEM utilizando AMOS 20.
1. Estimación del modelo con AMOS: La especificación de modelos con el programa AMOS es más simple que en otros programas (como por ejemplo LISREL). Esto se debe a que AMOS permite utilizar una interfaz gráfica para especificar las relaciones hipotetizadas entre las variables en cuestión. Para ello simplemente debe representarse el modelo utilizando las herramientas que figuran en el tablero del programa. Es importante representar adecuadamente las ecuaciones atendiendo a las convenciones sobre el uso de los grafos, las cuales fueron expuestas al inicio del artículo (ver Figura 5).
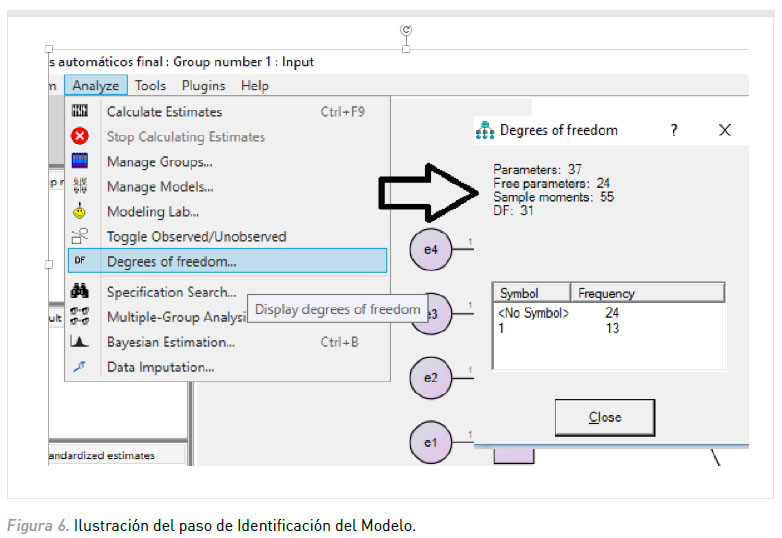
2. Identificación del modelo con AMOS: Para verificar si el modelo posee la cantidad suficiente de grados de libertad para ser estimado y contrastado es suficiente con efectuar un click sobre el menú Analyze/Degree of freedoms. Inmediatamente se podrá visualizar una ventana que informa la cantidad de grados de libertad del modelo. En este caso el modelo cuenta con 31 grados de libertad (ver Figura 6).
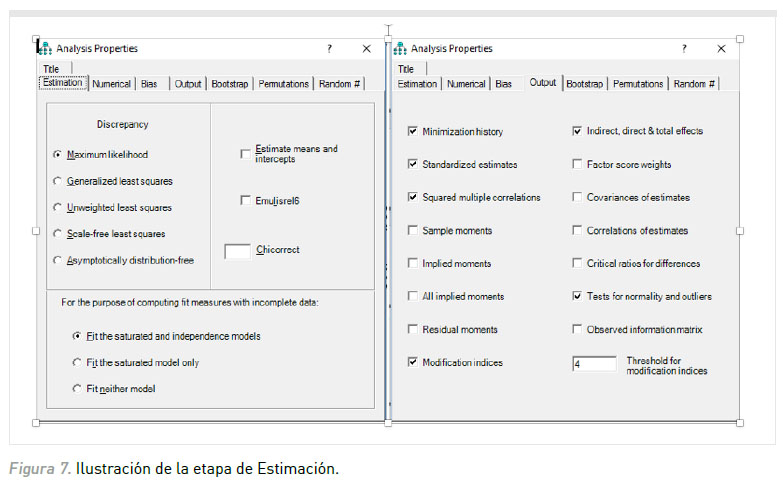
3. Estimación del modelo con AMOS: El programa AMOS presenta por defecto el método de máxima probabilidad; no obstante, en caso de que deseemos utilizar otro método el mismo puede seleccionarse efectuando un click sobre el icono Analysis properties, y posteriormente elegir el método de estimación que se considere más apropiado. Una vez seleccionado el método se debe solicitar al programa que efectúe la estimación del modelo haciendo click sobre Analyze/Calculates Estimates (ver Figura 7). En este ejemplo se utilizó el método de estimación por máxima probabilidad. En el mismo cuadro de diálogo puede seleccionarse en Output, la información que desea obtenerse. En el caso del ejemplo (ver Figura 7) se solicitó al programa los coeficientes de regresión estandarizados, los coeficientes de determinación (R²), los efectos indirectos, directos y totales, los índices de modificación e información relativa a la normalidad multivariada y casos atípicos.
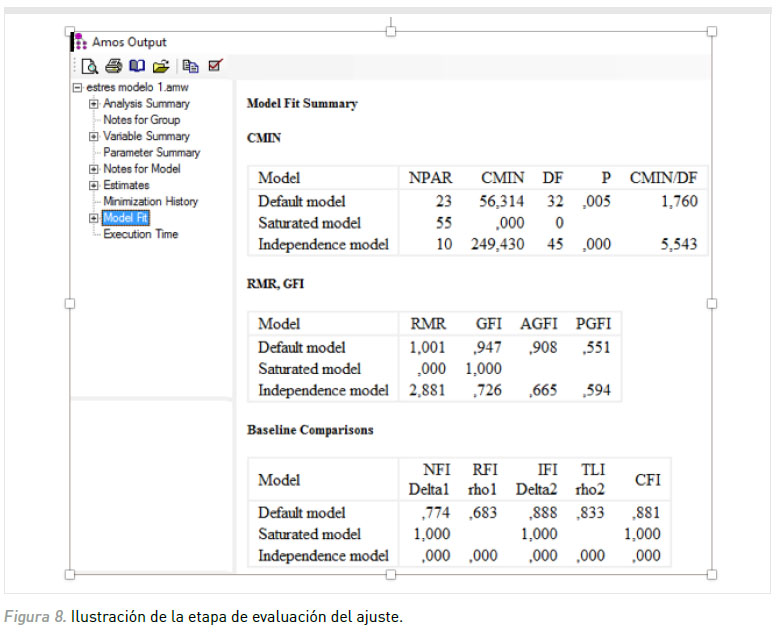
4. Evaluación del modelo con AMOS: Para evaluar el ajuste del modelo debe efectuarse un click sobre "Model Fit" e inspeccionar los valores obtenidos en los índices de ajuste (ver Figura 8). Algunos de los índices de ajuste obtenidos en este modelo fueron: CFI=.88; GFI=.95; RMSEA=.06. También deben examinarse los coeficientes de regresión estandarizados para corroborar los relaciones hipotetizadas en el modelo.
5. Re-especificación del modelo con AMOS: En esta etapa es útil inspeccionar los índices de modificación. Esta información debe ser solicitada dado que AMOS no la incluye por defecto. Para ello se debe seleccionar el ícono de Analysis Properties, y clickear sobre la solapa "Outpout". Allí el usuario puede seleccionar la visualización de información adicional. En este caso debe seleccionarse: "Modification indices". Tal como se explicó esta información es provechosa para generar modificaciones en el modelo, sin embargo es muy importante s precaver y no incluir parámetros sin un sustento teórico claro. De lo contrario el modelo comienza a perder valor teórico.
Como se mencionó anteriormente, trabajar con distribuciones no normales puede afectar notablemente los análisis mediante SEM, sobre todo cuando se utiliza máxima verosimilitud, ya que este método de estimación se basa en el supuesto de normalidad multivariada. Aunque este método es robusto al incumplimiento de la normalidad (funciona adecuadamente incluso con valores de Mardia de 70, Rodríguez Ayán & Ruiz, 2008), se recomienda complementar los análisis con Bootstrap cuando el alejamiento de la normalidad es mayor. Para ello, dentro del cuadro de diálogo de la Figura 7 debe seleccionarse la opción Boostrap, Posteriormente se debe especificar la cantidad de muestras que se utilizarán para el re-muestreo y el intervalo de confianza deseado. La literatura recomienda utilizar entre 500 y 1000 replicaciones de bootstrap (Cheung & Lau, 2008) y utilizar intervalos de confianza corregidos al 90% (Bias-correted confidence intervals). Otra opción disponible es la de utilizar la aproximación Bollen-Stine para evaluar el ajuste absoluto del modelo. Esta aproximación sirve como alternativa al tradicional χ² y su interpretación es simple, ya que se considera que el modelo posee un ajuste aceptable si los valores p obtenidos son superiores a.05. Sin embargo, aunque es un complemento interesante, la opción Bollen-Stine es altamente sensible por lo que se obtendrán valores p significativos incluso frente a leves diferencias entre las matrices (Byrne, 2001). Es por esto que también deben analizarse múltiples índices de ajuste cuando se utiliza la metodología bootstrap.
BUENAS PRÁCTICAS EN EL REPORTE DE SEM
Un aspecto importante de las buenas prácticas en la utilización de SEM se refiere a la información que debe reportarse cuando se publican trabajos que utilicen esta metodología. Las buenas prácticas en el reporte de información son claves para el progreso de la ciencia. En efecto, se debe proveer toda la información necesaria para que el lector pueda comprender las decisiones tomadas por los investigadores y analizar la robustez de los resultados. Reportar adecuadamente es aún más importante cuando dos estudios arriban a conclusiones diferentes sobre el mismo tema. En estos casos es de especial importancia evaluar si las diferencias observadas no son atribuibles a aspectos metodológicos.
Aunque no hay criterios universales respecto a cómo se debe reportar la información en un estudio SEM, existe un acuerdo generalizado con relación a los siguientes puntos (Jackson et al., 2009):
1. Fundamentos teóricos y recolección de datos: los autores deben justificar con claridad todos los parámetros que se especificaron en el modelo. Antes de reportar los resultados se debe presentar argumentos teóricos sólidos que expliquen el modelo formulado, y de ser posible, presentar también modelos rivales que puedan resultar de interés. Asimismo, se debe justificar la elección de los instrumentos utilizados y la adecuación del tamaño muestral.
2. Preparación de los datos: debe reportarse el examen de los supuestos estadísticos, como por ejemplo la normalidad multivariada. Otro aspecto para señalar es el tratamiento de los valores perdidos, por ejemplo, explicando si se ha utilizado un método de imputación de datos o se ha optado por la estrategia de listwise deletion, la cual suele ser la más utilizada (McKnight, McKnight, Sidani, & Figueredo, 2007). También se recomienda especificar los criterios para la detección y tratamiento de los casos atípicos, indicar si se ha utilizado algún método de transformación en caso de incumplimiento de la normalidad, y los criterios para el parcelamiento de ítems en caso de que se utilice dicha metodología (para una discusión más profunda de este punto ver Little, Cunningham, Shahar & Widaman, 2002)
3. Decisiones con relación a los análisis: una vez preparados los datos, los investigadores se enfrentan a dos decisiones importantes: ¿qué matriz de datos y qué método de estimación utilizar? La mayor parte de las investigaciones utilizan la matriz de varianza-covarianza y el método de estimación de máxima probabilidad, pero, aun así, siempre es importante explicitar ambos aspectos. Por otra parte, en algunos casos puede resultar más ventajoso utilizar una opción alternativa. Por ejemplo, utilizar el método de mínimos cuadrados en caso de incumplimiento o un abordaje basado en el re-muestreo de datos, sobre todo si se trabaja con muestras pequeñas o no se cumple el supuesto de normalidad. También es importante indicar cuál fue el software que se usó para realizar los análisis.
4. Evaluación y modificación del modelo: se debe explicitar los criterios para determinar los puntos de corte y la selección de los índices de ajustes. Además de reportar los índices de ajustes se sugiere analizar los residuos estandarizados para evaluar con mayor precisión el funcionamiento de los parámetros especificados. Las re-especificaciones en el modelo no deben efectuarse solamente por la consideración de los índices de modificación. Debe explicitarse con claridad las razones teóricas que justifican la inclusión de nuevos parámetros o modificaciones con respecto al modelo original.
5. Reporte de hallazgos: los análisis basados en SEM generan un gran volumen de información, por lo cual se recomienda discernir con cuidado al decidir qué información comunicar. Se debe evitar la inclusión de resultados estadísticos innecesarios o que presenten poca contribución en la comprensión del trabajo. Más concretamente, se recomienda reportar los parámetros de estimación (saturaciones factorial y coeficientes path estandarizados), varianza de las variables exógenas y la proporción de varianza explicada de las variables endógenas. En caso de contrastar modelos rivales se debe comunicar con claridad cuál es el modelo elegido por el autor y fundamentar su decisión no solo por el ajuste del modelo, sino por sus implicancias teóricas.
CONCLUSIONES
Los análisis basados en SEM constituyen en la actualidad la estrategia de análisis preferida por los investigadores para datos no experimentales. Sin embargo, son pocos los trabajos en castellano que brinden una aproximación a los mismos centrada en aspectos conceptuales y lógicos, permitiendo al lector no especializado introducirse en el análisis SEM.
En este artículo metodológico se examinaron los fundamentos conceptuales y lógicos de los modelos de ecuaciones estructurales, y se ilustró su utilización con el programa AMOS. Es importante señalar que este artículo posee un carácter introductorio y no reemplaza literatura más profunda sobre el tema, sin embargo, se espera que sea un trabajo de interés y relevancia para el lector no especializado. El mismo brinda un marco adecuado suficiente para orientar el proceso de toma de decisiones involucrado en el SEM. De esta manera se espera contribuir al desarrollo de investigaciones que utilicen esta metodología en el ámbito latinoamericano.
El SEM constituye una técnica de gran utilidad para el desarrollo de modelos conceptuales, ya que permite poner a prueba modelos hipotéticos y mediante el contraste empírico adquirir nuevos insights teóricos que depuren el modelo inicialmente especificado. De esta manera, el SEM podría conceptualizarse como una técnica que mediatiza el proceso de ida y vuelta entre el desarrollo teórico y los hechos de la realidad (Blalock, 1964).
Para muchos los SEM constituyen la metodología más potente cuando se trabaja con datos no experimentales (Aron & Aron, 2001), sin embargo debe destacarse que la potencia y utilidad de esta metodología depende fundamentalmente de contar con un adecuado modelo teórico de base. Lamentablemente se observa con frecuencia un uso inadecuado de este procedimiento, consistente en incluir o quitar parámetros en función de la mejora del ajuste del modelo. Esta modalidad de trabajo con SEM se encuentra fuertemente discutida, ya que la solidez del modelo no provendrá solo del ajuste estadístico del mismo, sino de su coherencia teórica.
Al respecto cabe señalar algunas sugerencias que permitirán un examen juicioso de los modelos obtenidos a partir de SEM. Al respecto cabe considerar los criterios comunicados por Hawking y Mlodino (2010) para analizar si un modelo resulta satisfactorio:
- 1) es elegante,
- 2) contiene pocos elementos arbitrarios o ajustables,
- 3) concuerda con las observaciones existentes y proporciona una explicación de ellas
- 4) realiza predicciones detalladas que permitirán refutar o falsear el modelo.
La elegancia de un modelo no es algo que se pueda evaluar fácilmente, pero es muy apreciada entre los científicos dado que implica la ausencia de elementos ajustables o explicaciones "pos facto". Un ejemplo de falta de elegancia sería incluir correlaciones nuevas o quitar ítems, o correlacionar errores solamente para mejorar el ajuste del modelo. Este tipo de "correcciones" llevan a forzar al modelo para que se ajuste a un conjunto específicos de observaciones, generándose un modelo "a medida" más que a una teoría útil.
Generalmente la ausencia de elegancia proviene de los intentos tenaces por rescatar un modelo que no presenta un buen ajuste. Cabe señalar que es lícito introducir cambios que permitan mejorar el ajuste o valor predictivo del modelo, pero sólo si éstos se encuentran teóricamente fundamentados. Por el contrario, generar alteraciones artificiosas y poco argumentadas lleva a que el modelo se torne ininteligible. Estos modelos "sobre-manipulados" suelen ser muy inestables y pierden su buen ajuste cuando se replican en otra muestra. Esto sucede porque los índices de modificación solo indican que nuevos parámetros pueden mejorar el ajuste del modelo a la matriz de covarianza de la muestra en estudio, pero lógicamente dichos parámetros pueden resultar poco beneficiosos en otra muestra. Por ello es recomendable re-especificar parámetros solo cuando existe sustento teórico y no guiarse únicamente por los índices de modificación. De lo contrario se obtendrán modelos con mucho ajuste para muestras particulares y con poco poder de generalización.
Con relación a este tema cabe destacar las críticas de Hayduk et al. (2007) al énfasis que algunos autores otorgan al ajuste de los SEM (Barrett, 2007). El objetivo del SEM no es obtener modelos que ajusten bien, sino el de contrastar teorizaciones. Debe reconocerse que en la literatura científica pueden encontrarse muchos trabajos que se centran más en el ajuste que en el modelo teórico que provee dicho ajuste. Lamentablemente es una práctica habitual entre los investigadores centrarse en el análisis superficial de los valores estadísticos, y perder de vista cuestiones teóricas sustantivas. Como señala Hayduk et al. (2007) "abandonar del razonamiento teórico, es abandonar la esencia misma de la ciencia" (p. 842).
Además de la elegancia, la existencia de pocos elementos arbitrarios y el ajuste del modelo a los datos, es importante considerar el poder predictivo del modelo. Contar con predicciones acertadas implica que el modelo se encuentra correctamente formulado, aumentando la solidez del mismo. Otro aspectodestacable es el planteado por Barrett (2007), quien sugiere que muchos modelos SEM no presentan variables observables ancladas "en el mundo real". La ausencia de un criterio externo puede llevar a que muchos modelos SEM sean simplemente un modelo estadístico que explique la co-variación entre diferentes constructos teóricos. En efecto, muchos investigadores construyen modelos "ciegos" o "mecánicos" donde se "crean" una o varias variables latentes para explicar las variaciones causales, sin un criterio externo que permita contrastar dicho modelo.
También es importante destacar que, aunque un modelo presente un buen ajuste, esto no descarta que puedan existir otros modelos que también tengan la misma característica, simplemente indica que es uno de los modelos que potencialmente pueden presentar un buen ajuste a los datos. Por ello es recomendable contrastar diferentes modelos que también puedan estar avalados por la teoría o incluso sustentados en una teoría rival (Hayduk et al., 2007). En función de ello es recomendable evaluar el ajuste de diferentes modelos, con el fin de analizar si otros son igualmente plausibles.
Otro aspecto controvertido proviene de la afirmación de Barrett (2007, p.820) "si el modelo ajusta el investigador procederá a informar y discutir las características del modelo". Frente a ello surge el siguiente interrogante: ¿Los investigadores no deberían también publicar y discutir sobre los modelos que no presentan un buen ajuste? En este sentido, Hayduk et al. (2007) sostienen que la discusión sobre los modelos que no ajustan adecuadamente es crucial para el desarrollo científico de una disciplina, ya que no reconocer abiertamente las deficiencias de los modelos teóricos que se están utilizando puede obstaculizar el paso a teóricas más adecuadas.
En la ciencia psicológica contemporánea se observan numerosos modelos SEM que cumplen con los requerimientos mencionados. Esto permite a científicos y profesionales contar con modelos teóricos sólidos que brinden mayores garantías y sustento en el proceso de toma de decisiones.
REFERENCIAS
Arbuckle, J. L. (1997). Amos Users’ Guide. Version 3.6 . Chicago: SmallWaters Corporation.
Aron, A. & Aron, E. (2001) Estadística para Psicología. Buenos Aires: Pearson Education. [ Links ]
Bagozzi, R. P., & Yi, Y. (2012). Specification, evaluation, and interpretation of structural equation models. Journal of the academy of marketing science, 40(1), 8-34. doi: http://dx.doi.org/10.1007/s11747-011-0278-x [ Links ]
Barrett, P. (2007). Structural equation modelling: Adjudging model fit. Personality and Individual differences, 42(5), 815-824. doi: http://dx.doi.org/10.1016/j.paid.2006.09.018 [ Links ]
Batista-Foguet, J. M. & Coenders, G. (2000). Modelos de Ecuaciones Estructurales. Madrid: La Muralla, S.A. [ Links ]
Bentler, P. M. (1985). Theory and implementation of EQS: A structural equations program. Los Angeles: BMDP Statistical Software [ Links ]
Bentler, P. M. (2007). On tests and indices for evaluating structural models. Personality and Individual Differences, 42(5), 825-829. doi: http://dx.doi.org/10.1016/j.paid.2006.09.024 [ Links ]
Bentler, P. M., & Bonett, D. G. (1980). Significance tests and goodness of fit in the analysis of covariance structures. Psychological bulletin, 88(3), 588-606. doi: http://dx.doi.org/10.1037/0033-2909.88.3.588 [ Links ]
Blalock, H. M., Jr. (1964). Causal inferences in non-experimenta research. Chapel Hill: University of North Carolina Press. [ Links ]
Bollen, K. A. (1990). Overall fit in covariance structure models: two types of sample size effects. Psychological bulletin, 107(2), 256-259. [ Links ]
Boomsma, A., & Hoogland, J. J. (2001). The robustness of LISREL modeling revisited. Structural equation models: Present and future. A Festschrift in honor of Karl Jöreskog, 139-168.
Browne, M. W., MacCallum, R. C., Kim, C. T., Andersen, B. L., & Glaser, R. (2002). When fit indices and residuals are incompatible. Psychological methods, 7(4), 403-421. doi: https://doi.org/10.1037//1082-989X.7.4.403 [ Links ]
Byrne, B. M. (2001). Structural equation modeling with AMOS: Basic concepts, applications, and programming. Mahwah, NJ: Lawrence Erlbaum. [ Links ]
Cheung, G. W., & Lau, R. S. (2008). Testing mediation and suppression effects of latent variables: Bootstrapping with structural equation models. Organizational Research Methods, 11(2), 296-325. doi: https://doi.org/10.1177/1094428107300343 [ Links ]
DiStefano, C., & Hess, B. (2005). Using confirmatory factor analysis for construct validation: An empirical review. Journal of Psychoeducational Assessment, 23(3), 225-241. doi: https://doi.org/10.1177/073428290502300303 [ Links ]
Enders, C. K. (2005). An SAS macro for implementing the modified Bollen-Stine bootstrap for missing data: Implementing the bootstrap using existing structural equation modeling software. Structural Equation Modeling, 12(4), 620-641. [ Links ]
Fan, X. (2003). Using commonly available software for bootstrapping in both substantive and measurement analyses. Educational and Psychological Measurement, 63(1), 24-50. doi: https://doi.org/10.1177/0013164402239315 [ Links ]
Finch, J. F., West, S. G., & MacKinnon, D. P. (1997). Effects of sample size and nonnormality on the estimation of mediated effects in latent variable models. Structural Equation Modeling: A Multidisciplinary Journal, 4(2), 87-107. doi: http://dx.doi.org/10.1080/10705519709540063 [ Links ]
Flora, D. B., & Curran, P. J. (2004). An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychological methods, 9(4), 466. doi: https://doi.org/10.1037/1082-989X.9.4.466 [ Links ]
Hawking S. W. &Mlodino L. (2010). The Grand Desing. New York: Bantam Books. [ Links ]
Hayduk, L., Cummings, G., Boadu, K., Pazderka-Robinson, H., & Boulianne, S. (2007). Testing! testing! one, two, three–Testing the theory in structural equation models!. Personality and Individual Differences, 42(5), 841-850. doi: http://dx.doi.org/10.1016/j.paid.2006.10.001 [ Links ]
Hooper, D., Coughlan, J. and Mullen, M. R. (2008). Structural Equation Modelling: Guidelines for Determining Model Fit. The Electronic Journal of Business Research Methods, 6(1), 53–60. [ Links ]
Hu, L. T., & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural equation modeling: a multidisciplinary journal, 6(1), 1-55. doi: http://dx.doi.org/10.1080/10705519909540118 [ Links ]
Hu, L. T., Bentler, P. M., & Kano, Y. (1992). Can test statistics in covariance structure analysis be trusted? Psychological bulletin, 112(2), 351. doi: http://dx.doi.org/10.1037/0033-2909.112.2.351 [ Links ]
Iacobucci, D. (2009). Everything you always wanted to know about SEM (structural equations modeling) but were afraid to ask. Journal of Consumer Psychology, 19(4), 673-680. doi: http://dx.doi.org/10.1016/j.jcps.2009.09.002 [ Links ]
Iacobucci, D. (2010). Structural equations modeling: Fit indices, sample size, and advanced topics. Journal of Consumer Psychology, 20(1), 90-98. doi: http://dx.doi.org/10.1016/j.jcps.2009.09.003 [ Links ]
Jackson, D. L., Gillaspy Jr, J. A., & Purc-Stephenson, R. (2009). Reporting practices in confirmatory factor analysis: an overview and some recommendations. Psychological methods, 14(1), 6-23. doi: http://dx.doi.org/10.1037/a0014694 [ Links ]
Kline, R. B. (2005). Principles and practice of structural equation modeling (2nd ed.). New York: Guilford [ Links ]
Ledesma, R. (2008). Introduccción al Bootstrap. Desarrollo de un ejemplo acompañado de software de aplicación. Tutorials in Quantitative Methods for Psychology, 4(2), 51-60. [ Links ]
León, O. G. & Montero I. (2003). Métodos de Investigación en Psicología y Educación (3ra edición). España: Mc Graw Hill. [ Links ]
Little, T. D., Cunningham, W. A., Shahar, G., & Widaman, K. F. (2002). To parcel or not to parcel: Exploring the question, weighing the merits. Structural equation modeling, 9(2), 151-173. [ Links ]
MacCallum, R. C., & Austin, J. T. (2000). Applications of structural equation modeling in psychological research. Annual review of psychology, 51(1), 201-226. doi: http://dx.doi.org/10.1146/annurev.psych.51.1.201 [ Links ]
Markland, D. (2007). The golden rule is that there are no golden rules: A commentary on Paul Barrett’s recommendations for reporting model fit in structural equation modelling. Personality and Individual Differences, 42(5), 851-858. doi: http://dx.doi.org/10.1016/j.paid.2006.09.023
Marsh, H. W., Hau, K. T., & Wen, Z. (2004). In search of golden rules: Comment on hypothesis-testing approaches to setting cutoff values for fit indexes and dangers in overgeneralizing Hu and Bentler’s (1999) findings. Structural equation modeling, 11(3), 320-341. doi: http://dx.doi.org/10.1207/s15328007sem1103_2
Martens, M. P., & Haase, R. F. (2006). Advanced applications of structural equation modeling in counseling psychology research. The Counseling Psychologist, 34(6), 878-911. doi: https://doi.org/10.1177/0011000005283395 [ Links ]
McKnight, P. E., McKnight, K. M., Sidani, S., & Figueredo, A. J. (2007). Missing data: A gentle introduction. Guilford Press. [ Links ]
Medrano, L. A., Muñoz-Navarro, R., & Cano-Vindel, A. (2016). Procesos cognitivos y regulación emocional: aportes desde una aproximación psicoevolucionista. Ansiedad y Estrés, 22(2-3), 47-54. doi: http://dx.doi.org/10.1016/j.anyes.2016.11.001 [ Links ]
Miles, J., & Shevlin, M. (2007). A time and a place for incremental fit indices. Personality and Individual Differences, 42(5), 869-874. doi: http://dx.doi.org/10.1016/j.paid.2006.09.022 [ Links ]
Preacher, K. J., & Hayes, A. F. (2008). Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models. Behavior research methods, 40(3), 879-891. doi: http://dx.doi.org/10.3758/BRM.40.3.879 [ Links ]
Rodríguez Ayán, M. y Ruiz, M. (2008). Atenuación de la asimetría y de la curtosis de las puntuaciones observadas mediante transformaciones de variables: Incidencia sobre la estructura factorial. Psicológica, 29, 205-227 [ Links ]
Ruiz, M. A.; Pardo, A. & San Martin, R. (2010). Modelos de ecuaciones estructurales. Papeles del psicólogo, 31(1), 34-45. [ Links ]
Schermelleh-Engel, K., Moosbrugger, H., & Müller, H. (2003). Evaluating the fit of structural equation models: Tests of significance and descriptive goodness-of-fit measures. Methods of psychological research online, 8(2), 23-74. [ Links ]
Sivo, S. A., Fan, X., Witta, E. L., & Willse, J. T. (2006). The search for" optimal" cutoff properties: Fit index criteria in structural equation modeling. The Journal of Experimental Education, 74(3), 267-288. doi: http://dx.doi.org/10.3200/JEXE.74.3.267-288 [ Links ]
Weston, R. & Gore Jr., P. A., (2006). A Brief Guide to Structural Equation Modeling. The Counseling Psychologist, 34(5), 719-751. doi: https://doi.org/10.1177/0011000006286345 [ Links ]
Yuan, K. H. (2005). Fit indices versus test statistics. Multivariate behavioral research, 40(1), 115-148. doi: https://doi.org/10.1207/s15327906mbr4001_5 [ Links ]
*E-mail: leonardo.medrano@ues21.edu.ar **E-mail: roger.munoz@uv.es
Recibido: 05-08-16
Revisado: 13-09-16
Aceptado: 16-03-17
Publicado: 05-05-17