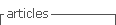Introducción
La tecnología cada vez va adquiriendo mayor importancia y presencia en el quehacer humano. Permite sostener una comunicación fluida con los diferentes actores sociales, sobre todo bajo el nuevo escenario con restricciones sanitarias, en donde es imprescindible su uso. En el ámbito educativo ha permitido continuar con el proceso de enseñanza y aprendizaje, especialmente en el área de matemáticas permitiendo diseñar modelos, simulaciones y experimentos que aportan al logro de los objetivos (Hegedus & Moreno-Armella, 2020; Santos-Trigo, 2020; Dalby & Swan, 2019; Trgalová et al., 2018), sin embargo se debe precisar que dicho recurso no reemplaza al docente, porque es quién diseña, desarrolla y realiza el seguimiento del avance académico, además que, cuando los resultados no son los esperados (Grisales, 2018), debe implementar nuevas estrategias y, a la vez, adquirir nuevas capacidades vinculadas a la tecnología (Castro et al., 2020; Hernández, 2017) que favorezcan más y mejor los procesos académicos en un contexto de mayor virtualidad y que exigen mayores retos tanto en la transmisibilidad como en la evaluación de las competencias (Vértiz Osores et al., 2020).
Desde esta perspectiva, la UNESCO tiene dentro de los objetivos estratégicos lograr la mejora de la calidad educativa, que no solo involucra a los contenidos, sino también a los métodos de enseñanza, que incluye la experimentación, innovación y la difusión de la información (Gavilanes, et al., 2019). Sin embargo, la experiencia en América Latina, que se inició por los 90s, estuvo centrada en la infraestructura tecnológica y la conectividad, razón por la cual cada país implementó diferentes políticas, sin siquiera sostenerse en objetivos estratégicos, ni operativos (Scagnoli, 2009; Oficina Regional de Educación para América Latina y el Caribe, 2013; Rama, 2014). El empeño estuvo centrado en adquirir recursos tecnológicos, implementación de redes y capacitación docente (Ministerio de Educación, 2017).
En el Perú, el estado a través del marco legal señala que las TICs constituyen un elemento fundamental en la formación académica, por ello se apoya en el avance de otros sectores, como es la alfabetización digital de todos los actores educativos. La historia evidencia que cada gobernante de turno ha implementado diferentes planes ‘innovadores’ sobre todo para el nivel educativo básico regular, que buscaron integrar estas herramientas en el proceso de enseñanza- aprendizaje, como por ejemplo el ‘Proyecto Huascarán’ (en 2001), una laptop por niño (en 2007), entre otros; centrados en vincular a los estudiantes con la tecnología teniendo como eje al docente. Sin embargo, no se ha logrado el objetivo, porque los ambientes educativos carecen de hardware, software, capacitación docente y un vínculo sostenido entre el Proyecto educativo Nacional y los planes implementados en las instituciones educativas (Ministerio de Educación, 2017), agudizándose el problema por la alta variabilidad en el acceso de energía y, sobre todo, a las líneas de conectividad especialmente en las regiones de sierra y selva.
El abordaje de la variable ‘resolución de problemas de figuras geométricas bidimensionales´ que se propone en esta investigación, responde a la inquietud que se manifiesta en el poco rendimiento que muestran los estudiantes universitarios desde su ingreso a sus carreras profesionales. Esta situación problemática, que vincula aspectos que van desde la aptitud de los estudiantes (Mason, 2003; Stenberg et al., 2010) hasta evidentes carencias en habilidades digitales para la enseñanza en muchos docentes (Manco-Chavez et al., 2020; Ocaña-Fernández et al., 2020), especialmente en el área de matemática (Kim et al., 2017; Ortega-Sánchez et al., 2020), son el reflejo de una débil formación básica, evidenciado en los resultados del Programa para la Evaluación Internacional de Estudiantes (PISA) (Benavides et al., 2014) en el cual Perú ocupa niveles bajos en el ranking internacional. Este preocupante escenario, al trasladarse al nivel educativo superior, empuja a la búsqueda de estrategias que faciliten la transmisión y aprehensión de las competencias mínimas de promoción estudiantil en su formación profesional. Dentro de estas competencias, el uso de softwares con aplicaciones específicas de enseñanza está evolucionando de necesario a imprescindible. Así, hay investigaciones donde se demostró que después de implementar el software GeoGebra se lograron mejoras en el rendimiento de estudiantes (Dikovic, 2009; Kutluca, 2013; Arbain & Shukor, 2015; Díaz-Nunja et al., 2018; Ramadhani & Dahlya Narpila, 2018; Septian et al., 2020; Ari Septian et al., 2020; Suryani et al., 2020) dándole múltiples aplicaciones que permitieron desarrollar estrategias adicionales de trabajo en equipo (Takači et al., 2015; Albano & Dello Iacono, 2019) y fomento de niveles positivos de motivación, cambiándoles favorablemente la actitud hacia las matemáticas (Zulnaidi & Zamri, 2017; Rohaeti & Bernard, 2018). Desde una perspectiva docente, también se tuvieron cambios positivos de las actitudes de enseñanza (Demirbilek & Žilinskienė, 2015), dando la posibilidad de organizar también hasta mejores materiales de instrucción (Saputra & Fahrizal, 2019).
Dentro de la concepción del aprendizaje significativo de Vygotsky (Marginson & Dang, 2017) es natural que las personas diariamente adquieran nuevos conocimientos. Los mismos que, en un escenario académico contemporáneo, son reforzados en las continuas sesiones de clase, apoyándose en el uso de software y hardware como medios para el logro de los objetivos (Orellana & Vilcapoma, 2018), desprendiéndose otros efectos positivos interpersonales como desarrollo de la habilidad del trabajo colaborativo (Helou & Newsome, 2018) y generación de más conocimiento en base al conocido, condición que fue ampliamente explicada por Ausbel (Getha-Eby et al., 2014; Ercan & Ural, 2016; Salazar, 2018). Otra teoría importante que refrenda este estudio fue de las situaciones didácticas (Brousseau, 2007; Antolin, 2010) la misma que indica que el docente es el responsable de las estrategias en el diseño, implementación y experiencia vinculadas al logro de los objetivos, desprendiéndose cuatro situaciones: a) acción: corresponde a la resolución del problema; b) formulación: involucra el diseño de diferentes situaciones para lograr la solución al caso o problema; c) validación: implica la intervención del maestro para reforzar lo desarrollado por el estudiante; d) institucionalización: compete al planteamiento de las convenciones sociales, formuladas a partir de la experiencia en la resolución de los problemas
En ese contexto, la importancia de la investigación no solamente se centra en la demostración de la efectividad del uso de este software libre en la mejora de las capacidades resolutivas de problemas de geometría (Ruiz, et al., 2012; Avilés, et al., 2015; Mudaly & Sheriff, 2016), sino que busca incrementar evidencia científica que refrende su uso en estudiantes universitarios que no pertenecen a especialidades de ciencia o ingeniería en un contexto de enseñanza eminentemente virtual, debido a las restricciones sanitarias por el Covid-19. Asimismo, pretende brindar mejores estrategias que mejore las condiciones motivacionales en los estudiantes, pudiendo también reducir los niveles de malestar y estrés en el personal docente (Vértiz-Osores et al., 2019). Ante lo expuesto, la objetivo propuesto fue determinar la efectividad del uso del software GeoGebra en la mejora de capacidades resolutivas de problemas de figuras geométricas bidimensionales en estudiantes universitarios de una carrera profesional de humanidades, contemplando como condiciones constantes de estudio a la comprensión de la casuística, el planteamiento, la aplicación de estrategias para el logro de la solución y la resolución misma, avalada por el análisis y la reflexión en todo el desarrollo de la pesquisa (Iriarte, 2011, Mazzilli, et al., 2016).
Metodología
La investigación está sustentada en el paradigma positivista (Ramos, 2015; Pérez, 2015). El enfoque fue cuantitativo (Sánchez, Reyes, & Mejía, 2018) y el método hipotético deductivo (Hernández-Sampieri & Mendoza, 2018). Fue aplicada (Del Canto & Silva, 2013; Sánchez, et al., 2018). Cuasiexperimental con dos grupos de personas del primer año de la carrera profesional de educación de una universidad privada en Lima (grupo Control = 29 estudiantes; grupo Experimental = 24 estudiantes). Solamente al grupo experimental se le suministró conocimientos de uso del software GeoGebra.
La evaluación se realizó en dos momentos (Antes de la aplicación del software = Pre test y, Después del uso de esa herramienta= Post test) (Hernández-Sampieri & Mendoza, 2018). El tiempo de realización de la investigación fue de 12 sesiones de clases a través de una plataforma virtual, divididas en dos sesiones por semana de tres (03) horas pedagógicas cada una (50 minutos de clase efectiva). Para la realización de los dos momentos de medición se emplearon pruebas de conocimientos (Cascaes, et al., 2015; Sánchez, et al., 2018), evaluando cuatro (04) dimensiones o componentes: a) D1 Resolución de problemas de áreas y perímetros de triángulos (6 ítems); b) D2 Resuelve problemas de áreas y perímetros de cuadriláteros (8 ítems); c) D3 Resuelve problemas relacionando áreas (3 ítems); d) Resuelve problemas de regiones sombreadas (3 ítems).
La escala empleada para la emisión de los resultados fue vigesimal (0 - 20), considerándose aprobado al estudiante con puntaje de evaluación igual o mayor que 10.5 (Minedu, 2020). Por otro lado, adoptando lo referido en el plan curricular de educación básica (Minedu, 2016) se hizo una clasificación categórica final de los estudiantes en base al puntaje obtenido (0 - 10.4 = Inicio; 10.5 - 14 = Proceso; 15 -20 = Logro). El análisis estadístico comparativo se hizo empleando la prueba paramétrica de medias T - Student para grupos independientes y la misma prueba para grupos pareados. La comparación de las categorías de clasificación se hizo mediante la prueba no paramétrica de rangos con signos de Wilcoxon (para el análisis de grupos pareados) y la prueba U - Mann Whitney (para las comparaciones de grupos independientes en cada momento de evaluación). Se empleó el software demo GraphPad Prism® Versión 9.
Resultados
a) Análisis de los componentes evaluados en la resolución de problemas de figuras geométricas bidimensionales
Como se indicó, se tuvieron en cuenta cuatro dimensiones, las mismas que, después de la prueba comparativa de grupos pareados evidenciaron diferencias significativas entre las mediciones antes (Pre test) y después (Post test) tanto para el grupo control como en el grupo experimental. No obstante, en la dimensión ‘Regiones sombreadas’ no hubo diferencias en contraste con las demás que mostraron diferencias, aunque no tan significativas (Figura 1). Una peculiaridad de este primer resultado es que los promedios de los calificativos no superaron a 11.45 (Resolución de áreas y perímetros de triángulos - post test), mientras que el menor promedio se vio en la dimensión ‘Resolución de áreas’ con un calificativo de 9.45. Por lo que, haciendo una diferencia entre ambos momentos de evaluación se tienen solamente dos puntos, siendo, evidentemente, estrecha la disparidad. Otro aspecto interesante fue que seis de ocho conjuntos de datos tuvieron un promedio superior al mínimo requerido como ‘Aprobatorio’ (Minedu, 2020), aunque se encontraron muy cerca del límite mínimo. Lo mejor de esto fue que, en todos los casos evaluados después de la primera medición se tuvo promedios aprobatorios, lo que evidencia que, después de todo, la metodología tradicional de enseñanza tiene efecto positivo.
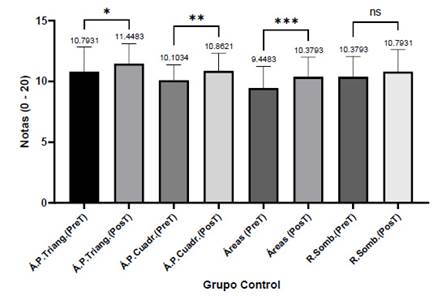
Por su parte, en el grupo experimental todas las comparaciones antes - después resultaron altamente significativas (Figura 2). Es notorio observar que, en las diferencias entre los grupos comparados, los promedios obtenidos tuvieron hasta un máximo de 4.29 puntos de incremento medio (en la dimensión ‘Resolución de áreas’) y un mínimo de 2.79 (en la dimensión ‘Resolución de áreas y perímetros de cuadriláteros’). Estos promedios evidencian mayor efectividad en los aprendizajes de los estudiantes, sin embargo, aún los promedios no superaron el puntaje ideal de 15.
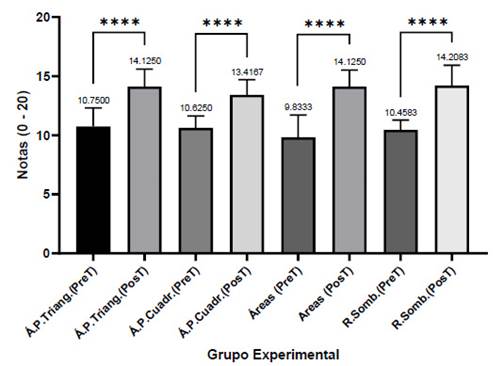
Asimismo, en los contrastes realizados se consideró comparaciones de los grupos ‘control’ y ‘experimental’ haciéndolas en cada uno de los dos momentos de evaluación (antes = Pre test y después = Post test). Definitivamente, los grupos comparados fueron independientes por lo que la prueba empleada también lo fue, obteniéndose que, en ninguno de los grupos comparados en el Pre test hubo diferencias significativas, teniendo promedios similares, estadísticamente hablando. Sin embargo, es importante señalar que cuatro de los ocho conjuntos de datos analizados mostraron promedios superiores al mínimo aprobatorio, acorde con lo estipulado por el Ministerio de Educación peruano. El menor promedio obtenido se observó en la dimensión ‘Resolución de áreas’ el grupo control (9.45) mientras que el mayor se vio en la dimensión ‘Áreas y perímetros de triángulos’ (10.79) (Figura 3).
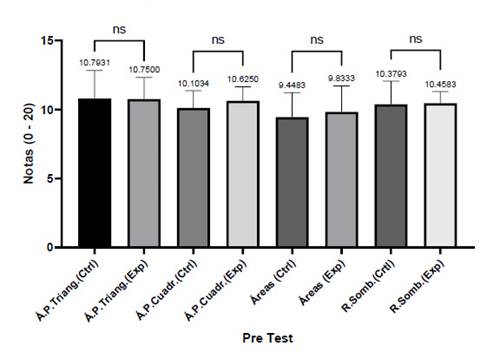
Figura 3 Comparaciones de las dimensiones por pares (Grupo control- Grupo experimental) en el momento antes de la aplicación del software GeoGebra (Pre test).
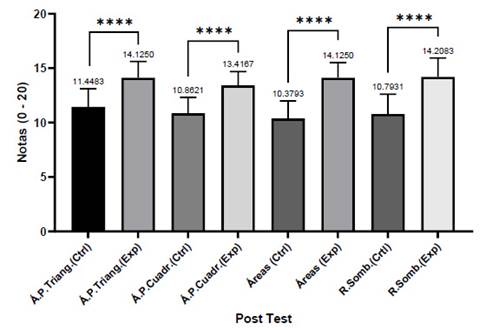
De manera similar a la comparación inmediata anterior, se hizo para el momento después (Post test) de la aplicación de la herramienta educativa, observando que hubo una alta significancia estadística para los cuatro contrastes. Es destacable indicar que el mayor promedio se obtuvo en la dimensión ‘Regiones sombreadas’ (14.21) del grupo experimental, aunque la mayor diferencia entre los grupos comparados se registró en la dimensión ‘Áreas’ en donde este mismo grupo fue 3.745 puntos en promedio más alto que su homólogo. En contraste, la menor diferencia estuvo entre los grupos de la dimensión ‘Áreas y perímetros de cuadriláteros’, en donde el grupo control fue 2.555 puntos menos que el experimental. Cabe mencionar también que en esta misma dimensión se observó el menor promedio de los datos del grupo experimental (13.42) (Figura 4)
b) Análisis de la evaluación en la resolución de problemas de figuras geométricas bidimensionales
En el análisis general se hizo comparaciones independientes (entre los grupos control y experimental para cada uno de los dos momentos de evaluación - Pre y Post test) y comparaciones pareadas de los grupos Control y experimental en su respectiva medición antes (Pre test) y después (Post test). En primer lugar, en las comparaciones independientes no hubo diferencias significativas entre los grupos control y experimental al inicio del experimento (Pre test), sin embargo, en la comparación final si lo hubo. Así se vio alta significancia entre los promedios de estos dos mismos grupos en el Post test. Lo que evidenció efectividad de la aplicación de la herramienta tecnológica en el grupo experimental que presentó el más alto promedio (14.04). Por otro lado, en las comparaciones pareadas se vio que hubo diferencias significativas tanto entre las evaluaciones pre y post del grupo control como en las del grupo experimental. Aunque la diferencia de este último grupo fue mucho más significativa, no se puede negar que el proceso de enseñanza per se marca una diferencia entre un antes y un después. El único problema es que ese cambio lo hace mucho más lento que cuando se usó el software.
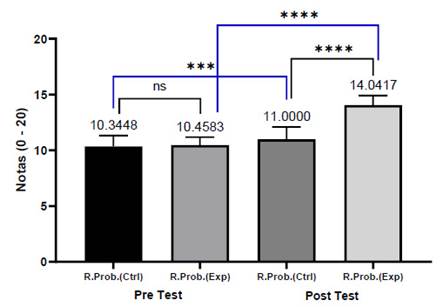
Figura 5 Comparaciones de la resolución de problemas de figuras geométricas (Grupo control- Grupo experimental: línea negra) en el momento antes y después (línea azul) de la aplicación del software GeoGebra.
Con la demostración cuantitativa de la efectividad del uso de este software, se realizó la categorización de los estudiantes en niveles estandarizados por el ministerio de educación del Perú, con la finalidad de distinguir mejor en cada uno de estos conglomerados. Siguiendo la misma lógica del análisis propuesto, se compararon los dos grupos de modo pareado. También se hizo la evaluación independiente en cada uno de los dos momentos de evaluación de cada uno de los grupos. Los resultados mostraron que no hubo diferencias entre las evaluaciones Pre y Post test en el grupo control, aunque en el grupo experimental si hubo diferencias entre los dos momentos, siendo mayor en el Post test (Z=--4.179). Por la otra parte, en las comparaciones independientes no se observó diferencias entre los grupos control - experimental en el Pre test a diferencia del Post test en donde hubo diferencia estadística del grupo experimental sobre el grupo control (Z = -4.9531). Esto corrobora que hubo una mejora de puntajes en el grupo post test, lo mismo que elevó el porcentaje de estudiantes en los niveles de logro en el grupo experimental, siendo el único grupo de datos que mostró esa variación (Tabla 1).
Tabla 1 Comparaciones de los resultados de la categorización de los estudiantes en base a la evaluación de resolución de problemas de figuras geométricas.
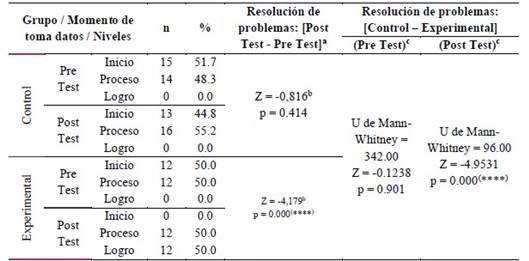
a. Prueba de rangos con signo de Wilcoxon (Grupos pareados) b. Se basa en rangos negativos. c. Prueba U Mann Whitney (Grupos independientes). (****) = p<0.001
Discusión
En términos de cumplimiento de objetivos y demostración de lo que se quería hacer, se indica que se cumplieron a cabalidad y quedó evidenciada la efectividad de esta herramienta informática, coincidiendo con otros trabajos científicos que tuvieron un diseño similar (Takači et al., 2015; Zulnaidi & Zamri, 2017; Rohaeti & Bernard, 2018; Alcívar-Castro, 2019; Ari Septian, Inayah, et al., 2020; Ari Septian, Sugiarni, et al., 2020), empero, es importante señalar que hubo diferencias significativas entre los grupos control y experimental (pareados) comparados en los dos momentos de toma de datos lo que evidencia también un cambio favorable en el proceso de aprendizaje de los estudiantes producto de la secuencialidad temática de la educación mediante el método convencional, lo mismo que es natural y fundamenta lo realizado en los planes curriculares universitarios hasta la fecha. Aunque, teniendo en cuenta el contexto de distanciamiento social que obliga a la realización de clases remotas quedan muchos aspectos que clarificar en los procesos formativos estudiantiles, como la evaluación que refleje las competencias matemáticas previstas en los estudiantes post capacitación (Stacey & Wiliam, 2013; Vértiz Osores et al., 2020) y la garantía de la realización de investigación científica genuina sin caer en la estática del facilismo por el uso creciente de herramientas tecnológicas que simplifican más los procesos académicos (Niess, 2005; Lavicza, 2010; Ropohl et al., 2018).
Por otra parte, en el proceso de ejecución experimental de las sesiones de clase se percibieron dificultades vinculados con procesos de comunicación, lo que podría atribuirse a la conectividad o la condición remota de la impartición del conocimiento, sin embargo, fue notorio que el ritmo de aprendizaje se ralentizó debido a factores no controlados por los docentes y que podría atribuirse a una condición de desigualdad en la adaptación de los hogares a la educación remota (Bacher-Hicks et al., 2021). Al comienzo, esto obligó a repetir los tópicos y procedimientos de manejo del software para lograr una mayor comprensión. Ante esta situación, fue necesario emplear estrategias de trabajo colaborativo, las mismas que permitieron un interaprendizaje, observando que el proceso de enseñanza de los pares tuvo mayor eficacia, en términos de tiempo de aprendizaje, además de generar un clima agradable y motivador entre ellos, en un espacio virtual por supuesto. Esto es explicable en la naturaleza socializadora del humano y en la generación de conocimiento a partir del mismo (Getha-Eby et al., 2014; Ercan & Ural, 2016; Salazar, 2018) adicionando al aprendizaje individual como resultado del proceso grupal (Kaye, 1992; Horwitz et al., 2017; Cui et al., 2020). Este nuevo entorno de socialización continuada en las fases de instrucción académica brinda nuevos horizontes a los docentes, quienes no solamente se reinventan sobre la marcha, sino que distinguen procesos de socialización que favorecen las habilidades de manejo de herramientas que conducen hacia metodologías que facilitan la metacognición. Otra de las ventajas que se ha observado durante la ejecución de este trabajo es que se tiene mayor posibilidad de generar autonomía de aprendizaje en los estudiantes debido que las asignaciones académicas asincrónicas involucraron el uso del software GeoGebra (para el grupo experimental) dando opción a la autorregulación del aprendizaje, que fue más evidente en las mujeres, aunque no se visualizaron en los resultados de este estudio. Este aspecto podría ser tratado en detalle por futuras investigaciones pues brinda una puerta de posibilidades de análisis, como también lo sugirió Wijaya et al. (2020). Finalmente, una de los efectos que se está observando después del inicio de la pandemia por Covid-19 es que, muy probablemente, el aprendizaje digital de las matemáticas quede como una parte constitutiva del proceso de enseñanza -aprendizaje en las universidades y otros centros de formación académica (Mulenga & Marbán, 2020; Radha et al., 2020), facilitando la exploración de otros aspectos complementarios como el empleo de realidad virtual que permita poner en práctica la teoría explicada y desarrollada en las fases formativas de las matemáticas (Lamb & Etopio, 2020; Rosa & Pinheiro, 2020; Simonetti et al., 2020).
Conclusión
El uso del software GeoGebra representó una excelente opción para la mejora de las habilidades resolutivas de problemas vinculados con figuras geométricas bidimensionales en la asignatura de matemáticas para estudiantes universitarios del primer año de la carrera profesional de educación, brindando la oportunidad de desarrollar estrategias de trabajo colaborativo, integración socio estudiantil y mejora del clima de clase en un contexto de interacción académica remota. Se recomienda el empleo de esta herramienta, aunque podría ampliarse con la combinación de otras aplicaciones más que facilitarían el proceso de enseñanza aprendizaje.