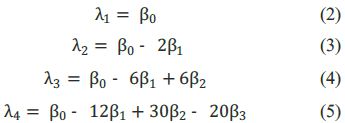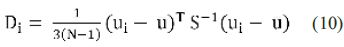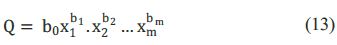Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO  uBio
uBio
Compartir
Revista de Investigaciones Altoandinas
versión On-line ISSN 2313-2957
Rev. investig. Altoandin. vol.19 no.2 Puno abr./jun. 2017
http://dx.doi.org/10.18271/ria.2017.281
REPORTE DE CASO
Regionalización de Caudales Mensuales en la Región Hidrográfica del Titicaca, Perú
Regionaliatión of Monthly Flows of the Titicaca Hydrographic Region, Perú
Apolinario Lujano Laura1*, José Pitágoras Quispe Aragón1, Efraín Lujano Laura2, Bernardino Tapia Aguilar3
1 Autoridad Nacional del Agua – Perú;
2 Universidad Peruana Unión – Perú;
3 Servicio Nacional de Meteorología e Hidrología –Perú.
* Autor para correspondencia:Apolex23@gmail.com
RESUMEN
La presente investigación se realizó en la Región Hidrográfica del Titicaca, Perú. El objetivo principal fue desarrollar modelos regionales de caudales medios mensuales y de persistencia de los principales ríos, aplicado a la problemática de la estimación de caudales en cuencas sin registro hidrométrico. Se tomaron como variables independientes las características climáticas y fisiográficas de las cuencas en estudio y como variable dependiente los caudales medios mensuales y de persistencia. La metodología para identificar regiones hidrológicas homogéneas fueron realizados a través de las técnicas de Ward y Momentos-L. Las ecuaciones regionales se determinaron utilizando modelos de regresión potencial, siendo las variables explicativas el área de la cuenca y la longitud del río principal. Para la evaluación de la significancia estadística de los modelos regionales se utilizó los indicadores de eficiencia de Nash-Sutcliffe (NSE) y la raíz del error cuadrático medio (RMSE). Las ecuaciones regionales propuestas muestran un buen desempeño y estiman los caudales observados.
PALABRAS CLAVES: Método de Ward, Momentos - L, regionalización, regresión potencial.
ABSTRACT
This research was conducted in the Hydrographic Region Titicaca, Peru. The main objective was to develop regional models of average monthly flows and persistence of the main rivers, applied to the problem of estimation of flows in basins without hydrometric registration. The climatic and physiographic characteristics of the basins under study were taken as independent variables and the mean monthly flows and persistence as a dependent variable. The methodology to identify homogeneous hydrological regions was made through the techniques of Ward and L-Moments. The regional equations were determined using potential regression models, the explanatory variables being the basin area and the length of the main river. The Nash-Sutcliffe (NSE) efficiency indicators and the root mean square error (RMSE) were used to assess the statistical significance of the regional models. The proposed regional equations show a good performance and estimate the observed flows.
KEY WORDS: Ward Method, L-moments, regionalization, potential regression.
INTRODUCCIÓN
El conocimiento de la oferta hídrica de una cuenca es de relevante importancia para una adecuada gestión de los recursos hídricos, sin embargo, la información hidrológica no siempre se encuentra disponible, por el número limitado de estaciones hidrométricas y el periodo de los registros, combinado con una falta de metodología regional apropiada a nuestro medio, que permita conocer el volumen disponible en forma mensual en cuencas no aforadas.
Para la estimación de caudales es necesario el conocimiento de datos históricos, pero, muchas veces esas informaciones no están disponibles en los lugares de interés (Pandey & Nguyen, 1999). Siendo la estimación de los caudales en una cuenca sin información uno de los problemas de la ingeniería hidrológica (Hall & Minns, 1999), agravándose por la poca cantidad de cuencas aforadas, la discontinuidad de las series y la confiabilidad de los datos disponibles (Paris & Zucarelli, 2004). La regionalización de caudales es una técnica utilizada para suplir la falta de información hidrológica en lugares con poca disponibilidad de datos (Rao & Srinivas, 2006). Asimismo, tiene como propósito facilitar la transferencia de información hidrológica a cuencas sin registro, en los cuales se requieren mediciones, y que pertenecen a una misma región hidrológica (Nathan & McMahon, 1990; Franchini & Suppo, 1996). Los modelos de regionalización son basados en las características fisiográficas y climáticas de una región de interés (Dalrymple, 1960; Tucci et al., 1995; Ourda et al., 2001, Falco et al., 2012).
La metodología de regionalización involucra dos etapas principales: la identificación de cuencas homogéneas y la aplicación de un método regional para cada región homogénea (Ouarda et al., 2007, Malekinezhad et al., 2011). Estudios realizados para la delimitación de regiones homogéneas mediante el método de momentos-L se puede citar a Saff (2010), Malekinezhad et al. (2011), y constituye la etapa más difícil para obtener una solución regional satisfactoria (Gingras & Adamowski, 1993). La técnica de regionalización hidrológica ha sido aplicada en varios estudios con buenos resultados Euclydes et al. (2001); Da Silva et al. (2003); Sanbom & Bledsoe (2006); Lujano et al. (2016), utilizaron modelos de regresión lineal y potencial para la estimación de caudales medios y de persistencia siendo la variable que explica los caudales, el área de la cuenca. Halcrow (2011) obtiene resultados en la región hidrológica del Titicaca, la variable significativa en el estudio resultó el área de la cuenca, mientras que De Andrade et al. (2004) al regionalizar los caudales medios mensuales concluyen que la variable explicativa es el área de la cuenca; Álvares et al. (2011) obtuvieron un modelo regional, determinando que las variables explicativas son el área de la cuenca y la precipitación mediaanual.
La regionalización es un tema de importancia que toma énfasis en la solución de estimar estos valores en cuencas sin información a partir de ecuaciones regionales, establecidos con información de cuencas aforadas, y cuyo objetivo fue desarrollar modelos regionales de caudales medios mensuales de los ríos de la Región Hidrográfica del Titicaca, Perú. Los resultados servirán como una alternativa para estimar y evaluar la disponibilidad del agua superficial en cuencas no aforadas, así mismo como punto de partida para nuevas propuestas de investigación en regionalización hidrológica.
MATERIALES Y MÉTODOS
Área de estudio
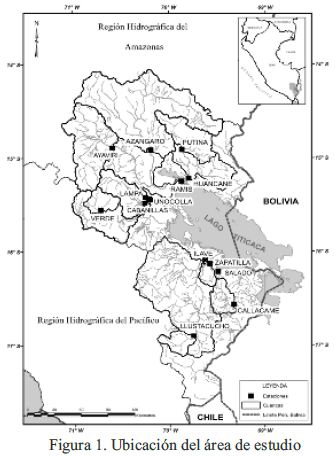
La zona de estudio abarca la región hidrográfica del Titicaca – Perú, según el estudio de codificación de Pfafstetter. Tiene como límites por el norte con la región hidrográfica del Amazonas, por el Este y sur con la región hidrográfica del Pacífico y por el Oeste con la República de Bolivia. (Figura 1).
Geográficamente, está comprendida entre las coordenadas UTM (WGS 84 Zona 19 Sur) Este: 271,808 m a 496,791 m y Norte: 8'104,832 m a 8'443,369 m.
Datos utilizados
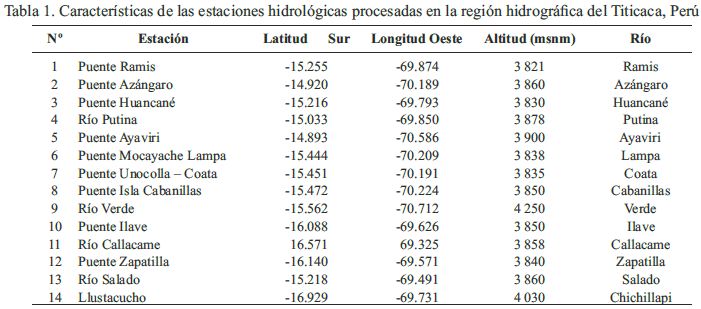
Los datos recopilados son los caudales medios mensuales correspondientes a los años 1969 - 2013. La muestra está constituida por las estaciones hidrológicas (Huancané, Ramis, Coata, Verde e Ilave) y las estaciones de corto periodo de registro (Putina, Azángaro, Ayaviri, Lampa, Zapatilla, Salado, Callacame) ubicadas dentro de la zona de estudio, administradas por el Servicio Nacional de Meteorología e Hidrología (SENAMHI) y la estación Llustacucho en el río Chichillapi información de caudales extraída del estudio realizado por la Autoridad Nacional del Agua (ANA), la estación Llustacucho, fue registrada por el Proyecto Especial Tacna (PET). En la Tabla 1 se muestran las características de las estaciones en estudio.
Identificación de regiones homogéneas
Método de conglomerado
Ward (1963), indica que es un método de agrupación jerárquica basado en la minimización de la distancia euclidiana en el sitio o espacio característico dentro de cada grupo. Un método jerárquico crea una descomposición jerárquica de un conjunto de datos, formando un dendograma (árbol) que divide el conjunto de datos en grupos más pequeños (Jain et al., 1999). Ward (1963), menciona que el algoritmo de Ward es una técnica de uso frecuente para los estudios de regionalización en la hidrología y la climatología. Se basa en el supuesto de que, si se fusionan dos grupos, la consiguiente pérdida de información, o el cambio en el valor de la función objetivo, dependerán sólo de la relación entre los dos grupos combinados y no en las relaciones con otros grupos.
La identificación de regiones homogéneas mediante este método se basa en las recomendaciones de Gottschalk (1985), Nathan & McMahon (1990), Hosking & Wallis (1997) y Zhang & Hall (2004), método jerárquico que no requiere del conocimiento anticipado de un grupo homogéneo.
Método de momentos -L
Los momentos–L, fueron introducidos por Hosking & Wallis (1997), constituyen un sistema alternativo para describir las formas de las funciones de distribución de probabilidades, y surgen de combinaciones lineales de los momentos ponderados probabilísticamente (MPP) introducidos por Greenwood et al. (1979).
Los momentos de probabilidad ponderada están definidos (Hosking, 1990) por:
Br = E^{X[Fx(X)]r} (1)
Donde:
Fx (x) es la función de distribución acumulativa de x. Cuando r = 0, βr es equivalente a la media.
Los primeros cuatro momentos – L de cualquier distribución son calculados como:
El momento - L de primer orden λ1 , es la media de la distribución y se determina de forma análoga a los momentos convencionales. El segundo, es la medida de escala o desviación estándar λ2.
Las relaciones de los momentos-L son análogas a los momentos estadísticos convencionales, y se expresan como:
Medida de discordancia (D)
Hosking & Wallis (1997) proponen la medida de discordancia D, para identificar estaciones cuyos valores muestrales de los momentos-L difieren significativamente del resto de las estaciones de la supuesta región. La medida de discordancia para la estación i se expresa según:
donde T es el superíndice que indica la matriz transpuesta, S-1 es la matriz inversa de covarianza, N es el número de estaciones de observación de una región.
Valores elevados de D, son característicos de estaciones que se apartan del comportamiento general del resto de las estaciones. Hosking & Wallis (1997) sugieren que valores de D ≥ 3 identifican estaciones inusuales con respecto al comportamiento del resto de las estaciones, aunque siempre es aconsejable revisar las estaciones, que aun no alcanzando dicho valor, presenten valores mayores.
Prueba de Heterogeneidad (H)
Propuesta por Hosking & Walis (1997), compara las variaciones entre las diferentes estaciones, de los momentos-L muestrales. Un estadístico apropiado para comparar las dispersiones observadas y las simuladas es la medida de heterogeneidad H que se expresa a continuación:
donde uv es la media, σv la desviación estándar y Una región es declarada como "aceptablemente homogénea" si "posiblemente heterogénea" si 1≤H<2, y "definitivamente heterogénea" si H≥2.
Ecuaciones de regresión potencial
Tucci (2002), propone la regionalización de caudales en base al análisis de regresión, el cual procura inferir una relación matemática entre una variable dependiente y una o más variables independientes, la regresión lineal múltiple se define de la siguiente manera:
Q= b0 +b1x1+b2x2+...+ bmxm (12)
Los coeficientes de ajuste b 0 a b m de la ecuación anterior, se obtienen minimizando la suma de los cuadrados de los residuos. La regresión lineal múltiple tiene pocas aplicaciones como modelo empírico y en general, es mucho más utilizado el modelo de regresión potencial (McCuen et al., 1990; Pandey & Nguyen, 1999; Topaloglu, 2000; Merz & Blöschl, 2004; Sanborn & Bledsoe, 2006; Lujano et al., 2016) cuya expresión es:
El modelo se vuelve lineal aplicando logaritmos en ambos lados de la ecuación, obteniéndose:
LnQ =Lnb0+ b1Lnx1+ b2Lnx2+ ...+ bmLnxm (14)
La solución de la ecuación se obtiene por el método de los mínimos cuadrados obteniendo los coeficientes de ajuste bi con i = 1,2,3,…,m. Haciendo a0 = Ln b0 de la ecuación, entonces el valor de b0 será igual a eao para los logaritmos naturales. Siendo la solución óptima en el dominio logarítmico (McCuen et al., 1990).
Evaluación estadística de los modelos regionales
Los índices estadísticos utilizados para evaluar el desempeño de los modelos regionales fueron la eficiencia de Nash (NSE) propuesto por Nash – Sutcliffe (1790) y la raíz del error cuadrático medio (RMSE); usados comúnmente para la evaluación de modelos matemáticos.
Donde: Уi es el valor observado, ŷi es el valor calculado, ŷ es el promedio de los datos observados y N es el número de datos observados.
La clasificación del (NSE) se realizó según las discreciones de Ritter & Muñoz (2013). La Raíz del error cuadrático medio (RMSE) se cuantificó en términos de las unidades de la variable calculada, indicador usado frecuentemente Legates & McCabe (1999).
RESULTADOS Y DISCUSIONES
Identificación de regiones homogéneas
Método de conglomerado
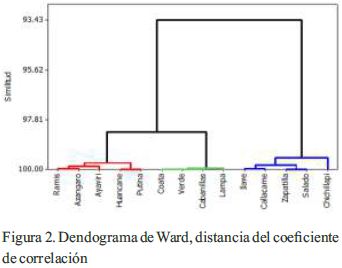
En la Figura 2, se muestra el agrupamiento de estaciones basado en el análisis de conglomerados cuya representación es a través del dendograma, considerándose el método de Ward, con una agrupación de 3 clusters, basados en la medición de la distancia del coeficiente de correlación, del cual se infiere que los grupos de estaciones responden a una similitud cercana entre cada sub-región homogénea.
En el dendograma se observa tres grupos de estaciones asociadas, coincidiendo en la existencia de tres sub-regiones homogéneas dentro de la región hidrológica homogénea determinada por Halcrow (2011).
Método de Momentos-L
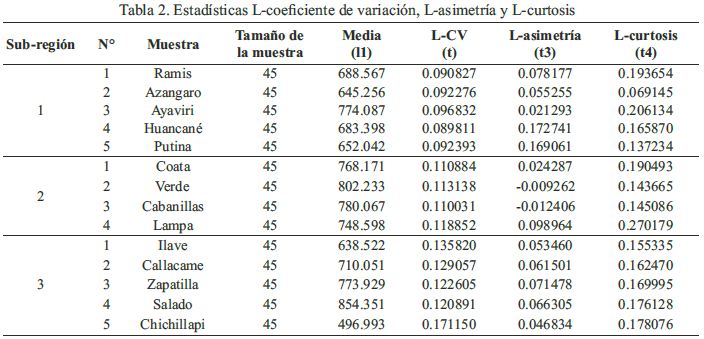
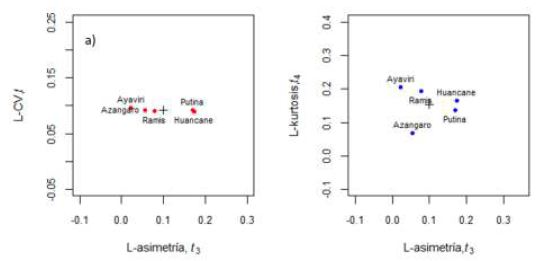
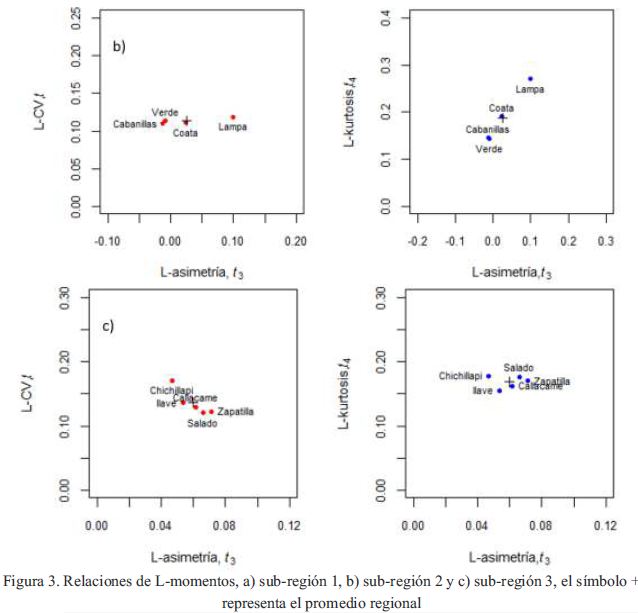
Las sub-regiones homogéneas preliminares identificadas por el algoritmo de Ward, son controladas por pruebas basadas en dispersión L-Cv, L-asimetría, L-curtosis, pruebas de discordancia y heterogeneidad. En la Tabla 2, se muestran las estadísticas de L-momentos (Media, L-coeficiente de variación, L-asimetría y L-curtosis), mientras que en la Figura 3 se aprecia los diagramas de dispersión de las relaciones L-coeficiente de variación con Lcurtosis y L-asimetría con L-curtosis, deduciéndose que ninguna estación se encuentra alejada de manera significativa del promedio, por lo tanto se consideran como sub-regiones homogéneas.
Medida de discordancia
En la Tabla 3, se muestra que, para las sub-regiones homogéneas 1, 2 y 3, se tiene una discordancia crítica (Dc) igual a 1.33, 3.00 y 1.33 respectivamente. Los resultados obtenidos son aceptables según Hosking & Wallis (1997).
Prueba de heterogeneidad
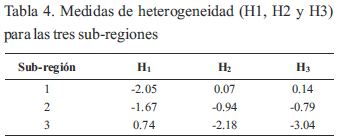
Se establecieron tres sub-regiones homogéneas, con valores de H de -2.05, -1.67 y 0.74 para las subregiones 1, 2 y 3, los cuales satisfacen la condición de aceptablemente homogénea (H<1). La Tabla 4, muestra la prueba de heterogeneidad, cuyos resultados son aceptables según Hosking & Wallis, (1997). Se observa que los valores de H1 son inferiores al umbral de homogeneidad (H<1).
Modelos regionales de caudales medios mensuales
Los modelos regionales propuestos para las subregiones homogéneas 1 y 3, está asociado al área de la cuenca (A) en Km2, las ecuaciones son válidas para cuencas con áreas comprendidas entre 1836.8 Km2 ≤ A (Km2) ≤ 14676.7 Km2, para el caso de la sub-región 1. Mientras que para la sub-región 3 los modelos están asociados a la misma variable explicativa, que muestran validez para cuencas con áreas entre 392.0 Km2 ≤ A (Km2) ≤ 7771.5 Km2.
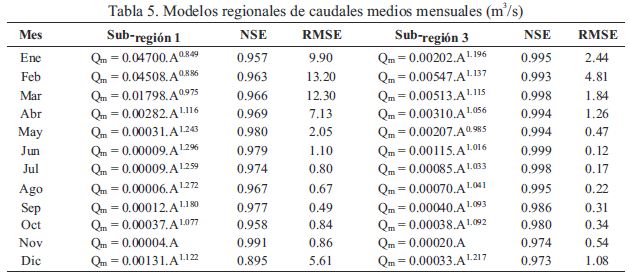
La Tabla 5 muestra las ecuaciones regionales, recomendadas para la estimación del caudal medio mensual en cada sub-región homogénea.
Los resultados muestran una gran regularidad en las estimaciones, lo cual está asociado a la veracidad de la variable fisiográfica de cada cuenca (área). Álvares et al. (2011) en su trabajo de investigación concluyen que las variables de mayor influencia en el comportamiento de los gastos son la longitud del cauce principal, el área de la cuenca y la precipitación anual. Asimismo, Da Silva et al. (2003), Euclydes et al. (2001), consideran como variable que mejor explica los caudales el área de la cuenca, corroborados también por Sanborn & Bledsoe (2006), De Andrade et al. (2004), Malekinezhad et al. (2011), Halcrow (2011), Lujano et al. (2016).
Los resultados de la evaluación estadística, para los modelos regionales propuestos en la sub-región 1 estiman valores similares a los observados, la evaluación estadística mediante la eficiencia de Nash (NSE) varían entre 0.895 a 0.991, considerados como buenos a muy buenos según las discreciones de Ritter & Muñoz (2013). Mientras que en términos de error (RMSE) varia de 0.49 m3/s a 13.20 m3/s.
En cuanto a los modelos regionales propuestos para la sub-región 3 la evaluación estadística mediante la eficiencia de Nash (NSE) varía entre 0.973 a 0.999, según Ritter & Muñoz (2013) los modelos regionales se clasifican como muy buenos siendo superiores a 0.90 para todos los meses. Sin embargo, en términos de error los valores de (RMSE) resultaron entre 0.12 m3/s a 4.81 m3/s.
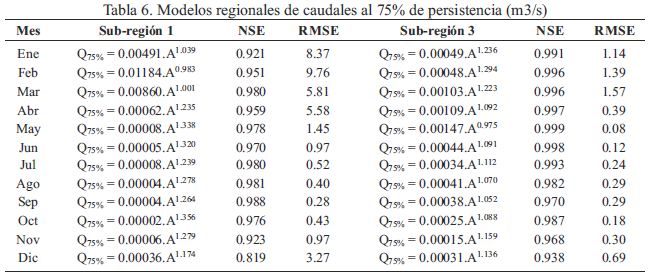
Modelos regionales de caudales al 75% de persistencia En la tabla se muestra los modelos regionales del tipo potencial, recomendados para la estimación del caudal al 75% de persistencia para cada sub-región homogénea.
Los modelos propuestos están asociados al área de la cuenca corroborado en los estudios realizados por Euclydes et al. (2001), Lujano et al. (2016), donde consideran como la variable que mejor explica los caudales al 75% de persistencia. Los resultados de la evaluación estadística de los modelos regionales propuestos para la sub-región 1, según la eficiencias de Nash (NSE) varía entre 0.819 a 0.988, según las discreciones de Ritter & Muñoz (2013) se clasifican como buenos a muy buenos. Mientras que en términos de error los valores de (RMSE) resultaron de 0.28 m3/s a 9.76 m3/s.
Los resultados de la evaluación estadística para los modelos regionales Q75% de persistencia propuestos para la sub-región 3, según la eficiencia de Nash (NSE) varían entre 0.938 a 0.999, resultados considerados como muy buenos según las discreciones de Ritter & Muñoz (2013). En términos de error (RMSE) resultaron valores de 0.08 m3/s a 1.57 m3/s.
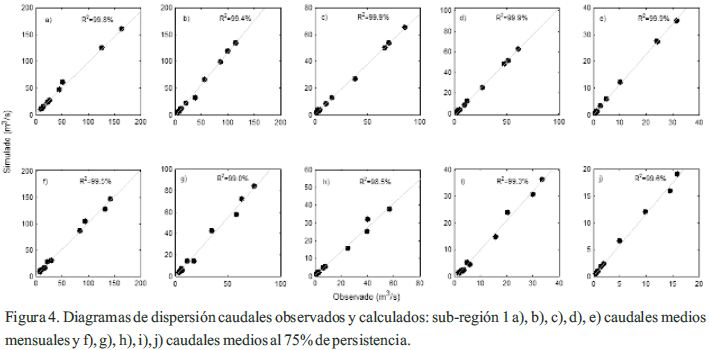
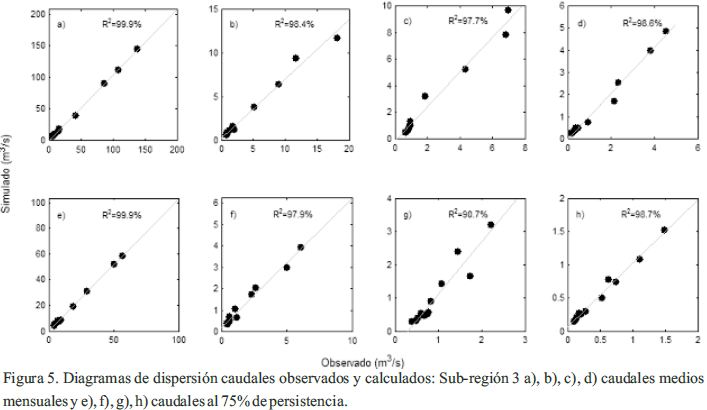
Los diagramas de dispersión de caudales medios mensuales y al 75% de persistencia observados y calculados, se observa en la Figura 4 y 5, deduciéndose que los caudales se relacionan.
CONCLUSIONES
En la investigación se determinó tres sub-regiones homogéneas en la región hidrográfica del Titicaca en el lado peruano, utilizando el método de Ward que permitió estimar a priori las sub-regiones homogéneas y validadas con la metodología momentos-L, dentro de las cuales es válido transferir información. Sin embargo, sólo para las sub-regiones homogéneas 1 y 3, se obtuvieron los modelos regionales.
Se propuso modelos regionales de caudales medios mensuales y de persistencia, siendo la variable explicativa el área de la cuenca (A). Los modelos regionales propuestos permitirán estimar en cualquier punto de interés de las cuencas sin información los caudales medios mensuales y de persistencia, considerando como variable de ingreso el área de la cuenca (A) en Km2. Los modelos regionales propuestos en la presente investigación podrán ser aplicados en los rangos de área que fueron estimados, para cuencas sin registro de caudales según sub-región homogénea.
REFERENCIAS BIBLIOGRÁFICAS
Dalrymple, T. (1960). Flood – Frequency Analyses. Manual of Hydrology: Part 3. Flood-Flow Techniques. Geological Survey Water-Supply Paper 1543-A. United States Government Printing Office, Washington. [ Links ]
Da Silva, J.O.B., De O. Bueno, E., Tucci, C.E.M., & Castro, N.M.R. (2003). Extrapolação Espacial na Regionalização da Vazão. Revista Brasileira de Recursos Hídricos, 8(1), 21-37. [ Links ]
De Andrade, E., Menezes, M., Tavora, R., Meireles, M., & Nieto, J. (2004). Regionalização de modelos de vazões medias de longo periodo para o Estado do Ceará. Revista Ciencia Agronòmica, 35, 139-148. [ Links ]
Euclydes, H.P., Ferreira, P.A., Og Arao, V.R., & Medeiros, D.R. (2001). Regionalização Hidrológica na Bacia do Alto São Francisco a Montante da Barragem de Três Marias, Minas Gerais. Revista Brasileira de Recursos Hídricos, 6(2), 81-105. [ Links ]
Falco, P.F., De Araujo, N.A., Silva, R.F., & Fernandes, D.S.M. (2012). Extrapolacao de equacoes de regionalizacao de vazoes mínimas: Alternativas para atenuar os riscos. Water Resources and Irrigation Management, 1(1), 51-59. [ Links ]
Franchini, M., & Suppo, M. (1996). Regional analysis of flow duration curves for a limestone region, Water Resource Management, 10, 199–218. [ Links ]
Gingras, D., & Adamowski, K. (1993). Homogeneous Region Delineation Bases on Annual Flood Generation Mechanism. Hydrological Sciences Journal, 38(2), 103-121. [ Links ]
Gottschalk, L. (1985). Hydrological regionalization of Sweden. Hydrology Science Journal, 30, 65–83. [ Links ]
Greenwood, J.A., Landwehr, J.M., Matalas, N.C., & Wallis, J.R. (1979). Probability weighted moments: definition and relation to parameters of several distributions expressible in inverse form. Water Resources Research, 15(5), 1049-1054. [ Links ]
Halcrow, (2011). Atlas del Potencial Hidroeléctrico del Perú. Lima – Perú [ Links ].
Hall, M.J., & Minns, A.W. (1999). The Classification of Hydrologically Homogeneous Regions. Hydrological Sciences Journal. 44(5), 693-704. [ Links ]
Hosking, J. (1990). L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Statics. Soc. B. 52, 105-124. [ Links ]
Hosking, J., & Wallis, J. (1997). Regional Frecuency Analysis: An Approach Base on L-Moments. Cambridge University Press, Cambridge, New York, Melbourne, Madris, Cape Town, Singapore, Sao Paulo. 224, 100 – 123.
Jain, A.K., Murty, M.N., & Flynn, P.J. (1999). Data Clustering. A Review. ACM Computing Surveys, 31(3), N° 3.
Legates, D. R., & McCabe, G. J. (1999). Evaluating the use of goodness-of-fit measures in hydrologic and hydroclimatic model validation. Water Resources Research, 35(1), 233–241. [ Links ]
Lujano, A., Lujano, E., & Quispe, J.P. (2016). Regionalización de caudales anuales en cuencas del altiplano peruano. Revista de Investigaciones Altoandinas, 18(2), 189-194. [ Links ]
Malekinezhad, H., Nachtnebel, H.P., & Klik, A. (2011). Comparing the index-flood and multiple-regression methods using L-moments. Physics and Chemistry of the Earth, 36, 54-60. [ Links ]
McCuen, R.H., Leahy, R.B., & Johson, P.A. (1990). Problems with Logarith-mic Transformations in Regression. Journal of Hydraulic Engineering, 116(3), 414-428. [ Links ]
Merz, R., & Blöschl, G. (2004). Regionalization of catchment model parameters. Journal of Hydrology, 287, 95-123. [ Links ]
Moriasi, D.N., Arnold, J.G., Van Liew, M.W., Bingner, R.L., Harmel, R.D., & Veith, T.L. (2007). Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulation. Transactions of the ASABE, 50(3), 885-900. [ Links ]
Nash, J.E., & Sutcliffe, J.V. (1970). River flow forecasting through conceptual models, part I: A discussion of principles. Journal of Hydrology, 10(3), 282–290. [ Links ]
Nathan, R.J., & McMahon, T.A. (1990). Identification of homogeneous regions for the purpose of regionalization. Journal of Hydrology, 121, 217-238. [ Links ]
Ourda, T.B.M.J., Bá, K.M., Díaz-Delgado, C., Carsteanu, A., Chokmani, K., Gringas, H., Quentin, E., Trujillo, E., & Bobee, B. (2008). Intercomparison of Regional Flood Frecuency Estimation Methods at Unaguged Sitios for a Mexican Case Study. Journal of Hydrology, 348, 40-58. [ Links ]
Pandey, G.R., & Nguyen, V.T.V. (1999). A comparative study of regression based methods in regional frequency analysis. Journal of Hydrology, 225, 92-101. [ Links ]
Paris, M.C., & Zucarelli, G.V. (2004). Regionalización de caudales. Propuesta metodológica para la identificación de regiones homogéneas. Ingeniería hidráulica en México, 19(4), 5-19. [ Links ]
Rao, A.R., & Srinivas, V.V. (2006). Regionalization of watersheds by hybrid cluster analysis. Journal of Hydrology, 318, 37–56. [ Links ]
Ritter, A., & Muñoz, R. (2013). Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. Journal of Hydrology, 480, 33-45. [ Links ]
Saf, B. (2010). Asseement of the effects of discordant sites on regional flood frecuency analysis. Journal of Hydrology, 380, 363-375. [ Links ]
Sanborn, S.C., & Bledsoe, B. P. (2006). Predicting streamflow regime metrics for ungauged streams in Colorado, Washington, and Oregon. Journal of Hydrology, 325, 241–261 [ Links ]
Topaloglu, F. (2000). Estimation of Instantaneous Peak Flows in Seyhan River Basin Using Regional Regression Procedures. Turk J Agric For, 26, 47-55. [ Links ]
Tucci, C. (2002) Regionalização de Vazões. Primera edição. Ed. Universidades/UFRGS, Brasil. 256 pp. [ Links ]
Ward, J.H., (1963). Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc, 58, 236–244. [ Links ]
Zhang, J., y Hall, M.J. (2004). Regional flood frequency analysis for the Gan-Ming River basin in China. Journal of Hydrology, 296, 98–117. [ Links ]
Artículo recibido 03/03/2017
Artículo aceptado 20/06/2017
On line: 26/06/2017