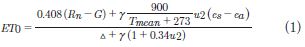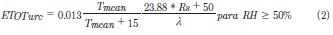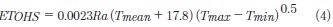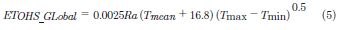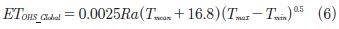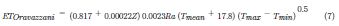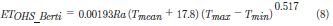REPORTE DE CASO

 

Métodos alternativos de estimación de evapotranspiración de referencia en la estación de Yauri – Cusco, Perú

Alternative methods of estimation of reference evapotranspiration in the Yauri station – Cusco, Peru

 

Apolinario Lujano^1*, José P. Quispe¹ & Efrain Lujano²

¹Autoridad Nacional del Agua, ANA, Autoridad Administrativa del Agua Pampas Apurímac, Apurímac - Perú

²Escuela profesional de Ingeniería Agrícola, Universidad Nacional del Altiplano, Puno – Perú

^*Autor para correspondencia: Apolinario Lujano, e-mail: apolex23@gmail.com

Apolinario Lujano https://orcid.org/0000-0002-9386-1613

José P. Quispe https://orcid.org/0000-0002-8556-8927

Efrain Lujano https://orcid.org/0000-0002-6543-8324

 

---

RESUMEN

La evapotranspiración de referencia (ΕΤo) es un componente principal del ciclo hidrológico y su estimación es esencial para el requerimiento neto de riego, la planificación y la gestión de los recursos hídricos regionales. El objetivo fue evaluar el desempeño de diferentes métodos empíricos para estimar la evapotranspiración de referencia y proponer una alternativa para estimar la ETo en casos de limitación de datos meteorológicos en la estación meteorológica de Yauri. La metodología consistió en comparar los resultados de diferentes métodos empíricos con la evapotranspiración estimada mediante el método estándar de la FAO-56 Penman-Monteith. La comparación del desempeño de los métodos se realizó mediante una evaluación cualitativa (graficas de dispersión) e indicadores estadísticos cuantitativos error porcentual (PE), raíz del error cuadrático medio (RMSE), índice de concordancia (d), coeficiente de correlación (r) e índice de confianza (c). Los resultados son alentadores para el método de HS_Berti pues estadísticamente tiene un desempeño optimo respecto a los demás métodos, con un RMSE =0.22mm/día, PE=3.24%, d=0.29, r=0.95 y c=0.27. Se concluye que el método de HS_Berti al tener el mejor desempeño, puede ser utilizado como una alternativa para la estimación de la ETo en casos de limitación de datos meteorológicos.

PALABRAS CLAVE: Cuenca Alto Apurímac, Hargreaves-Samani, Penman-Monteith, Ravazzani, Serruto, Turc

 

---

ABSTRACT

Reference evapotranspiration (ΕΤo) is a major component of the hydrological cycle and its estimation is essential for the net irrigation requirement, planning and management of regional water resources. The objective was to evaluate the performance of different empirical methods to estimate the reference evapotranspiration and propose an alternative to estimate the ETo in cases of limitation of meteorological data at the Yauri weather station. The methodology consisted of comparing the results of different empirical methods with the evapotranspiration estimated using the standard method of FAO-56 Penman-Monteith. The performance of the methods was compared using a qualitative evaluation (scatter plots) and quantitative statistical indicators percentage error (PE), root of the mean square error (RMSE), concordance index (d), correlation coefficient (r) and confidence index (c). The results are encouraging for the HS_Berti method because statistically it has an optimal performance with respect to the other methods, with an RMSE=0.22mm / day, PE=3.24%, d=0.29, r=0.95 and c=0.27. It is concluded that the HS_Berti method, having the best performance, can be used as an alternative for the estimation of ETo in cases of limited meteorological data.

KEYWORDS: High Apurímac basin, Hargreaves-Samani, Penman-Monteith, Ravazzani, Serruto, Turc

 

---

INTRODUCCIÓN

La evapotranspiración de referencia (ΕΤo) es un componente principal del ciclo hidrológico. Depende de las variables climáticas de temperatura, humedad, radiación solar y velocidad del viento (Allen et al., 1998; Jensen & Allen, 2016). Según Jensen & Allen (2016) la evapotranspiración es la suma de la vaporización mediante los procesos combinados de evaporación (E) y transpiración por las cuales se pierde el agua. La estimación confiable de ETo es esencial para estimar el requerimiento neto de riego, la planificación y la gestión de los recursos hídricos regionales y para modelar el efecto del cambio climático (Pandey et al., 2016). Un aumento de la evapotranspiración potencial en tiempo futuro, afectaría significativamente el balance dinámico del agua en una cuenca (Gharbia et al., 2018). En este sentido, cuantificar la evapotranspiración de referencia es importante.

La elección de un método depende de la disponibilidad de los datos meteorológicos, así como de la exactitud y precisión de las estimaciones del modelo para una determinada región (de Carvalho et al., 2013). La Organización para la Agricultura y la Alimentación (FAO) recomienda el uso del método de la FAO-56 Penman-Monteith para estimar la ETo (Allen et al., 1998); sin embargo, el método requiere gran cantidad de datos de entrada, que no siempre son accesibles (Chen et al., 2005; Berti et al., 2014; Lavado et al., 2015). Por lo tanto, para evitar aspectos como la limitación de datos, es necesario evaluar y seleccionar métodos alternativos que utilicen menos cantidad de datos meteorológicos; por ello diversos estudios se desarrollaron con el objetivo de evaluar el rendimiento de diferentes métodos de estimación de ETo, en base a comparaciones con el método estándar de la FAO-56 Penman-Monteith, entre ellos podemos citar a Treza (2008); Tabari (2010); Mohawesh (2011); da Cunha et al. (2013); Heydari et al. (2013); Mohammadi (2014); Lavado et al. (2015); Djaman et al., 2016; Dlugosz da Silva et al. (2017).

En este contexto, el objetivo del estudio fue evaluar el desempeño de diferentes métodos empíricos para estimar la evapotranspiración de referencia (ETo) y comparar los resultados con la evapotranspiración estimada mediante el método estándar de la FAO-56 Penman-Monteith en la estación meteorológica de Yauri.

MATERIALES Y MÉTODOS

Área de estudio y datos meteorológicos utilizados

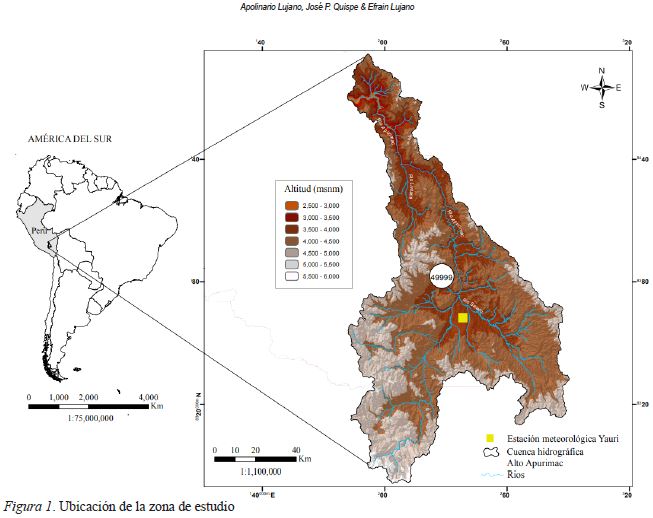
El estudio se realizó en la estación meteorológica de Yauri, ubicado en el distrito y provincia de Espinar, región Cusco e hidrográficamente en la cuenca Alto Apurímac (código 49999), ubicado en la latitud 14° 48’ 5" Sur, longitud 71° 25’ 54" Oeste y altitud de 3927 m.s.n.m. (figura 1). La zona de estudio es semiárida, y según el mapa de clasificación climática del Perú (SENAMHI), corresponde al clima C (o,i) C’ H2 (Zona de clima semi seco, frio, con deficiencia de lluvia en otoño e invierno, con humedad relativa calificada como seco). Mientras que la temperatura del aire y precipitación media anual son de 8 °C y 809,6 mm respectivamente.

Los datos meteorológicos utilizados corresponden al periodo 2000 - 2014 y fueron obtenidos del Servicio Nacional de Meteorología e Hidrología (SENAMHI). La información fue organizada en una hoja de cálculo Excel y los análisis se realizaron considerando los siguientes elementos meteorológicos: temperatura máxima (T_max, °C), temperatura mínima (T_min, °C), velocidad del viento (u₂, m/s), humedad relativa (HR, %) y horas sol (n, hr). Los cálculos se realizaron siguiendo las recomendaciones de Allen et al. (1998).

Ecuaciones de estimación de evapotranspiración de referencia

Se seleccionaron ecuaciones de evapotranspiración de referencia (ETo) basados en la simplicidad y en términos de cantidad de parámetros climáticos necesarios para resolverlos.

El método más preciso para estimar la ETo es mediante la aplicación de métodos que consideren todos los factores primarios que afectan la tasa de ETo, como la ecuación de Penman-Monteith (Jensen & Allen, 2016). La ecuación de la FAO-56 Penman-Monteith, se utilizó como método estándar global para estimar la evapotranspiración de referencia (ETo), considerado como el método más preciso, siendo la forma diaria de la ecuación según el manual de Riego y Drenaje N° 56 de la FAO de la siguiente manera (Allen et al., 1998):

Donde, ET₀ es la evapotranspiración de referencia (mm/día), Δ es la pendiente de la presión de vapor de saturación vs. curva de temperatura del aire (Kpa/C), Rn es la radiación neta en la superficie del cultivo (MJ/m²/d), G es el calor del suelo densidad de flujo en la superficie del suelo (MJ/m²/d), T es la temperatura media del aire (°C), u₂ es la velocidad del viento a 2 m de altura (m/s), e_s presión de vapor de saturación (kPa), e_a presión de vapor real (kPa), e_s - e_a déficit de presión de vapor de saturación (kPa), γ constante psicrométrica (kPa/°C).

Turc (1961), desarrolló una ecuación para las condiciones climáticas generales de Europa occidental. El método estimó la ETo basándose en mediciones de la temperatura máxima y mínima y la radiación solar utilizando las siguientes expresiones:

Donde, Rs es la radiación solar (MJ/m²/d), T_mean es la temperatura media del aire (°C), y λ es el calor latente de vaporización (MJ/Kg).

Hargreaves & Samani (1985), utilizado por su aplicación sencilla debido a que solo utiliza información de temperatura máxima y mínima, la ecuación se expresa como:

Donde, Ra es la radiación extraterrestre (mm/día) que depende de la latitud y el mes del año, T_mean, T_max y T_min, presentan el valor medio, máximo y mínimo de la temperatura del aire (°C).

Serruto (1993) propuso el siguiente modelo de estimación para el altiplano peruano, cuya expresión es: Donde, RS es la radiación solar extraterrestre (mm/día), es la temperatura media mensual (°C).

Droogers & Allen (2002), reportaron modificaciones de la ecuación de Hargreaves & Samani (1985), basado en las cuadrículas de datos del Atlas climático global del IWMI (International Water Management Institute), cuya ecuación es:

Donde, Ra es la radiación extraterrestre (mm/día) que depende de la latitud y el mes del año T_mean, T_max y T_min representan el valor medio, máximo y mínimo de la temperatura del aire (°C).

Ravazzani et al. (2012), investigaron la posibilidad de aplicar la ecuación de Hargreaves & Samani (1985) y propusieron un coeficiente basado en la altitud (Z) local en m. La expresión está dada por:

Donde, Ra es la radiación extraterrestre (mm/día) que depende de la latitud y el mes del año, T_mean, T_max y T_min representan el valor medio, máximo y mínimo de la temperatura del aire (°C).

Berti et al. (2014), modificaron los coeficientes empíricos de la ecuación original de Hargreaves & Samani (1985). La ecuación modificada se muestra a continuación:

Donde, Ra es la radiación extraterrestre (mm/día) que depende de la latitud y el mes del año, T_mean, T_max y T_min representan el valor medio, máximo y mínimo de la temperatura del aire (°C).

Evaluación estadística

Una primera verificación se realizó mediante el uso de gráficos y regresión lineal simple (pendiente, intercepto, R²). Según el análisis de regresión lineal simple, el mejor ajuste de un modelo se mide por la pendiente de la línea de regresión, el coeficiente de determinación cercanos a la unidad, y el intercepto cercano a cero (Vásquez-Méndez et al., 2011; da Cunha et al., 2013; Djaman et al., 2016).

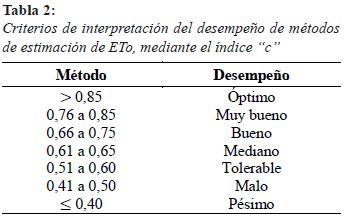
La evaluación del desempeño de los modelos, fue comparado con los valores de ETo obtenidos por los métodos empíricos, con el método preciso y estándar de la FAO-56 Penman-Monteith (Allen et al., 1998; Jensen & Allen, 2016); para ello se utilizaron las estadísticas de la raíz del error cuadrático medio (RSME), el error porcentual estimado (PE), el índice de concordancia (d) (Willmott, 1982) que varía entre 0 a 1 y representa cuánto los valores de ETo estimados por la forma estándar se ajustan a los valores obtenidos por los otros métodos empíricos, el valor de 1 indica una concordancia perfecta, mientras que, valores de 0 indican un mala concordancia (Willmott, 1982; Legates & McCabe, 1999). Para la validación de los métodos, se utilizó el coeficiente de correlación (r) y el índice de confianza (c), las ecuaciones se muestran en la tabla 1. El índice de confianza (c), se utilizó para clasificar la relación entre cada método con el método estándar, de acuerdo con la metodología propuesta por Camargo & Sentelhas (1997), según criterios de interpretación presentado en la tabla 2.

RESULTADOS Y DISCUSIÓN

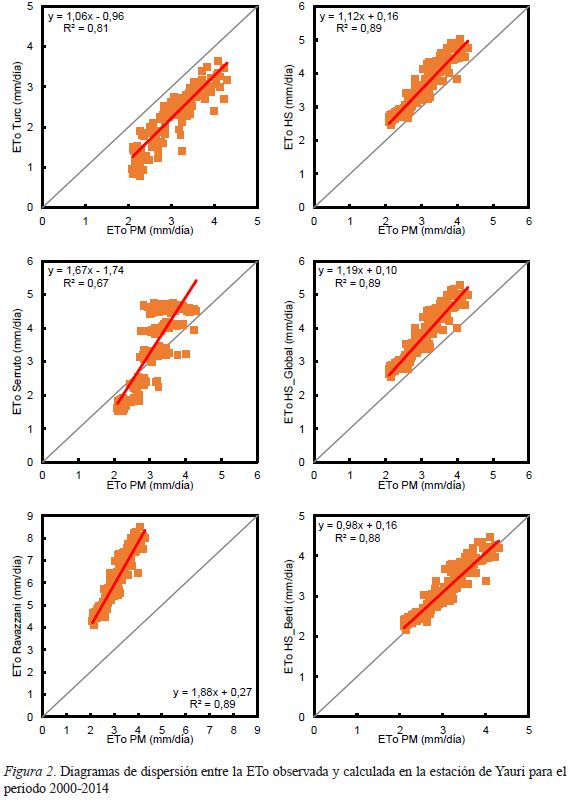
La relación entre las estimaciones de evapotranspiración de referencia (ETo) con la ecuación estándar de la FAO-56 Penman-Monteith (PM), se muestra en la figura 2. Los resultados presentaron coeficientes de determinación R2 que varían entre 0,67 a 0,89. Con respecto a las pendientes de las líneas de regresión de los métodos de Turc (Turc,1961), Hargreaves-Samani (HS) (Hargreaves & Samani, 1985), Serruto (Serruto, 1993), Hargreaves-Samani Global (HS_Global) (Droogers & Allen, 2002), Ravazzani (Ravazzani et al., 2012) y Hargreaves-Samani modificado (HS_Berti) (Berti et al., 2014) fueron de 1,06; 1,12; 1,67; 1,19; 1,88 y 0,98; mientras que los valores del intercepto resultaron ser de -0,96; 0,16; -1,74; 0,10; 0,27 y 0,16 respectivamente. Según los parámetros evaluados, el método de HS_Berti, podría ser una alternativa después de la ecuación de PM para la estimación de la ETo a condiciones locales de la estación de Yauri.

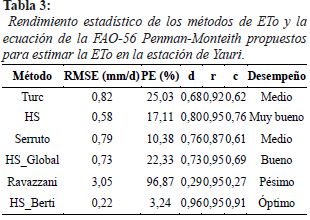
El rendimiento de los métodos de evapotranspiración de referencia en comparación con el método de la FAO-56 Penman-Monteith, basado en pruebas estadísticas, se muestra en la Tabla 3. El método de Turc subestimó la ETo, el RMSE tuvo un valor de 0,82 mm/día, y un PE de 25,03%. Mientras que el índice de concordancia (d), coeficiente de correlación (r) y el índice de confianza (c) resultaron con valores de 0,68; 0,92 y 0,62, con un desempeño mediano según las discreciones de Camargo & Sentelhas (1997). El método tuvo una alta correlación, sin embargo, no produjo resultados precisos de evapotranspiración de referencia. Los resultados del estudio coinciden con investigaciones realizadas por Lavado et al. (2015), que al comparar la ecuación de Turc con la ecuación de PM para las 8 estaciones ubicadas en la cuenca andina amazónica peruana, encontraron un valor (d) de 0,50 para la estación de Angostura, cercana a la zona de estudio.

El método de Serruto sobrestimó la evapotranspiración de referencia, tuvo un valor de RMSE de 0,79 mm/ día y PE de 10,38%. El índice de concordancia (d) y el coeficiente de correlación (r) tuvieron valores de 0,76 y 0,87 respectivamente, mientras el índice de confianza (c) alcanzó un valor de 0,61 con un desempeño mediano según los criterios de interpretación de Camargo & Sentelhas (1997). A pesar de que el método fue desarrollado para las condiciones del altiplano peruano, no estimó adecuadamente la evapotranspiración de referencia.

El método de Hargreaves & Samani (1985) y los métodos modificados Hargreaves-Samani Global de Droogers & Allen (2002), Ravazzani et al. (2012) y Hargreaves-Samani modificado de Berti et al. (2014), sobreestimaron la evapotranspiración de referencia bajo las condiciones de la zona de estudio. El método de Ravazzani demostró ser el peor entre los métodos evaluados, con un RMSE elevado de 3.05 mm/día, y un valor alto del error porcentual (PE) de 96,87% respectivamente, el índice de concordancia (d) fue de 0,29 el coeficiente de correlación (r) de 0,95 y el índice de confianza (c) solo alcanzó un valor bajo de 0,27 considerado como pésimo. Ravazzani et al. (2012) consideraron la altitud en la ecuación de Hargreaves- Samani para la estimación de la ETo, sin embargo, no tuvo un buen desempeño.

En cambio, los métodos de Hargreaves-Samani (Hargreaves & Samani, 1985) y Hargreaves-Samani Global (Droogers & Allen, 2002) tuvieron valores de RMSE de 0,58 y 0,73 mm/día, mientras que el PE para ambos métodos fue de 17,11 y 22,33%, el índice de concordancia (d) y el coeficiente de correlación (r) tuvieron valores de 0,95 para ambos métodos, con un índice de confianza (c) de 0,76 y 0,69 respectivamente, considerados como muy bueno y bueno. Los métodos evaluados tuvieron buena correlación, sin embargo, los resultados de estimación de la evapotranspiración de referencia no fueron precisos. Valores similares a nuestro estudio, para el método de Hargreaves-Samani, son reportados por Lavado et al. (2015) donde encontraron un coeficiente de correlación (r=0,98), índice de concordancia (d=0,91), mientras que el RMSE tuvo un valor de 0,45 mm/día, para la estación de Angostura.

Sin embargo, el método de Hargreaves-Samani modificado por Berti et al. (2014), mejoró el rendimiento para la zona de estudio en comparación entre los demás métodos evaluados, con un RMSE de 0,22 mm/día, PE de 3,24%, índice de concordancia (d=0,96), coeficiente de correlación (r=0,95), y el índice de confianza (c) alcanzó un valor de 0,91 con un desempeño óptimo, según los criterios de interpretación de Camargo & Sentelhas (1997). Empero de que el método fue modificado para la región de Veneto en Italia, estimó adecuadamente la evapotranspiración de referencia en la estación de Yauri.

La no adaptabilidad de los métodos de evapotranspiración de referencia propuestos por Turc (1961), Ravazzani et al. (2012), Serruto (1993) y Droogers & Allen (2002), podría haber resultado del desarrollo de estos modelos para una región climática específica (Djaman et al., 2015). Sin embargo, el método de HS_Berti (Berti et al., 2014) fue calibrado y validado para condiciones de la región de Veneto al noreste de Italia, y la aplicación de la misma ecuación en la zona de estudio, resulta válido, por presentar el mejor desempeño en la estimación de la ETo, después de la ecuación estándar de la FAO-56 Penman-Monteith, seguido por el método de Hargreaves-Samani.

CONCLUSIONES

El estudio evaluó el desempeño de seis métodos empíricos de evapotranspiración de referencia, en relación con el método estándar de la FAO-56 Penman-Monteith, bajo las condiciones de la estación meteorológica de Yauri. Los resultados muestran que el método de HS_Berti presentó un desempeño óptimo para la estimación de la ETo, seguido por el método de Hargreaves-Samani, HS_Global, Turc, Serruto y Ravazzani, que tuvieron desempeños de muy bueno, bueno, medio y pésimo, para la zona de estudio. El método de HS_Berti puede ser utilizado como una alternativa para la estimación de la ETo en caso de limitación de datos meteorológicos.

 

AGRADECIMIENTO

Los autores agradecen al Servicio Nacional de Meteorología e Hidrología del Perú (SENAMHI) por proporcionar la información utilizada en esta investigación. También expresan su gratitud a la Autoridad Nacional del Agua del Perú (ANA) por brindar su apoyo para el desarrollo de este estudio.

 

REFERENCIAS BIBLIOGRÁFICAS

Allen, R. G., Pereira, L. S., Rae, S. D., & Smith, M. (1998). Evapotranspiración del cultivo. Guías para la determinación de los requerimientos de agua de los cultivos. Roma: Estudio FAO, Riego y Drenaje Nº 56.         [ Links ]

Berti, A., Tardivo, G., Chiaudani, A., Rech, F., & Borin, M. (2014). Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agricultural Water Management, 140, 20-25. http://dx.doi.org/10.1016/j.agwat.2014.03.015         [ Links ]

Camargo, A. D., & Sentelhas, P. C. (1997). Avaliação do desempenho de diferentes métodos de estimativa da evapotranspiração potencial no Estado de São Paulo, Brasil. Revista Brasileira de agrometeorologia, 5(1), 89-97. Recuperado de http://www.leb.esalq.usp.br/agmfacil/artigos/artigos_sentelhas_1997/1997_RBAgro_5(1)_89-97_ETPM%E9todosSP.pdf         [ Links ]

Chen, D., Gao, G., Xu, C. Y., Guo, J., & Ren, G. (2005). Comparison of the Thornthwaite method and pan data with the standard Penman-Monteith estimates of reference evapotranspiration in China. Climate Research, 28(2), 123-132. Recuperado de https://www.int-res.com/articles/cr2002/cr2004/28/c028p123.pdf         [ Links ]

da Cunha, F. F., Magalhães, F. F., & de Castro, M. A. (2013). Métodos para estimativa da evapotranspiração de referência para Chapadão do Sul-MS. Revista Engenharia na Agricultura-Reveng, 21(2), 159-172. https://doi.org/10.13083/reveng.v21i2.346         [ Links ]

Djaman, K., Tabari, H., Balde, A. B., Diop, L., Futakuchi, K., & Irmak, S. (2016). Analyses, calibration and validation of evapotranspiration models to predict grass-reference evapotranspiration in the Senegal river delta. Journal of Hydrology: Regional Studies, 8, 82-94. https://doi.org/10.1016/j.ejrh.2016.06.003         [ Links ]

de Carvalho Alves, M., de Carvalho, L. G., Vianello, R. L., Sediyama, G. C., de Oliveira, M. S., & de Sá Junior, A. (2013). Geostatistical improvements of evapotranspiration spatial information using satellite land surface and weather stations data. Theoretical and applied climatology, 113(1-2), 155-174.         [ Links ]

Droogers, P., & Allen, R. G. (2002). Estimating reference evapotranspiration under inaccurate data conditions. Irrigation and drainage systems, 16(1), 33-45. Recuperado de https://www.futurewater.eu/wp-content/uploads/2013/01/PDroogers_2002_IrrigationDrainage.pdf         [ Links ]

Gharbia, S. S., Smullen, T., Gill, L., Johnston, P., & Pilla, F. (2018). Spatially distributed potential evapotranspiration modeling and climate projections. Science of The Total Environment, 633, 571–592. https://doi.org/10.1016/j.scitotenv.2018.03.208         [ Links ]

Hargreaves, G.H., & Samani, Z.A. (1985). Reference Crop Evapotranspiration from Temperature. Applied Engineering in Agriculture, 1, 96-99.         [ Links ]

Heydari, M. M., Abbasi, A., & Heydari, M. (2013). Estimation of evapotranspiration in Ardestan, Center of Iran. World Appl Sci J, 21(2), 230-236. DOI: 10.5829/idosi.wasj.2013.21.2.2511         [ Links ]

Jensen, M.E., & Allen, R.G. (2016). Evaporation, Evapotranspiration, and Irrigation Water Requirements, ASCE Manual and Reports on Engineering Practice, vol. 70. https://doi.org/10.1061/9780784414057         [ Links ]

Lavado, W., Lhomme, J., Labat, D., Loup Guyot, J., & Boulet, G. (2015). Estimación de la evapotranspiración de referencia (FAO Penman - Monteith) con limitados datos climáticos en la Cuenca Andina Amazónica Peruana. Revista Peruana Geo – Atmosférica, 4, 34-36. Recuperado de https://web2.senamhi.gob.pe/rpga/pdf/2015_vol04/paper3.pdf         [ Links ]

Legates, D. R., & McCabe Jr, G. J. (1999). Evaluating the use of "goodness‐of‐fit" measures in hydrologic and hydroclimatic model validation. Water resources research, 35(1), 233-241. https://doi.org/10.1029/1998WR900018         [ Links ]

Martins de Souza, J.; Rosa Pereira; L.; Matta Rafael, A. da; Dias da Silva, L.; Fialho dos Reis, E.; Bonomo, R. 2014. Comparison of methods for estimating reference evapotranspiration in two locations of Espirito Santo. Revista Brasileira de Agricultura Irrigada, 8(2), 114-126. DOI:10.7127/rbai.v8n200225         [ Links ]

Mohammadi, M. (2014). Comparison of Evapotranspiration Models for Estimating Reference Evapotranspiration in an Arid and Semiarid Region, Northeast of Iran. J. River Eng, 2(10), 34-41. Recuperado de http://hamkarfile.ir/up/2605.pdf         [ Links ]

Mohawesh, O.E. (2011). Evaluation of evapotranspiration models for estimating daily reference evapotranspiration in arid and semiarid environments. Plant Soil Environ., 57(4), 145–152. Recuperado de https://www.agriculturejournals.cz/publicFiles/240_2010-PSE.pdf         [ Links ]

Pandey, P. K., Dabral, P. P., & Pandey, V. (2016). Evaluation of reference evapotranspiration methods for the northeastern region of India. International Soil and Water Conservation Research, 4(1), 52-63. https://doi.org/10.1016/j.iswcr.2016.02.003         [ Links ]

Ravazzani, G., Corbari, C., Morella, S., Gianoli, P., & Mancini, M. (2011). Modified Hargreaves-Samani equation for the assessment of reference evapotranspiration in Alpine river basins. Journal of irrigation and drainage engineering, 138(7), 592-599.         [ Links ]

Serruto, R. (1993). Una nueva fórmula para el cálculo de la evapotranspiración potencial. Puno, Perú: PIWA.         [ Links ]

Tabari, H. (2010). Evaluation of reference crop evapotranspiration equations in various climates. Water Resources Management, 24(10), 2311–2337. https://doi.org/10.1007/s11269-009-9553-8         [ Links ]

Trezza, R. (2008). Estimación de evapotranspiración de referencia a nivel mensual en Venezuela: ¿Cuál método utilizar? Bioagro, 20(2), 89-95. Recuperado de http://ve.scielo.org/scielo.php?script=sci_arttext&pid=S1316-33612008000200002         [ Links ]

Vásquez-Méndez, Rebeca., Ventura-Ramos, Eusebio Jr., & Acosta-Gallegos, Jorge A. (2011). Habilidad de estimación de los métodos de evapotranspiración para una zona semiárida del centro de México. Revista mexicana de ciencias agrícolas, 2(3), 399-415. Recuperado de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S2007-09342011000300008         [ Links ]

Willmott, C. J. (1982). Some comments on the evaluation of model performance. Bulletin of the American Meteorological Society, 63(11), 1309-1313. https://doi.org/10.1175/1520-0477(1982)063<1309:SCOTEO>2.0.CO;2         [ Links ]

 

Artículo recibido: 04/01/2019

Artículo aceptado: 28/06/2019

En línea: 25/07/2019