Introducción
El consumo de energía basada en combustibles fósiles es perjudicial a través del efecto invernadero, el calentamiento global y la contaminación del aire (Martins et al., 2018). Se suman a este problema, el crecimiento poblacional, la carencia de recursos fósiles, y la reciente suba de precios del petróleo/gasolina (abril del 2022) en medio del conflicto en Ucrania (Gars et al., 2022; Neely, 2022). Estas, y otras razones impulsan al cambio general hacia las energías limpias con la utilización de recursos renovables (Adnan et al., 2021; Mohammadi et al., 2016). El sector rural de Laraqueri (ubicado al sur del Perú) no tiene acceso a la red eléctrica incluso hay islas en el lago Titicaca, que sufren del mismo problema, por lo tanto, es necesario dotar de alternativas de suministro de energía eléctrica. Se han efectuado varios trabajos previos utilizando la energía eólica en diferentes lugares incluido Perú (Alsamamra et al., 2022; He et al., 2022; Juanpera et al., 2021; Patidar et al., 2022; Tito et al., 2020, 2021) que tienen la finalidad de resolver este problema con la segunda mayor fuente de energía renovable, el viento.
Para dichos fines, la función de distribución de probabilidad de Weibull (WbPDF) tiene una alta eficiencia en el ajuste de los datos del viento y proporciona una predicción correcta del potencial de energía eólica de acuerdo con (Fazelpour et al., 2015) (Wais, 2017). El WbPDF se utilizó en estudios recientes para calcular los parámetros de la distribución con el fin de estimar el potencial de la energía eólica en diferentes regiones del mundo, como Chad, Turquía, Pakistán y Marruecos (Soulouknga et al., 2018) (Kaplan, 2018) (Khalid Saeed et al., 2019) (Shoaib et al., 2019) (Ouahabi et al., 2020).
Para estimar los parámetros de forma y escala de Weibull se pueden utilizar diferentes métodos que utiliza datos del viento. El método empírico fue sugerido por Justus et al. (C. ~G. Justus & Mikhail, 1976) (C. G. Justus et al., 1978), que se puede calcular utilizando el promedio y la desviación estándar de los datos de velocidad del viento, para proporcionar una solución práctica. El método del factor de patrón de energía fue presentado por Akdag y Dinler (Akdağ & Dinler, 2009), que supuestamente era adecuado para calcular la densidad de potencia y la velocidad promedio del viento.
Este estudio se caracteriza la disponibilidad del viento en Laraqueri para el año 2020, con la intención de viabilizar proyectos eólicos.
Materiales y métodos
Sitio de estudio y datos
El distrito de Laraqueri (Perú) está ubicado en el departamento de Puno, provincia de Puno y distrito de Pichacani. Latitud sur: 16°8'9.3'', longitud oeste: 70°2'45.2'' y altitud: 3928 m s. n. m.
Los datos meteorológicos se obtuvieron del SENAMHI (Servicio Nacional de Meteorología e Hidrología del Perú, 2022) para los años de estudio 2000-2021 y de la Administración Nacional de Aeronáutica y el Espacio (National Aeronautics and Space Administration, 2022) datos de toda la serie de tiempo disponible para el lugar de estudio, es decir, de enero del 2001 hasta diciembre del 2021.
Para analizar y optimizar los sitios de viento, se requiere información sobre el viento, pero no se pueden predecir con precisión variables caóticas como la dirección y la velocidad del viento. Tales variables a menudo se estudian utilizando herramientas estadísticas. Estas características se analizan en las siguientes secciones.
Donde: νpromedio- velocidad media o promedio; σ - desviación estándar; I t - intensidad de turbulencia.
Función de distribución de Weibull
La función de distribución de datos más utilizada para el viento es la distribución de Weibull, debido a la mejor descripción que proporciona en el caso de los datos del viento, en comparación con las otras funciones de distribución. Hay dos variaciones de la función Weibull dependiendo del número de parámetros utilizados. Para los datos del viento, se utilizan principalmente dos parámetros, si v es la velocidad del viento (m/s), entonces la función distribución de probabilidad (PDF) de Weibull f(v), se expresa como (Saleh et al., 2012):
Donde, c (m/s)- es la escala y k - la forma. El área bajo la curva de la función de densidad de probabilidad se llama función de distribución acumulativa. Entonces, la función de distribución acumulativa (CDF) de Weibull se puede lograr tomando una integral de f (v), denotada por F(v) y dada como:
Métodos para estimar los parámetros de Weibull c y k
Existen muchos métodos numéricos para calcular los parámetros de Weibull. En este estudio se comparan dos técnicas.
Método empírico de Justus (EMJ)
Los parámetros k y c se pueden calcular mediante las fórmulas (6) y (7) (C. ~G. Justus & Mikhail, 1976).
Donde v promedio es la velocidad promedio, Γ es la función gamma
Método de densidad de potencia.
Los parámetros k y c se pueden calcular mediante las fórmulas (Shoaib et al., 2019) (Akdağ & Dinler, 2009)
Donde: Fe - factor de patrón de energía
Para estimar la frecuencia acumulada de las velocidades que son mayores o iguales a un cierto valor V, se usó la distribución acumulada complementaria F' (López, 2012).
Estimación de indicadores de viento
La densidad de potencia eólica (Pw/A) es el indicador más significativo para el viento que describe la cantidad de energía producida por diferentes velocidades del viento en un sitio seleccionado. Tanto los datos reales de la velocidad del viento medidos en un sitio como el análisis de distribución de Weibull se pueden usar para calcular la Pw/A del viento. Las fórmulas se dan como (Keyhani et al., 2010) (Khahro et al., 2014):
El viento Pw/A (W/m2) se define como la potencia en el viento (Pw) dividida por el área barrida de la turbina (A). Aquí ρ es la densidad de aire estándar, considerada principalmente como constante de 1.225 kg/m3 a nivel del mar (1 atm) y 15° C.
Para estimar la densidad del aire(ρ) puede determinarse de forma indirecta conociendo la temperatura, altura sobre el nivel del mar:
Donde 𝜌 - densidad del aire, h - altitud sobre el nivel del mar del lugar alto andino de estudio y T- temperatura del lugar.
Variación de la potencia con la altura
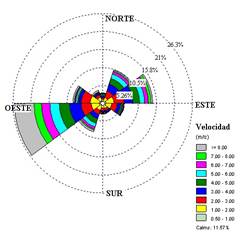
Rosa de los vientos
El diagrama de la rosa de los vientos es una herramienta que muestra gráficamente la velocidad y la dirección del viento en una ubicación particular durante un período de tiempo.
Análisis estadístico para la bondad de ajuste de la función del modelo
Prueba de Chi-cuadrado
Conocido también como Ji-cuadrado, esta prueba contrasta frecuencias observadas con las frecuencias esperadas, y tiene la siguiente fórmula cálculo:
donde Oi representa a cada frecuencia observada y Ei representa a cada frecuencia esperada.
Coeficiente de correlación de Pearson R
El coeficiente de correlación de Pearson es una medida de dependencia lineal entre dos variables aleatorias cuantitativas. El coeficiente de correlación de Pearson cuando es aplicado a una muestra se suele denotar por R:
Donde, n es el tamaño de la muestra, x
i
, y
i
son puntos muestrales individuales indexados con i. Finalmente,
Coeficiente de determinación R2
Refleja la bondad del ajuste de un modelo a la variable que pretender explicar. Su valor oscila entre 0 y 1, cuanto más cerca de 1 se sitúe su valor, mayor será el ajuste del modelo a la variable que se intenta explicar, de forma inversa, cuanto más cerca de cero, menos ajustado estará el modelo.
Resultados y discusión
En la figura 1 se muestra los promedios de velocidad del viento (m/s) según meses y la regresión lineal correspondiente y donde se aprecia una tendencia a ser constante respecto a la velocidad del viento.
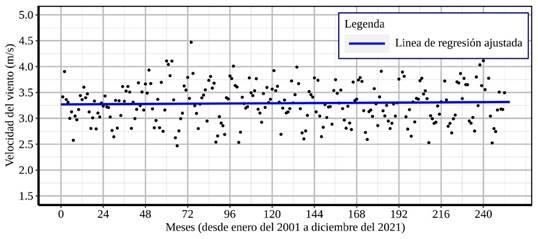
Figura 1 Promedios mensuales de las velocidades del viento (m/s) según meses (enero 2001 a diciembre 2020) y la regresión lineal correspondiente
Se realizó un análisis estadístico, específicamente el análisis de regresión lineal, utilizando el Software Estadístico R sobre los datos de velocidad del viento para describir las características del sitio de estudio. Con la finalidad de revisar la tendencia, se empleó los datos descargados de la NASA (https://power.larc.nasa.gov/data-acceso-espectador), esto debido a los años que abarca. En la figura 1 se muestra los promedios de las velocidades del viento según meses (de 21 años desde enero del 2001 hasta diciembre del 2021), es decir, en la figura indicada el eje de las abscisas (horizontal): 0 es enero de 2001, 1 es febrero de 2001, 2 es marzo de 2001, así sucesivamente hasta llegar a diciembre del 2021; en dicho gráfico se muestra también la regresión lineal correspondiente. Se puede observar que el viento promedio es prácticamente constante a lo largo de los 21 años, los resultados de la regresión muestran una pendiente reducida de 0.0001804652, el cual es próximo a cero (considerando que la pendiente es susceptible a datos atípicos).
Tabla 1 Los valores de los parámetros de Weibull para el año 2020.
| Meses | v prom | σ | σ vprom | Método empírico (Justus) | Método de densidad de potencia | ||||
|---|---|---|---|---|---|---|---|---|---|
| k | c | Pw /A (W/m2) | k | c | Pw /A (W/m2) | ||||
| Enero | 3.55 | 2.82 | 0.79 | 1.28 | 3.83 | 62.00 | 1.32 | 3.90 | 60.69 |
| Febrero | 2.98 | 2.38 | 0.80 | 1.28 | 3.21 | 36.90 | 1.33 | 3.28 | 35.78 |
| Marzo | 2.82 | 2.22 | 0.79 | 1.30 | 3.05 | 30.43 | 1.33 | 3.10 | 29.95 |
| Abril | 3.03 | 2.35 | 0.78 | 1.32 | 3.29 | 36.70 | 1.33 | 3.32 | 36.69 |
| Mayo | 3.33 | 2.82 | 0.85 | 1.20 | 3.54 | 58.44 | 1.25 | 3.61 | 55.70 |
| Junio | 3.60 | 3.00 | 0.83 | 1.22 | 3.85 | 71.25 | 1.28 | 3.93 | 67.80 |
| Julio | 3.07 | 2.48 | 0.81 | 1.26 | 3.30 | 41.42 | 1.30 | 3.36 | 40.48 |
| Agosto | 4.47 | 3.55 | 0.79 | 1.28 | 4.83 | 123.40 | 1.34 | 4.94 | 119.24 |
| Setiembre | 3.50 | 2.66 | 0.76 | 1.34 | 3.81 | 54.55 | 1.37 | 3.85 | 54.39 |
| Octubre | 3.36 | 2.76 | 0.82 | 1.24 | 3.60 | 56.31 | 1.29 | 3.68 | 54.19 |
| Noviembre | 4.49 | 3.24 | 0.72 | 1.43 | 4.94 | 104.71 | 1.45 | 4.99 | 104.88 |
| Diciembre | 3.85 | 2.79 | 0.73 | 1.42 | 4.23 | 66.55 | 1.44 | 4.26 | 66.06 |
| Promedios | 3.50 | 2.76 | 0.79 | 1.30 | 3.79 | 61.89 | 1.33 | 3.85 | 60.49 |
También, se obtuvo un coeficiente de intercepto de 3.269264, luego la función de regresión lineal estaría dada por Velocidad = 3.269264 + 0.0001804652*Mes.
En la tabla 1 se muestran los resultados, la velocidad promedio por meses, la desviación estándar, la intensidad de la turbulencia y los parámetros de la función de Weibull con los métodos empírico y método de densidad de potencia; la velocidad media es de 3.5 m/s (anual). En la tabla 1 se tiene una potencia de 61.89 (W/m2) el cual es bajo según (Manwell et al., 2010), por lo tanto, no es recomendable para turbinas rápidas, pero si puede ser usado para turbinas de eje vertical de extracción de agua. En la tabla 1 se muestran los valores de la densidad de potencia a 10 metros con c, k obtenidos por método de densidad de potencia; registrándose un valor máximo de 119.24 W/m2 en agosto y 123.40 W/m2 con el método empírico.
En la tabla 1 se aprecian los valores de los parámetros de Weibull analizados con los métodos empírico y método de densidad de potencia, las velocidades medias mensuales (v), desviación estándar (σ), intensidad de turbulencia ( σ/v promedio), densidad de potencia (P w /A). El valor de "c" (escala) alcanza un máximo de 4.94 m/s en noviembre y 4.83 en agosto y un mínimo de 3.05 m/s en marzo.
La tabla 2 muestra probabilidades y bondad de ajuste por mes. El mes con mayor probabilidad de tener vientos con velocidad mayor o igual a 3 es agosto y noviembre, con una probabilidad de 0.58 y 0.61 respectivamente, y en general, la probabilidad media anual es Pr = 0.47 y 0.48 prácticamente igual en ambos métodos.
Tabla 2 Probabilidad de viento mayor o igual a 4 m/s y prueba de bondad de ajuste de la distribución Weibull por meses
| Meses | Método empírico | Método de densidad de potencia | ||||||
|---|---|---|---|---|---|---|---|---|
| Pr(v ≥ 3) | χ 2 | R | R 2 | Pr(v ≥ 3) | χ 2 | R | R 2 | |
| Enero | 0.48 | 0.01 | 0.99 | 0.98 | 0.49 | 0.01 | 0.98 | 0.97 |
| Febrero | 0.4 | 0.03 | 0.97 | 0.94 | 0.41 | 0.04 | 0.96 | 0.91 |
| Marzo | 0.38 | 0.03 | 0.99 | 0.97 | 0.38 | 0.03 | 0.98 | 0.97 |
| Abril | 0.41 | 0.04 | 0.99 | 0.98 | 0.42 | 0.04 | 0.99 | 0.98 |
| Mayo | 0.44 | 0.03 | 0.97 | 0.95 | 0.45 | 0.04 | 0.97 | 0.93 |
| Junio | 0.48 | 0.04 | 0.98 | 0.95 | 0.49 | 0.05 | 0.96 | 0.93 |
| Julio | 0.41 | 0.03 | 0.96 | 0.93 | 0.42 | 0.04 | 0.96 | 0.92 |
| Agosto | 0.58 | 0.02 | 0.98 | 0.95 | 0.6 | 0.02 | 0.97 | 0.93 |
| Setiembre | 0.48 | 0.02 | 0.98 | 0.97 | 0.49 | 0.02 | 0.98 | 0.96 |
| Octubre | 0.45 | 0.03 | 0.98 | 0.96 | 0.46 | 0.04 | 0.97 | 0.94 |
| Noviembre | 0.61 | 0.01 | 0.99 | 0.99 | 0.62 | 0.01 | 0.99 | 0.98 |
| Diciembre | 0.54 | 0.04 | 0.96 | 0.92 | 0.55 | 0.04 | 0.96 | 0.91 |
| Promedios | 0.47 | 0.03 | 0.98 | 0.96 | 0.48 | 0.03 | 0.97 | 0.95 |
La calidad de la curva ajustada depende de la precisión de los parámetros (c, k) de la función de Weibull. Se consideraron dos métodos en la determinación de los factores de Weibull para los datos de cada mes, el análisis estadístico se realizó utilizando el Chi-cuadrado (χ2) y el coeficiente de correlación de Pearson (R). En la tabla 2 se muestran los resultados de los métodos, los ajustes dependen de los meses, hay meses que se ajustan más y otros no, esto debido a la variabilidad de los vientos, por lo que también creemos conveniente obtener resultados por meses. Sin embargo, si se consideran los promedios, entonces el método empírico es ligeramente el mejor método para determinar la función de distribución de Weibull (tiene un valor de χ2 = 0.03 y un mejor coeficiente de correlación de Pearson R = 0.98).
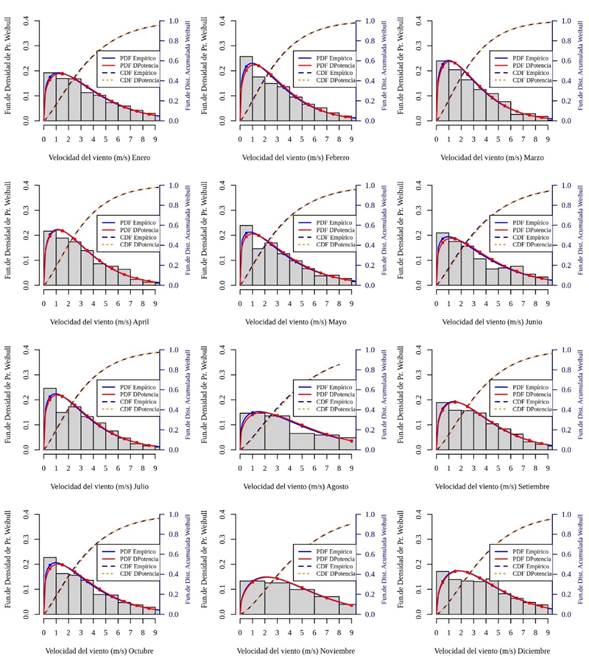
Figura 2 Comparación entre las funciones teóricas de densidad de probabilidad de Weibull y los histogramas de velocidad del viento observados de los meses y la función de distribución acumulativa de Weibull (líneas discontinuas y puntos)
La figura 2 compara las funciones teóricas de densidad de probabilidad con el histograma de la velocidad del viento, se observan vientos más altos en los meses de agosto a diciembre que en el resto de los meses. Cada figura correspondiente a un mes muestra el ajuste de la curva f(v) de la función de densidad de probabilidad de Weibull y el histograma de los datos observados, con el fin de identificar fácilmente qué mes tiene el mayor potencial eólico. En todos los meses, los datos observados y calculados están estrechamente relacionados entre sí.
Para la obtención de la densidad de potencia disponible en el viento (WPD) se consideró una densidad del aire promedio en ρ=0.79Kg/m 3 este valor depende de la altitud en la que se encuentra la ciudad
Los datos registrados por la temperatura y presión de la estación meteorológica del SENAMHI: Tpromedio = 7° C, la altura en metros sobre el nivel del mar: h = 3 928 m s. n. m. Entonces, la densidad se calcula con la siguiente fórmula:
La tabla 3 muestra un aumento de la densidad de potencia con la altura, y a 80 metros tiene un valor de 150.89 W/m2.
Tabla 3 Variación de la densidad de potencia con la altura
| Altura (m) | Pw/A (W/m2) |
|---|---|
| 10.00 | 61.89 |
| 20.00 | 83.30 |
| 30.00 | 99.11 |
| 40.00 | 112.11 |
| 50.00 | 123.36 |
| 60.00 | 133.39 |
| 70.00 | 142.50 |
| 80.00 | 150.89 |
| 90.00 | 158.70 |
La velocidad promedio es de 3.5 m/s en Laraqueri y una densidad de energía eólica de 61.89 W/m2. Estos valores se corroboran con el atlas eólico peruano (Vidal, 2008).
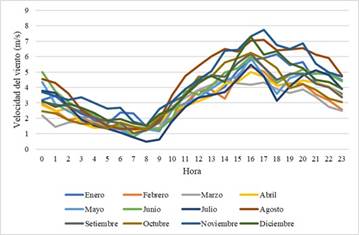
Figura 3 Velocidad del viento para la ciudad de Laraqueri a 10 m. de altitud durante todas las horas del día para todos los meses del año 2020
La figura 3 muestra que hay más intensidad de viento entre las 15 y las 19 horas (en un día), considerando una altura de 10 m. y todas las horas del año (2020).
Conclusiones
En el presente estudio se encontró que la velocidad media mensual del viento en Laraqueri es relativamente baja, con una velocidad media anual de 3.5 m/s. De agosto a diciembre, la velocidad del viento muestra una mayor velocidad con relación a los demás meses. Los resultados obtenidos fueron validados y se encontraron buenos ajustes para las curvas de la función de densidad de probabilidad de Weibull aplicadas a los datos observados. Para ello, se utilizaron pruebas estadísticas para cada mes y para cada método considerado con resultados muy similares.
El factor de forma de la distribución de Weibull (k) es 1.2 en mayo. Es un valor menor a 2 lo que indica que la gráfica de la distribución de Weibull es asimétrica, el factor de escala (c) tiene un valor cercano a la velocidad promedio.
La densidad de potencia eólico calculado en Laraqueri tiene un valor de promedio de 61.89 W/m2, que es un valor pequeño. Los vientos en la ciudad de Laraqueri son aptos para turbinas de baja potencia y preferiblemente verticales. La velocidad que supera los 3 m/s es de 47 % en promedio durante el año, esto significa que los aerogeneradores de baja potencia funcionarían aproximadamente casi medio año.
Se observa que la velocidad del viento no es constante y las direcciones de estas varían, existiendo una dirección dominante en torno a los 266°.












 uBio
uBio