INTRODUCCIÓN
There are diverse cases or real situations in which we have to consider several variables simultaneously. Thus, it is possible to think and propose problems in all disciplines in which we record data of more than one variable on different elements or individuals of a sample. For instance, animal nutrition and feeding studies are usually conducted to determine the nutritional composition and content of anti-nutrients, as in sacha inchi (super seed) Plukenetia volubilis and Plukenetia huayllabambana, for which the variables of moisture content, crude protein, crude fiber, ethereal extract, nitrogen free extract, ash, among others, are analyzed (Taipe Cuadra et al., 2022).
In plant physiology, research has been conducted on the chemical and fermentative characteristics, in vitro, of Moringa oleifera pod and leaf, evaluating variables such as dry matter, crude protein, detergent fiber, among others (Sánchez-Santillán et al., 2022). Likewise, in the field of transformation and agroindustry, research has been undertaken on the chemical characterization of the species Rosa x grandif lora Hort., Helianthus annuus L., and Calendula officinalis L., to determine the nitrogen and carbohydrate content of their components (de Lima Franzen et al., 2019). In fact, each of the studies presents evidence of univariate statistical analysis.
In many cases it is appropriate to study each of the variables of interest individually (Bhunia et al., 2023). However, in general, multiple variables are related to each other; thereby, individual analyses provide limited information about the structure of the data set (Todorov et al., 2020). Hence, multivariate analysis techniques include both purely descriptive methods that aim to extract information from the available data, and inferential methods that, through the construction of models, seek to draw conclusions about the population that generated the data.
In addition, multivariate analyses are valid to test the hypothesis where the means of the variables analyzed have a specific value (inference on the mean in multivariate populations) (Mejía-Trejo, 2017), to represent the information by means of a smaller number of variables constructed as linear combinations of the original ones and that explain most of the original variability (Principal Component Analysis) (Pearson, 1901), to find a model that allows us to predict a group of variables of the original set from another group of variables (Multivariate Regression Models) (Alexopoulos, 2010) and to compare the vector means of the response variables with one or more factors (Multivariate Analysis of Variance) (Finch, 2022).
Under this scope, statistics has become an important tool and essential in many areas of scientific life (Gupta et al., 2018; Wang et al., 2022). In spite of this, many articles rejected in scientific journals in the agronomic field and other related fields, are due to a wrong approach of the experiments or a not correct statistical analysis of the data, in many cases as a result of a deficiency of understanding of rigorous methods (Fernández Escobar et al., 2018).
Here, multivariate analysis is a rigorous statistical technique, which calculation is matrix-based (Cuadras, 2014). The application of multivariate analysis of variance (MANOVA), for completely randomized designs, is an appropriate technique to study the association between two sets of variables, such as one or more factors and their effect on more than one characteristic or response variable.
In this context, the present research aims to evaluate the multivariate effect of an organic and inorganic fertilizers mixture on the growth of Lactuca sativa L.
METHODS
Research design
The investigation was conducted using the multivariate method in a completely randomized design (Sánchez Sellero, 2009), with a factor composed of an organic and inorganic fertilizers mixture for 4 levels or treatments, as follows: T1 = guinea pig manure - urea 250 g/parcel, T2 = guinea pig manure - diammonium phosphate 250 g/parcel, T3 = compost - urea 250 g/parcel, and T4 = compost - diammonium phosphate 250 g/parcel; each with 5 replicas. The ratio of organic to inorganic fertilizer mixtures was 1:1 w/w. In order to evaluate the effect of the treatments on the growth of L. sativa L., we determined the number of leaves (Y2) and plant height (Y1).
The multivariate effect in a randomized design can be expressed as a linear model (Sánchez Sellero, 2009), which formula is as follows:
yig = µ + αi + εig (1)
i=1,2, 3, …, t ; g=1,2, 3, …, k
Where yig is the multivariate response variable or observed random vector, affected by the level i of the organic and inorganic fertilizer mixture in the experimental unit g, μ is a vector of general averages, αi is the effect of level i of the organic and inorganic fertilizer mixture, and εig is a vector of experimental errors due to the effect of the level i of the organic and inorganic fertilizer mixture, in the multivariate experimental unit g of the observable variables.
Population and data collection
The population consisted of lettuce of the variety L. sativa L. in the experimental parcels. Seeds of L. sativa L. were provided by Escuela Profesional de Ingeniería Agrónoma of the Universidad Nacional del Santa. The parcels constitute the experimental units and the lettuce plants constitute the observation units. They do not always coincide (Kuehl, 2000).
The sample consisted of 20 experimental parcels; 1 m wide by 2 m long (area = 2 m2). In each experimental parcel, 6 lettuces were planted, using randomly selected seeds of the variety under study. For analysis purposes, 3 of the 6 plants were used to measure the response variables. The experiment included 5 replicates for each of the 4 treatments. Measurements and counting were performed in each experimental parcel at the time of harvest (after 80 days), which values were recorded on a spreadsheet according to the randomized experimental scheme (Figure 1).
The number of leaves of each plant observed was determined by simple counting of 3 lettuce plants, while the height of each plant was determined in centimeters (cm) with a ruler. Furthermore, all methods were carried out in accordance with relevant guidelines. No exotic species were introduced into the country during this experiment.
Statistical analysis
Data processing was performed using SPSS v26.0 software, reporting descriptive measures for each response variable by treatment, including arith-metic mean and standard deviation. Multivariate analysis was performed on the basis of the general linear model, including multivariate and univariate tests. The multivariate statistics to evaluate the effect of the factor were: Pillai’s trace, Wilks’ Lambda, Hotelling trace and Roy’s Largest Root. The univariate tests were analysis of variance for treatments using the F-test and Tukey multiple comparisons tests. The model adequacy test was tested by multivariate normality and homogeneity of the errors from the residuals. The Doornik-Hansen test, performed in Stata software v15.1 (Stata Corp, 2017), was used for multivariate normality, and Box’s M test for equality of covariance matrices. The significance level was considered at 5%.
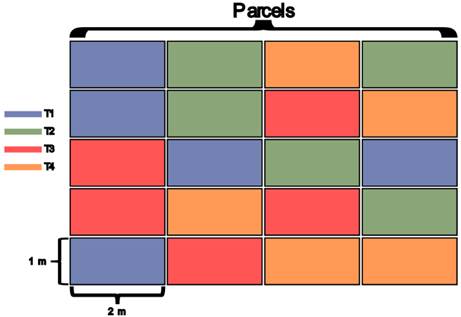
Figura 1 Randomized experimental scheme for data recording. Each square represents an experimental unit (parcel) and each color represents an experimental treatment. T1 (blue square) with guinea pig manure - urea at 250 g/parcel, T2 (green) with guinea pig manure - diammonium phosphate at 250 g/parcel, T3 (red) with compost - urea at 250 g/parcel, and T4 (orange) with compost - diammonium phosphate at 250 g/parcel; all with 5 replicas.
RESULTS Y DISCUSSION
Statistics has become a fundamental tool for all areas of knowledge (Diggle, 2015; Gupta et al., 2018; Jalajakshi & Myna, 2022; Weihs & Ickstadt, 2018), especially in agriculture (Bender, 2020), however, it needs to be rigorously applied to avoid misinterpretation or confusion. In our research, we employed a multivariate analysis to evaluate the effect of the variables number of leaves and height of L. sativa L., a widely cultivated vegetable and on which several studies have been conducted on its cultivation (Muscolo et al., 2022; Travieso et al., 2016), physiology (Tang et al., 2015; Zhao et al., 2022) and hydroponics (Jung & Kim, 2020; Lei & Engeseth, 2021).
Table 1 displays the growth of L. sativa L. in relation to the number of leaves. It was found that the treatment compost - diammonium phosphate (T4) had the highest average of 21,2 ± 1,483 leaves, and the lowest average was for guinea pig manure - diammonium phosphate (T2) with 15,00 ± 2,345 leaves.
Table 1 L. sativa L. growth with different organic and inorganic fertilizers mixtures
| Response variable and treatments | Mean | SD |
|---|---|---|
| Number of lettuce leaves | ||
| T1 = guinea pig manure - urea | 19,00 | 0,707 |
| T2 = guinea pig manure - diammonium phosphate | 15,00 | 2,345 |
| T3 = compost - urea | 18,00 | 1,000 |
| T4 = compost - diammonium phosphate | 21,20 | 1,483 |
| Lettuce height (cm) | ||
| T1 = guinea pig manure - urea | 7,358 | 0,431 |
| T2 = guinea pig manure - diammonium phosphate | 6,452 | 0,310 |
| T3 = compost - urea | 7,722 | 1,058 |
| T4 = compost - diammonium phosphate | 10,018 | 0,666 |
Nota: SD = standard deviation.
In regard to height, the compost - diammonium phosphate treatment (T4) showed the highest average of 10,018 ± 0,666 cm and the lowest average was obtained by the guinea pig manure - diammonium phosphate (T2) with 6,452 ± 0,310 cm. The comparison of means of the number of leaves and plant height by the effect of each of the treatments is formalized later.
On the other hand, when establishing the Pearson correlation between the dependent variables number of leaves and plant height, R = 0,650, t(1;18) = 3,629, p = 0,002 was obtained, evidencing a strong positive and significant relationship. Therefore, it is justified the multivariate analysis of variance (MANOVA), presented in Table 2.
Table 2 Multivariate effect analysis of organic and inorganic fertilizer mixtures on L. sativa L. growth
| Satistical test | Value | F | P |
| Pillai’s Trace | 1,112 | 6,682 | <0,00 |
| Wilks’ Lambda | 0,078 | 12,918 | <0,00 |
| Hotelling Trace | 9,400 | 21,934 | <0,00 |
| Roy’s Largest Root | 9,133 | 48,710 | <0,00 |
Indeed, the multivariate analysis of variance showed that each of the Pillai’s Trace, Wilks’ Lambda, Hotelling Trace, and Roy’s Largest Root statistical tests demonstrated that there is a significant effect of the organic and inorganic fertilizer mixtures treatments on the average number of leaves and average height of L. sativa L., at the 0.05 level, we obtained F(6;32) = 6,682, p = 0,000, F(6;30) = 12,918, p = 0,000, F(6;28) = 21,934, p = 0,000 and F(3;16) = 48,710, p = 0,000, respectively. Univariate analysis was then performed as shown in Table 3 with respect to the effect of treatments on each of the response variables.
In this regard, it is evident that the organic and inorganic fertilizer mixtures had a significant influence on the average number of leaves and the average height of L. sativa L., since at the 0,05 level we obtained F(3;6) = 14,406, F(3;6) = 24,957, p < 0,05, respectively. This result leads to perform the multiple comparisons test, presented in Figure 2, in order to determine which treatments affected the experiment.
Table 3 Multivariate effect analysis of organic and inorganic fertilizer mixtures on L. sativa L. growth.
| Variation source | DV | Sum of squares | F | P |
| Treatments | Number of leaves | 99,400 | 14,406 | <0,00 |
| Height | 34,537 | 24,957 | <0,00 | |
| Error | Number of leaves | 36,800 | --- | --- |
| Height | 7,381 | --- | --- | |
| Total | Number of leaves | 136,200 | --- | --- |
| Height | 41,918 | --- | --- |
Nota: DP = dependent variable.
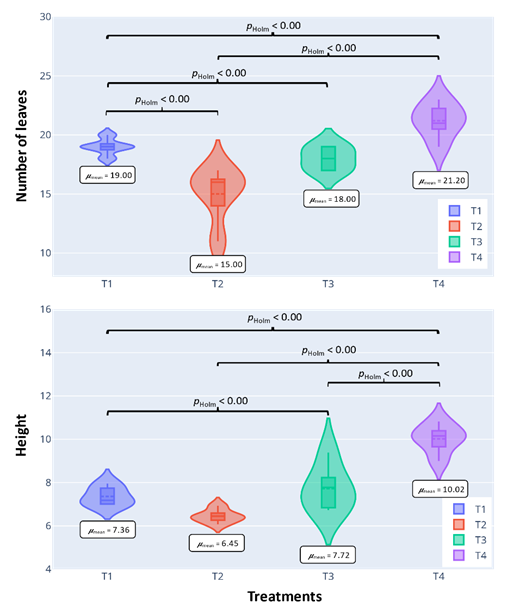
Figure 2 Data distribution and comparison of the effect of the organic and inorganic fertilizer mixtures on L. sativa L. growth, according to Tukey’s univariate test. It is displayed the statistical difference (p <0.05) in the number of leaves and heigh for each experimental treatment.
Consequently, Tukey’s multiple comparisons test was performed and as a result it was determined that there is a significant difference in the average number of leaves between the treatments guinea pig manure - diammonium phosphate with compost-urea, guinea pig manure - urea and compost - diammonium phosphate, as well as compost - urea with compost - diammonium phosphate.
This evidenced that the guinea pig manure - diammonium phosphate treatment generated the lowest average number of leaves (15,00) and the compost - diammonium phosphate treatment generated the highest average number of leaves (21,20). There were also significant differences in the average height of L. sativa L., between the treatment’s guinea pig manure - diammonium phosphate with compost - urea and compost - diammonium phosphate, as well as significant differences between compost - urea and compost - diammonium phosphate. Consequently, the guinea pig manure - diammonium phosphate treatment generated the lowest average height (6,452 cm) and the compost - diammonium phosphate treatment generated the highest average height (10,018 cm). Therefore, the results found with the proposed multivariate model are reliable if the assumptions of the residues are verified (Table 4).
To this regard, the test for normality and multivariate homoscedasticity of the residuals determined a p = 0,244 > 0,05 and p = 0,180 > 0,05, respectively. Consequently, it has been significantly demonstrated that there is multivariate normality as well as multivariate homoscedasticity of the residuals (Table 4). Thus, it is assumed that there is sufficient evidence to support the adequacy of the model.
Table 4 Analysis of the adequacy of the multivariate model of the effect of organic and inorganic fertilizer mixtures on L. sativa L. growth
| Multivariate normality test of the residuals | Chi-square | 2,818 |
| P | 0,244 | |
| Box’s test for equality of covariance matrices | Box’s M test | 16,402 |
| F | 1,406 | |
| p | 0,180 |
It should be highlighted that L. sativa L. is a species of great interest due to the fact that a significant number of people are changing their alimentary habits towards a healthier life, incorporating it in their diet (Kim et al., 2016; Ocean et al., 2019). For this reason, conducting experiments and relevant statistical analysis will provide a deeper knowledge to explain the study variables inherent to its cultivation, which ultimately ends up benefiting producers.
In our experiment, the growth of L. sativa L., in relation to the number of leaves, showed that the treatment composed by the mixture compost - diammonium phosphate presented the highest average of 21,2 ± 1,483 and the lowest average was presented by the guinea pig manure - diammonium phosphate with 15,00 ± 2,345. In terms of height, the treatment composed by compost - diammonium phosphate mixture showed the highest average of 10,02 ± 0,666 cm and the lowest average was obtained with guinea pig manure - diammonium phosphate with 6,452 ± 0,310 cm.
In contrast to other study, where the growth of L. sativa L. was also evaluated, an average number of leaves of 26,7 and an average height of 21,9 cm were determined, despite being subjected to stress conditions; in addition, plants were reported with a lower number of leaves and height, 13,2 and 4,5 cm, respectively (Yavuz et al., 2023). Here, we note that our values for number of leaves and height are lower, however, we must recognize that the growing conditions are variable in each region, and there may be environmental and intrinsic effects of the species that generate variation in our findings. Despite this, we emphasize the statistical differences found between treatments, especially between T2 and T4.
To justify the multivariate analysis of variance, the Pearson correlation between the dependent variables number of leaves and plant height was evaluated, resulting in R = 0,650, t(1;18) = 3,629, p = 0,002, showing a strong positive and significant relationship. Indeed, the multivariate analysis of variance showed that each of the Pillai’s Trace, Wilks’ Lambda, Hotelling Trace and Roy’s Largest Root statistical test demonstrated that there is a significant effect of the treatments composed of the mixture of organic and inorganic fertilizers on the average number of leaves and the average height of L. sativa L., since p < 0,05, at the α = 0,05 level. However, the results diverge from other studies that evaluated multiple response variables with one, two and three factors and did not apply multivariate analysis of variance, either in classical designs or in factorial experiments (Muscolo et al., 2022; Pizarro et al., 2019).
When performing the univariate analysis of variance in a complete randomized design, it was determined that the factor composed of organic and inorganic fertilizers significantly influenced both the average number of leaves and the average height of L. sativa L., since a p < 0,05 was obtained. In this regard, there is agreement with Giménez et al. (2019), regarding the univariate analysis of variance technique used for each of their response variables, which showed significant differences in lettuce yield, but divergence in terms of the design since it was a factorial experiment in a randomized complete block design.
Likewise, it coincided with Chinta et al. (2020), in reference to the application of univariate analysis of variance in its different response variables, however, they justified the significance of lettuce yield in a randomized complete block split-plot design. On the other hand, Majid et al. (2021), in their study evaluated multiple response variables and used the technique of univariate analysis of variance in a completely randomized design to measure the significance of lettuce plant growth parameters.
In the same way, experimental studies found significant differences between the average number of leaves, plant size and other characteristics in lettuce by treatment effect with the Tukey test (Abedin et al., 2021; Valderrama et al., 2020). In contrast, other experimental investigations of factorial type, determined with Fisher’s Least Significant Difference (LSD) in one of the treatments significant differences in their multiple response variables of lettuce growth and yield, although, the interactions between treatments or factors were not significant (Mpai et al., 2022; Nektarios et al., 2022).
The theory indicates that the proposed multivariate model must meet the assumptions of normality and multivariate homoscedasticity of the residuals (Cuadras, 2014). In this regard, the test for normality and multivariate homoscedasticity of the residuals determined p = 0,244 > 0,05 and p = 0,180 > 0,05, respectively. Consequently, it has been significantly demonstrated that there is multivariate normality as well as multivariate homoscedasticity of the residuals. Thus, it is concluded that there is sufficient evidence that the model is adequate. However, it is very frequently evidenced in experimental level research, where the effect of treatments on multiple response variables on yield, lettuce growth, and other plants is evaluated, and the non-specificity or non-compliance with the assumption of normality and homoscedasticity of the residuals in univariate form, even less in multivariate form (Bhunia et al., 2021; Gao et al., 2020; Liu et al., 2022). Nevertheless, (Garza-Alonso et al., 2023), mention in their research that they previously performed the Levene and Kolmogorov-Smirnov tests to verify the equality of variances and normal distribution of the data in the univariate form.
CONCLUSIONS
The highest average number of leaves was 21,2 ± 1,483, which was obtained with the treatment composed of the compost - diammonium phosphate mixture. Whereas the highest average height was 10,02 ± 0,666, which was achieved with the compost - diammonium phosphate fertilizer mixture. In addition, the organic and inorganic fertilizer mixtures showed multivariate effect on L. sativa L. growth, evaluated by Pillai’s Trace, Wilks’ Lambda, Hotelling Trace, and Roy’s Largest Root statistical tests (p < 0,05, in each case), showing vector differences of means of at least one treatment. Likewise, the experimental treatments showed a univariate effect on the L. sativa L. growth, both for the number of leaves (F=14,406; p < 0,000) and height (F=24,957; p < 0,000), generating mean differences of at least one treatment in each of the responses. In addition, Tukey’s univariate multiple comparisons test demonstrated the differences between treatments. Finally, the assumptions of the multivariate model were tested using the Doornik-Hansen test for multivariate normality (χ2 = 2,818; p = 0,244) and Box’s M test for homogeneity of covariance matrices (F = 1,406; p =0,180), which were satisfied in both cases. Therefore, the multivariate experimental model is suitable to evaluate the effect of organic and inorganic fertilizers on L. sativa L. growth.











 uBio
uBio