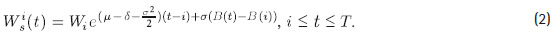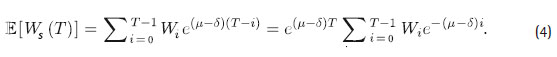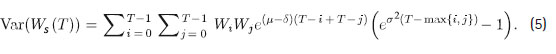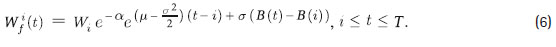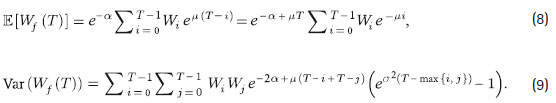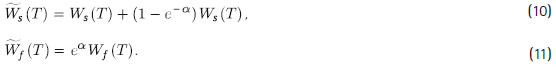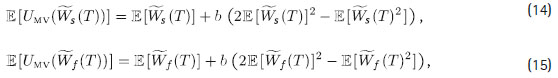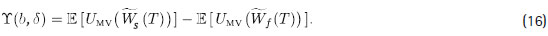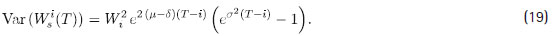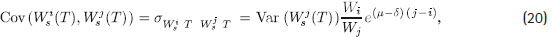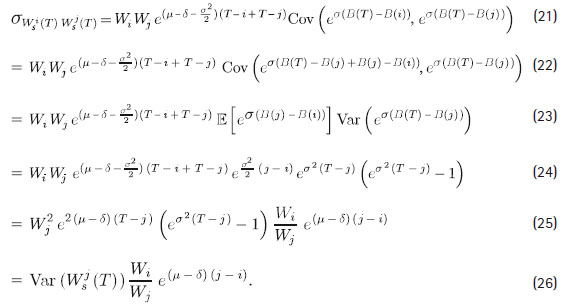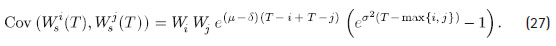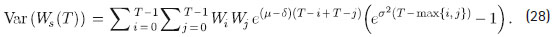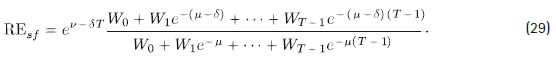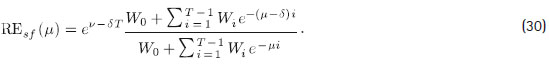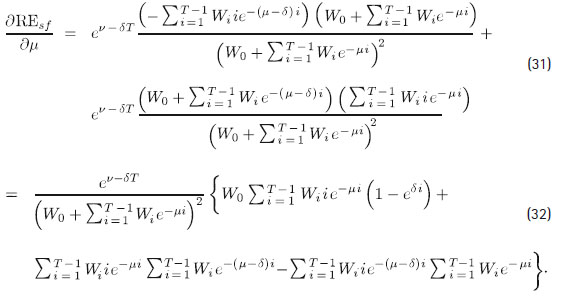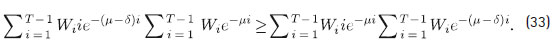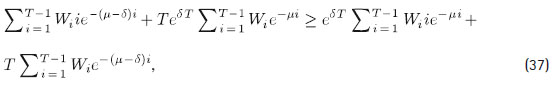Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Apuntes
versión impresa ISSN 0252-1865
Apuntes vol.43 no.78 Lima ene./jun. 2016
http://dx.doi.org/10.21678/0252-1865-00430078_3
ARTÍCULOS
Comparación de comisiones por flujo y por saldo en sistemas de pensiones con cuentas individuales de capitalización
Luis Chávez-Bedoya ESAN, Lima
Nelson Ramírez Rondán* Banco Central de Reserva del Perú, Lima
Resumen
En el presente artículo se desarrolla una metodología en tiempo discreto para comparar esquemas de cobro de comisiones por saldo y por flujo (sueldo) en la fase de acumulación de un fondo de pensiones bajo el sistema de cuentas individuales de capitalización. A partir de tal metodología, se estudia el efecto de la aversión al riesgo y otras variables relevantes en el desempeño e idoneidad de los tipos de comisión antes mencionados. Finalmente, se realiza una aplicación práctica y se muestran resultados en el marco del Sistema Privado de Pensiones del Perú, incluyendo comisiones de indiferencia y ratios de equivalentes de certeza.
Palabras clave: fondos de pensiones; comisión por flujo; comisión por saldo; cuentas individuales de capitalización.
1. INTRODUCCIÓN
Durante el último cuarto del siglo pasado, muchos países latinoamericanos reformaron sus sistemas pensionarios, migrando de sistemas públicos de reparto a sistemas privados con cuentas individuales de capitalización (CIC)1. Según Escrivá et al. (2010), a través de estos nuevos sistemas se buscaba adaptarse a los nuevos riesgos y retos que imponían a los países factores como: la vulnerabilidad de las finanzas públicas, los cambios en las tasas de natalidad, la mayor longevidad de la población, los problemas de eficiencia en la administración pública y el mayor desarrollo potencial de los mercados financieros. Sin embargo, actualmente se sugiere llevar a cabo una nueva serie de reformas, cuyos retos fundamentales, considerados en Kritzer et al. (2011), son aumentar la cobertura y competencia de los sistemas previsionales así como reducir sus costos de administración.
Dos características importantes de un sistema pensionario con CIC son, por un lado, el hecho de que el afiliado asume el riesgo derivado por la fluctuación del valor de los activos administrados y, por otro lado, el que los cargos administrativos (comisiones) cobrados por las administradoras de fondos de pensiones (AFP) tienen un impacto importante en el balance final de las CIC2. Más aún, como se menciona en James et al. (2001), Whitehouse (2001) y Mitchell (1998), una de las principales críticas a los sistemas con CIC es su elevado costo, pues este hecho no incentiva la participación, daña la imagen del sistema en su conjunto, reduce futuras pensiones e incrementa los costos futuros para el gobierno de existir una pensión mínima garantizada.
De acuerdo con Kritzer et al. (2011), los cargos administrativos más comunes en sistemas de pensiones con CIC son: proporcionales por flujo (expresados como un porcentaje del salario o contribución), fijos por flujo, proporcionales por saldo y proporcionales sobre rendimientos en exceso3. El presente artículo analiza únicamente las comisiones proporcionales por flujo y por saldo, las cuales son los tipos más comunes e importantes en Latinoamérica. Para Queisser (1998), la comisión por flujo es más ventajosa para las AFP en la fase inicial del sistema y, a pesar de que la comisión por saldo alinea los objetivos de las AFP en términos de incrementar la rentabilidad del fondo, ella tiende a ser más cara en el largo plazo debido a que las CIC se incrementan en valor. Además, Shah (1997) afirma que la comisión por flujo genera distorsiones y tendencias indeseables, como promover altos costos de instalación de las AFP, desalentar la competencia del sistema y generar pérdidas para los afiliados de mayor edad.
En el Perú, la reforma del Sistema Privado de Pensiones (SPP) de 1992 tuvo como objetivo proveer la sostenibilidad financiera que el sistema no tenía. Recientemente, y en el marco de la reforma del SPP, un punto importante del debate han sido las comisiones cobradas por las AFP. Entonces la regulación debería asegurar el tipo de comisión que genere mayor riqueza terminal del afiliado, siendo este un tema importante en el SPP.
La forma tradicional de comparar comisiones por saldo y por flujo es a través de una comisión por saldo equivalente neutral al riesgo, la cual iguala el valor esperado de los fondos (bajo ambos esquemas de cobro) al final del periodo de acumulación. Este enfoque se utiliza en Shah (1997), Diamond (2000), Blake y Board (2000), Whitehouse (2001), Devesa-Carpio et al. (2003) y Gómez-Hernández y Stewart (2008). Moloche (2012), a través de un modelo (o benchmark) que maximiza la utilidad terminal del afiliado en un contexto de optimización dinámica, compara algunos escenarios de las comisiones por flujo y por saldo, concluyendo empíricamente en el SPP que, bajo los niveles actuales de comisión por saldo, esta no sería conveniente para los afiliados menos aversos al riesgo.
Es en este contexto que la presente investigación considera dos métodos para comparar dichas comisiones y a su vez analiza su sensibilidad ante cambios de ciertos parámetros importantes, en especial la aversión al riesgo del afiliado. Los métodos de comparación se han considerado solo desde el punto de vista del afiliado4 y son la ratio de los valores esperados de riqueza terminal y la diferencia de utilidades esperadas de riqueza terminal. En la parte teórica, se han hecho una serie de supuestos que permiten derivar expresiones cerradas que explican el comportamiento de las comisiones bajo los métodos de comparación antes mencionados. Los supuestos más importantes son: el uso de un movimiento browniano geométrico (MBG) para el valor cuota del fondo y el hecho de que las preferencias del afiliado se puedan expresar en términos de la media y la varianza de la riqueza terminal. Posteriormente, en la aplicación práctica al SPP, se realiza un análisis de sensibilidad de las comisiones con respecto a ciertas variables fundamentales, pero relajando algunos supuestos, como el correspondiente a la función de utilidad del afiliado. En términos generales, se puede concluir que la comisión por saldo mejora su desempeño al incrementar la aversión al riesgo del afiliado, mientras que tasas de crecimiento más altas del valor cuota hacen preferible la comisión por flujo con respecto a la comisión por saldo en escenarios de neutralidad al riesgo.
La estructura del presente trabajo de investigación es la siguiente: en la sección 2 se propone una metodología de modelación y comparación de las comisiones por flujo y por saldo; luego la aplicación práctica de la metodología propuesta al SPP se realiza en la sección 3. Finalmente, en la sección 4 se concluye, se brindan ciertas recomendaciones y se proponen algunas extensiones para la metodología.
2. METODOLOGÍA
Considérese i e N y T e N +, tales que 0 ≤ i ≤ T - 1. El índice i representa un mes particular y T es el número de meses que faltan para la jubilación del afiliado. Se asume que el valor cuota, V, de un fondo de pensiones representativo de una AFP en el tiempo t ∈ R+ (meses) satisface la siguiente ecuación diferencial estocástica (EDE):
dV (t) = mv (t)dt + sv(t) dB(t),V(0) = V0, (1)
donde m es la tasa de crecimiento del valor cuota por unidad de tiempo (meses), s la volatilidad del retorno logarítmico mensual del mismo, V0 el valor cuota inicial y el proceso estocástico B es un movimiento browniano estándar unidimensional. La EDE en (1) es una especificación común para modelar el valor cuota, pues es muy utilizada en modelos de control estocástico para fondos de pensiones5.
A continuación se describe con detalle las comisiones por saldo y por flujo utilizando una estructura similar a la proporcionada en: Shah (1997), Diamond (2000), Blake y Board (2000), Whitehouse (2001), Devesa Carpio et al. (2003), y Gómez Hernández y Stewart (2008).
2.1. Comisión por saldo
Sea d > 0 la comisión por saldo mensual expresada en tiempo continuo6. Además, en el mes i el afiliado aporta una suma Wi > 0 a su fondo de capitalización individual. Si el valor cuota, V, se normaliza a la unidad en el periodo i, entonces el aporte Wi equivale al mismo número de cuotas. Es decir que para t ≥ i, y basándonos en la EDE (1), el aporte realizado en i seguiría el siguiente MBG:
Al afiliado le interesa determinar el valor final de su fondo, Ws (T ), el cual es la suma de los valores finales de todos los aportes realizados según la secuencia WT = {Wi | Wi > 0,0 ≤ i ≤ T - 1}. Entonces,
donde los procesos Wis en (2) están sujetos a la misma fuente de incertidumbre B dada por (1). Además, la esperanza, E [Ws (T ) ], del valor final del fondo es:
La varianza del fondo final del afiliado bajo comisión por saldo viene dada por:
Ver la demostración en el anexo A.
2.2. Comisión por flujo
Sea a > 0 la tasa de la comisión por flujo7. Si el afiliado realiza un aporte Wi en el mes i, la comisión que pagaría a la AFP (en el momento del aporte) sería igual a Ci = Wi (1 - e-a). Considerando que la comisión Ci pudo ser invertida en el fondo, el aporte del afiliado ajustado por el costo de oportunidad de Ci puede expresarse como e-a Wi . A partir de este supuesto, el aporte ajustado de la comisión por flujo en el mes i, Wif , evolucionaría según el siguiente MBG:
Para el afiliado es importante calcular el monto del fondo final ajustado por el costo de oportunidad de la comisión por flujo según la secuencia de aportes WT = {Wi | Wi > 0,0 ≤ i ≤ T - 1}. Si se denota dicho monto final como Wf (T ), entonces se tiene:
Utilizando (4) y la varianza del fondo final (5), se demuestra que la esperanza y la varianza de Wf (T ) se pueden calcular a través de las siguientes expresiones:
Es importante recalcar que Wf (T ) no representa el verdadero monto final del fondo del afiliado, sino uno ajustado por el costo de oportunidad de la comisión por flujo. Además, el fondo final del afiliado sería igual a eaWf (T ).
2.3. Factores de riesgo
Hasta este momento solo se ha considerado un factor de riesgo en el modelo: los rendimientos del valor cuota del fondo dado por (1). No se ha considerado aleatoriedad en la secuencia de aportes a pesar de que, generalmente, ella se expresa como un porcentaje de los salarios y estos, a su vez, se indexan a la inflación. Más aún, en un mercado con tasas de retorno estocásticas, es conocido que existe una correlación entre las tasas de inflación y el rendimiento de los activos8. Con esto, introducir aleatoriedad en los rendimientos pero no en las contribuciones podría llevar a falsas conclusiones, pues ambos procesos dependen de la inflación. Una alternativa es trabajar en términos de rendimientos nominales e imponer un proceso estocástico a las contribuciones, pero con cierta correlación con el valor cuota; sin embargo, hemos preferido hacerlo con una secuencia determinística de contribuciones y, para incluir la inflación, expresaremos y calibraremos el valor cuota y las contribuciones en términos reales.
2.4. Comparación de comisiones por saldo y por flujo
Considérese que un afiliado quiere estudiar la idoneidad de los esquemas de cobro de comisiones a partir de las riquezas terminales Ws (T ) y Wf (T ) dadas por (3) y (7), respectivamente. Es importante notar que al introducir el costo de oportunidad de la comisión por flujo en Wf (T ) las variables aleatorias antes mencionadas se vuelven comparables en cierto sentido; sin embargo, Wf (T ) no representa riqueza terminal sino riqueza terminal ajustada por un cierto costo de oportunidad. A partir de este hecho se consideran las siguientes variables aleatorias:
Notar que Ws (T ) en (10) es la suma del valor terminal del fondo bajo comisión por saldo, Ws (T ) y los valores terminales de las comisiones ahorradas con respecto a la comisión por flujo, (1 - e -a ) Ws (T ), las cuales se han reinvertido en la CIC del afiliado bajo el mecanismo de aportes voluntarios. Bajo este esquema, Ws (T ) representa la riqueza terminal del afiliado bajo comisión por saldo, asumiendo que el ahorro producido por las comisiones por flujo no desembolsadas se reinvierten en las mismas condiciones que los aportes regulares por saldo9. Por otro lado, Wf (T ) representa la verdadera riqueza terminal del afiliado bajo comisión por flujo. Entonces, a partir de las definiciones (10) y (11), se estarían comparando riquezas terminales bajo ambos tipos de comisión.
El resto de la sección profundizará la comparación de Ws (T ) y Wf (T ) a través de dos criterios: la ratio de valores esperados y la diferencia de utilidades esperadas.
2.4.1. Ratio de los valores esperados de riqueza terminal
Si la comparación se hace utilizando las esperanzas de las riquezas terminales Ws (T ) y Wf (T ), entonces se define:
Si REsf > 1, entonces la comisión por saldo sería preferible; si REsf < 1, entonces la comisión por flujo sería preferible. Asimismo, cuando REsf = 1, el afiliado sería indiferente frente a ambas alternativas. Notar que este criterio de comparación asume un afiliado con indiferencia al riesgo.
Se muestra que la ratio de valores esperados de la riqueza terminal, REsf , es decreciente a mayores tasas de crecimiento del valor cuota (ver el anexo B). Esto es, REsf es una función estrictamente decreciente en m y tal relación es independiente de la secuencia de aportes WT . Lo anterior implica que la comisión por flujo mejora con respecto a la comisión por saldo al incrementar la tasa de crecimiento del valor cuota. A continuación se define la comisión por saldo equivalente para un afiliado neutral al riesgo.
Para un conjunto de parámetros dados N = {T, a, m, s2, WT } y REsf , se define la comisión por saldo equivalente neutral al riesgo, dN (N), como el valor de la comisión por saldo, d, tal que REsf = 1. Además, si se quiere denotar dependencia explícita de dN (N) con respecto a T, a, o ambas, se puede utilizar dN (T ), dN (a) y dN (T, a), respectivamente. Asimismo, se utilizará dN cuando se refiera a la comisión equivalente en general10.
2.4.2. Utilidad esperada de riqueza terminal
Considérese un afiliado con aversión al riesgo y sea U (W ) su utilidad cuando una realización de riqueza terminal es igual a W > 0. Para determinar el tipo de comisión más apropiado, el afiliado necesita comparar las utilidades esperadas de riqueza terminal E U (Ws (T ) ) ] y E [U (Wf (T ) ) ]. Sin embargo, expresiones analíticas explícitas para dichas utilidades esperadas no se encuentran disponibles en general.
Debido a que se cuenta con fórmulas explícitas para el primer y segundo momento de las riquezas terminales Ws (T ) y Wf (T ) y que el objetivo es encontrar propiedades generalizables y/o fórmulas cerradas, entonces resulta apropiado considerar una función de utilidad cuadrática dada por:
UMV (W ) = aW - bW2, (13)
donde a > 0 y b > 0 es el coeficiente de aversión al riesgo. Notar que cuando b = 0 el afiliado sería neutral al riesgo. Además, se fija a = 1 + 2b E [W] de manera similar a Zhou y Li (2000). Si la utilidad de riqueza terminal, U, es como en (13), se tiene:
y las expresiones de E [Ws (T )2] y E Wf (T )2] se pueden derivar explícitamente.
Para un conjunto fijo de parámetros y la utilidad cuadrática en (13), se define Y como la diferencia entre E [UMV(Ws (T ) ) ] y E [UMV (Wf (T ) ) ] dados por (14) y (15), respectivamente.
Entonces, considerando Y como una función de la aversión al riesgo, b, y el nivel de la comisión por saldo, d, se tiene:
La función Y (b, d ) debe reducirse a medida que aumente la comisión por saldo, d, pues la comisión por flujo debe volverse preferible. Para ello se requieren supuestos que aseguren dicho resultado, estos son: T > 1, b > 0, y s 2 ≤ 1 ln(2) (ver la demostración formal en el anexo C). Luego, en forma similar a la definición de la comisión por saldo equivalente neutral al riesgo, se introduce la comisión por saldo equivalente aversa al riesgo como el valor de d que hace iguales a las utilidades esperadas de riqueza terminal bajo ambos esquemas. Tal medida ayudará a comprender el impacto que produce la aversión al riesgo al comparar ambos tipos de comisión.
Sea un conjunto de parámetros dados por A = N U {b}, en el cual se define la comisión por saldo equivalente aversa al riesgo, d * (A), como el valor de d que hace a E [UMV(Ws (T ) ) ] igual a E [UMV(Wf (T ) ) ]. Se demuestra que la comisión por saldo se vuelve más deseable con respecto a la comisión por flujo al aumentar la aversión al riesgo del afiliado (ver el anexo D). En otras palabras, lo anterior implica que si los valores esperados de riqueza terminal son idénticos, un afiliado que presenta aversión al riesgo preferiría la comisión por saldo y esta última se vuelve más atractiva con niveles más altos de aversión al riesgo. Además, la comisión por saldo que haría indiferente a los dos esquemas (en términos de utilidad esperada) bajo un cierto escenario es mayor que la comisión por saldo que iguala las riquezas terminales esperadas bajo el mismo escenario. Con lo cual, bajo los supuestos hechos, la comisión por saldo mejora su performance respecto a la comisión por flujo al aumentar la aversión al riesgo. Finalmente, es difícil generalizar los resultados teóricos de esta sección a otras funciones de utilidad distintas a UMV; sin embargo, en los experimentos numéricos se utiliza una función de utilidad CRRA (constant relative risk aversion) y se verifican empíricamente algunos de los resultados teóricos obtenidos en esta sección.
3. APLICACIÓN DE LA METODOLOGÍA AL SISTEMA PRIVADO DE PENSIONES DEL PERÚ
En esta sección se presenta la aplicación de la metodología propuesta al SPP. Esta aplicación es relevante debido a que el SPP está atravesando un proceso importante de reforma después de veinte años de ser creado11. Parte de la reforma consiste en el cambio de comisión por flujo a comisión por saldo, razón por la cual el presente trabajo de investigación analiza el efecto de ciertas variables en la comparación de dichas de comisiones.
3.1. Parámetros del modelo
Para las aplicaciones numéricas, se ha considerado una edad de jubilación de 65 años, la estructura actual de comisiones por flujo del SPP, la tasa de crecimiento real de los salarios y un escenario para el valor cuota, V, del fondo, el cual corresponde al fondo de riesgo medio (tipo 2) del SPP.
3.1.1. Calibración del MBG del valor cuota
Para implementar la metodología es necesario calcular los parámetros de crecimiento del valor cuota, m, y de la volatilidad de los retornos del valor cuota, s, del proceso estocástico del valor cuota del fondo descrito por la EDE (1). Es importante mencionar que un afiliado del SPP puede cambiar de fondo siempre y cuando después de los sesenta años de edad se mantenga en un fondo de bajo riesgo (tipo 1) del SPP. Asimismo, es posible incorporar en la metodología los cambios de fondo por parte del afiliado en un marco de optimización dinámica, pero en este documento se asume que el afiliado permanece en un mismo tipo de fondo durante toda la fase de acumulación.
Se emplean rendimientos logarítmicos históricos corregidos por inflación para estimar la volatilidad del respectivo MBG12. Para el escenario moderado de rentabilidad (fondo tipo 2), la volatilidad mensual de los rendimientos del valor cuota bajo un MBG es sM = 2,643%. Debido a la corta historia de los rendimientos de los fondos del SPP, es de esperar que la tasa de crecimiento (m) calibrada tenga un alto error de estimación. Por esta razón, y siguiendo las justificaciones del «Anexo técnico Nº 1» de la Superintendencia de Banca, Seguros y AFP (SBS 2013), se asume un rendimiento anual real para el escenario moderado igual a 5,0% anual (el rendimiento histórico real del fondo tipo 2 ha sido aproximadamente 6,0% anual).
Por teoría del MBG, se verifica que mM = rM + 0,5sM2 , donde rM es el rendimiento esperado mensual en tiempo continuo y el subíndice M hace referencia al fondo tipo 2. Después de las transformaciones adecuadas, se obtiene mM = 0,004415.
3.1.2. Comisión por flujo
Se han fijado tres niveles de comisión por flujo (expresados como porcentajes del salario del afiliado): fmin = 1,47%, fmax = 1,69% y fpro = 1,58%; los cuales corresponden al cargo mínimo, máximo y promedio por flujo del SPP al 16 de mayo de 2014. Como los trabajadores dependientes en el Perú están sujetos a una contribución obligatoria de 10% del salario y f i se aplica sobre este último, se tiene a = - ln (1 - 10f ), con lo cual amin = 0,1590, amax = 0,185 y apro = 0,172.
3.1.3. Crecimiento real de los salarios
La sucesión mensual de las contribuciones reales del afiliado (WT ) se asume tal que Wi +1 = (1 + ri )Wi para i ≥ 0 y W0 > 0 arbitrario. Los factores mensuales r se calculan a través de la suma del crecimiento correspondiente a lo largo de la curva de salario más un componente de ganancia por incremento de productividad. Asimismo, depende de diferentes clasificaciones de los afiliados según su género (M: mujer, H: hombre), nivel educativo (SU: sin estudios universitarios, U: con estudios universitarios) y edad. Los detalles de la calibración de los factores se muestran en SBS (2013), pero es importante mencionar que para afiliados jóvenes los factores promedio de crecimiento fluctúan entre 2,5% y 3,5% anual.
3.2. Resultados numéricos
A partir de los parámetros del modelo considerados en la sección 3.1., se determina primero la comisión por saldo equivalente neutral al riesgo, dN . Luego, se utiliza una función de utilidad de riqueza terminal del tipo CRRA para evaluar los equivalentes de certeza producidos por ambos tipos de comisión y el efecto que tiene en ellos la aversión al riesgo del afiliado.
3.2.1. Comisión por saldo equivalente neutral al riesgo (dN )
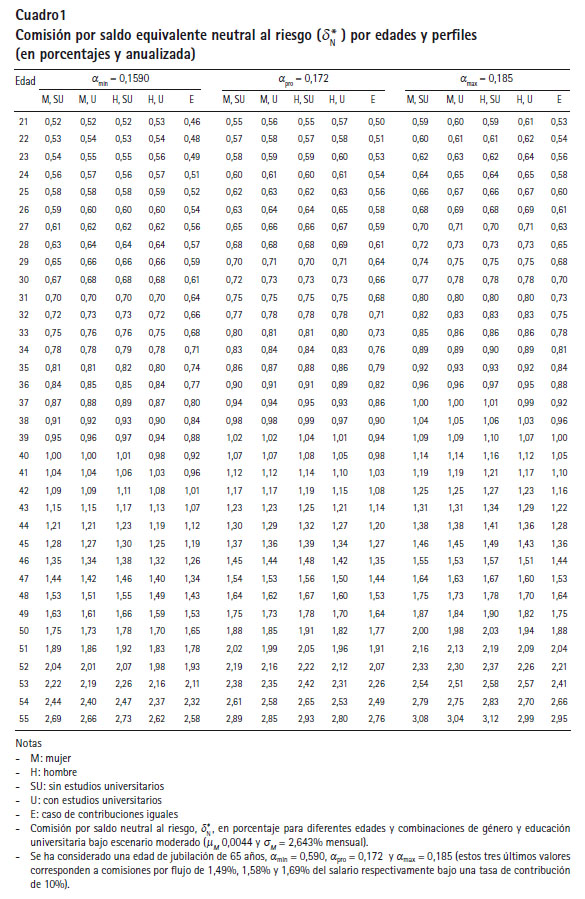
El Cuadro 1 muestra los valores de esta comisión, dN , anualizada y en porcentaje, para ciertas edades, cinco perfiles13, un escenario moderado (asume un rendimiento anual real del fondo igual a 5,0%) y tres valores distintos de comisión por flujo (amin = 0,1590, apro = 0,172 y amax = 0,185). Es importante notar que dN es independiente de la contribución inicial W0 > 0 . A partir del Cuadro 1 se observa que dN es estrictamente creciente con la edad (o estrictamente decreciente en T ) para un perfil de contribución y un nivel fijo de comisión por flujo, es decir que la comisión por saldo se vuelve más atractiva mientras mayor sea la edad de ingreso al sistema.
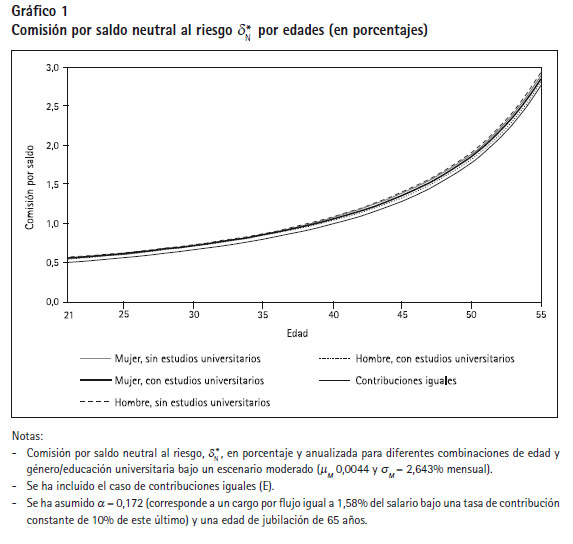
Considerando un afiliado de treinta años con perfil H, SU, se tiene dN = 0,68% anual para amin = 0,1590, dN = 0,73% para apro = 0,172 y dN = 0.78% para amax = 0,185. Por ejemplo, esto implica que, si se considera una comisión por flujo igual a amin, entonces un cargo por saldo menor a 0,68% haría preferible la comisión por saldo para todo afiliado que entra al sistema con una edad mayor a treinta años y perfil H, SU. Notar que dN > 0,52% para todos los escenarios del Cuadro 1 (sin considerar el perfil E). Tal valor corresponde a un afiliado de veintiún años con perfil M, SU y una comisión por flujo igual a amin. Es decir que un nivel de comisión por saldo menor o igual a 0,52% haría preferible tal comisión (para un afiliado neutral al riesgo) bajo todos los perfiles de contribución (sin E) y escenarios considerados en el estudio. El perfil de aportes iguales (E) beneficia a la comisión por flujo, pues los valores de dN generados son menores que los correspondientes a los otros perfiles. Este hecho se basa en que el crecimiento del salario puede considerarse como un incremento de la tasa de crecimiento m. Finalmente, y a manera de ejemplo, el gráfico 1 muestra la comisión por saldo equivalente neutral al riesgo, dN , como una función de la edad y del perfil de contribuciones, pero solo para la comisión por flujo promedio, aprom.
3.2.2. Comparación de equivalentes de certeza ( DCEsf )
En esta sección se va a estudiar de manera empírica la siguiente ratio:
donde CE [Ws(T ) ] y CE [Wf (T ) ] son los equivalentes de certeza de Ws (T ) y Wf (T ), asumiendo una función de utilidad de riqueza terminal arbitraria U, es decir que se satisface tanto E [U (Ws (T ) ) ] = U (CE[Ws (T ) ] ) como E [U (Wf (T ) ) ] = U (CE[Wf (T ) ] ). El valor de DCEsf bajo la función de utilidad cuadrática dada por (13) tiene expresión analítica explícita debido a que las expresiones para las medias y varianzas de Ws (T ) y Wf (T ) se encuentran disponibles y pueden utilizarse en (17). Pero, en este caso, DCEsf dependerá de W0 inclusive si se asume WT , como en la sección 3.1.3. En consecuencia, este hecho complica el estudio del comportamiento de DCEsf debido a cambios en el coeficiente de aversión al riesgo, b, de la función de utilidad cuadrática dada por (13).
Una alternativa para eliminar la dependencia de W0 es utilizar una función de utilidad tal que DCEsf sea independiente de W0 cuando WT se asume como en la sección 3.1.3. Si se considera una función de utilidad CRRA de la forma:
donde W > 0 es la riqueza terminal y Y > 0 es el coeficiente de aversión al riesgo, entonces DCEsf no dependerá de W0. Este hecho será importante para separar el efecto de la aversión al riesgo en DCEsf del causado por la contribución inicial W0. Es importante mencionar que expresiones cerradas para CE [Ws (T ) ] y CE [Wf (T ) ] no están disponibles para la utilidad (18), con lo cual se tendrá que utilizar simulación para obtener un estimador de DCEsf en (17). Además, en la literatura de administración de fondos de pensiones es más común y apropiado el uso de una utilidad CRRA, como en (18), que la cuadrática dada por (13).
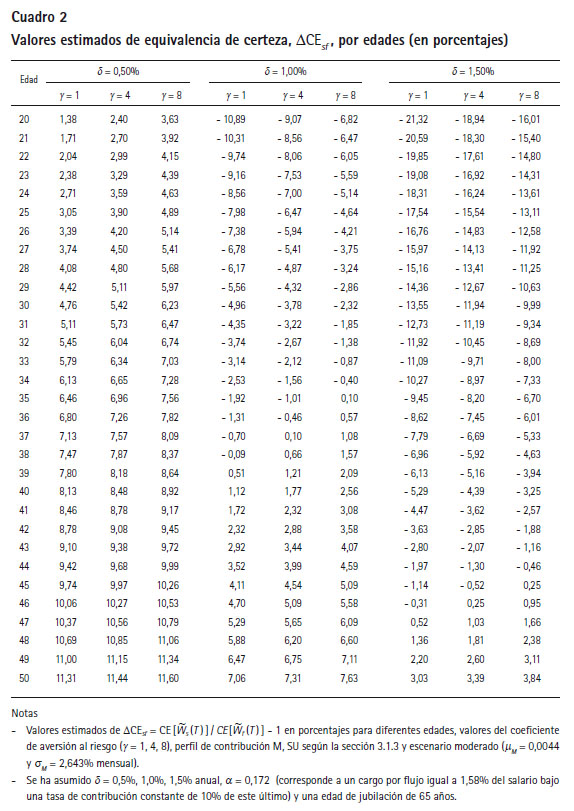
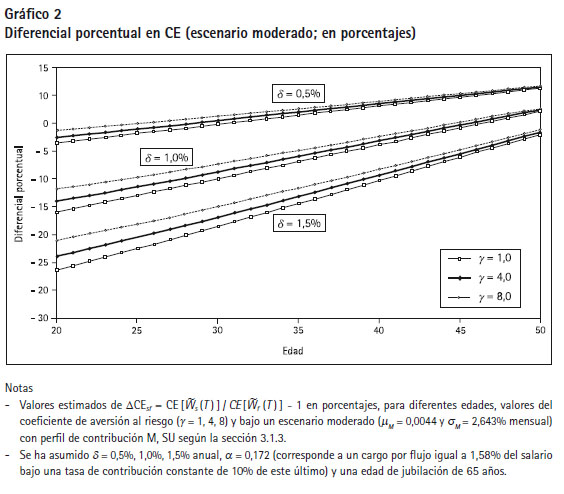
El Cuadro 2 presenta los valores estimados de DCEsf para diferentes edades, el perfil de contribuciones M, SU (como los resultados para los otros perfiles de la sección 3.1.3. son muy similares, estos no se han reportado) y bajo el escenario moderado de rentabilidad descrito en la sección 3.1.1. Siguiendo a Poterba et al. (2005), se consideran tres valores distintos de aversión al riesgo del afiliado: Y = 1 para un grado bajo; y en este caso U (W ) = ln (W ), Y = 4 para un grado moderado; y Y = 8 para un grado alto. El nivel de la comisión por saldo, d, se fija en tres valores: 0,5%, 1,0% y 1,5% anual, mientras que el nivel de la comisión por flujo se fija en apro = 0,172 (valor promedio actual del SPP). El número de caminos muestrales de la riqueza utilizado para estimar DCEsf se determinó utilizando el procedimiento secuencial de Kelton y Law (2000) con un error relativo de 0,0001 y un nivel de confianza de 99%. Asimismo, el gráfico 2 resume toda la información contenida en el Cuadro 2.
A partir de la información brindada, se puede observar que DCEsf es una función creciente en el grado de aversión al riesgo, Y, para una edad y un nivel de comisión por saldo fijos, lo cual corrobora empíricamente el hecho de que a mayor aversión al riesgo la comisión por saldo mejora con respecto a su par por flujo. Sin embargo, no se obtiene DCEsf > 0 para toda edad, pues se está fijando d en ciertos valores fijos en vez de trabajar con la comisión por saldo neutral al riesgo, d*N , correspondiente a cada edad. Asimismo, al disminuir d, la comisión por saldo se vuelve más atractiva, pues las curvas de DCEsf para un Y fijo suben. También se observa que la pendiente de DCEsf tiende a ser positiva, mantenerse constante con la edad y disminuir ligeramente al incrementar el grado de aversión al riesgo del afiliado. Es importante notar que d = 0,5% garantiza que DCEsf > 0 para toda edad y nivel de aversión al riesgo considerado. Además, cuando d = 1%, la edad para la indiferencia entre comisiones fluctúa entre 35 años (Y = 8 ) y 38 años (Y = 1). Cuando d = 0,5%, la edad de indiferencia se encuentra alrededor de 45 años (Y = 8) y 47 años (Y = 1). Se debe recordar que los afiliados con edad menor a la de indiferencia preferirán la comisión por flujo. Si d = 1% y la comisión por flujo es 1,58% del salario (promedio del SPP a mayo de 2014), un afiliado con veinte años de edad experimentaría una pérdida porcentual en equivalente de certeza en el rango de 7% (Y = 8) a 11% (Y = 1); mientras que si la comisión es d = 1,5%, la pérdida estaría en el rango de 16% (Y = 8) a 21% (Y = 1).
4. CONCLUSIONES
En el presente artículo se ha desarrollado una metodología en tiempo discreto que permite comparar comisiones por flujo y por saldo en sistemas de pensiones con CIC. Los métodos de comparación considerados fueron la ratio de valores esperados de riqueza terminal y la diferencia de utilidades esperadas de riqueza terminal. En muchos casos se obtienen resultados muy generales en cuanto al desempeño relativo de los esquemas de comisión y estos se logran sin necesidad de asumir un patrón particular en la secuencia de aportes. Además, se brindan fórmulas y/o expresiones que permiten determinar el tipo de comisión que sería conveniente para cada afiliado. A partir del uso de una función de utilidad cuadrática, se demuestra teóricamente que, por lo general, los incrementos de aversión al riesgo mejoran el desempeño de la comisión por saldo con respecto a su par por flujo, resultado acorde con la conclusión empírica de Moloche (2012).
A partir del desarrollo teórico realizado y de su aplicación práctica al SPP, se puede afirmar que una comisión por saldo igual a 0,5% anual haría conveniente al esquema por saldo sobre su par por flujo en casi todo escenario del estudio; esto considerando un cobro por flujo igual a 15,80% de los aportes (promedio del SPP a mayo de 2014). A tal nivel de comisión por flujo y cuando la comisión por saldo es igual a 1% anual, los afiliados menores de 37 años (aproximadamente) preferirán el cobro por flujo; pero cuando la comisión es 1,5% anual, la edad de indiferencia pasa a ser 45 años (aproximadamente). Más aún, un afiliado que ingresa al sistema a los 20 años bajo una comisión por saldo igual a 1% anual podría perder entre 7% y 11% en equivalente de certeza de riqueza terminal respecto a la comisión por flujo. Si dicha comisión es 1,5% anual, la pérdida porcentual estaría entre 16% y 21%. Es importante mencionar que los valores inferiores y superiores de los rangos corresponden a un nivel alto y bajo de aversión al riesgo, respectivamente.
Es posible hacer muchos refinamientos a la metodología y a los métodos de comparación. Por ejemplo, se podría considerar comisiones variables por saldo según la evolución de las comisiones equivalentes desde la perspectiva de la AFP, comisión por resultados que depende estrictamente de la bolsa, procesos estocásticos más sofisticados para el valor cuota y las variables económicas relevantes. Asimismo, sería interesante contrastar los esquemas utilizando políticas óptimas que permitan cambiar el nivel de riesgo y rendimiento del fondo de acuerdo a la edad del afiliado y al tamaño del fondo, en un contexto de optimización estocástica en tiempo discreto. En esta línea también se podría profundizar el estudio de Moloche (2012) para diferentes edades y tasas de reinversión de las comisiones ahorradas por flujo. Más aún, es posible trabajar bajo el supuesto de compleción del mercado y brindar expresiones para determinar comisiones de indiferencia utilizando valuación en ausencia de oportunidades de arbitraje. Pero dichas extensiones escapan de los alcances del presente trabajo de investigación.
ANEXOS
Anexo A
Demostración de la varianza de la riqueza terminal
Para el cálculo de Var (Ws (T ) ), es necesario calcular la varianza de Wis (T ) y la covarianza entre Wis (T ) y Wis (T ) . Como Wis (T ) tiene una distribución log-normal, entonces:
Asimismo, se quiere verificar que para j > i y Wj > 0:
donde el GBM Wis se define en (2).
A partir de las propiedades de Wis , se tiene:
Para obtener (23) se utiliza el hecho de que B (T ) - B ( j ) es independiente de B ( j ) - B (i ).
Las fórmulas (19) y (20) generan la siguiente expresión para la covarianza de los valores finales de los aportes i y j para todo 0 ≤ i ≤ T - 1 y 0 ≤ j ≤ T - 1:
Utilizando (27), se puede calcular la varianza de Ws (T ) a través de:
Anexo B
Demostración de la derivada de REsf (m) con respecto a m es negativa
Sea v = ln(2 - e -a). Para el caso de aportes según la secuencia WT y cuando T > 1, se puede expresar REsf en (12) de la siguiente forma:
Se tiene que, a partir de la expresión dada en (29):
La derivada parcial de REsf (m) con respecto a m es:
Como d > 0 y Wi > 0 para todo i, es claro que W0 Procediendo por inducción, para T = 2 en (33) se tiene: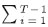 Wiie -mi (1-edi) < 0 para T > 1. Con lo cual, para demostrar que
Wiie -mi (1-edi) < 0 para T > 1. Con lo cual, para demostrar que 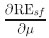 < 0, solo faltaría verificar que:
< 0, solo faltaría verificar que:
W1e-(m-d)W1e -m ³ W1e-mW1e-(m-d) (34)
Asumiendo que se cumple (33), se debe demostrar que:
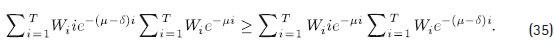
La desigualdad (35) es equivalente a:
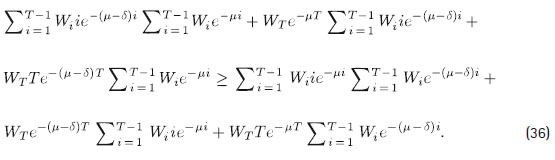
Como se asume (33) y WT > 0, la desigualdad (36) implica:
la cual a su vez es equivalente a:
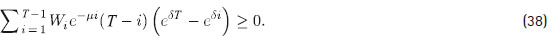
Para finalizar, se observa que la desigualdad (38) se cumple, pues T - i ≥ 1, Wi > 0 y d > 0.
Anexo C
Monotonicidad de Y (b, d ) con respecto a d
A partir de la definición de Y dada por (16), se tiene:
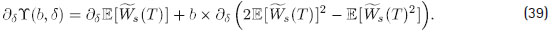
Como ∂d E [Ws (T ) ] < 0 para el escenario A y se asume b > 0 , solo se debe establecer las condiciones para que ∂d(2 E [Ws (T ) ]2 - E [Ws (T )2 ] ) ≤ 0. Utilizando las expresiones para E [Ws (T ) ]2 y E [Ws (T )2 ], se verifica que:
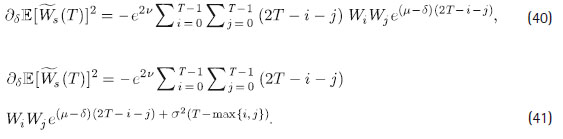
A partir de los resultados previos y después de algunas simplificaciones, se obtiene:
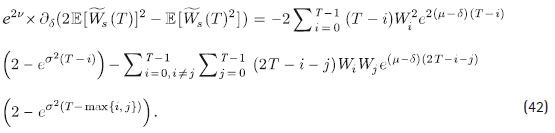
Finalmente, (42) será menor o igual a cero si 2 - e s2 (T - i ) ≥ 0 para todo i, lo cual se cumple cuando 2 - e s2T ≥ 0 .
Anexo D
A mayor aversión al riesgo, la comisión por saldo es preferible a la comisión por flujo
Primero se define las siguientes ratios:
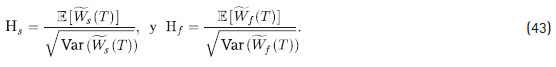
Si d se fija en el nivel dado por dN* y se utiliza el hecho de que Hs > Hf (la demostración se puede solicitar a los autores), entonces se tiene E [Wf (T ) ] = E [Ws (T ) ], E [Wf (T )2] > E [Ws(T)2] y:
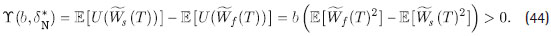
Como el lado derecho de (44) es positivo y creciente en b, se tiene Y (b, d * ) > 0 y además ∂b Y (b, dN*> 0. Luego, para d > 0, se define la función L (d) como:
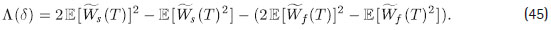
A partir de las demostraciones previas, se sabe que si s2 ≤ 1/T ln(2), entonces ∂d L (d ) < 0. Más aún, va a existir d * > d N , tal que L(d * ) = 0. Para cualquier b > 0 , se tiene:
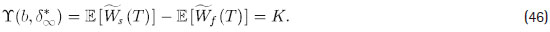
Notar que K < 0 y es independiente de b . Si se toma dos valores arbitrarios del coeficiente de aversión al riesgo b1 > 0 y b2 > 0 , tales que b1 > b2 y d ∈ (dN* , d¥* ), entonces se puede afirmar que Y (b1, d ) > Y (b2 , d ) con d dentro del intervalo previamente establecido y, además, que d * (b1) > dA* (b2). Notar que ambos, dA * (b1) y dA * (b2) existen porque Y (b, dN * ) > 0, Y (b, d¥* ) < 0 y ∂d Y (b, d ) < 0 para cualquier b > 0.
Siglas usadas
AFP Administradora de fondos de pensiones
APE Asociación Peruana de Economía
BCRP Banco Central de Reserva del Perú
CIC Cuenta individual de capitalización
CRRA Constant relative risk aversion (por sus siglas en inglés; aversión al riesgo constante y relativa)
EDE Ecuación diferencial estocástica
MBG Movimiento browniano geométrico
SBS Superintendencia de Banca, Seguros y AFP
SPP Sistema Privado de Pensiones
REFERENCIAS
ARENAS DE MESA, Alberto y Carmelo MESA-LAGO
2006 «The Structural Pension Reform in Chile: Effects, Comparisons with other Latin American Reforms, and Lessons». En: Oxford Review of Economic Policy, vol. 22 Nº 1, pp. 149-167. [ Links ]
ARRAU, Patricio; Salvador VALDÉS-PRIETO y Klaus SCHMIDT-HEBBEL
1993 «Privately Managed Pension Systems: Design Issues and the Chilean Experience» [mimeo.]. Reporte técnico. Washington D. C.: World Bank. [ Links ]
BATTOCCHIO, Paolo y Francesco MENONCIN
2004 «Optimal Pension Management in a Stochastic Framework». En. Insurance: Mathematics and Economics, vol. 34, Nº 1, pp. 79-95. [ Links ]
BLAKE, David y John BOARD
2000 «Measuring Value Added in the Pensions Industry». En: Geneva Papers on Risk and Insurance- Issues and Practice, vol. 25, Nº 4, pp. 539-567. [ Links ]
BLAKE, David; Andrew J. G. CAIRNS y Kevin DOWD
2001 «Pensionmetrics: Stochastic Pension Plan Design and Value-at-risk During the Accumulation Phase». En: Insurance: Mathematics and Economics, vol. 29, Nº 2, pp. 187-215. [ Links ]
BOUDOUKH, Jacob y Matthew RICHARDSON
1993 «Stock Returns and Inflation: A Long-horizon Perspective». En: The American Economic Review, vol. 83, Nº 5, pp. 1346-1355. [ Links ]
CAIRNS, Andrew J. G.; David BLAKE y Kevin DOWD
2006 «Stochastic Lifestyling: Optimal Dynamic Asset Allocation for Defined Contribution Pension Plans». En: Journal of Economic Dynamics and Control, vol. 30, Nº 5, pp. 843-877. [ Links ]
CORVERA, F.; J. LARTIGUE y D. MADERO
2006 «Análisis comparativo de las comisiones por administración de los fondos de pensiones en los países de América Latina» [mimeo.] México. [ Links ]
DEVESA-CARPIO, José Enrique; R. RODRÍGUEZ-BARRERA y Carlos VIDAL-MELIÁ
2003 «Medición y comparación internacional de los costes de administración para el afiliado en las cuentas individuales de capitalización». En: Revista Española de Financiación y Contabilidad, vol. XXXII, Nº 116, pp. 95-144. [ Links ]
DEVOLDER, Pierre; Manuela BOSCH PRINCEP e Inmaculada DOMÍNGUEZ FABIÁN
2003 «Stochastic Optimal Control of Annuity Contracts». En: Insurance: Mathematics and Economics, vol. 33, Nº 2, pp. 227-238. [ Links ]
DIAMOND, Peter
2000 «Administrative Costs and Equilibrium Charges with Individual Accounts». En: SHOVEN, J. (ed.). Administrative Aspects of Investment-based Social Security Reform. Chicago: University of Chicago Press, pp. 137-172. [ Links ]
DIAMOND, Peter y Salvador VALDÉS-PRIETO
1994 «Social Security Reforms». En: BOSWORTH, B. P.; R. DORNBUSCH y R. LABÁN (eds.). The Chilean Economy: Policy Lessons and Challenges. Washington D. C.: The Brookings Institution, pp. 257-328. [ Links ]
EDWARDS, Sebastian
1998 «The Chilean Pension Reform: A Pioneering Program. En: FELDSTEIN, M. (ed.). Privatizing Social Security. Chicago: University of Chicago Press, pp. 33-62. [ Links ]
ESCRIVÁ, José Luis; Eduardo FUENTES y Alicia GARCÍA-HERRERO
2010 «A. Balance de las reformas de pensiones en Latinoamérica». En: BBVA (ed.). Las reformas de los sistemas de pensiones en Latinoamérica: avances y temas pendientes. Madrid: BBVA, pp. 11-39. [ Links ]
FAMA, Eugene y G. William SCHWERT
1977 «Asset Returns and Inflation». En: Journal of Financial Economics, vol. 5, Nº 2, pp. 115-146. [ Links ]
GESKE, Robert y Richard ROLL
1983 «The Fiscal and Monetary Linkage Between Stock Returns and Inflation». En: The Journal of Finance, vol. 38, Nº 1, pp. 1-33. [ Links ]
GÓMEZ-HERNÁNDEZ, Denise y Fiona STEWART
2008 «Comparison of Costs and Fees in Countries with Private Defined Contribution Pension Systems». Documento de trabajo. París: International Organisation of Pension Supervisors. [ Links ]
HABERMAN, Steven y Elena VIGNA
2002 «Optimal Investment Strategies and Risk Measures in Defined Contribution Pension Schemes». En: Insurance: Mathematics and Economics, vol. 31, Nº 1, pp. 35-69. [ Links ]
HAN, Nan-wei y Mao-wei HUNG
2012 «Optimal Asset Allocation for DC Pension Plans Under Inflation. En: Insurance: Mathematics and Economics, vol. 51, Nº 1, pp. 172-181. [ Links ]
JAMES, Etelle; James SMALHOUT y Dimitri VITTAS
2001 «Administrative Costs and the Organization of Individual Retirement Account Systems: A Comparative Perspective». Documento de trabajo sobre investigación de políticas Nº 2554. Nueva York: World Bank. [ Links ]
KAY, Stephen y Barbara KRITZER
2001 «Social Security in Latin America: Recent Reforms and Challenges. En: Federal Reserve Bank of Atlanta Economic Review, vol. 86, Nº 1, pp. 41-52. [ Links ]
KELTON, W. David y Averill M. LAW
2000 Simulation Modeling and Analysis. Boston: McGraw Hill. [ Links ]
KRITZER, Barbara; Stephen KAY y Tapen SINHA
2011 «Next Generation of Individual Account Pension Reforms in Latin America». En: Social Security Bulletin, vol. 71, Nº 1, pp. 35-76. [ Links ]
MARTHANS, Juan y José STOK
2013 «Una propuesta para reformar los sistemas privados de pensiones: el caso peruano». Documento de trabajo. Piura: Universidad de Piura. [ Links ]
MARTÍNEZ, Óscar y Andrés MURCIA
2008 «Sistema de comisiones de las administradoras de fondos de pensiones en Colombia». Reporte de estabilidad financiera. Bogotá: Banco de la República de Colombia. [ Links ]
MASÍAS, Lorena y Elio SÁNCHEZ
2007 «Competencia y reducción de comisiones en el sistema privado de pensiones: el caso peruano». Documento de trabajo Nº DT/02/2006. Lima: SBS. [ Links ]
MESA-LAGO, Carmelo
2006 «Private and Public Pension Systems Compared: An Evaluation of the Latin American Experience ». En. Review of Political Economy, vol. 18, Nº 3, pp. 317-334. [ Links ]
MITCHELL, Olivia
1998 «Administrative Costs in Public and Private Retirement Systems». En: FELDSTEIN, M. (ed.). Privatizing Social Security. Chicago: University of Chicago Press, pp. 403-456. [ Links ]
MOLOCHE, Guillermo
2012 Política óptima de inversiones de las AFPs: implicancias del marco regulatorio y los esquemas de comisiones. Lima: CIES. [ Links ]
MURTHI, Mamta; J. Michael ORSZAG y Peter R. ORSZAG
2001 «Administrative Costs Under a Decentralized Approach to Individual Accounts: Lessons from the United Kingdom». En: HOLZMANN, R. y J. STIGLITZ (eds.). New Ideas about Old Age Security. Nueva York: The World Bank, pp. 308-335. [ Links ]
POTERBA, James; Joshua RAUH; Steven VENTI y David WISE
2005 «Utility Evaluation of Risk in Retirement Saving Accounts». En: WISE, D. (ed.). Analyses in the Economics of Aging. Chicago: University of Chicago Press, pp. 13-58. [ Links ]
QUEISSER, Monika
1998 «Regulation and Supervision of Pension Funds: Principles and Practices. En: International Social Security Review, vol. 51, Nº 2, pp. 39-55. [ Links ]
SBS
2013 «Anexo técnico 1. Metodología aplicable a los cálculos del aplicativo de comparación de comisiones». Lima: SBS. [ Links ]
SHAH, Hemant
1997 «Towards Better Regulation of Private Pension Funds». Documento de trabajo sobre investigación de políticas Nº 1791. Nueva York: World Bank. [ Links ]
SINHA, Tapen
2001 «Analyzing Management Fees of Pension Funds: A Case Study of Mexico». En: Journal of Actuarial Practice, Nº 9, pp. 5-43. [ Links ] 2000 Pension Reform in Latin America and its Lessons for International Policymakers, vol. 23. Dordrecht: Kluwer Academic Publishers.
TAPIA, Waldo y Juan YERMO
2008 «Fees in Individual Account Pension Systems: A Cross-country Comparison». Documento de trabajo sobre aseguramiento y pensiones privadas Nº 27. París: OECD Publishing. [ Links ]
VIGNA, Elena
2014 «On Efficiency of Mean-variance Based Portfolio Selection in Defined Contribution Pension Schemes. En: Quantitative Finance, vol. 14, Nº 2, pp. 237-258. [ Links ]
WHITEHOUSE, Edward
2001 «Administrative Charges for Funded Pensions: Comparison and Assessment of 13 Countries. En: Private Pension Systems: Administrative Costs and Reforms, Private Pensions Series. OECD, Nº 2, pp. 85-154. [ Links ]
ZHOU, X. Y. y D. LI
2000 «Continuous-time Mean-variance Portfolio Selection: A Stochastic LQ Framework». En: Applied Mathematics and Optimization, vol. 42, Nº 1, pp. 19-33. [ Links ]
* Artículo remitido el 17 de abril de 2015 y aprobado para su publicación el 11 de marzo de 2016. Los autores agradecen a Guillermo Moloche y al evaluador de la revista Apuntes por sus valiosos comentarios, así como a los participantes del seminario de investigación del Banco Central de Reserva del Perú (BCRP), del XXXI Encuentro de Economistas del BCRP y del congreso anual 2014 de la Asociación Peruana de Economía (APE) por los comentarios y discusiones que enriquecieron este trabajo. Los posibles errores son responsabilidad de los autores.
Luis Chávez-Bedoya es PhD en Management Sciences por la Northwestern University. Actualmente es profesor de finanzas en ESAN Graduate School of Business. Sus investigaciones han sido publicadas en Quantitative Finance, Journal of Pension Economics and Finance, Cepal Review, Estudios de Economía de la Universidad de Chile y Journal of Asset Management, entre otras revistas especializadas. Correo electrónico: lchavezbedoya@esan.edu.pe
Nelson Ramírez Rondán es doctor en Economía por la University of Wisconsin-Madison. Se desempeña como investigador de la Subgerencia de Investigación Económica del BCRP. Sus áreas de interés son la econometría teórica y la macroeconomía empírica. Correo electrónico: nramron@gmail.com
1. El caso más documentado es Chile. El lector puede encontrar los aspectos principales de tal reforma en: Arrau et al. (1993); Diamond y Valdés-Prieto (1994); Edwards (1998); Arenas de Mesa y Mesa-Lago (2006). En el caso del Perú, un análisis completo de la reforma del sistema de pensiones y su estado actual se expone en Marthans y Stok (2013). Queisser (1998), Sinha (2000), Kay y Kritzer (2001), Mesa- Lago (2006) y Kritzer et al. (2011) son buenas referencias para el estudio de la reforma, situación y perspectiva de los sistemas pensionarios de América Latina.
2. Devesa-Carpio et al. (2003) consideran que el sistema de cobro adoptado en el sistema con CIC es muy importante debido a que el proceso de acumulación es exponencial y dirigido hacia horizontes largos de tiempo. Por ejemplo, Murthi et al. (2001) estiman que en el Reino Unido más del 40% del valor de la CIC se disipa a través de cobros de administración, mientras que Whitehouse (2001) determina que un cobro de 1% anual de los activos representa cerca del 20% del valor final de la pensión.
3. Análisis y comparaciones de cargos administrativos en diferentes países se pueden encontrar en: James et al. (2001); Whitehouse (2001); Gómez-Hernández y Stewart (2008); Corvera et al. (2006); Tapia y Yermo (2008); Devesa-Carpio et al. (2003). Además, Sinha (2001), Masías y Sánchez (2007) y Martínez y Murcia (2008) evalúan en detalle (a pesar de que se han realizado modificaciones) los cargos administrativos en México, Perú y Colombia, respectivamente.
4. Un análisis completo acerca de la conveniencia de alguna de las comisiones sobre la economía se haría dentro de un modelo de equilibrio general.
5. Es un supuesto común en la literatura el asumir el MBG como proceso para el valor cuota del fondo o para los precios de los activos que conforman el fondo. Algunos ejemplos del uso del MBG son: Blake et al. (2001), Devolder et al. (2003), Vigna (2014), Haberman y Vigna (2002), Battocchio y Menoncin (2004), Han y Hung (2012) y Cairns et al. (2006), entre otros. En el caso del estudio del SPP, Moloche (2012) utiliza en su metodología diferentes MBG para modelar los activos de renta variable nacional e internacional.
6. Un valor constante de d podría implicar que el sistema ha alcanzado madurez con respecto a esta forma de cobro.
7. También se le conoce como comisión por sueldo y puede ser cobrada como un porcentaje del salario o de la contribución del afiliado.
8. Está bien documentado que la inflación esperada, los shocks no esperados en ella y los cambios en la inflación esperada se correlacionan negativamente con el retorno de las acciones. Ver: Fama y Schwert (1977) y Geske y Roll (1983). Sin embargo, Boudoukh y Richardson (1993) encontraron evidencia que sugiere que los retornos nominales de largo plazo de las acciones están positivamente correlacionados con la inflación de largo plazo ex ante y ex post.
9. Por ejemplo, Moloche (2012) asume que el ahorro de las comisiones por flujo con respecto al de las comisiones por saldo se deposita en una cuenta de ahorros con características distintas e independientes al fondo de pensiones.
10. Notar que
d * (T = 1, a) = v y ∂adN * (T, a) > 0) para cualquier escenario N; y desde que la ratio de valores esperados de la riqueza terminal, REsf , es decreciente a mayores tasas de crecimiento del valor cuota, m, entonces se tiene que ∂m dN* (T, m) < 0 para T > 1.11. La Ley Nº 29903 contiene los principales aspectos de la reforma, uno de los cuales es que los afiliados migrarán a una comisión mixta, la cual tiene un componente por flujo transitorio decreciente de diez años y a partir del décimo año el cargo será únicamente por saldo. La reforma también incluye el mecanismo de subasta de las nuevas CIC y normas para incorporar a trabajadores independientes.
12. Las series de rendimientos históricos del valor cuota utilizadas corresponden a AFP Integra debido a que constituye un benchmark adecuado para el SPP y además fue la única AFP que se mantuvo (o no se fusionó) desde el inicio de las observaciones históricas disponibles. En el caso del fondo tipo 2, se consideran observaciones del valor cuota del 2 de febrero de 2001 al 30 de abril de 2014.
13. Los perfiles de contribución considerados son: M, SU; M, U; H, SU; H, U; y E. Los cuatro primeros se describen en la sección 3.1.3 y E corresponde a una secuencia de contribuciones reales iguales a W0 > 0.