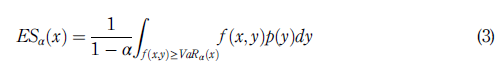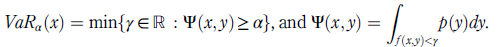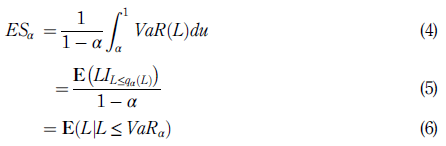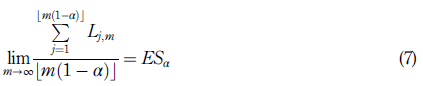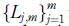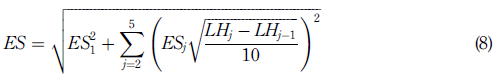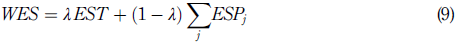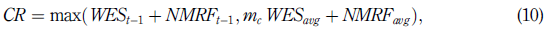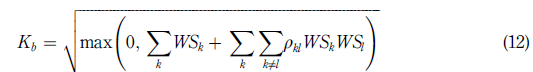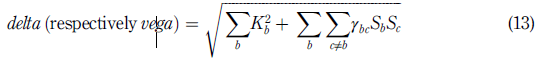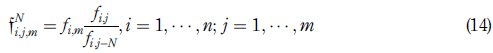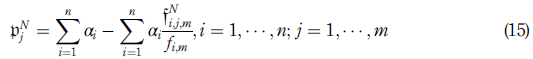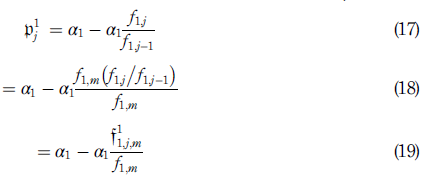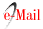Introduction
Basel Committee on Banking Supervision (BCBS) consolidated in 2019 the Fundamental Review of the Trading Book in BIS (2019) (FRTB) to improve the design and consistency of capital standards for market risk. FRTB regulation introduces a new approach to the current market risk management models, whose implementation is planned as of 1 January 2023. The regulation incorporates three fundamental aspects.
The first aspect differentiates between the trading book and the banking book. It accurately identifies which instruments are assigned to each and avoids arbitrage opportunities among the estimated capital requirements.
The second change considers the internal models approach (IMA) to measure market risk, a scheme that the regulator must previously approve. At this point, the regulation replaces the value at risk (VaR) and stressed value at risk (sVaR) measures established by Basel 2.5. Instead, it estimates the total capital requirement based on the aggregation of the following three requirements: expected shortfall (ES), non-modellable risk factors (NMRF) and default risk capital (DRC).
The third aspect is the mandatory adoption of the standardised approach (SA) to determine capital for market risk. The total capital requirement is, in turn, defined in terms of the aggregation of the following three expositions: sensitivities-based method (SbM) through the measure of delta, vega and curvature risks; default risk capital (DRC); and residual risk add-on (RRAO).
In BCBS (2019), based on a sample of banks, the future impact of FRTB implementation was estimated in January 2019. From there, risk-weighted assets increased from 4.4% in Basel 2.5 to 5.3% in FRTB, concerning total risk-weighted assets in Basel III. In addition, the average increase in risk capital is 22% compared to Basel 2.5. In FRTB, the risk capital under SA is considerably higher (over 60% on average) than the respective capital under IMA. Moreover, further increases in risk capital are estimated for small banks using a simplified version of the standardised approach.
Some progress has been made regarding the study of market risk. For example, concerning the FRTB internal models approach, ES metric is a consistent risk measure based on Artzner et al.’s (1999) and Rockafellar and Uryasev's (2000, 2002, 2013) works. Furthermore, a comparative analysis between the best known VaR metric and ES can be seen in Embrechts et al. (2018, 2020), and different estimation methods and ES models are documented, for example, in Patton et al. (2019), Nadarajah et al. (2014), Chen (2008) and Scaillet (2004). Further, FRTB requires the implementation of back-testing procedures to test the reliability of VaR measures. In this direction, a comprehensive and practical study of different kinds of tests appears in Nieto and Ruiz (2016). Finally, Menéndez and Hassani (2021) present several methodologies to achieve data augmentation in the tails of portfolio loss distributions to ensure robustness in ES estimations. They state that ES risk measure, as an FRTB benchmark, implies the renunciation of elliptic distributions for modelling the losses.
In turn, Laurent et al. (2016) analyse the theoretical foundations and implications of the default risk capital under the framework of the FRTB internal models, particularly in portfolios sensitive to credit risk. In Orgeldinger (2018), some recent advances are also presented to implement the FRTB regulation industrially under SA and IMA. The author defines implementation stages; analyses technological issues, unprecedented computational demands and associated costs; and highlights the need to reconcile SA with IMA models. In line with the above, Pederzoli and Torricelli (2021) estimate and compare FRTB impacts on the capital requirement under both approaches, SA and IMA, based on a stylised portfolio with different risk factors. They report a more significant impact on banks adopting SA. In turn, Porretta and Agnese (2021) examine FRTB impacts on capital the requirement for different banking groups, classified according to their tier-1 capital size. They analyse risk capital changes from the current to the revised regulation and for both approaches, SA and IMA.
However, under FRTB, logical reasonings should be put forward to support possible SbM implementations for a general portfolio. Logical reasonings respond to the requirement of building quantitative relations between SA-SbM and IMA-ES, as well as measuring risk capital impacts via SbM (Orgeldinger (2018) and Porretta and Agnese (2021)). Additionally,
metric's statistical performance and risk capital impacts should be investigated, particularly for financial options portfolios. Concerning the above literature, although data augmentation in Menéndez and Hassani (2021) is a viable way to obtain reliable ES measures, using periods of financial crises is essential for constructing stress scenarios under internal models.
Consequently, this article develops two proposals. First, it proposes an algorithm from the FRTB standardised approach to estimate the market risk capital relative to delta, vega and curvature risks through the sensitivities-based method. This systematic reasoning is related to and extends the work of Orgeldinger (2018) since the algorithm enables to foresee fundamental conditions for its implementation, such as the involved processes, its complexity and its high computational demand. In detail, for any portfolio, the algorithm allows us, according to the new regulation, to identify its risk factors and risk classes involved, estimate sensitivities and correlations between all the assets, perform risk aggregation and financial stress analyses, and calculate the overall risk capital. Also, it helps to analyse the interactions between the parts of the SbM scheme and experiment with hypothetical portfolios to measure impacts on risk capital. Furthermore, the algorithm is a design that can connect to desirable outcomes regarding risk capital levels or impacts, implying that it supports the creation of knowledge rules in the financial risk management field.
Second, to build communication bridges between the standardised and internal approaches under FRTB, a methodology is proposed to estimate the ES metric in a portfolio of financial options and evaluate its performance and the risk capital impacts. The robustness of our methodology is accomplished in three ways. First, it generates stress scenarios with periods of crisis, which feed loss distributions with extreme data; second, it adapts VaR and ES metrics to IMA; and third, it evaluates the metrics' performances via back-testing proofs. Risk capital impacts are studied by changing option tenors and liquidity horizons. At this point, the methodology constitutes a formal adaptation of ES to IMA for option portfolios. Furthermore, the proposed relationships between ES and FRTB are a step forward in the literature that can become a technical document annexe in BCBS (2019).
Subsequently, a numerical illustration is provided to promote an understanding of the sensitivities-based method and estimate a portfolio's specific impacts by following the proposed algorithm. Then, for supporting evidence of the validity of our methodology, an application is developed where the impact of ES and VaR under FRTB versus conventional VaR is measured in a simple portfolio of currency options. This development considers stress scenarios from the 2007-9 and 2020-1 crises and back-testing procedures.
The paper is organised as follows. Section 2 reviews the theoretical framework, and Section 3 defines the methodology. Subsequently, Section 4 addresses the results, and the most relevant findings are discussed in Section 5. The last section presents the conclusions and limitations of the work.
2. Literature review
2.1 Market risk measures
2.1.1 Value at risk, VaR. The monetary measure (in dollars) $VaR for a portfolio over a time
horizon and confidence level α satisfies the equation,
If the loss is assumed to be −ΠR, where Πis the initial value of the portfolio and R its return
over the time horizon, then equation is equivalent to
where VaR = VaR α = $VaR=Π and such risk measure is relative to the initial value of the
portfolio.
2.1.2 Expected shortfall, ES. The internal models approach in FRTB has chosen to follow the ES metric to quantify market risk. Conceptually and for simple computations, if −ΔΠ is the loss portfolio from Π in a given time horizon, then ES α is the conditional expectation of those losses that exceed VaR α in the loss distribution of −ΔΠ, where α is the confidence level of the risk measure.
More precisely, following Rockafellar and Uryasev (2002), let us consider that x∈X ⊂R n represents the vector of assignments in portfolio Π for a set of constraints X, and y ∈Y ⊂R m denotes the vector of future values of mmarket variables that affect the portfolio profit and loss. Then, the portfolio loss function can be represented as z = f (x; y). Moreover, if p(y) is the probability density of y over a time horizon T, then ESα for portfolio Π(x) at T is defined by
Alternatively, other expressions that define ESα in terms of the VaR measure appear in McNeil et al. (2005). Keeping their notation, these are given by
where L is an integrable function with continuous distribution that represents the portfolio losses, so that L = −ΔΠ, and the expression I A is the indicator function of event A.
Additionally, from the works of Rockafellar and Uryasev (2002) and McNeil et al. (2005), ESα can be obtained by appealing to the law of large numbers in terms of statistical orders so that
is a decreasing sequence of statistical orders for the losses fLjgm
and (.) the floor function applied in the argument.
2.2 Basel FRTB regulation
The following body of concepts and relations is taken from BIS (2019) .
2.2.1 IMA - ES
Now let us consider some features of IMA regarding the ES metric. The corresponding risk capital is estimated in stressed market conditions, using data over 12 months of stress, at a confidence level of 97.5%, and with a time horizon that varies depending on the liquidity of the risk variable or instrument under study.
The time horizons for liquidity are established as 10, 20, 40, 60 and 120 days. However, all calculations are based on changes in risk factors across overlapping 10-day periods, which is crucial since the samples produced are conceptually dependent.
Symbolically, if the risk factors are classified in bucket I according to the liquidity horizon LHi established in FRTB, then the market risk ES metric adjusted for liquidity is given by
where ES i represents the ES risk for the risk factors in buckets i; i + 1; … ; 5 by keeping the risk factors in buckets 1; 2;…; i −1 constant.
Next, to obtain the capital requirement, it is necessary to estimate the so-called weighted expected shortfall, WES, prescribed as
where EST is the ES measure of the entire portfolio and ESP j is the partial ES measure linked to the trading table j. Finally, the capital CR for market risk on day t is
where NMRF indicates the capital requirement of non-modellable risk factors.
The regulation agrees upon two performance tests (back-testing and profit and loss). The first must be carried out in the banking book, while both tests must be carried out in the trading book. Furthermore, in the trading book, the back-testing is based on the 1-day VaR
metric and at two confidence levels, 97.5% and 99%, which must be calibrated with actual market data from the previous 12 months.
2.2.2 SA - SbM
FRTB regulation in the standardised approach includes the sensitivities-based method, where the market risk capital is estimated through delta, vega and curvature risks for the portfolio risk factors. Calculating such capital involves various tasks in which risk classes are identified, and according to objective sensitivity, risk factors are grouped into buckets or categories. From here, the capital requirement (CR) is allocated by risk aggregation mechanisms within and between buckets, correlation stress analysis and well-defined criteria in each risk class.
Symbolically, using the same notation and formulation as that established in FRTB, if sk is the net sensitivity of the portfolio instruments for each risk factor k and the sensitivity sk is weighted by the weight RWk, then the weighted sensitivity sk, WSk, is given by WS k = RW ksk ; (11)
where ρkl is the correlation between WSk and WSl. Also, the aggregation for delta or vega risk among different buckets is calculated as
where Sx = 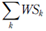 for all risk factors k in bucket x, and γbc is the correlation between buckets, provided the radicand is non-negative.
for all risk factors k in bucket x, and γbc is the correlation between buckets, provided the radicand is non-negative.
For other complementary formulations, as well as those related to estimations of capital requirement associated with curvature risk, see the regulation directly in BIS (2019) .
2.3 Back-testing in FRTB
A back-testing proof is a procedure, usually of a statistical nature, which evaluates the accuracy of a risk measure from historical data. The VaR measure is the metric agreed upon by FRTB regulation to be validated in a market risk management process. Specifically, these tests will be based on 1-day VaR, at 97.5% and 99% confidence levels, and calibrated with actual 12-month (250-day) market data.
2.3.1 Validation proofs. A set of eight statistical back-testing tests is referenced below to validate a VaR metric, classifying the tests according to whether they are frequency, independence or mixed.
(1) Frequency tests
Traffic light (TL), see BCBS (1996, 2006, 2011).
Binomial test (Bin), see an adaptation in Hull (2018).
Unconditional coverage test (UC), see Kupiec (1995).
Time until first failure (TUFF), see Kupiec (1995).
(2) Independence tests
Conditional coverage independence (CCI), see Christoffersen (2012, 1998).
Time between failures independence (TBFI), see Haas (2001).
(3) Mixed frequency and independence tests.
Conditional coverage mixed (CC), see Christoffersen (2012, 1998).
Time between failures mixed (TBF), see Haas (2001).
Method
3.1 FRTB standardised approach - sensitivities-based method
The different portfolio instruments in the trading book are related to risk factors and determine their price. In turn, risk factors are made to correspond to seven risk classes: interest rate (GIRR), three types of credit spread (CSR), equity (stock exchange), commodities and foreign exchange rate (FX).
Additionally, the different risk factors are grouped into buckets or categories in each risk class. For example, in the equity class, such buckets can be defined based on asset capitalisation and membership to a particular industry sector and a developed or emerging market. Buckets can also be specified according to a trading currency, the credit quality of an institution, the type of a commodity and the exchange rate between two currencies, among others.
Subsequently, SbM requires estimating three risk exposures via delta, vega and curvature for each factor. Regarding vega sensitivity, its risk-weighting considers the liquidity horizon of the respective risk class to which the factor belongs.
According to FRTB regulation, sensitivities must be aggregated under prescribed correlations, at bucket level and across buckets of the same class. Finally, the capital requirement CR of the initial portfolio is calculated for each of the seven risk classes and then added by a simple sum. The procedure is repeated in three correlation scenarios -low, medium and high- between the risk factors to consider correlation variations throughout the portfolio in periods of financial stress. The final capital requirement is the highest result obtained in the three scenarios.
Therefore, the logical structure of the processes involved in calculating capital requirements under the FRTB sensitivities-based method is complex. Next, we suggest Algorithm 1, which represents a preliminary version for a banking industry implementation of the SbM programme. The algorithm partly extends the work of Orgeldinger (2018) and is aligned with the need to automate modern standardised processes in market risk management from 2023. The implementation could also facilitate experimentation in calculating risk capital for hypothetical portfolios via FRTB SA SbM regulation.
The lines in Algorithm 1, except those containing loop processes, would lead to their own algorithms. The amount of “for” cycles reflects the entire process’s high complexity and computational demand. Comments in grey in lines 1, 2, 3 and 25 indicate specific items of the FRTB regulation to appeal to carry out the corresponding process. The remaining lines are the consequence of an integrated vision of Chapter MAR21 in FRTB.
Finally, lines 17, 19 and 25 involve, respectively, calculations for risk aggregation within and across buckets, and the establishment of capital requirement by scenario analysis according to correlations between buckets. Technical formulations were described and referenced in Section 2.2.2.
3.2 FRTB internal models approach - expected shortfall We propose an adaptation of the traditional historical simulation method to estimate the VaR and ES metrics for a financial option portfolio, consistent with FRTB ES conditions. In the first instance, an estimation of the historical VaR, satisfying FRTB conditions, is formulated for a portfolio of n financial options.
Definition 3.1. (Scenarios for option pricing). Consider a portfolio with initial value Π, composed by n financial options, where the asset underlying the i-th option is S i , i = 1; … ; n. Denote the price of option i on day j by fi;j; and suppose today is m day m. If we have m + N price observations for each option, it is possible to estimate feasible price scenariosf N i;j;m of the option on day m + N, defined so that the j-th scenario is
Proposition 3.1. (VaR-historical for option portfolio). Assume today is day m, a set of m price scenarios is generated for day m + N for each option i in a portfolio of n options, and the portfolio initial value is Π, where the scenarios are built according toequation (14)in definition 3.1, i = 1; … ; n. Then, the distribution of losses on day m þ N for the changes in −ΔΠ in N days is given by the following equiprobable loss space
where αi is the investment allocated to the i-th option. Thus, the monetary measure of the portfolio historical VaR at N days and at a α confidence level is estimated as the α percentile, Qα, of
, that is,
Proof. Without loss of generality, assume thatN ¼ 1. The truth of equation (15) is establishedby arguing according to the inductive method. Let P(k) be the given proposition for a portfolio with k options. The proposition is true for k = 1. Indeed, the loss p1 j of the portfolio on day m + 1, given the j-th scenario, is calculated as −α1 return, where return = f1j/ f1j−1−1. So
Now assume that P(k) is true. The conditional if P(k) then P(k + 1) is tautological since P(k + 1) = P(k) + P(1). Finally, from the definition of the VaR measure and equation (1), VaR α is the α percentile of {p 1 j } m j=1 . This ends the argument.
Remark 3.1. (VaR-normal and VaR-t). Alternatively, it is possible to fit a parametric distribution to the loss portfolio {p N j } m J=1 and thus obtain the corresponding VaR risk measures. VaR-normal and VaR-t are obtained by fitting a Gaussian distribution and a student-t with ν degrees of freedom distribution, respectively.
Second, an adaptation to the historical simulation method is proposed to estimate ES in a portfolio of n options consistently with FRTB specifications.
Proposition 3.2. (ES-historical for option portfolio). Starting from the same setting given in definition 3.1 and proposition 3.1, the ES α metric is approximated by
Proof. The estimation is achieved by appealing to equation (7), making the losses {L j;m } m j=1 equal to the losses {p N j } m j=1 established in equation (15) of proposition 3.1. In this way, whenm becomes large, ES α is approximated by equation (20).
Remark 3.2. (ES-normal and ES-t). Alternatively, it is possible to fit a parametric distribution to the loss portfolio {p N j } m j=1 and thus obtain the corresponding ES risk measures. ES-normal and ES-t are obtained by fitting a Gaussian distribution and a student-t with ν degrees of freedom distribution, respectively.
Remark 3.3. (ES and VaRrelationships with Basel FRTB). The above ES and VaRmetrics (historical, normal and t versions) are made compatible with the FRTB requirements when m = 250, α = 97:5%, the liquidity horizon in days is taken from N ∈{10; 20; 40; 60; 120} and the price scenarios f N i;j;m in equation (14) of definition 3.1 are obtained from m + N price observations in a stressed market. This way of proceeding is similar to FRTB prescriptions under IMA-ES.
Remark 3.4. (stress scenarios to consider in FRTB). The stress scenarios involved in definition 3.1 can be achieved from the 2007-9 global financial crisis and the 2020-1 pandemic crisis. The resulting measures, VaR and ES; adapted to FRTB, in addition to being related to portfolio risk capitals allow measuring and analysing impacts of both crises, providing trading book information for decision-making. In particular, because of the forthcoming market risk management regulation, any position in financial derivatives, either for hedging or investment purposes, should consider exposure levels through ES metrics under FRTB environments.
Results
4.1 Illustration: risk capital by the sensitivities-based method in Basel FRTB
BCBS documents in BCBS (2019) two simple examples to estimate capital requirements through the sensitivities-based method in the standardised approach, endeavouring to promote a level of understanding for its industrial implementation. However, the examples are remarkably brief and not very explicit in their calculations.
Therefore, this illustration looks to widen the scope of the example applied to an option position. To achieve this, the following procedure follows the steps of Algorithm 1 in Section 3.1, complements some estimations to be made in spreadsheets and explicitly indicates the FRTB articles to be used. These additional characteristics thus serve as an auxiliary guide towards studying and implementing the sensitivities-based method.
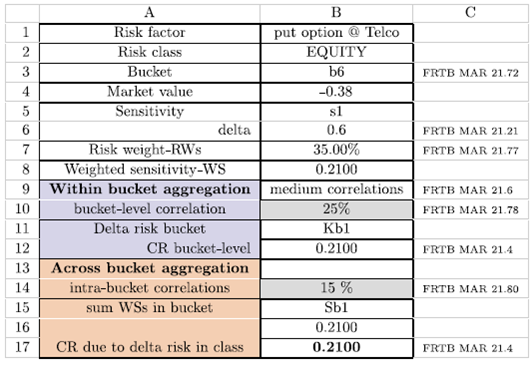
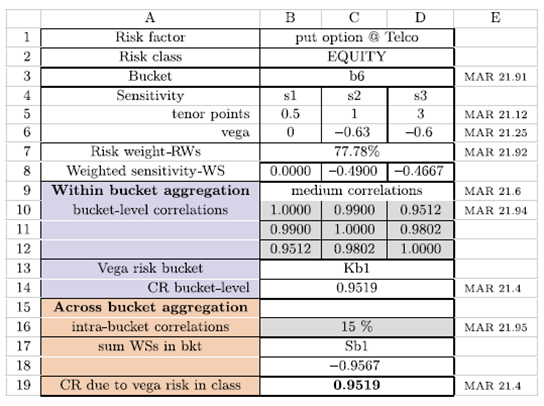
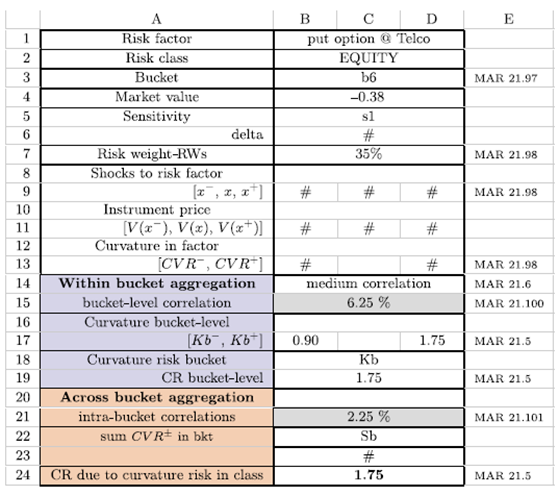
The banking portfolio in question consists of a short position put option on the hypothetical Telco asset, which reports in Canadian currency (CAD). Table 1 shows the essential data of the portfolio and reproduces Table A2.1 in BCBS (2019).
Consequently, Figures 1 2 -3 estimate the delta, vega and curvature risk capital in spreadsheets following the guidelines of Algorithm 1 under medium correlation scenarios. The notation used in the previous Tables was introduced in Section 2.2.2.
The right column of each spreadsheet references the specific FRTB items that support the calculations. When the calculations for delta and vega are repeated under low and high correlation scenarios, generating similar spreadsheets, delta risk capital remains at CAD 0.21, while vega capital increases to CAD 0.9567. As in BCBS (2019), it is assumed that the risk capital for curvature given the correlation stress is kept at CAD 1.75. In the worksheet represented in Figure 3, the calculations in the cells marked with # are ignored. However, the corresponding magnitudes are calculated as usual in derivatives valuation. The risk capital under the sensitivities-based method turns out to be CAD 2.9167. As a comparison, the results shown coincide with those reported in BCBS (2019) for vega and curvature risks in medium correlation scenarios. The remaining calculations shown in our study do not appear there.
To conclude, it is noted that total capital requirement is significantly greater than the option's value (by a factor of 7.6). Therefore, the bucket associated with the option is b6 (cell B3 in Figure 1), which means that the underlying asset, affiliated with the telecommunications sector, has a high capitalisation (≥ US$2tn, FRTB - MAR 21.74) and comes from an advanced economy (countries indicated in FRTB - MAR 21.75). From the above, it can be inferred that the risk capital of the option would be higher than that previously calculated for assets linked to low capitalisations or belonging to an emerging economy. Even though this illustration is hypothetical, it is based on an example with identical data built in BCBS (2019). Therefore, the described situation approximates possible impacts via SbM; in particular, the calculations show a high risk capital associated with SA. The estimations also reflect an effort to build relationships with IMA ES, consistent with the analysis proposed by Orgeldinger (2018) and Porretta and Agnese (2021). Also, the above implications for emerging economies' risk capital complement the studies of Majumder and Li (2018) and Valerio Roncagliolo and Villamonte Blas (2022).
The development of Algorithm 1 on a large scale would allow access to a platform to measure market risk and its possible impacts on a portfolio via the SbM schema. Such endeavour entails significant challenges regarding the instantiation of Algorithm 1. First, starting from a given portfolio, linguistic routines must be written to identify factors, buckets and risk classes. In addition, it is necessary to identify weighting factors and correlation matrices, generate sensitivities calibration routines from market data and create expert reports from text summaries. Finally, implementing each line within the algorithm loops should be processed in separate modules.
From a research point of view, analysing the algorithm's scope from computer science theories, like algorithm engineering, and evaluating its computational complexity using parallel processors, are open inquiries (see, e.g. Kliemann and Sanders (2016)).
4.2 Application: ES and VaR metrics under FRTB for a currency optionAportfolio composed of an at-the-money (ATM) European call option on GBP/USD having an annual maturity T ∈f0:5; 1g is considered. First, according to methodological section 3.2, VaR and ES option risks are estimated through an adaptation of the historical simulation method, consistent with the FRTB internal models approach. The estimations must be made by building stress scenarios for the underlying asset. Two reference frameworks are chosen for this: the 2007-9 global financial crisis and the 2020-1 COVID-19 pandemic crisis.
On the other hand, the estimated risk measures are compared with conventional VaR metrics via option Greek letters. The results allow evaluating of possible risk impacts on a GBP/USD call option and foreseeing which crisis scenario, 2007-9 or 2020-1, generates the most significant impact on capital.
Finally, according to Section 2.3, back-testing tests are executed for the VaR risk metrics conceived under FRTB versus traditional versions. The results suggest that the methodology proposed in Section 3.2 is reasonable.
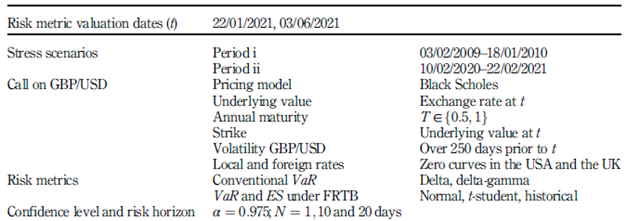
4.2.1 Market data and stress scenarios. In the following, dates are written in dd/mm/yyyy format. The data used correspond to the GBP/USD exchange rate and the treasury curves for the zero-coupon rate in the USA and the UK corresponding to the annual tenors T ¼ 0:5 and T = 1. The data are obtained from Bloomberg in the date range 01/03/2000 to 06/03/2021.
The periods of stress referred to in the risk metrics are the following:
(1) Period i: 2007-9 financial crisis. Date range considered: 02/03/2009-01/18/2010.
(2) Period ii: 2020-1 covid-19 crisis. Date range considered: 02/10/2020-02/22/2021.
4.2.2 Information for the estimation of VaR and ES. Table 2 summarises the information needed to measure the risk metrics in question. The valuation date t for VaR and ES metrics corresponds to any day between 02/22/2021 and 06/03/2021. In this case, two dates are chosen. Stress scenarios are periods i and ii previously described.
The estimated VaR and ES risk metrics are as follows. First, conventional delta and deltagamma VaR metrics are estimated as usual and independently of the stress scenarios. Second, calculations of VaR and ES in normal and t-student versions and adapted to FRTB are performed according to comments 3.1 and 3.2. Next, the adapted VaR and ES are obtained via historical simulation, as explained in Section 3.2, equations (16) and (20). Finally, the confidence level α and the horizon N of the risk metrics are established. According to FRTB, the α level is 0.975, and N depends on the liquidity of the asset underlying the financial instrument.
4.2.3 Risk metrics, comparisons and impacts. To begin with, the following notation is
established:
VaR, conventional view: VaR delta and delta-gamma metrics: VaR δ and VaR δγ.
VaR FRTB: VaR normal, t-student and historical metrics: VaR N, VaR T ν, VaR H. ν represents the degrees of freedom for the t-student distribution.
ES FRTB: ES normal, t-student and historical metrics: ES N, ES T ν , ES H.
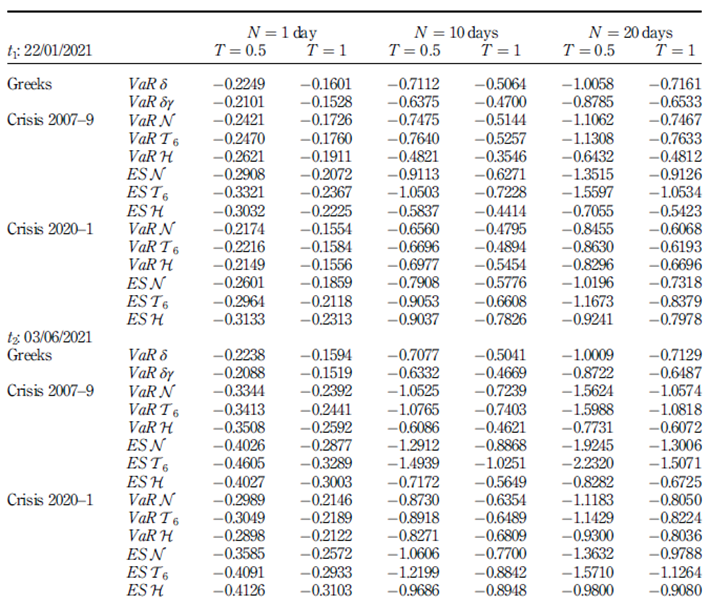
Subsequently, with the information given in Table 2 and the methodology defined in Section 3.2, the agreed risk metrics are estimated in relative terms as shown in Table 3, where risk metrics are computed traditionally for each date t via Greek letters and using 2007-9 and 2020-1 crisis stress scenarios via FRTB. The table also considers three possible horizons N and two possible maturities T of the option.
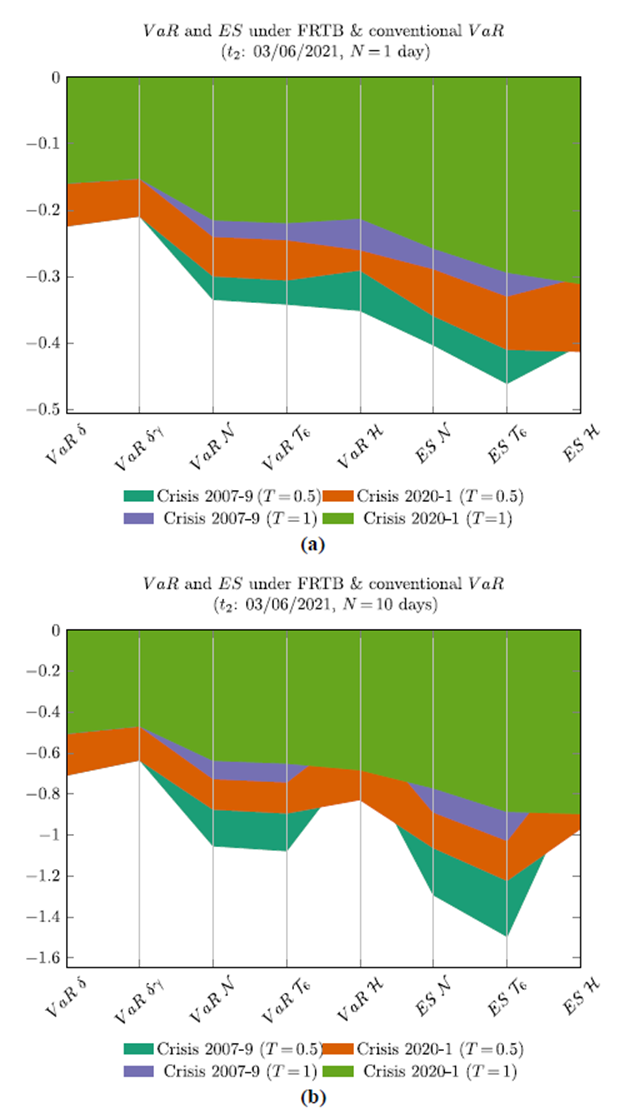
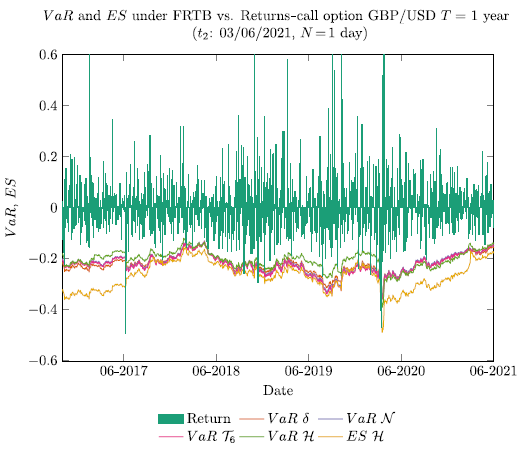
For comparison purposes, the results in Table 3 can be represented in area diagrams according to the pair (t;N). For example, the results corresponding to pairs (t 2 ; 1) and (t 2 ; 10) are illustrated in Figure 4.
Table 3 VaR and ES at N days under FRTB and traditional VaR
Note(s): Call option on GBP/USD
Source(s): Own elaboration
The following approximate pattern is observed in Table 3.
Expiration T: VaR and ES risk metrics are higher for the call options with the lowest maturity (T = 0:5 years).
VaR, conventional view: VaR δ and VaR δγ are independent of the stress scenarios posed.
VaR FRTB: In both crisis periods, 2007-9 and 2020-1, VaRH≲ VaRN ≈ VaR T 6 . Read the relation ≲ as “less than or approximate to”. Therefore, historical VaR would lead to a lower risk capital compared to the normal and t-student versions.
VaR: Regarding the 2020-1 crisis, conventional VaR measures are ≲ the historical VaR measure. Thus, the risk capital generated by VaR H via FRTB is approximate to or greater than the corresponding one using the conventional counterparts, VaR δ and δγ.
Crisis stress scenarios - FRTB: The 2020-1 crisis has a more significant impact on the historical VaRand ES measures, while the 2007-9 crisis has it on the normal and t-student measures of VaR and ES. The calculations related to ES show an alternative view to those developed by Menendez and Hassani (2021). While the former considers stress scenarios under financial crises in the loss portfolio, the latter is based on synthetic data augmentation methodologies. Back-testing in FRTB can help analyse ES performance and therefore validate whether the alternatives respond satisfactorily to the regulation.
VaR and ES - FRTB: In each crisis period, ES measures are > than the respective VaR measures. In the 2007-9 crisis, ES increases compared to VaR are 22% in the normal
model, 38% in the t-student model and 15% in the historical model. Regarding the 2020-1 crisis, these figures correspond to 21%, 36% and 21%, respectively. Horizon N: At a higher horizon N, only VaR H and ES H metrics are limited by the restriction that the potential loss cannot exceed 100% of the portfolio value. Additionally the data suggest it is inaccurate to use the factor √N p to estimate the risk at N days from the risk at one day. This last fact is aligned with the analysis and evidence found in Danıelsson and Zigrand (2006) and Pederzoli and Torricelli (2021).
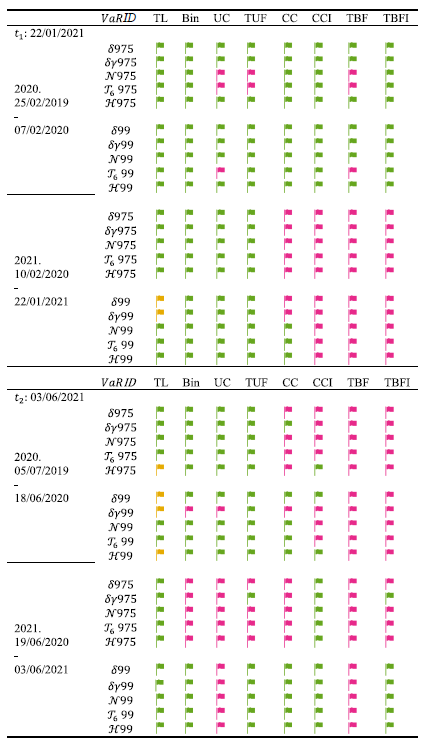
4.2.4 Back-testing. Figure 5 shows call option returns vs VaR and ES measures under FRTB and VaR under the Greek delta, where the dynamic behaviour of the risk measures can be observed. To evaluate the performance of VaR metrics, Table 4 reports eight back-testing tests given by TL, Bin, UC, TUF, CC, CCI, TBF and TBFI, described in Section 2.3. VaR metrics via Greek letters are VaR δ and VaR δγ, and those via FRTB are VaRN, VaR T 6 and VaR H. Computationally, all the risk metrics are estimated through a script in Matlab.
Table 4 Back-testing on different VaR metrics: FRTB and conventional frameworks
Note(s): Call option on GBP/USD
Source(s): Own elaboration
In the first column of Table 4, there are two valuation dates denoted by t = t1 and t = t2 for which the tests are to be carried out (dates are the same as in Table 3). These tests are executed over two successive periods of 250 days before t. The second column identifies the names of the VaR measures considered. The number 975 or 99 is added to the respective names, depending on the risk metric’s confidence level, 97.5% or 99%. Finally, the flag symbols in the remaining columns indicate the test result. The green colour means that the test is accepted, that is, the respective null hypothesis of the test is not rejected at a significance level of 5%. Meanwhile, red indicates that the test is rejected, and yellow indicates the warning zone established in the TL test.
The overall performance of all risk measures under back-testing is good. However, we believe that comparatively the performance of the historical VaR metric under FRTB is preferable. First, VaRH975 and VaRH99 are shown to be satisfactory measurements under frequency and independence tests, while VaR H99 turns out to be reasonable under mixed proofs. Second, the metric in question passes a higher number of back-testing procedures, which is reflected in a higher number of assigned green flags.
In sum, the previous observations and the results reported in Section 4.2.3 suggest that historical ES and VaR metrics under FRTB are reasonable for risk management of the call option considered under the internal models’ approach. The metrics in question were defined in equations (16) and (20) of Section 3.2.
Severity validation tests for VaR metrics, as in Colletaz et al. (2013), and back-testing procedures for ES, as in Kratz et al. (2018) and Deng and Qiu (2021), are part of current research agendas. Finally, extending our analysis towards emerging economies, as in Serrano Bautista and Nuñez Mora (2021), is a future agenda.
5. Discussion
This work develops two proposals for market risk estimations and their associated impacts under FRTB regulation, which comes into effect in 2023. First, it proposes an algorithm to estimate risk capital via the SA-SbM framework. An illustration of a hypothetical position in options shows a possible implementation of the algorithm in spreadsheets to evaluate impacts, yielding that the risk capital to position value ratio for an advanced economy is 7.6. Second, we design a methodology to assess ES in options portfolios via IMA. An application is then developed to investigate the impact of ES and VaR under FRTB versus conventional VaR on GBP/USD call options, considering the 2007-9 and 2020-1 crises for building stress scenarios. It is found that historical VaR leads to lower risk capital and performs better by back-testing procedures than the normal and t-student versions. Also, the 2020-1 crisis had a significant impact on historical VaR and ES, while the 2007-9 crisis on the normal and t-student VaR and ES counterparts. In turn, historical VaR and ES are bounded by 100% of the portfolio value. Furthermore, the data suggest that extrapolating the risk to N days by magnifying the risk to 1 day by the factor √N is inaccurate.
The above illustration of the algorithm suggests that, for emerging economies, the risk capital to position value ratio would be more drastic than previously indicated. Financial institutions must join efforts or restructure their portfolios to meet SA SBM requirements. On the other hand, the proposed methodology for evaluating ES risk via IMA has shown reliability to be incorporated in a risk management programme or even be considered as a technical document annexe in FRTB.
Implementing the two proposals can become a technological tool for the banking industry or an experimentation platform to explore possible marginal impacts concerning SbM or ES under FRTB. Regarding IMA-NMRF, a whole field of exploration of new uncertainty-based theories opens since the subjective aspect of this component has not been dealt with in previous Basel regulations. Further research should evaluate the impacts of the new regulation on more complex portfolios than those examined in this study. Finally, computational complexity issues must be considered for the implementation of the algorithm.
6. Conclusions
With the new Basel FRTB regulation for market risk in 2023, banking institutions must prepare for future impacts and complex challenges in knowledge management, technological and human resources implementation, ethical and accounting frameworks, portfolio restructuring and institutional capital. The two proposals presented in this work draw communication bridges between the sensitivities-based method in the standardised approach (SA-SbM) and the expected shortfall in the internal models approach (IMA-ES).
The proposals aim to provide methodologies whose implementations assist in measuring market risk and the associated impacts on risk capital. The bridges seek to analyse the impacts of risk capital in different economies and make the associated risk capitals more convergent and comparable. All the above will support decision-making processes concerning risk-based capital requirements and strengthen institutional risk management processes.
Our research shows that under the SA-SbM schema and from a stylised option portfolio, the risk capital to position value ratio is higher than 7 and would impact emerging economies. Also, under the IMA-ES framework and from a currency options portfolio, we present evidence that the methodology defined for measuring market risk is satisfactory, considering FRTB requirements and a statistical point of view.
The technical and managerial complexity levels involved in the Basel FRTB regulation are today a focus of attention for institutions and academics. This work focuses on the FRTB-SA-SbM and FRTB-IMA-ES components of the FRTB regulation for market risk in options. The effects of SA-DRC, SA-RRAO, IMA-NMRF and IMA-DRC components remain to be measured.