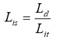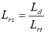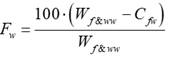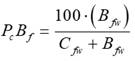1. Introduction
1.1. Influence of Artificial Intelligence on the design of an agave leaf shredder
From the end of the 19th century to the beginning of the 20th century, shredding machines have been developed, and the mechanical properties of fibers have been determined (Mendoza & Mendoza, 2017; Hidalgo-Reyes et al., 2015). Yet, these machines have been designed and constructed to shred leaves of species other than Agave angustifolia Haw., particularly those of greater economic interest such as Agave sisalana and Agave fourcoides (Murali & Morchhale, 2014; Kumar et al., 2022). The process of shredding A. angustifolia leaves is a task that is carried out traditionally using the so-called enriado method (Campaña et al., 2020). Despite advances in the construction of agave leaf shredder prototypes, the cutting elements design parameters to carry out the shredding continue to be established empirically and are usually based on previous prototypes (Pérez del Río et al., 2013). Selecting optimal parameters for the design of a leaf shredder regarding its structure and functioning (Leal-Iga et al., 2021) is a difficult task that could improve if new artificial intelligence technologies are implemented. Genetic Algorithms (GAs) are adaptable search algorithms that depend on evolutionary algorithms, which generate high-quality solutions for complex engineering and optimization problems (Aydin et al., 2020). GAs are often used as research tools in scientific model processes, providing accurate identification and formulation of the objective function (Mirjalili, 2019). The formulation, discussion and generalization of GAs for multi-objective optimization were described according to Na et al. (2013), where a rank-based fitness assignment method for Multiple Objective Genetic Algorithms (MOGAs) is used for placement and adjusting the tenant data. The main advantage of MOGAs is their versatile ability to add different constraints and objectives. It also allows the user to choose between a set of solutions, all with the same level of acceptance for the GAs but with different properties that enable them to decide which one to select according to the system of interest requirements (Suksonghong et al., 2014). Quaglio et al. (2020) suggest using analytical and experimental models for the optimization of design parameters; but, it is very complicated to deal with on some occasions since determining the optimal design parameter values can need a large number of material resources and considerable calculations and analysis, as well as time for experimentation, for two reasons: 1) the number of combinations can be very high, and 2) the objective function cannot usually be obtained as a function of the input parameters. Artificial Neural Networks (ANNs) currently allow for modeling and solving complex problems with greater ease and less expense in a shorter time (Li et al., 2020).
1.2. Artificial Intelligence applied in Engineering
A machinery design problem should have two main elements: the number of characteristics or mechanical components and the precision of the process to be performed. Although many design optimization problems involve complex tasks and lack information to resolve them, thus, a «pragmatic» approach is required in the search for the best or better solutions. In this regard, using evolutionary meta-heuristic algorithms that imitate the mechanisms of evolution in nature could be implemented, which have been used to solve multi-objective optimization problems and have been applied to engineering practice (Liu et al., 2021). Previous studies show that Artificial Intelligence has yielded satisfactory results in various engineering applications. This research proposes a hybrid method, combining a Neural Network as an objective function, capable of modeling the relationship of design variables with product quality parameters, in this case, fiber, and a GA that optimizes those variables. This combination has been used in the engineering field with very satisfactory results; for example, in the construction sector, as in Vajdian et al. (2020) where the shear capacity of panel zone in steel columns is determined, and the authors demonstrated that the optimization algorithm is robust through the output function. Similarly, Feng & Li (2013) applied a back-propagation network model incorporating GAs that was more efficient and accurate in the estimation of construction costs than only the back-propagation network model. In Ehsani & Dalir (2019) they optimized the design process of an angle grid structure using ANN and GA, where the trained ANN was used to achieve a precise and effective approximation of the buckling load. Sebaaly et al. (2018) used a combination of GA and neural networks to automate an asphalt mix design process with the ability to predict and optimize its constituents, subject to a couple of constraints, to get the desired mix properties and provide its durability without making laboratory tests. ANNs and GAs can be used as simulation and optimization tools in other engineering areas. So, in Boutemedjet et al. (2019) the wing planform parameters of a mini unmanned aerial vehicle (UAV) were determined through an optimization hybrid method to perform the aerodynamic design procedure for aerial reconnaissance at low altitude and low Reynolds number. In Vishwanathan (2019) a design of a multicylinder internal combustion engine crankshaft was developed by optimizing four design parameters to accommodate the wear and tear of the crankshaft due to the gearing action and so convert the engine unnecessary/extra torque into vehicle speed. In the same way, a numerical study for test crash worthiness capability of designed multi-cell structures was conducted through a technique of combined neural networks and genetic algorithm ANNs-GA (Pirmohammad & Esmaeili Marzdashti, 2018), to optimize cross-sectional shapes used to absorb impact energy, where the objective functions were obtained from the constructed neural networks to find the non-linear equations of crash worthiness indicators regarding the design variables. Also, the main parameters of the energy absorption behavior of steel thin-walled structures with rectangular cross-sections, under the quasi-static loading, were modeled using an ANN and a response surface method, also with these numerical data a systematic crash worthiness study was carried out with a multi-objective optimization design using GA (Dadrasi et al., 2020). Optimization of composite angle grid plates under different loads shows that ANNs and GAs reduce computational costs with great accuracy and can help to choose the maximum buckling load at the minimum structural weight (Ehsani & Dalir, 2019). In Wang et al. (2021), through a hybrid model, combining GA and ANNs, the authors confirm the relationship between the laser-induced welding parameters (fusion width, energy density, laser-arc coupling point and welding penetration) and the welding joints geometry to determine the energy transfer and track in real-time the process quality. As in Khezri et al. (2020), ANNs and GAs are considered among the most modern tools used to estimate and maximize the wax production rate in a Steady-State Gas-to-Liquids (GTL) Plant.
Although there are different optimization methods such as Bio-inspired Algorithms or Differential Evolution Algorithms included in Evolutionary Algorithms, which are efficient in solving different optimal control issues present in various engineering areas (Annisa et al., 2018), the main aim of this research was to develop a hybrid model based on an artificial neural network and a genetic algorithm that allows establishing the relationship between the shredding process quality and the optimal design parameters selection of an Agave angustifolia Haw leaf shredder, through numerical methods, based on technological power, hardware, as well as the versatility of the calculation, software. According to the above, the machine's constructive features will be modeled using these innovative design tools through the hybrid algorithm. This will allow a combination of experimental and numerical computing methods to solve an optimization problem that was previously complicated.
2. Materials and methods
The material used in these experiments was fifty Agave angustifolia Haw. leaves, which were collected manually and selected completely at random in an agave crop with an average age of 8 years. Then, their length, width, thickness and weight were measured.
The dimensions that characterize the leaf were measured; length was determined using a 5M Milwaukee magnetic tape measure (No. 48-22-7716); thickness was determined with a 300 mm Mitutoyo digital calibrator (No. 500-193) with 0.01 mm accuracy; leaf mass was determined using a Vinson Vins-20 grain-scale with a maximum capacity of 20 kg and 0.001 kg accuracy. Besides, to determine the feed rate of the leaves into the machine, their input and output times were measured using a digital stopwatch with 0.01 s accuracy.
To cut the spine from the leave tip, Barrilito (12”) stainless steel scissors were used. Finally, a mark was drawn on the leaf to state the cutting length (1 m) using a Sharpie black permanent marker.
2.1 Leaf characteristics
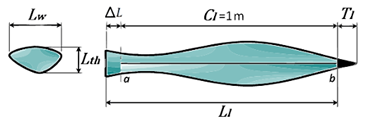
Figure 1 shows the schematic of an Agave angustifolia Haw. leaf, depicting the variables that characterize them by their dimensions, where, T l is the length of the spine at the leaf tip, which is dark brown and flattened above the base (Economía, 2005), L l is the length of leaves, L w is width of leaves, L w is leaf width, which varies by becoming greater in the center of the leaf’s length, L th is leaf thickness, which is the distance from the lower surface or back side to the upper surface; it also varies by becoming smaller from the base of the leaf to the spine, C l is the cutting length, ∆L is an extra length for the grip, which for safety reasons this part will not be shredded.
The agave leaves are linear, rigid, straight, ascending, green, or glucose green to yellowish green, with almost straight margins. Before the tests, due to the above characteristics, the product should be cut longitudinally to uniformize the samples in size and shape, to then measure their mass.
2.2 Shredding test
A test bench was designed and built to shred the agave leaves. First, the dimensions of the shredder component were defined according to Pérez del Río et al. (2013) (Figure 2), where, S dd is the shredder drum diameter, and S dl is the drum length, which coincides with the length of the blades to cover the entire L w , i.e., S dl =B l .
An angular profile with dimensions of 0.0381 x 0.0381 x 0.0635 m was used to support the shredder blades. As an energy source, a 5.6 kW (7.5 HP) electric motor with a rotation frequency ω=1765 rev/min was selected. The feed roller diameter (R d ) to meet the leave grip condition was 0.115 m. The number of blades in the shredder cylinder was Z=16 to maximize the number of cuts to the leaf due to the rotation movement (Figure 2a), which was established through previous trials that consisted of increasing 𝜔 for a blade edge tangential speed (T s ) until the entire leaf cortex was detached.
To establish the study variables, the mechanical process of shredding agave leaves was analyzed in three main stages (Figure 2b). Firstly, there is a partial cut by shearing of the leaf; in this cut, the distance between the blades and the counter-blade, called shredding clearance (S c ), must be greater than the fibers’ thickness to avoid cutting them; but it must not exceed a small range of this thickness to prevent soft material particles from remaining without detaching. The partial leaf shearing is due to the cutting forces in the initial cut stage; these are oriented in the same direction as the counter-cutting elements and the opposite direction. But then, because of the shredder’s circular movement, they are located tangentially to it, allowing the fiber´s accommodation in the space belonging to S c and thus avoiding total shearing.
Another essential geometric parameter is S h ; the shredding height expressed as the vertical distance from the counter-blade to the shredder cylinder center.
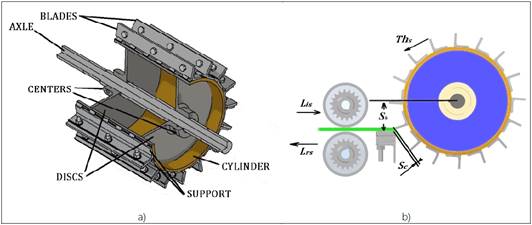
Figure 2. Schematic of the agave leaf shredder: a) Shredder elements. b) Physical variables of the shredding process.
Secondly, the total detachment of the soft material occurs, caused by the thrust of the inner part of the blade´s edge. This process requires a thrust speed (Th s ) to completely detach the soft material particles from the fibers. If the minimum speed is not reached, the soft material particles will move along with the fibers to the interior of the machine. And thirdly, there is a soft material thrusting caused by the inertia of its weight adhered to the blades. During the second and third stages, a friction process occurs between the blade´s edge and the fibers. In principle, this happens when the leaf input speed (L is ) to the shredder is very low and occurs when the leaf recoil speed (L rs ) is very low; in both cases, the fibers undergo excessive blade action, which causes their deterioration and rupture (Pérez del Río et al., 2013).
Under the above considerations, the S c , L is , and L rs values were taken as design variables; these last two were calculated as follows (Equation 1 and2):
where, L d is the shredded leaf length, L it is the leaf input time to the shredder element, L rt is the leaf recoil time from the shredder element.
The S c adjustment was made with a thickness gauge, placed between the blade and the counter-blade. After shredding, the fibers were cut and the grip weight of half of the shredded leaf was determined; this grip corresponds to the part near the base that was not shredded and was used to thrust the leaves inside the machine and then remove them.
Besides, the weight of the whole fibers (W fw ) together with the waste material that remains adhered was determined, as well as the weight of the broken fibers. Later, the fibers were sun-dried for 48 hours to determine the weight of the dried entire fibers, and the waste, as well as the weight of the mechanically cleaned dry fibers.
The percentage of fiber waste (F w ) is given by the percentage ratio indicated in Equation (3), while the percentage weight of the broken fibers (P c B f ) relative to the total weight of the broken fibers plus the clean fibers is given by Equation (4):
where W f &ww is the weight of entire fibers and waste, C fw is the weight of clean fibers, B fw is the weight of broken fibers. In the shredding process, 0% damaged fibers and 0 % waste would be ideal. But these variables are inversely proportional, i.e., as one increases, the other decreases, and vice versa (Pérez del Río et al., 2013).
Below is the shredding process quality classification according to the fiber waste percentage.
When there is a waste excess, the fibers come out with a continuous part of non-fibrous material that prevents separation. As a result, it is impossible to see a considerable number of threads, and the process quality is poor.
For a medium amount of waste, the shredding process quality is medium and almost acceptable when there are some areas where the fibers continue to be attached to the fibrous leaf part.
For an acceptable amount of fiber waste, the quality is good when some particles of non-fibrous material are observed. Still, the fibers are independent and ready to be processed and used.
2.3 Shredding process modeling with Neural Networks
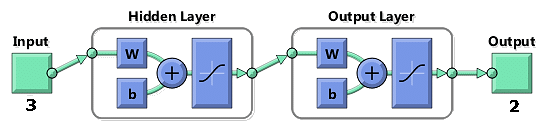
To optimize the shredder’s design parameters, a neural network was developed using the Neural Network Toolbox included in MATLAB software, choosing a feed-forward back propagation neural network using the newff command (Figure 3):
net=newff(E,O,[10,5],’tansig’, ’purelin’, ’trainlm’,’learngdm’,’mse’).
The number of neurons in the neural network input layer was defined by the number of design parameters, which were adjusted to different values during the tests; these were three: shredding clearance, leaf input speed, and leaf output speed. The output variables were the quality parameters of the shredding process (the percentages of fiber waste and broken fibers); i.e., two neurons in the output layer element.
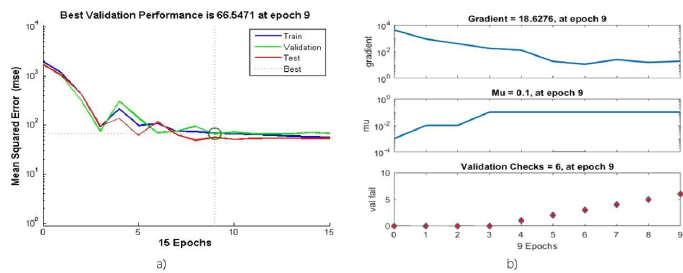
For the hidden input and output layers, training was carried out for different combinations. The network was programmed with a hyperbolic tangent sigmoid transfer function for the input, while a linear transfer was used for the output. The Levenberg-Marquardt backpropagation, a network formation function that updates weight and bias according to Levenberg-Marquardt optimization, was used for network training. The weight and trend learning function used was gradient descent. The root means squared error (RMSE) was used to measure network performance and show algorithm consistency.
2.4 Approximation of the model to experimental values
Using a linear regression, it is proposed to contrast and analyze the model implemented with the experimental data of training, validation and testing.
2.5 Application of Genetic Algorithms to solve multi-objective optimization
Based on the problem complexity, an optimization method was implemented through GA to search for the weight of the artificial neural network. The optimization carried out by Neural Network Toolbox in MATLAB through GA, gamultiobj (objFcn, nvars) finds the points in the Pareto front of the objective function that in this case is the neural network, objFcn=@(E)sim(net,E’) and nvars is the dimension of the optimization problem (number of decision variables). That is, it minimizes the percentage values of fiber waste and the percentage of broken fibers.
Constraints to the problem are given by the limits of the experimental variables; where S c was constricted as (1.2< S c <2.0) mm, input speed as (0.4< I s <0.6) m/s and output speed as (0.6 < O s < 1.0) m/s.
Linear inequality constraints are left in the form A=[-1 0 0; 1 0 0 ; 0 -1 0; 0 1 0; 0 0 -1; 0 0 1]. The values for this inequality would be as follows: b=[-1.25; 2; -0.4; 0.6; 0.5; 0.8]; both linear inequality constraints, a lower and a higher limit of the solution, are left without values because the problem has no such constraints.
3. Results and discussion
3.1 Leaf characteristics
The main dimensions of agave leaf samples (Figure 1) are presented below, where T l fluctuated between 15 and 20 mm, L l had a length between 1.1 and 1.3 m, an approximate L w of 80 to 100 mm, and an average moisture of 79.5 %. Besides, C l was set at 1 m from the leaf tip, after trimming the spine, which was maintained with ∆L.
Then, the agave leaf was divided in half along the fiber to avoid its concave shape in the cross-section, because given their stiffness, it does not settle on the counter-blade and makes shredding difficult. Finally, the leaf portions were weighed before shredding.
3.2 Shredding test
The main dimensions of the shredder to perform the test were S dd =0.370 m and S dl =0.285 m. Also, the S c values considered for the experiment were 1.25, 1.3, 1.5, 1.6 and 2 mm, and the minimum 𝜔 was 1500 rev/min, for T s =27.175 m/s. Too, S h was set at 0.028 m, obtaining a distance from the shredding section of 0.00020439 m.
For the proposed experiments, the variation in L is presented a greater influence on the length of a blade’s action than the variation in 𝜔.
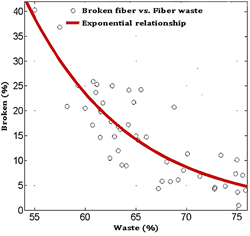
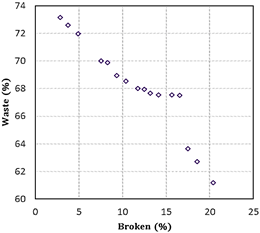
Figure 4 shows the relationship between the variables that define shredding quality, considering Pérez del Río et al. (2013) as a comparative reference, indicating that increased fiber cleanliness leads to an increase in the percentage of broken fibers.
According to the experimental results, for a shredding distance of 0.0013 m, 37 % cleanliness was obtained; thus, the expected percentage of whole fibers will be 78 % with 95 % reliability (Figure 5a).
For the percentage of broken fibers (Figure 5b), there was an excess when the number of broken fibers was greater compared to the entire fibers, from a third to about half. Besides, the excess of broken fibers ended up hindering the shredding process by accumulating at the time of removing the leaf; this percentage was medium when there were several broken fibers that did not hinder the shredding process. But it was a significant loss that could affect yield at the process´ end. This parameter was acceptable when only fibers that had structural anomalies or those that had a lower resistance to the adhesion strength of the non-fibrous material on them, and it was inevitable that they would break.
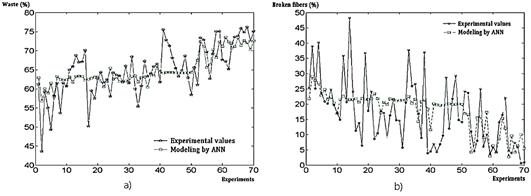
Figure 5. Behavior of the experimental shredding process about modeling: a) Waste. b) Broken fibers.
Table 1. Estimates of the shredding process quality
| Classification | Waste (%) | Broken fibers (%) |
| Poor | 70-75 | 30-40 |
| Medium | 65-75 | 20-30 |
| Good | 55-65 | 20-0 |
From the above, the influence of S c , L is , and L rs is visible as the machine design parameters that constitute independent variables, since their variation has a direct influence on shredding quality. In this case, shredding quality would be the dependent variable and this, in turn, is defined by the percentage of whole fibers; this depends on the relationship between the weight of the clean whole fibers and the weight of the broken fibers.
3.3 Shredding process modeling with Neural Networks
Several data percentage combinations were used for neural network training validation, where the best values were obtained for 70/100, i.e., 70 %, 15 % to compare the input values with the output ones, and 15 % to verify the network effectiveness.
net.divideParam.trainRatio =70/100; % Adjust as desired
net.divideParam.valRatio = 15/100; % Adjust as desired
net.divideParam.testRatio = 15/100; % Adjust as desired
In the hidden input layer, training was carried out with 5 to 15 neurons, obtaining better results for 10, while in the hidden output 3 to 10 were used, and a better result was also obtained with 10 neurons.
During this procedure, the best value of RMSE = 0.099 was obtained at nine training epochs (Appendix Aa and Ab), likewise, Kaveh & Chayjan (2014) and Zarein & Jaliliantabar (2014) obtained similar statistical results when implementing this method in the prediction of the dehydrated properties of Pistacia atlantica L. and white mulberry.
3.4 Approximation of the model to experimental values
With the linear regressions, it was possible to check the model reliability on the experiments, obtaining in total a regression coefficient of more than 0.96; this will allow determining the leaf shredder characteristic design parameters.
3.5 Application of Genetic Algorithms to solve multi-objective optimization
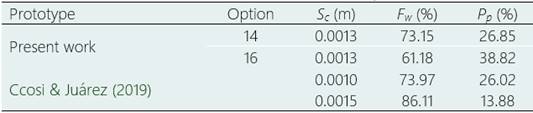
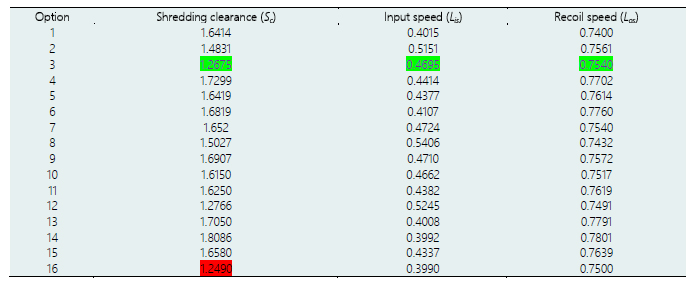
Figure 6 corresponds to possible design solutions of the elements studied, generated with the Pareto front during multi-objective optimization, where both the broken fiber and fiber waste criteria were minimized. The optimum point corresponds to option 14 which presented the lowest number of broken fibers (2.83 %) and at the same time the highest amount of waste (73.15 %), so, the number 16 has the lowest percentage of fiber waste with 61.18 % but the highest percentage of broken fibers (20.38 %). Also, all values were selected by shredding quality criteria (Appendix B).
According to the machine adjustments, in variable 14 a product performance, P p , of 26.85 % was obtained, a value slightly higher than Ccosi & Juárez (2019) who report P p =26.02 % for the shredding of pineapple leaves in a similar machine. In this regard, Table 2 shows a comparison of the performance between the optimization of the shredding process applied to this study with respect to Ccosi & Juárez (2019), highlighting that to a greater amount of fiber waste the product performance decreases, thus showing the direct dependence of F w on P p , without relying on S c .
In Table 3 a comparison is shown indicating the main parameters that influence the shredding process of the Agave Angustifolia Haw leaves, where the machine’s productivity is quite high, so its use is very indispensable. The fiber cleaning was greater by the manual process, yet, in relation to F w , both the manual and mechanical-optimized processes are similar. When shredding the leaves with the mechanical-un optimized process, there is a low depulping efficiency, increasing to 90% with the modifications made. The fiber obtained through the mechanical-optimized process decreases the damage caused by the blades, as these only slipped without reaching to cut them.
With regard to the mechanical properties of fibers, the resistance to the tension and the elasticity module reported by García et al. (2020) using the machining process was greater than Silva et al. (2009) with the manual method. With the optimization of the equipment, a higher quality fiber was obtained because the pulping percentage increased. Also, the optimized machine does not deteriorate the environment because the amount of water used was less than with the manual process. The work capacity of the shredder meets the needs of the producer, which would allow increasing its fiber production.
Table 3. Comparison of shredding processes
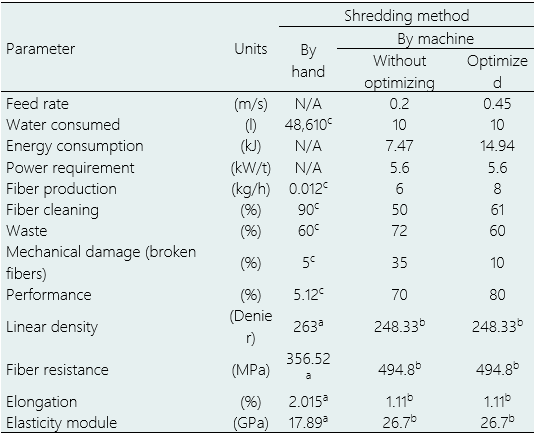
N/A: Does not apply Silva et al. (2009) a, García et al. (2020) b, López (2008) c.
Regarding the costs of the machine, Table 4 mentions the main items that make up its value, after optimizing the process, indicating an increase in the investment of 19.84% about the prototype price without optimizing, stressing that, in exchange for this price, improvements in the performance and quality of processed fiber would be obtained.
Table 4. Cost of the Agave shredder
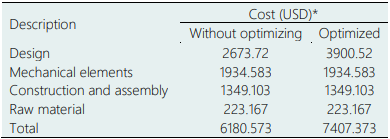
*Values calculated by Mayorga (2004), updated to 2022, considering inflation of 110% according to INEGI between 2004-2022.
In general terms, hybrid models have an acceptable level of reliability because they integrate the development of ANNs with GAs for the optimization of various engineering problems that present a high level of complexity regarding their solution, as in Khezri et al. (2020) who through using ANNs and GAs report the development of a hybrid model of the Steady-State GTL process to estimate the wax production rate, then implemented in an optimization problem to maximize the solution of the GTL parameters that improves the wax production and reduces the time of calculations. So, Han et al. (2021) implemented this combination to design an appearance plan for developing industrial products, taking as an example the shape of a set of drones, where the hybrid model presented a very high accuracy allowing to test this plan in a better way, both practical and mathematically, compared to traditional methods. Other optimization cases were applied in the work of Pirmohammad & Esmaeili Marzdashti (2018), in multicellular structure tubes, with five different cross-sectional shapes, used to select an energy absorbing device with the best crash worthiness capability, where it was found that octagonal multi-cell structure presented a better resistance on other test variants. Similarly, in Wang et al. (2021) a prediction model to describe the morphology of laser induced TIG hybrid welding joints by using the BP neural network optimized through the GA was established; in this case, the results showed that the estimated values were quite accurate relative to the actual profile of the welding joint, because the mean absolute percentage error of each group of data presented a good fit.
4. Conclusions
A hybrid model that involves artificial intelligence, based on a neural network and a genetic algorithm, was developed to establish the relationship between the best shredding process and the optimal design parameters selection of an Agave angustifolia Haw leaf shredder using numerical methods. The machine’s constructive characteristics were modeled using innovative design tools through the hybrid algorithm mentioned, which could be capable of addressing the design problems of agricultural machine elements. Multi-objective optimization using genetic algorithms proved to be a practical way to achieve an optimal design solution in the face of a complex problem exacerbated by a lack of information. The study of the problems in the selection of multi-objective operating characteristics of agricultural machinery is an important issue that should be addressed in future research work.