Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Comuni@cción
versión impresa ISSN 2219-7168
Comuni@cción vol.9 no.1 Puno ene./jun. 2018
Método cuatro pasos y el aprendizaje de la derivada por definición
Method four steps and the learning of the derivative by definition
Melecio Paragua Morales1, Lorenzo Pasquel Loarte2, Carlos Alberto Paragua Macuri3, Melissa Gabriela Paragua Macuri4, Tomasa Verónica Cajas Bravo5
1 Universidad Nacional Hermilio Valdizán Perú. E-mail: melecioparagua@unheval.edu.pe
1 Universidad Nacional Hermilio Valdizán Perú. E-mail: lorenzo_pasquel_loarte@hotmail.com
1 Centre national d’études spatiales (CNES). E-mail: carlos.paragua@pucp.edu.pe
1 Universidad Nacional Mayor de San Marcos. E-mail: melissa.paragua@unmsm.edu.pe
1 Universidad Nacional Hermilio Valdizán Perú. E-mail: verónica-cajas@hotmail.com
RESUMEN
El presente artículo tiene como objetivo probar que la aplicación del método cuatro pasos, mejora el aprendizaje de la derivada por definición en estudiantes de la escuela profesional de Matemática y Física de la universidad nacional Hermilio Valdizán (UNHEVAL); donde se tiene como objetivos específicos: comparar, analizar y evaluar el nivel de aprendizaje de la derivada por definición con la aplicación del método cuatro pasos. El tipo de investigación es explicativa y diseño cuasi experimental con grupo experimental y grupo de control. La población-muestra de estudio es 105 estudiantes de ambos sexos, cuya composición es para el grupo de control = 35 y grupo experimental 70 estudiantes respectivamente; los resultados descriptivos iniciales tienen cierta semejanza en ambos grupos, las diferencias empiezan a mostrarse durante la prueba de proceso, y más aún luego de la prueba final en favor del grupo experimental, quienes recibieron el benefició de la aplicación del método cuatro pasos. Los estadígrafos de la estadística descriptiva e inferencial permiten obtener el resultado siguiente: el valor Z de Prueba = 10,44 se ubica a la derecha de z crítica = 1,96; que es la zona de rechazo, por lo tanto, se rechaza la hipótesis nula y se acepta la hipótesis alternativa; es decir, se tiene indicios suficientes que prueban que el nivel de aprendizaje de la derivada por definición mejoran con la aplicación del método cuatro pasos, en los estudiantes de ambos sexos, de la escuela profesional de matemática y física.
Palabras clave: Método cuatro pasos, Derivada por definición, Aprendizaje de la derivada por definición.
ABSTRACT
The objective of this article is to prove that the application of the four-step method improves the learning of the derivative by definition in students of the professional school of Mathematics and Physics of national university Hermilio Valdizan (UNHEVAL); where it has as specific objectives: compare, analyze and evaluate the level of learning of the derivative by definition with the application of the four-step method. The type of research is explanatory and quasi-experimental design with experimental group and control group. The population-study sample is 105 students of both sexes, whose composition is for the control group = 35 and experimental group 70 students respectively; The initial descriptive results have certain similarity in both groups, the differences begin to show during the process test, and even more after the final test in favor of the experimental group who received the benefit of the application of the four-step method. The statisticians of the descriptive and inferential statistics allow to obtain the following result: the Z value of Test = 10.44 is located to the right of z critical = 1.96; which is the rejection zone, therefore, the null hypothesis is rejected and the alternative hypothesis is accepted; that is, there is sufficient evidence to prove that the level of learning of the derivative by definition improve with the application of the method four steps, in students of both sexes, the professional school of mathematics and physics.
Keywords: Four-step method, Derived by definition, Derivative learning by definition.
I. INTRODUCCIÓN
El análisis matemático es una asignatura base en la escuela profesional de matemática y física, sin embargo, no es de la preferencia de los estudiantes de ambos sexos próximos a ser docentes en esta especialidad, como consecuencia, tienen dificultades en el aprendizaje de los diferentes tópicos de la asignatura; es por ello que en la investigación se propuso la aplicación del método cuatro pasos y con ello mejorar el nivel de aprendizaje de la derivada por definición, en los estudiantes de ambos sexos de la escuela profesional de matemática y física en la Universidad Nacional Hermilio Valdizan.
Como antecedentes se ha considerado aquellas investigaciones que proponen la aplicación de un estilo de aprendizaje para resolver el problema detectado, entre ellas se tienen: Paragua (2015), se propuso aplicar el criterio de la primera y segunda derivada para mejorar el nivel de aprendizaje de la gráfica de funciones; para ello, desarrolló una investigación de tipo explicativo, con un diseño cuasi experimental; además, del análisis descriptivo de los datos, aplicó una prueba de hipótesis de la diferencia de dos medias, donde el valor Z de Prueba = 7,09 se ubicó a la derecha de z crítica = 1,96; por lo tanto, rechazó la hipótesis nula y aceptó la hipótesis de investigación, porque había indicios suficientes que prueban que el uso del criterio de la primera y segunda derivada como método mejoró el nivel de aprendizaje de la gráfica de funciones en los estudiantes de ambos.
En esta misma tendencia, (Paragua 2014 y Paragua 2008), ante otros problemas de aprendizaje estudiados, aplicó diferentes estrategias de aprendizaje con la finalidad de solucionar los problemas estudiados; también Paredes (1995), desarrolló la tesis: "Aplicación interactiva por descubrimiento de los usos de recursos y materiales didácticos en educación secundaria, estudió de los casos de dos centros", de tipo explicativo y diseño cuasi experimental, mide el grado de efectividad de los recursos y materiales didácticos en cada clase, y concluye: Que el uso de recursos y materiales didácticos en cada clase de manera sistemática y con mucha pertinencia son muy beneficiosos para el aprendizaje de los alumnos. Propone que el profesor debe usar los recursos y materiales didácticos en cada clase de manera sistemática y con mucha pertinencia, dicha aplicación debe ser de manera interactiva y por descubrimiento.
En esta misma línea de investigación, (Rodríguez 2008, Viviano 2008, Albino 2001, Copari 2014 y otros), encontraron que la problemática de los alumnos radica en sus niveles de aprendizaje de la matemática; éstos, no son los óptimos; es por ello que el propósito de los investigadores es buscar estrategias de aprendizaje para revertir la problemática descritas.
Coherente con los antecedentes citados, el propósito de la investigación es probar que la aplicación del método cuatro pasos mejora el nivel de aprendizaje de la derivada por definición en los estudiantes de ambos sexos de la escuela profesional de matemática y física de la UNHEVAL; para lo cual, los propósitos específicos son determinar: el nivel de saberes previos respecto a la derivada por definición; el nivel de aprendizaje de la derivada por definición durante el proceso de aplicación del método cuatro pasos; el nivel de aprendizaje de la derivada por definición al finalizar el proceso de aplicación del método cuatro pasos; además, comparar, analizar y evaluar: el nivel de aprendizaje de la derivada por definición antes y después del proceso de aplicación del método cuatro pasos; y, el nivel de aprendizaje de la derivada por definición con, y sin la aplicación del método cuatro pasos utilizando la definición de derivada.
En el artículo se reporta la solución de un problema latente en los estudiantes de ambos sexos: se refuerza primero el aprendizaje mecánico y repetitivo, hasta una toma de conciencia plena, para ello se procurar la contextualización de los problemas de tal forma que permita a los estudiantes buscar una aplicación práctica de la teoría en la solución de los problemas de la vida diaria.
1.1. Teorías básicas y aplicaciones
Los estudiantes de ambos sexos de la escuela de matemática y física de la UNHEVAL inician sus estudios sobre derivadas sin tener claro los conceptos básicos de funciones, y el límite de una función. En este sentido ƒ' (x), representa a la derivada de la función ƒ en un punto de la nueva función ƒ', en el cual dicha función es derivable; además, la derivada de una función es 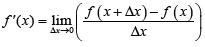 , límite con el que se calcula la derivada de una función por definición; sin embargo, las dificultades didácticas están vinculadas con el rechazo operacional que permite el paso al límite, la noción de función y continuidad, así como los obstáculos geométricos, lógicos y simbólicos (Sierpinska, 1994).
, límite con el que se calcula la derivada de una función por definición; sin embargo, las dificultades didácticas están vinculadas con el rechazo operacional que permite el paso al límite, la noción de función y continuidad, así como los obstáculos geométricos, lógicos y simbólicos (Sierpinska, 1994).
Los estudiantes llegan a dominar de manera mecánica los aspectos algorítmicos, por repetición en abundancia de ejercicios (Neira, 2013); sin embargo, no llegan a contextualizar sus aprendizajes, el mismo que no les permite comprender, por ejemplo que la primera derivada de una función es una nueva función susceptible de otra derivación, esta ocurrencia sucede porque durante el proceso de resolución de la derivada por definición, pierde de vista la parte conceptual y por ello dan mayor importancia al proceso algebraico de la derivación.
En este sentido, Cantoral (2000) y Azcárate (2000), atribuyen a la débil existencia de saberes previos de las unidades de análisis, casi en todas las investigaciones observadas el resultado de la prueba de entrada es en promedio no más de diez, en la escala vigesimal, es decir, el diagnóstico de los saberes previos de los estudiantes de ambos sexos es máximo 50%, ello no les permite anclar de manera eficiente los nuevos conceptos de tal forma que se conviertan en significativos, es decir, disponibles, evocables, consistentes en el tiempo, (Ausubel 1983).
En el proceso del método cuatro pasos para derivar, h es el incremento en el eje, de manera indistinta se trabaja con h o su equivalente; hecha la aclaración y con la finalidad de que el cálculo de la derivada por definición se facilite, tal como sugiere Tan (2000): (1) "Se calcula ƒ(x+h). (2) Se formula y calcula la diferencia ƒ(x+h)-ƒ(x). (3) Se formula y calcula el cociente 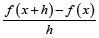 . (4) Se reemplaza y calcula
. (4) Se reemplaza y calcula 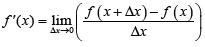
La aplicación práctica en base a la sugerencia de Tan (2000) para derivar funciones lineales son:
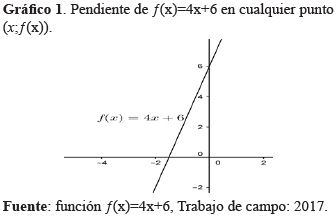
Ejemplo N° 1: Halla la pendiente de la recta tangente a la gráfica de en cualquier punto (x;ƒ(x))
La pendiente de la recta tangente en cualquier punto sobre la gráfica de ƒ está dada por la derivada de dicha función en x. El ejemplo es una función lineal, entonces la recta tangente en cualquier punto debe coincidir con la propia recta, esa es la razón para que tenga la misma pendiente que la recta, y como se observa en la función la pendiente es 4.
La aplicación práctica en base a la sugerencia de Tan (2000) para derivar funciones cuadráticas son:
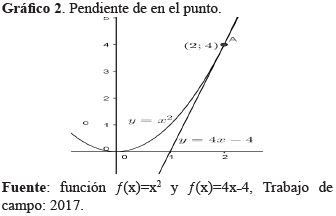
Ejemplo N° 2: Halla la pendiente de la recta tangente a la gráfica de ƒ(x)=x2 en un punto específico para: ƒ'(2).
En la ecuación y = mx + b → y = 4(2) b → b= -4 de esa forma se halla la ecuación y = 4x-4.
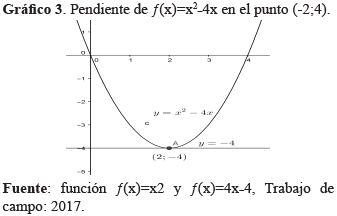
Ejemplo N° 3. A partir de ƒ(x)=x2-4xcalcula ƒ'(x). Halla el punto sobre la gráfica de ƒ donde la recta tangente a la curva es horizontal y grafica ambos. ¿Cuál es la razón de cambio de ƒ en este punto?
El punto donde la recta tangente es horizontal es en ƒ'(x)=0, operando 2x – 4 = 0 → x = 2, luego el valor está dado por y=ƒ(2)=₋4, entonces el punto de tangencia horizontal es (2);-4; como la pendiente de la función es positiva y la gráfica abre hacia arriba, entonces el punto hallado es el más bajo, denominado Punto Mínimo. La razón de cambio de ƒ en x=2 es cero (0).
La aplicación práctica en base a la sugerencia de Tan (2000) para derivar funciones de grado > 2 son:
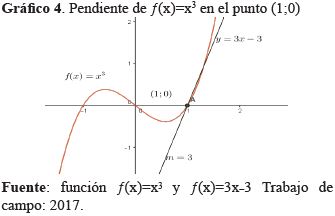
Ejemplo N° 4: A partir de x3. Calcula ƒ'(x). Halla la pendiente de la recta tangente T a la gráfica de ƒ en el punto donde x=1. Escriba la ecuación de la recta tangente T.
La pendiente de la recta tangente T a la gráfica de f cuando x=1 está dada por ƒ'(1)=3.
De otro lado, si x=1→y=ƒ(1)=(1)3=1, entonces T es tangente a la gráfica de ƒ en el punto (1; 0).
La pendiente de T es, entonces la ecuación de T es: y₋0=3(x₋0) reemplazando y operando se tiene y=3x₋3
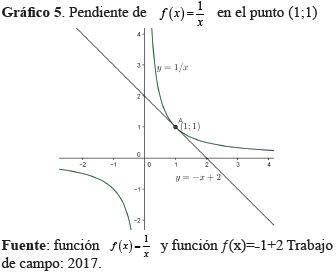
Ejemplo N° 5: A partir de. Calculaƒ'(x). Halla la pendiente de la recta tangente T a la gráfica de 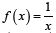 en el punto donde x=1 Escriba la ecuación de la recta tangente T
en el punto donde x=1 Escriba la ecuación de la recta tangente T
Se aplica el método cuatro pasos:
La pendiente de la recta tangente T a la gráfica de ƒ cuando x = 1 está dada por ƒ'(1)=₋1.
De otro lado, si x=1→y=ƒ(1)=1, entonces T es tangente a la gráfica de ƒ en el punto (1;1).
La pendiente de T es -1, entonces la ecuación T es: y-1=1(x-1) reemplazando valores se tiene y=-x+2.
II. METODOLOGÍA
El tipo de investigación es Explicativo, Hernández (2006), Paragua (2014); el diseño es cuasi experimental, Paragua y Otros (2008), Paragua (2012); el esquema del diseño es el siguiente:
GE: O1-------x------O2------x------O3
GC: O1--------------O2--------------O3
Leyenda: GE = grupo experimental; GC = grupo de control; On = Observaciones; x = variable independiente.
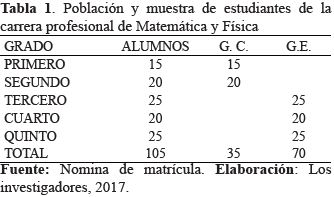
La población – muestra estaba constituido por los 105 estudiantes de ambos sexos de la escuela profesional de matemática y física, el tipo de muestreo aplicado es el no aleatorio (Pacori, 2014), debido al número de estudiantes no ameritaba un muestreo probabilístico.
El instrumento de recolección de datos fue la prueba escrita, con la denominación de prueba de entrada (PE) que permite diagnosticar el nivel de saberes previos; prueba de proceso (PP) con el que se mide el nivel de aprendizaje a la mitad de la aplicación del método cuatro pasos; y prueba final (PF) que permite medir el nivel de aprendizaje al finalizar el proceso de investigación. Cada uno con 10 preguntas, calificado con 2 puntos por pregunta que permite el uso de la escala de 0 a 20 puntos.
Las pruebas fueron validadas por menor variabilidad, los datos para ello se obtuvieron a partir de pruebas piloto hasta por tres momentos.
Para el análisis de los datos procesados se usó la estadística descriptiva en los análisis descriptivos en función a las medidas de tendencia central y de dispersión; el desplazamiento del primero hacia la derecha es lo que indica la mejora en los niveles de aprendizaje, y la disminución del segundo indica la homogenización del nivel de aprendizaje de la derivada por definición; también se hizo uso de la estadística inferencial en la prueba de hipótesis para la diferencia de dos medias, con la distribución normal z.
El estudio se ubica en el paradigma positivista, en ese sentido, se manipulan las variables aplicando la variable independiente: método cuatro pasos, esperando que los niveles de aprendizaje de la derivada por definición mejoren en las unidades de análisis.
III. RESULTADOS
Durante el trabajo de campo de la investigación se aplicó como estrategia de aprendizaje el método cuatro pasos para mejorar el nivel de aprendizaje de las unidades de análisis en la derivada por definición; sin embargo, al inicio se les diagnosticó el nivel de saberes previos, (Mota y Valles, 2015), (López, 2009) sobre temas como: polinomios, operaciones con polinomios, funciones, tópicos de geometría plana y geometría analítica, que poseían las unidades de análisis; los bajos saberes previos motivó dos sesiones de retroalimentación; luego de ello se aplicó la variable independiente durante todas las sesiones programadas, y se observó a la mitad y al finalizar el trabajo de campo cuyos resultados del grupo experimental se presentan en la siguiente tabla.
En la tabla se observa que las medidas de tendencia central van en aumento, ello quiere decir que el nivel de aprendizaje de la derivada por definición mejoran a partir de los saberes previos, durante el proceso hasta el final de la aplicación del método cuatro pasos; también las medidas de dispersión, a partir de la prueba de proceso disminuye indicando una homogenización de dichos aprendizajes; de otro lado, el coeficiente de asimetría pasa de positivo a negativo configurando una asimetría negativa.
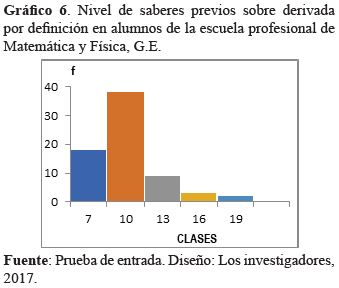
En el gráfico que antecede se observa que el nivel de saberes previos respecto a la derivada por definición de los estudiantes de ambos sexos estaban por debajo de diez de nota en la escala de calificación de 0 a 20, con una fuerte tendencia hacia Xmín. = 5, configurando una asimetría positiva; es decir, el mayor apuntamiento con tendencia hacia la izquierda.
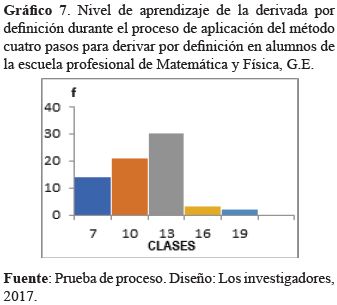
En el gráfico que antecede se observa que los niveles de aprendizaje de la derivada por definición mejoraron durante el proceso de aplicación del método cuatro pasos, porque el mayor apuntamiento se ha trasladado a la clase 13, confirmándose el segundo objetivo específico de la investigación; sin embargo, aún está configurando una asimetría positiva.
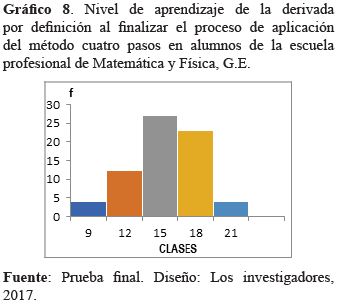
En el gráfico se observa que el mayor apuntamiento se ha desplazado a la clase 15, respecto a la prueba de proceso y configura una asimetría negativa, quiere decir que los niveles de aprendizaje de la derivada por definición mejoran de manera significativa al finalizar la aplicación del método cuatro pasos.
Se hizo una comparación entre el nivel de saberes previos y el nivel de aprendizaje final en el grupo experimental con la aplicación del método cuatro pasos, y se comprobó que mejoraron los niveles de aprendizaje de la derivada por definición en 5,28 puntos en promedio.
De la misma manera, al final del estudio se hizo una comparación cruzada entre el grupo experimental y el grupo de control, el resultado fue que la aplicación del método cuatro pasos mejoraron el nivel de aprendizaje del cálculo de la derivada en 5,23 puntos en promedio, respecto a las unidades de análisis donde no se aplicó la variable independiente.
Los datos para la prueba de hipótesis se obtuvieron a partir de los análisis descriptivos, tanto del grupo experimental como del grupo de control y son los siguientes: Media (GE) = 14,37; Media (GC) = 9,14; Varianza (GE) = 7,22; Varianza (GC) = 5,18; n (GE) = 70; n (GC) = 35; 95% de confiabilidad; E = 5% como nivel de significancia, con cola a la derecha; y, z = 1,96 para 95% de confiabilidad. Ello permitió la siguiente formulación de hipótesis: H0:µE≤µC y HA:µE>µC.
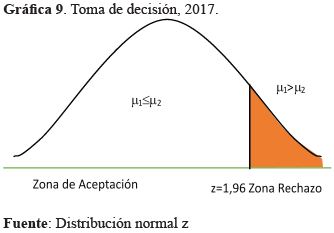
La hipótesis alterna indica que la prueba es unilateral de cola a la derecha, porque se trata de verificar sólo una probabilidad; y se usó la distribución normal z.
El valor de la Z de prueba, se calcula con la fórmula: 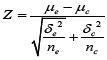 reemplazando los valores se tiene:
reemplazando los valores se tiene: 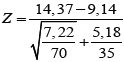 luego Z = 10,44
luego Z = 10,44
El valor de prueba Z = 10,44 en el gráfico que antecede, se ubica a la derecha del valor crítico z = 1,96; es decir, en la zona de rechazo, por lo tanto, se rechaza la hipótesis nula y se acepta la hipótesis alterna; es decir se tiene indicios suficientes que prueban que el nivel de aprendizaje de la derivada por definición mejora con la aplicación del método cuatro pasos, en los estudiantes de ambos.
IV. CONCLUSIONES
Los saberes previos sobre la derivada por definición y el método cuatro pasos de las unidades de análisis; se ubicaron en la clase regular de la escala, como no era lo óptimo, se les retroalimentó en los temas previos de tal forma que al momento de aplicarles el método cuatro pasos, no tuvieran dificultades mayores en el aprendizaje de la derivada por definición.
Los resultados comparativos muestran mejores niveles de aprendizaje de la derivada por definición en los estudiantes de ambos sexos que se beneficiaron con la aplicación del método cuatro pasos, en comparación con las unidades de análisis del grupo de control.
La prueba de hipótesis indica que sí tiene indicios suficientes que muestran que el nivel de aprendizaje de la derivada por definición mejora con la aplicación del método cuatro pasos en los estudiantes de ambos sexos de la escuela profesional de matemática y física de la Universidad Nacional Hermilio Valdizán.
CONFLICTO DE INTERESES
Los autores declaramos no tener conflicto de intereses.
AGRADECIMIENTO
A la Universidad Nacional Hermilio Valdizán por financiar la investigación a través de FEDU y a los estudiantes de la Escuela Profesional de Matemática y Física por su participación en la experiencia de aplicación del método cuatro pasos.
REFERENCIAS BIBLIOGRÁFICAS
Albino, J. y otros. (2001). El método interactivo y el aprendizaje de la matemática en el tercer grado del C.N. de Aplicación, UNHEVAL – 2001. Tesis. UNHEVAL. Huánuco. Perú.
Azcárate, C. (2000). El precálculo, un eslabón necesario entre las funciones y el análisis. Las matemáticas del siglo XX, una mirada en 101 artículos. 259 – 262. Recuperado de: http://www.sinewton.org/numeros/numeros/43-44/Articulo52.pdf [ Links ]
Ausubel, D. (1983). Psicología Educativa y la Labor Docente. Disponible en: http://www.utemvirtual.cl/plataforma/aulavirtual/assets/asigid_745/contenidos_arc/39247_david_ausubel.pdf Consultado el 16-10-2016 [ Links ]
Cantoral, R. y otros. (2000). Sobre el estatus de la noción de derivada: De la epistemología de Joseph Louis LaGrange al diseño de una situación didáctica. Revista Latinoamericana de Investigación en Matemática Educativa. Vol. 3, número 003, 255 – 292. Disponible en Web: http://www.clame.org.mx/relime/200002c.pdf [ Links ]
Copari, F. G. (2014). La enseñanza virtual en el aprendizaje de los estudiantes del Instituto Superior Tecnológico Pedro Vilcapaza – Perú. Comuni@cción: Revista de Investigación en Comunicación y Desarrollo, V. 5, N. 1, ENE-JUN, 2014. pp. 14 -21 [ Links ]
Flores, R. y otros. (2008). Fundamentos del Cálculo. Editorial GARABATOS. ISBN: 970-9920-18-5 Consultado el: 11-08-2016. Disponible en: http://www.mat.uson.mx/sitio/documentos/fundamentos-de-calculo.pdf [ Links ]
Hernández, R. y otros. (2006). Metodología de la Investigación. Edit. McGraw. Hill. Colombia. [ Links ]
López, J. A. 2009. La importancia de los conocimientos previos para el aprendizaje de nuevos contenidos. ISSN: 1988-6047. [ Links ]
Mota, D. J. y Valles, R. E. (2015). Papel de los conocimientos previos en el aprendizaje de la matemática universitaria. ISNN on-line: 2178-5201. Doi: 10.4025/actascieduc.v37i1.21040 [ Links ]
Neira, G. 2013). Dificultades detectadas al pasar del álgebra al cálculo en educación matemática. Revista Infancias Imágenes / pp. 44-50 / Vol. 12 N° 1 / enero – junio 2013.
Paragua, M. (2014). Investigación Científica. Educación Ambiental con Análisis Estadístico. Editorial Académica Española. OmniScriptum GmbH & Co. KG. [ Links ]
Paragua, M. (2012). Investigación Científica Aplicada a la Educación Ambiental con Análisis Estadístico. Editorial: Sociedad Geográfica de Lima. Primera Edición. Ibegraf. Lima. [ Links ]
Paragua, M., Macuri, C, y Rojas, R. (2008). Investigación Educativa. JTP Editores E.I.R.L. Huánuco. Perú [ Links ].
Paredes, J. (1995). Aplicación interactiva por descubrimiento de los usos de recursos y materiales didácticos en Educación secundaria estudio de los casos de dos centros. Tesis. Universidad Complutense. Madrid. España.
Pozsgai, E. (2014). Diseño de tareas que contribuyan a un aprendizaje significativo del concepto de derivada en estudiantes de Ciencias Administrativas. Tesis. PUCP. Lima. Perú.
Sierpinska, A. (1994). Comprensión en Matemáticas. Estudios en la serie de educación matemática. Londres: The Falmer Press. [ Links ]
Skemp, R. (1989). Relating theories to practice in the teaching of mathematics. Disponible en: https://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot2005a-cerme4_poynter_tall.pdf Consultado el: 16-10-2016. [ Links ]
Tan, S. (2000). Matemáticas para Administración y Economía. Editorial Thomson – Learning. Segunda edición. México D. F. [ Links ]
Viviano, A. (2008). El Ludotrix y el aprendizaje de la Matemática. Tesis. UNHEVAL. Huánuco. Perú.
Recibido el: 26/12/2017
Aceptado el: 08/03/2018